Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-10T21:51:16.376Z Has data issue: false hasContentIssue false
  • English
  • Français

L-functions of GL2n: p-adic properties and non-vanishing of twists

Part of: Discontinuous groups and automorphic forms Algebraic number theory: local and $p$-adic fields

Published online by Cambridge University Press:  08 January 2021

Mladen Dimitrov ,
Fabian Januszewski  and
A. Raghuram
Mladen Dimitrov
Affiliation:
Laboratoire Paul Painlevé, CNRS, UMR 8524, University of Lille, 59000Lille, Francemladen.dimitrov@univ-lille.fr
Fabian Januszewski
Affiliation:
Institut für Mathematik, EIM, Paderborn University, Warburger Str. 100, 33098Paderborn, Germanyfabian.januszewski@math.upb.de
A. Raghuram
Affiliation:
Indian Institute of Science Education and Research, Dr. Homi Bhabha Road, Pashan, Pune411021, Indiaraghuram@iiserpune.ac.in
Get access Rights & Permissions [Opens in a new window]

Abstract

The principal aim of this article is to attach and study 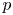$p$-adic 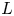$L$-functions to cohomological cuspidal automorphic representations 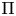$\Pi$ of 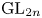$\operatorname {GL}_{2n}$ over a totally real field 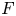$F$ admitting a Shalika model. We use a modular symbol approach, along the global lines of the work of Ash and Ginzburg, but our results are more definitive because we draw heavily upon the methods used in the recent and separate works of all three authors. By construction, our 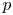$p$-adic 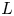$L$-functions are distributions on the Galois group of the maximal abelian extension of 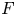$F$ unramified outside 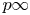$p\infty$. Moreover, we work under a weaker Panchishkine-type condition on 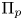$\Pi _p$ rather than the full ordinariness condition. Finally, we prove the so-called Manin relations between the 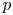$p$-adic 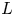$L$-functions at all critical points. This has the striking consequence that, given a unitary 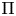$\Pi$ whose standard 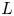$L$-function admits at least two critical points, and given a prime 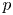$p$ such that 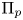$\Pi _p$ is ordinary, the central critical value 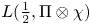$L(\frac {1}{2}, \Pi \otimes \chi )$ is non-zero for all except finitely many Dirichlet characters 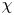$\chi$ of 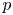$p$-power conductor.

Keywords

p-adic L-functionsnon-vanishing of L-functionsautomorphic forms on GL(2n)

MSC classification

Primary: 11F67: Special values of automorphic $L$-series, periods of modular forms, cohomology, modular symbols
Secondary: 11S40: Zeta functions and $L$-functions 11F55: Other groups and their modular and automorphic forms (several variables) 11F70: Representation-theoretic methods; automorphic representations over local and global fields
Type
Research Article
Information
Compositio Mathematica , Volume 156 , Issue 12 , December 2020 , pp. 2437 - 2468
Check for updates
Copyright
© The Author(s) 2021

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Asgari, M. and Shahidi, F., Image of functoriality for general spin groups, Manuscripta Math. 144 (2014), 609–638.CrossRefGoogle Scholar
Ash, A., Non-square-integrable cohomology classes of arithmetic groups, Duke Math. J. 47 (1980), 435–449.CrossRefGoogle Scholar
Ash, A. and Ginzburg, D., p-adic L-functions for $GL(2n)$, Invent. Math. 116 (1994), 27–73.CrossRefGoogle Scholar
Barrera, D., Dimitrov, M. and Jorza, A., $p$-adic $L$-functions of Hilbert cusp forms and the trivial zero conjecture, J. Eur. Math. Soc., to appear.Google Scholar
Barthel, L. and Ramakrishnan, D., A non-vanishing result for twists of $L$-functions for $GL(n)$, Duke Math. J. 74 (1994), 681–700.CrossRefGoogle Scholar
Chen, F. and Sun, B., Uniqueness of twisted linear periods and twisted Shalika periods, Sci. China Math. 63 (2020), 1–22.CrossRefGoogle Scholar
Chinta, G., Friedberg, S. and Hoffstein, J., Asymptotics for sums of twisted L-functions and applications. In Automorphic representations, L-functions and applications: progress and prospects, Ohio State University Mathematical Research Institute Publications, vol. 11 (de Gruyter, Berlin, 2005), 75–94.CrossRefGoogle Scholar
Clozel, L., Motifs et formes automorphes: applications du principe de fonctorialité. In Automorphic forms, Shimura varieties, and $L$-functions, Vol. I, Perspectives in Mathematics, vol. 10 (Academic Press, Boston, MA, 1990), 77–159.Google Scholar
Dimitrov, M., Automorphic symbols, $p$-adic $L$-functions and ordinary cohomology of Hilbert modular varieties, Amer. J. Math. 135 (2013), 1–39.CrossRefGoogle Scholar
Eischen, E., Applications of nonarchimedean developments to archimedean nonvanishing results for twisted L-functions, Math. Res. Lett., to appear.Google Scholar
Friedberg, S. and Jacquet, H., Linear periods, J. Reine Angew. Math. 443 (1993), 91–139.Google Scholar
Gan, W. T. and Raghuram, A., Arithmeticity for periods of automorphic forms. In Automorphic representations and $L$-functions, Tata Institute of Fundamental Research Studies Mathematics 22 (Tata Institute of Fundamental Research, Mumbai, 2013), 187–229.Google Scholar
Gehrmann, L., Shalika models and $p$-adic $L$-functions, Israel J. Math. 226 (2018), 237–294.CrossRefGoogle Scholar
Grobner, H. and Raghuram, A., On the arithmetic of Shalika models and the critical values of $L$-functions for $\operatorname {GL}_{2n}$, Amer. J. Math. 136 (2014), 675–728.CrossRefGoogle Scholar
Hida, H., Control theorems of $p$-nearly ordinary cohomology groups for $\operatorname {SL}(n)$, Bull. Soc. Math. France 123 (1995), 425–475.CrossRefGoogle Scholar
Hida, H., Automorphic induction and Leopoldt type conjectures for $\operatorname {GL}(n)$, Asian J. Math. 2 (1998), 667–710.CrossRefGoogle Scholar
Jacquet, H. and Shalika, J., Exterior square $L$-functions. In Automorphic forms, Shimura varieties, and $L$-functions, Vol. II, Perspectives in Mathematics, vol. 10, eds L. Clozel and J. S. Milne (Academic Press, Boston, MA, 1990), 143–226.Google Scholar
Jantzen, J. C., Representations of algebraic groups, Mathematical Surveys and Monographs, vol. 107 (American Mathematical Society, Providence, RI, 2003).Google Scholar
Januszewski, F., On p-adic L-functions for $\operatorname {GL}(n)\times \operatorname {GL}(n-1)$ over totally real fields, Int. Math. Res. Not. IMRN 2015 (2015), 7884–7949.CrossRefGoogle Scholar
Januszewski, F., On period relations for automorphic $L$-functions II, Preprint (2016), arXiv:1504.06973.Google Scholar
Januszewski, F., Non-abelian p-adic Rankin-Selberg $L$-functions and non-vanishing of central $L$-values, Preprint (2018), arXiv:1708.02616.Google Scholar
Luo, W., Non-vanishing of L-functions for $\operatorname {GL}_n(\mathbb {A}_\mathbb {Q})$, Duke Math. J. 128 (2005), 199–207.CrossRefGoogle Scholar
Nien, C., Uniqueness of Shalika models, Canad. J. Math. 61 (2009), 1325–1340.CrossRefGoogle Scholar
Raghuram, A., On the special values of certain Rankin-Selberg $L$-functions and applications to odd symmetric power $L$-functions of modular forms, Int. Math. Res. Not. IMRN 2010 (2010), 334–372.CrossRefGoogle Scholar
Raghuram, A., Critical values of Rankin–Selberg $L$-functions for $\operatorname {GL}_n \times \operatorname {GL}_{n-1}$ and the symmetric cube $L$-functions for $\operatorname {GL}_2$, Forum Math. 28 (2016), 457–489.CrossRefGoogle Scholar
Raghuram, A. and Shahidi, F., On certain period relations for cusp forms on $\operatorname {GL}_n$, Int. Math. Res. Not. IMRN 2008 (2008), rnn077.Google Scholar
Rohrlich, D., Nonvanishing of $L$-functions for $\operatorname {GL}(2)$, Invent. Math. 97 (1989), 381–403.CrossRefGoogle Scholar
Shimura, G., On the periods of modular forms, Math. Ann. 229 (1977), 211–221.CrossRefGoogle Scholar
Sun, B., Cohomologically induced distinguished representations and cohomological test vectors, Duke Math. J. 168 (2019), 85–126.CrossRefGoogle Scholar