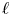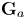Local monodromy of Drinfeld modules

Abstract

Compared with algebraic varieties the local monodromy of Drinfeld modules appears to be hopelessly complex: the image of the wild inertia subgroup under Tate module representations is infinite save for the case of potential good reduction. Nonetheless, we show that Tate modules of Drinfeld modules are ramified in a limited way: the image of a sufficiently deep ramification subgroup is trivial. This leads to a new invariant, the local conductor of a Drinfeld module. We establish an upper bound on the conductor in terms of the volume of the period lattice. As an intermediate step we develop a theory of normed lattices in function field arithmetic including the notion of volume. We relate normed lattices to vector bundles on projective curves. With the aid of Castelnuovo–Mumford regularity this implies a volume bound on norms of lattice generators, and the conductor inequality follows. Last but not least we describe the image of inertia for Drinfeld modules with period lattices of rank $1$. Just as in the theory of local $\ell$-adic Galois representations this image is commensurable with a commutative unipotent algebraic subgroup. However, in the case of Drinfeld modules such a subgroup can be a product of several copies of $\mathbf {G}_a$.

Introduction

Let $K$ be a local field of positive characteristic and let $E$ be a Drinfeld module of finite residual characteristic over $\operatorname {Spec} K$ (cf. § 2.3 and see § 2.4 for the terminology). Pick a separable closure $K^s/K$. We investigate the action of the inertia subgroup $I_K \subset \operatorname {Gal}(K^s/K)$ on the Tate modules $T_\mathfrak {p} E$. This parallels the study of local monodromy in the $\ell$-adic cohomology theory.

In the $\ell$-adic theory one assumes that the prime $\ell$ is different from the residual characteristic of the base field. By way of analogy we suppose that the prime $\mathfrak {p}$ is different from the residual characteristic $\bar {\mathfrak {p}}$ of the Drinfeld module $E$. The case $\mathfrak {p} = \bar {\mathfrak {p}}$ belongs to a function field analogue of Fontaine's theory, and is the subject of a separate study.

Even under the assumption $\mathfrak {p} \ne \bar {\mathfrak {p}}$ the local monodromy of Drinfeld modules is much more complicated than that of algebraic varieties. The good reduction criterion of Takahashi implies that the image of the wild inertia in $\operatorname {GL}(T_\mathfrak {p} E)$ is infinite unless $E$ has potential good reduction.

However, there is a limit on the ramification. Recall that the inertia subgroup $I_K$ carries a descending filtration by closed normal subgroups $I_K^{u}$, $u \in \mathbf {Q}_{\geqslant 0}$, the ramification filtration in upper numbering.

Theorem 1 Let $E$ be a Drinfeld module of finite residual characteristic $\bar {\mathfrak {p}}$ over $\operatorname {Spec} K$. Then there is a rational number $u\geqslant 0$ such that for every prime $\mathfrak {p}\ne \bar {\mathfrak {p}}$ the ramification subgroup $I_K^{u}$ acts trivially on the Tate module $T_\mathfrak {p} E$.

The author first deduced this result from a $z$-adic analogue of Grothendieck's $\ell$-adic monodromy theorem. The $z$-adic monodromy theorem applies in the generality of arbitrary $A$-motives, and will be published in a forthcoming article. A direct and less technically involved proof of Theorem 1 was found by Richard Pink after some discussions with the current author. In this paper, the author would like to present a revision of Pink's argument (Theorem 3.2.4(1)) together with related results.

Replacing $K$ by a finite separable extension we are free to assume that the Drinfeld module $E$ has stable reduction. This means that $E$ is an analytic quotient of a Drinfeld module $D$ of good reduction by a period lattice $\varLambda \subset D(K^s)$, cf. § 4.1. Let us further assume that the lattice $\varLambda$ is defined over $K$, which is to say, $\varLambda \subset D(K)$. Then the action of the inertia group $I_K$ on $T_\mathfrak {p} E$ factors through the maximal abelian quotient $I_K^{\text {ab}}$. By the Hasse–Arf theorem the induced ramification filtration of $I_K^{\text {ab}}$ is integrally indexed, so we can make the following definition.

Definition The local conductor $\operatorname {\mathfrak {f}}(E/K)$ is the least integer $m\geqslant 0$ such that the ramification subgroup $\smash {I_K^{{\text {ab}},m+1}}$ acts trivially on $T_\mathfrak {p} E$ for all $\mathfrak {p}\ne \bar {\mathfrak {p}}$.

The conductor is zero if and only if $\varLambda = 0$, i.e. if the Drinfeld module $E$ has good reduction. Otherwise, the conductor is a positive integer that is prime to $p$. An important property of the conductor is its invariance under isogenies.

The conductor is hard to compute, and we can do it only for special period lattices (Theorem 4.1.13). In general, we can bound the conductor from above by a more amenable invariant.

In the following, let us denote by $A$ the chosen coefficient ring of our Drinfeld modules, cf. § 2.3. This ring is a Dedekind domain over $\mathbf {F}_{\hspace {-1.5pt} q}$ with finite group of units. The period lattice $\varLambda$ carries a natural structure of a finitely generated projective $A$-module.

Poonen [Poo95] introduced the notion of canonical local height. This provides the period lattice $\varLambda$ with a natural norm. Building on the work of Taguchi [Tag93, § 4] we develop a theory of normed $A$-lattices in function field arithmetic (§ 1) and, in particular, define the volume of such lattices.

Theorem 2 Let $E$ be a Drinfeld $A$-module of stable reduction over $\operatorname {Spec} K$ with the local period lattice $\varLambda$ defined over $K$. Let $r$ be the rank of $E$. Then we have an inequality

\[ \operatorname{\mathfrak{f}}(E/K) \leqslant \operatorname{vol}(\varLambda)^s \cdot C^{s(r-s)}, \]

where $\operatorname {vol}(\varLambda )$ is the volume of the period lattice, $s = r - \operatorname {rank}_A(\varLambda )$ and $C$ is an effective constant that depends only on $A$.

To prove this bound we set up a correspondence between normed $A$-lattices and systems of vector bundles on the compactification of the curve $\operatorname {Spec} A$. For such bundles one has a classical criterion of global generation via Castelnuovo–Mumford regularity. Translated to the setting of lattices this gives a volume bound on norms of generators, and the conductor inequality follows.

The bound of Theorem 2 is effective in the following sense: there is an algorithm which calculates $\operatorname {vol}(\varLambda )$ from the $\tau$-polynomials defining the Drinfeld module $E$. This will be demonstrated in a forthcoming article.

Asayama and Huang [AH24, Hua24] introduced the notion of a conductor for Drinfeld modules of rank $2$ and proved a version of Szpiro's conjecture under additional assumptions. It would be interesting to know the precise relation between the conductor of Asayama and Huang and the conductor of this paper.

Last but not least, we study the image of inertia in $\operatorname {GL}(T_\mathfrak {p} E)$. The following result can be seen as a local open image theorem for Drinfeld modules with period lattices of rank $1$.

Theorem 3 Let $E$ be a Drinfeld module of finite residual characteristic $\bar {\mathfrak {p}}$ and rank $r$ over $\operatorname {Spec} K$. Suppose that the local period lattice of $E$ has rank $1$. Then for each prime $\mathfrak {p}\ne \bar {\mathfrak {p}}$ the image of inertia in $\operatorname {GL}(T_\mathfrak {p} E)$ is commensurable with a closed algebraic subgroup $U \cong (\mathbf {G}_a)^{\times (r-1)}$.

Let $V$ be a local $\ell$-adic Galois representation. The $\ell$-adic monodromy theorem of Grothendieck implies that the image of inertia in $\operatorname {GL}(V)$ is commensurable with a closed algebraic subgroup $U \cong (\mathbf {G}_a)^{\times d}$, but the dimension $d$ can only be $0$ or $1$. Theorem 3 shows that in the case of Drinfeld modules the dimension $d$ can be as large as $\dim (V) - 1$.

The situation with Drinfeld modules that have period lattices of rank at least $2$ is made complicated by the presence of nontrivial endomorphisms. Still one expects that a suitable local open image theorem holds in all cases. This is a subject of current research.

Finally, let us discuss the proofs of Theorems 1, 2 and 3. Replacing $K$ with a finite separable extension we are free to assume that the Drinfeld module $E$ is an analytic quotient of a Drinfeld module $D$ of good reduction by a period lattice $\varLambda \subset D(K)$. For each prime $\mathfrak {p}\ne \bar {\mathfrak {p}}$ we then have a short exact sequence of $G_K$-modules

with $A_\mathfrak {p}$ the $\mathfrak {p}$-adic completion of $A$. The inertia group $I_K$ acts trivially on the first and the last module. Consequently, the action of $I_K$ on $T_\mathfrak {p} E$ differs from the identity by a homomorphism $I_K \to \operatorname {Hom}_A(\varLambda,\,T_\mathfrak {p} D)$. This homomorphism can be equally seen as a pairing

\[ \varLambda \times I_K \to T_\mathfrak{p} D. \]

In the exact same way as in the theory of abelian varieties, this pairing turns out to be the restriction to $\varLambda$ of a certain universal pairing

\[ [\ ,\ )_{}\colon D(K) \times I_K \to T_\mathfrak{p} D, \]

the $\mathfrak {p}$-adic Kummer pairing of $D$.

The Kummer pairing from the theory of abelian varieties factors through the tame quotient of the inertia group $I_K$. This quotient group is procyclic of order prime to the residual characteristic $p$ of $K$. By contrast, the Kummer pairing of the Drinfeld module $D$ factors through the maximal quotient $J_K = I_K^{\text {ab}}/(I_K^{\text {ab}})^{\times p}$ that is abelian of exponent $p$. Unlike the tame quotient, the induced ramification filtration on $J_K$ is nontrivial and, in fact, has a break at every positive integer that is prime to $p$.

We study how the Kummer pairing of $D$ interacts with the ramification filtration on $J_K$. We prove that for each element $\lambda \in D(K)$ the homomorphism $[\lambda, \,)_{}\colon J_K \to T_\mathfrak {p} D$ vanishes on a sufficiently deep ramification subgroup $J_K^u$ with $u$ bounded from above by the Poonen height of $\lambda$, see Theorem 3.2.4. This property of the Kummer pairing implies Theorems 1 and 2.

We also prove that the homomorphism $[\lambda, \,)_{}\colon J_K \to T_\mathfrak {p} D$ has open image provided that $\lambda$ is not contained in the subset of integral elements $D(\mathcal {O}_K)$, see Theorem 3.3.2. This property implies Theorem 3.

The Stacks Project

We will use The Stacks Project [Sta] as a source for algebraic geometry. References to The Stacks Project have the form [St: $wxyz$] where ‘$wxyz$’ is a combination of letters and numbers. The corresponding item is located at https://stacks.math.columbia.edu/tag/ $wxyz$.

1. Normed lattices

Recall that a lattice in the sense of geometry of numbers is a finitely generated free $\mathbf {Z}$-module $L$ equipped with a positive-definite quadratic form $q\colon L \to \mathbf {R}_{\geqslant 0}$. The induced norm $\|\cdot \| = \sqrt {q(\cdot )}$ is homogeneous with respect to the archimedean absolute value: we have $\|a v\| = |a| \cdot \|v\|$ for all integers $a \in \mathbf {Z}$ and vectors $v \in L$.

We shall transfer the notion of a normed lattice to the setting of function fields. To this end we draw upon an informal analogy between the pair $(\mathbf {Q}, \infty )$ consisting of the field of rational numbers $\mathbf {Q}$ and its unique archimedean place, and the pair $(F, \infty )$ consisting of a global function field $F$ and an arbitrarily chosen place $\infty$.

The ring $\mathbf {Z}$ is the set of elements $x\in \mathbf {Q}$ which are regular away from $\infty$ and the field $\mathbf {R}$ is the completion of $\mathbf {Q}$ at $\infty$. In the same way, the pair $(F, \infty )$ determines a Dedekind domain $A$ and a locally compact field $F_\infty$. One can consider the pair of rings $A\subset F_\infty$ as a function field equivalent of the pair $\mathbf {Z}\subset \mathbf {R}$.

Inspired by this observation we define an $A$-lattice as a finitely generated projective $A$-module $\varLambda$ equipped with a norm $\|\cdot \|\colon \varLambda \to \mathbf {R}_{\geqslant 0}$ which is homogeneous with respect to a fixed $\infty$-adic absolute value on $F_\infty$ and induces the discrete topology on $\varLambda$. The study of normed lattices in function field arithmetic was initiated by Taguchi [Tag93, § 4]. We develop the theory further by relating normed lattices to vector bundles on the smooth projective curve $X$ which has $F$ as the field of rational functions.

As is the case for $\mathbf {Z}$-lattices the norm of an $A$-lattice $\varLambda$ extends uniquely to a norm on the ‘real’ vector space $V_\infty = F_\infty \otimes _A \varLambda$ but this result is rather subtle. One then defines the volume of the lattice $\varLambda$ as a normalized volume of its fundamental domain in the locally compact vector space $V_\infty$. The relation between lattices and vector bundles leads to a bound on norms of generators in terms of the volume (Theorem 1.6.4).

In [Tag93, § 4] Taguchi defined the discriminant of a lattice. At the moment it is not clear what is the precise relation between the volume as defined in this paper and the discriminant of Taguchi.

1.1 Normed vector spaces

As a preparation for the theory of lattices let us review some properties of normed vector spaces following [BGR84, Ch. 2]. We fix a field $F$ and an absolute value $|\cdot |\colon F \to \mathbf {R}_{\geqslant 0}$ that arises from a nontrivial discrete valuation. Let $R = \{ x \in F, |x| \leqslant 1 \}$ be the corresponding ring of integers. We denote its maximal ideal by $\mathfrak {p}$.

Let $V$ be a finite-dimensional $F$-vector space. Recall that a $\mathfrak {p}$-adic norm on $V$ is a map $\|\cdot \|\colon V \to \mathbf {R}_{\geqslant 0}$ with the following properties:

1. (${\rm V} _{\!1 }$) $\|v\| = 0$ if and only if $v = 0$;

2. (${\rm V} _{\!2 }$) $\|v + v'\| \leqslant \max \{ \|v\|, \|v'\| \}$;

3. (${\rm V} _{\!3 }$) $\|x v\| = |x| \cdot \|v\|$ for all $x \in F$.

We have $\|{-}v\| = \|v\|$ by the homogeneity property (${\rm V}_{\!3}$), so the ultrametric inequality (${\rm V}_{\!2}$) becomes an equality when $\|v\|\ne \|v'\|$.

Let $\pi \in F$ be a uniformizer and set $\varepsilon := |\pi |$. Observe that $\varepsilon \in (0, 1)$.

Lemma 1.1.1 The image of the norm function $\|\cdot \|\colon V \to \mathbf {R}_{\geqslant 0}$ has the form

\[ r_1 \varepsilon^{\mathbf {Z}} \cup \dotsb \cup r_m \varepsilon^{\mathbf {Z}} \cup \{0\}, \]

where $r_1, r_2, \dotsc, r_m \in (\varepsilon,\:1]$ is a sequence of real numbers, $m\leqslant \dim V$.

Proof. The set of values $|F^\times | = \varepsilon ^{\mathbf {Z}}$ is a subgroup of $\mathbf {R}^\times$, so the claim follows by [BGR84, Prop. 2.1.4/2].

The ultrametric inequality (${\rm V}_{\!2}$) and the homogeneity property (${\rm V}_{\!3}$) imply that the balls

\[ B(V,\,r) = \{v \in V, \, \|v\| \leqslant r \}, \quad r \in \mathbf {R}_{>0}, \]

are $R$-submodules of $V$ such that:

1. $({\rm B} _{ 1 } )$ $x\,B(V,\,r) = B(V,\,|x|\,r)$ for every scalar $x \in F^\times$;

2. $({\rm B} _{ 2 } )$ $F \otimes _{R} B(V,\,r) = V$.

Lemma 1.1.2 For each pair of real numbers $r' > r > 0$ the quotient $R$-module $B(V,\,r')/B(V,\,r)$ has finite length.

Proof. It suffices to prove the claim for $r = r'\varepsilon ^n$ with any integer $n>0$. The $R$-module $B(V,\,r')$ is torsion-free by construction and has finite rank by property $({\rm B}_2)$. We also have $B(V,\,r) = \mathfrak {p}^nB(V,\,r')$ by property $({\rm B}_1)$. Invoking Lemma 3 of [Poo95, § 5] we conclude that the $R/\mathfrak {p}^n$-module $B(V,\,r')/B(V,\,r)$ is finitely generated and, thus, has finite length.

Each norm endows the vector space $V$ with a topology by means of the fundamental system $\{B(V,\,r)\}_{r>0}$. Lemma 1.1.1 implies that this system is the same as the system of open balls $\{ v \in V, \|v\| < r \}$.

It is important to note that, in general, the norm topology on $V$ can be coarser than the canonical $\mathfrak {p}$-adic topology. An explicit construction of such norms is given in Example 1.1.7. From Lemma 1.1.2 we directly have the following result.

Corollary 1.1.3 A norm on $V$ induces the canonical $\mathfrak {p}$-adic topology if and only if for each real number $r > 0$ the $R$-module $B(V,\,r)$ is finitely generated.

To increase flexibility we will need the notion of a seminorm which is a map $\|\cdot \|\colon V \to \mathbf {R}_{\geqslant 0}$ satisfying the conditions (${\rm V}_{\!2}$) and (${\rm V}_{\!3}$). The following claim is easy to check.

Lemma 1.1.4 For each seminorm $\|\cdot \|\colon V \to \mathbf {R}_{\geqslant 0}$ the following hold.

1. (1) The kernel $H = \{ v \in V, \:\|v\| = 0 \}$ is an $F$-vector subspace of $V$.

2. (2) The map $\|\cdot \|$ factors through the quotient homomorphism $V \twoheadrightarrow V/H$ and induces a norm on $V/H$.

Next we give a criterion for the norm on $V$ to induce the canonical $\mathfrak {p}$-adic topology. Let $\smash {F_{\mathfrak {p}}}$ be the $\mathfrak {p}$-adic completion of the field $F$.

Theorem 1.1.5 Each norm on the vector space $V$ extends uniquely to a seminorm on the $\mathfrak {p}$-adic completion $\smash {V_{\mathfrak {p}}} = \smash {F_{\mathfrak {p}}}\otimes _{F} V$, and such an extension is a norm if and only if the original norm induces the $\mathfrak {p}$-adic topology on $V$.

Proof. It follows from Proposition 1 of [Bou81, II, § 1, n${}^\circ$1] that every seminorm is continuous with respect to the $\mathfrak {p}$-adic topology on $\smash {V_{\mathfrak {p}}}$ and the analytic topology on $\mathbf {R}_{\geqslant 0}$. Since the vector space $V$ is $\mathfrak {p}$-adically dense in $\smash {V_{\mathfrak {p}}}$ we conclude that the sought extension is unique.

Let ${V_{\rho }}$ be the completion of the normed vector space $V$ as in [BGR84, § 2.1.3]. This is a normed $\smash {F_{\mathfrak {p}}}$-vector space by construction. The proof of [BGR84, Prop. 2.3.3/6] shows that the natural morphism $\smash {V_{\mathfrak {p}}} \twoheadrightarrow {V_{\rho }}$ is surjective. Taking the composition of the norm on ${V_{\rho }}$ with the surjection $\smash {V_{\mathfrak {p}}} \twoheadrightarrow {V_{\rho }}$ we obtain the desired seminorm on the vector space $\smash {V_{\mathfrak {p}}}$.

The seminorm on $\smash {V_{\mathfrak {p}}}$ is a norm if and only if the surjection $\smash {V_{\mathfrak {p}}}\twoheadrightarrow {V_{\rho }}$ is an isomorphism. According to [BGR84, Prop. 2.3.3/6] the latter happens if and only if the norm topology on $V$ is the canonical $\mathfrak {p}$-adic topology, as claimed.

Corollary 1.1.6 Suppose that the field $F$ is $\mathfrak {p}$-adically complete. Then the norm topology on $V$ is the canonical $\mathfrak {p}$-adic topology.

The behaviour of $\mathfrak {p}$-adic norms in Theorem 1.1.5 resembles the behaviour of real-valued quadratic forms on a finite-dimensional $\mathbf {Q}$-vector space $V$. Every such form $q$ extends uniquely to the real vector space $V_\infty = \mathbf {R}\otimes _{\mathbf {Q}} V$. If the form $q$ takes strictly positive values on $V\smallsetminus \{0\}$ then it is positive-semidefinite, and the map $v \mapsto q(v)^{1/2}$ is an archimedean seminorm on $V_\infty$. This seminorm is a norm if and only if the form $q$ is positive-definite. Comparing with Theorem 1.1.5, we conclude that the property of inducing the $\mathfrak {p}$-adic topology can be understood as a form of positive-definiteness for $\mathfrak {p}$-adic norms.

As an offshoot of Theorem 1.1.5 we get a description of all norms that fail to induce the $\mathfrak {p}$-adic topology on $V$.

Example 1.1.7 Suppose that $\dim V \geqslant 2$, and that the field $F$ is not $\mathfrak {p}$-adically complete. Pick a nonzero subspace $H \subset \smash {V_{\mathfrak {p}}}$ which is totally irrational in the sense that $H \cap V = \{0\}$. Pick a norm on the quotient $\smash {V_{\mathfrak {p}}}/H$. The natural morphism $V\hookrightarrow \smash {V_{\mathfrak {p}}}/H$ is injective by construction, so we obtain a norm on $V$ by composition with the chosen norm on $\smash {V_{\mathfrak {p}}}/H$.

Theorem 1.1.5 implies that the norm topology on $V$ is not $\mathfrak {p}$-adic as otherwise the subspace $H$ will be zero. It follows by Corollary 1.1.3 that the balls $B(V,\,r)$ are not finitely generated as $R$-modules. Theorem 1.1.5 also implies that varying the choices of $H$ and of the norm on $\smash {V_{\mathfrak {p}}}/H$ one obtains every norm on $V$ that does not induce the $\mathfrak {p}$-adic topology.

1.2 The setting

From now on we fix a global function field $F$ and a place $\infty$ of $F$. We will use the following notation:

• – $\kappa \subset F$ is the ring of elements which are regular at all places;

• – $A \subset F$ is the ring of elements which are regular outside $\infty$;

• – $\mathcal {O}_{F,\infty } \subset F$ is the ring of elements which are regular at $\infty$;

• – $F_\infty$ is the $\infty$-adic completion of $F$;

• – $\kappa _\infty$ is the residue field of $F_\infty$ (and of $\mathcal {O}_{F,\infty }$);

• – $c = |\kappa _\infty |$ is the cardinality of this residue field.

Fix an $\infty$-adic absolute value $|\cdot |_\infty \colon F_\infty \to \mathbf {R}_{\geqslant 0}$ such that $|\pi |_\infty ^{-1} = c$ for a uniformizer $\pi \in F_\infty$. Although our theory works with any normalization, this particular choice leads to better-looking formulas.

The ring $\kappa$ is a finite field, called the field of constants of $F$. The ring $A$ is a Dedekind domain of finite type over $\kappa$. We will refer to $A$ as the coefficient ring and it will serve us as an analogue of the ring of integers $\mathbf {Z}$. The local field $F_\infty$ will play the role of the field of real numbers $\mathbf {R}$.

1.3 Lattices

Let $\varLambda$ be a finitely generated projective $A$-module. An $\infty$-adic norm on $\varLambda$ is a map $\|\cdot \|\colon \varLambda \to \mathbf {R}_{\geqslant 0}$ such that:

1. (Λ ₁) $\|\lambda \| = 0$ if and only if $\lambda = 0$;

2. (Λ ₂) $\|\lambda + \lambda '\| \leqslant \max \{ \|\lambda \|, \|\lambda '\| \}$;

3. (Λ ₃) $\|a\lambda \| = |a|_\infty \|\lambda \|$ for all $a \in A$.

Following the construction in [BGR84, § 2.1.3] every such norm extends uniquely to an $\infty$-adic norm on the rational vector space

\[ V = F \otimes_A \varLambda. \]

We will apply the considerations of § 1.1 to the normed vector space $V$. By analogy with § 1.1 we define the following subsets of $\varLambda$:

\[ B(\varLambda,\,r) = \{\lambda\in\varLambda,\:\|\lambda\| \leqslant r\}, \quad r \in \mathbf {R}_{>0}. \]

This time $B(\varLambda,\,r)$ is merely a $\kappa$-vector space.

Lemma 1.3.1 For each pair of real numbers $r' > r > 0$ the subspace $B(\varLambda,\,r)$ has finite index in $B(\varLambda,\,r')$.

Proof. By construction, $B(\varLambda,\,s) = \varLambda \cap B(V,\,s)$ for all $s > 0$. We thus have an inclusion of $\kappa$-vector spaces

\[ \frac{B(\varLambda,\,r')}{B(\varLambda,\,r)} \hookrightarrow \frac{B(V,\,r')}{B(V,\,r)}, \]

and the claim follows from Lemma 1.1.2.

We are ready for the main definition of this section.

Definition 1.3.2 An $A$-lattice is a finitely generated projective $A$-module $\varLambda$ supplied with an $\infty$-adic norm $\|\cdot \|$ that induces the discrete topology on $\varLambda$.

In other words there is a real number $\varepsilon >0$ such that every nonzero lattice vector $\lambda$ satisfies $\|\lambda \| \geqslant \varepsilon$. By Lemma 1.3.1 this holds if and only if the subsets $\{\lambda \in \varLambda,\:\|\lambda \| \leqslant r\}$ are finite for every $r > 0$.

A norm can induce a non-discrete topology on $\varLambda$. All such norms are described in Example 1.1.7 above.

The discreteness condition of Definition 1.3.2 can be seen as a function field analogue of positive-definiteness. Let $q$ be a real-valued quadratic form on a finitely generated free $\mathbf {Z}$-module $L$. Suppose that the form $q$ takes strictly positive values on $L \smallsetminus \{0\}$. Then $q$ is positive-semidefinite as a quadratic form on the real vector space $\mathbf {R}\otimes _{\mathbf {Z}} L$, and is positive-definite if and only if for each real number $r > 0$ the set $\{v \in L, \,q(v) \leqslant r \}$ is finite, cf. Lemma 9.5 of [Sil09, VIII.9].

Theorem 1.3.3 Let $\varLambda$ be a lattice. Then the norm on $\varLambda$ extends to a unique $\infty$-adic norm on the vector space $V_\infty = F_\infty \otimes _A \varLambda$.

Proof. We have observed previously that the norm on $\varLambda$ extends uniquely to an $\infty$-adic norm on the rational vector space $V = F\otimes _A \varLambda$. By Theorem 1.1.5 the norm on $V$ extends to a unique seminorm on $V_\infty$. Let $H$ be the kernel of this seminorm and consider the quotient vector space $W = V_\infty /H$. The seminorm on $V_\infty$ is the composite of the surjection $V_\infty \twoheadrightarrow W$ and a norm on $W$.

The lattice $\varLambda$ injects into the quotient vector space $W$. By assumption, the sets $B(\varLambda,\,r)$ are finite for all $r > 0$ so $\varLambda$ is discrete in $W$ with respect to the norm topology. As the field $F_\infty$ is $\infty$-adically complete it follows by Corollary 1.1.6 that the norm topology on $W$ is the canonical $\infty$-adic topology. The fact that $\varLambda$ is discrete in $W$ thus implies that $\operatorname {rank} \varLambda \leqslant \dim W$. As $\operatorname {rank}\varLambda = \dim V_\infty$ we deduce that $H = 0$.

Corollary 1.3.4 Let $\varLambda$ be a lattice, and consider the rational vector space $V = F\otimes _A \varLambda$ with the induced norm. Then for each real number $r > 0$ the ball $B(V,\,r)$ is finitely generated as a module over the ring $\mathcal {O}_{F,\infty }$.

Proof. The norm on $V$ extends to a norm on $V_\infty$ by Theorem 1.3.3, so invoking Theorem 1.1.5 we derive that the norm topology on $V$ is the canonical $\infty$-adic topology. The claim then follows by Corollary 1.1.3.

1.4 Lattices and vector bundles

We shall relate lattices to vector bundles on the smooth projective curve $X$ over $\operatorname {Spec} \kappa$ which compactifies the affine curve $Y = \operatorname {Spec} A$. By construction we have $X\smallsetminus Y = \{\infty \}$. Let us denote by $\mathcal {O}_X({-}\infty )$ the ideal sheaf of the reduced closed subscheme $\{\infty \} \subset X$.

Pick a lattice $\varLambda$, set $V = F\otimes _A \varLambda$, and let $\mathcal {E}_{\varLambda }$ be the locally free sheaf on the curve $Y$ induced by the $A$-module $\varLambda$. Let $r > 0$ be a real number.

Definition 1.4.1 The quasi-coherent sheaf $\mathcal {E}_{\varLambda, r}$ on the curve $X$ is constructed by gluing the locally free sheaf $\mathcal {E}_{\varLambda }$ to the $\mathcal {O}_{F,\infty }$-module $B(V,\,r)$ via the canonical isomorphism

\[ F\otimes_A \varLambda \xrightarrow{\smash{{{\sim}}}} V \xrightarrow{\smash{{{\sim}}}} F\otimes_{\mathcal{O}_{F,\infty}} B(V,\,r). \]

Theorem 1.4.2 The sheaf $\mathcal {E}_{\varLambda, r}$ has the following properties.

1. (1) The sheaf $\mathcal {E}_{\varLambda, r}$ is locally free of finite rank.

2. (2) $H^0(X,\:\mathcal {E}_{\varLambda, r}) = \{\lambda \in \varLambda,\:\|\lambda \| \leqslant r\}$.

3. (3) For every $i \in \mathbf {Z}$ we have $\mathcal {E}_{\varLambda, r}(i\infty ) = \mathcal {E}_{\varLambda, r c^i}$.

Proof. Property (1) follows from Corollary 1.3.4 and property (2) is immediate. To show property (3) note that the locally free sheaf $\mathcal {E}_{\varLambda, r}(i\infty )$ is obtained by gluing the sheaves induced by the modules $\varLambda$ and $\pi ^{-i} B(V,\,r)$ with $\pi$ a uniformizer of $\mathcal {O}_{F,\infty }$. The claim follows since $\pi ^{-i} B(V,\,r) = B(V,\,r c^i)$.

Combining Theorem 1.4.2 with Lemma 1.1.1 we obtain a correspondence between lattices and systems of vector bundles.

Corollary 1.4.3 There is a one-to-one correspondence between $A$-lattices and pairs which consist of (i) a strictly increasing chain of locally free sheaves

\[ \mathcal{E}_1 \subset \dotsb \subset \mathcal{E}_m \subset \mathcal{E}_1(\infty) \]

on the complete curve $X$ such that $\mathcal {E}_i|_Y = \mathcal {E}_{i+1}|_Y$ for all $i \in \{1, \dotsc, m -1 \}$, and (ii) a sequence of real numbers

\[ \{ r_1 < \dotsb < r_m \} \subset (c^{-1}, 1]. \]

The $A$-module $\varLambda = H^0(Y,\mathcal {E}_i)$ is finitely generated projective and is independent of the choice of $i$. It carries a filtration by $\kappa$-vector spaces $H^0(X,\mathcal {E}_i(j\infty ))$ with $i \in \{1,\dotsc,m\}$ and $j \in \mathbf {Z}$. For each element $\lambda \in \varLambda$ we set

\[ \|\lambda\| = \inf \{r_i c^j \:|\: \lambda \in H^0(X,\,\mathcal{E}_i(j\infty))\}. \]

It is easy to check that the function $\|\cdot \|$ is a norm on $\varLambda$. The normed module $\varLambda$ is a lattice since the vector spaces $H^0(X,\mathcal {E}_i(j\infty ))$ are finite-dimensional.

1.5 The volume

Let $\varLambda$ be a lattice, and consider the vector space $V_\infty = F_\infty \otimes _A \varLambda$ with the induced norm. By Corollary 1.1.6 the norm topology on $V_\infty$ is the canonical $\infty$-adic topology. For each real number $r > 0$ the ball $B(V_\infty,\,r)$ is thus compact and open, and we can make the following definition.

Definition 1.5.1 The $r$-normalized volume of $\varLambda$ is defined by the formula

\[ \operatorname{vol}(\varLambda,\,r) = \mu(V_\infty/\varLambda), \]

where $\mu$ is the unique translation-invariant Haar measure on $V_\infty$ satisfying $\mu (B(V_\infty,\,r)) = 1$. In the case $r = 1$ we will use the simplified notation:

\[ \operatorname{vol}(\varLambda) = \operatorname{vol}(\varLambda,\,1). \]

Denoting by $n$ the rank of the lattice $\varLambda$ we have an equality for every integer $i$:

\[ \operatorname{vol}(\varLambda,\,r c^i) = c^{-ni} \operatorname{vol}(\varLambda,\,r). \]

This results from the fact that $\mu (B(V_\infty,\,r c^i)) = c^{ni} \,\mu (B(V_\infty,\,r))$ for every translation-invariant Haar measure $\mu$.

In the following we denote by $\chi$ the Euler characteristic of coherent sheaves on the curve $X\to \operatorname {Spec}\kappa$.

Lemma 1.5.2 We have $\operatorname {vol}(\varLambda,\,r) = {|\kappa |}^{-\chi (\mathcal {E}_{\varLambda, r})}$.

Proof. The cohomology of the locally free sheaf $\mathcal {E}_{\varLambda, r}$ is computed by a Čech complex

concentrated in degrees $0$ and $1$. We rewrite this complex as follows:

Thus, for every translation-invariant Haar measure $\mu$ on $V_\infty$ we have an equality:

\[ \frac{\mu(V_\infty/\varLambda)}{\mu(B(V_\infty,\,r))} = \frac{|H^1(X,\mathcal{E}_{\varLambda, r})|}{|H^0(X,\mathcal{E}_{\varLambda, r})|}. \]

The claim follows.

As in the case of $\mathbf {Z}$-lattices we can compute the volume of an $A$-lattice via the absolute value of a determinant. In the following formula, we treat the respective wedge products as elements of one-dimensional $F_\infty$-vector space $\det (V_\infty )$. Their quotient is a well-defined element of $F_\infty ^\times$.

Lemma 1.5.3 Pick a basis $v_1, \dotsc, v_n$ of the free module $B(V_\infty,\,r)$ and pick vectors $\lambda _1,\dotsc,\lambda _n$ generating a submodule of finite index $e$ in $\varLambda$. Then

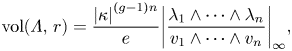\[ \operatorname{vol}(\varLambda,\,r) = \frac{{|\kappa|}^{(g-1)n}}{e} \biggl|\frac{\lambda_1 \wedge \dotsb \wedge \lambda_n}{v_1 \wedge \dotsb \wedge v_n} \biggr|_\infty, \]

where $g$ is the genus of the coefficient field $F$.

Proof The product $s = \lambda _1 \wedge \dotsb \wedge \lambda _n$ is a rational section of the invertible sheaf $\det (\mathcal {E}_{\varLambda, r})$. Its order at the point $\infty$ equals

\[ [\kappa_\infty:\kappa] v_\infty \biggl(\frac{\lambda_1 \wedge \dotsb \wedge \lambda_n}{v_1 \wedge \dotsb \wedge v_n} \biggr), \]

where $v_\infty \colon F_\infty ^\times \twoheadrightarrow \mathbf {Z}$ is the normalized $\infty$-adic valuation. Hence,

\[ {|\kappa|}^{-\deg(s)} = \frac{1}{e} \cdot \biggl|\frac{\lambda_1 \wedge \dotsb \wedge \lambda_n}{v_1 \wedge \dotsb \wedge v_n} \biggr|_\infty. \]

The claim then follows from Lemma 1.5.2 and Riemann–Roch formula.

Theorem 1.5.4 Let $\varLambda$ be a lattice of rank $n$ and let $r > 0$ be a real number. Then for all integers $i \gg 0$ we have an equality:

\[ |\{\lambda \in \varLambda, \: \|\lambda\| \leqslant r c^i\}| = \frac{c^{ni}}{\operatorname{vol}(\varLambda,\,r)}. \]

Moreover, for all integers $i$ we have a lower bound:

\[ |\{\lambda \in \varLambda, \: \|\lambda\| \leqslant r c^i\}| \geqslant \frac{c^{ni}}{\operatorname{vol}(\varLambda,\,r)}. \]

Proof. Let $i$ be a non-negative integer. Consider a natural short exact sequence of sheaves on the curve $X$:

The coherent sheaf $\mathcal {F}$ is concentrated at the point $\infty$ and has length $n i$ as an $\mathcal {O}_{X,\infty }$-module. We thus have an equality

\[ \frac{|H^0(X,\mathcal{E}_{\varLambda, r}(i\infty))|}{|H^1(X,\mathcal{E}_{\varLambda, r}(i\infty))|} = c^{ni} \frac{|H^0(X,\mathcal{E}_{\varLambda, r})|}{|H^1(X,\mathcal{E}_{\varLambda, r})|}. \]

By construction we have $H^0(X,\:\mathcal {E}_{\varLambda, r}(i\infty )) = \{\lambda \in \varLambda,\:\|\lambda \| \leqslant r c^i\}$. Hence, Lemma 1.5.2 implies that

\[ \frac{|\{\lambda\in\varLambda,\:\|\lambda\| \leqslant r c^i\}|}{|H^1(X,\mathcal{E}_{\varLambda, r}(i\infty))|} = \frac{c^{ni}}{\operatorname{vol}(\varLambda,\,r)}. \]

The cohomology group $H^1(X,\:\mathcal {E}_{\varLambda, r}(i\infty ))$ vanishes for $i \gg 0$ as the invertible sheaf $\mathcal {O}_X(\infty )$ is ample. The first claim of the theorem follows. To prove the second claim note that $c^{ni} \,\operatorname {vol}(\varLambda,\,r)^{-1} = \operatorname {vol}(\varLambda,\,r c^i)^{-1}$ for each integer $i$. It is thus enough to treat the case $i = 0$ which follows from the displayed formula above.

Corollary 1.5.5 Every lattice $\varLambda$ of rank $n$ contains a nonzero vector of norm at most $c\cdot {\operatorname {vol}(\varLambda )}^{1/n}$.

1.6 A bound on norms of generators

We would like to find a real number $r > 0$ such that the subset $\{\lambda \in \varLambda,\:\|\lambda \| \leqslant r\}$ generates the lattice $\varLambda$. To this end, we will employ the correspondence between lattices and vector bundles. We will use supplementary notation:

• – $g$ is the genus of the smooth projective curve $X\to \operatorname {Spec}\kappa$;

• – $f = [\kappa _\infty :\kappa ]$.

The invertible sheaf $\mathcal {O}_X(\infty )$ has degree $f$. Let us also pick an auxiliary integer $h$ such that the twist $\mathcal {O}_X(h\infty )$ is very ample. We will utilize a classical criterion for global generation of coherent sheaves on curves.

Lemma 1.6.1 Let $\mathcal {E}$ be a coherent sheaf on the curve $X$. If $H^1(X,\mathcal {E}) = 0$, then the sheaf $\mathcal {E}(h\infty )$ is globally generated.

Proof. Let $\iota \colon X \hookrightarrow \mathbf {P}^N$ be the closed embedding defined by global sections of $\mathcal {O}_X(h\infty )$. The coherent sheaf $\iota _*(\mathcal {E})$ is $1$-regular in the sense of Castelnuovo–Mumford [St: 08A3]. Hence, the sheaf $\iota _*(\mathcal {E})(1) = \iota _*(\mathcal {E}(h\infty ))$ is globally generated [St: 08A8].

Lemma 1.6.2 Let $\mathcal {E}$ be a locally free sheaf of rank $n$ on the curve $X$. Set

\[ i = \biggl\lceil\frac{-\deg\mathcal{E} + (2g - 2)n + 1}{f}\biggr\rceil + h. \]

Suppose that the sheaf $\mathcal {E}$ is an iterated extension of invertible sheaves of degree at most $2g - 2$. Then the sheaf $\mathcal {E}(i\infty )$ is globally generated.

Proof. Write the degrees of invertible sheaves in the form $(2g - 2) - e_j$ with $e_j \geqslant 0$. We have $\deg \mathcal {E} = (2g-2)n - \sum e_j$ so that

\[ -e_j - \deg \mathcal{E} + (2g-2)n \geqslant 0. \]

Hence, the sheaf $\mathcal {E}' = \mathcal {E}((i-h)\infty )$ is an iterated extension of invertible sheaves of degree at least $2g-1$. Induction on the number of invertible sheaves implies that $H^1(X,\,\mathcal {E}') = 0$ so the sheaf $\mathcal {E}'(h\infty )$ is globally generated by Lemma 1.6.1.

Lemma 1.6.3 Let $\mathcal {E}$ be a locally free sheaf of rank $n$ on the curve $X$. Set

\[ i = \biggl\lceil\frac{-\deg\mathcal{E} + (2g-2)n + 1}{f}\biggr\rceil + h n. \]

Suppose that $H^0(X,\,\mathcal {E}) = 0$. Then the sheaf $\mathcal {E}(i\infty )$ is globally generated.

Proof. Let $\Omega$ be the canonical sheaf of the curve $X\to \operatorname {Spec}\kappa$ and set $\mathcal {F} = \mathcal {E}^* \otimes \Omega$. Serre duality shows that $H^1(X,\,\mathcal {F}) = 0$ so the sheaf $\mathcal {F}(h\infty )$ is globally generated by Lemma 1.6.1. Dualizing and twisting we get an embedding $\mathcal {E}(-h\infty ) \hookrightarrow \Omega ^{\oplus m}$, $m \gg 0$. Hence the sheaf $\mathcal {E}' = \mathcal {E}(-h\infty )$ is an iterated extension of invertible subsheaves $\mathcal {L} \subset \Omega$. Every such subsheaf has degree at most $2g - 2$. Lemma 1.6.2 implies that the sheaf $\mathcal {E}'((i+h)\infty ) = \mathcal {E}(i\infty )$ is globally generated with

\[ i = \biggl\lceil\frac{-\deg\mathcal{E}'+(2g-2)n + 1}{f}\biggr\rceil. \]

The claim follows since $\deg \mathcal {E}' = \deg \mathcal {E} - f h n$.

Theorem 1.6.4 Let $\varLambda$ be a lattice of rank $n$. Suppose that every nonzero vector of $\varLambda$ has norm at least $1$. Then the $A$-module $\varLambda$ is generated by the subset

\[ \{\lambda\in\varLambda,\:\|\lambda\| \leqslant \operatorname{vol}(\varLambda) \cdot C^n\} \]

with $C = {|\kappa |}^{3g + 2f - 1}$.

Proof. Consider the locally free sheaf $\mathcal {E} = \mathcal {E}_{\varLambda, 1}$. We have

\[ H^0(X,\:\mathcal{E}({-}\infty)) = \{\lambda\in\varLambda,\:\|\lambda\| \leqslant c^{-1}\}. \]

Thus $H^0(X,\mathcal {E}({-}\infty )) = 0$ by our assumption on the length of nonzero lattice vectors. Invoking the Riemann–Roch formula, we deduce that

\[ -\deg(\mathcal{E}({-}\infty)) = -\chi(\mathcal{E}) + (-g + 1 + f) n. \]

Hence, by Lemma 1.6.3 the sheaf $\mathcal {E}((i-1)\infty )$ is globally generated when

\[ i = \biggl\lceil\frac{-\chi(\mathcal{E}) + (g - 1 + f + f h)n + 1}{f}\biggr\rceil. \]

To ensure that the invertible sheaf $\mathcal {O}_X(h\infty )$ is very ample it is enough to take any integer $h$ such that $f h\geqslant 2g + 1$. We thus have an estimate $f h\leqslant 2g + f$, and the sheaf $\mathcal {E}(j\infty )$ is globally generated for an integer $j$ such that

\[ j \leqslant \biggl\lceil\frac{-\chi(\mathcal{E}) + (3g + 2f - 1)n + 1}{f}\biggr\rceil - 1. \]

In particular, the $A$-module $\varLambda = H^0(Y,\:\mathcal {E}(j\infty ))$ is generated by the subset

\[ \{\lambda\in\varLambda,\:\|\lambda\| \leqslant c^j\} = H^0(X,\:\mathcal{E}(j\infty)). \]

Since $c = {|\kappa |}^{f}$, we obtain an estimate

\[ c^j \leqslant {|\kappa|}^{-\chi(\mathcal{E})} \cdot {|\kappa|}^{(3g + 2f - 1)n}. \]

The result follows as ${|\kappa |}^{-\chi (\mathcal {E})} = \operatorname {vol}(\varLambda )$ by Lemma 1.5.2.

In the case $A=\kappa [t]$ the estimate of Theorem 1.6.4 is sharp in all ranks. The lattice $A^{\oplus n}$ with the supremum norm has volume ${|\kappa |}^{-n}$, is generated by vectors of norm $1$ and has no nonzero vectors of norm strictly less than $1$.

2. Preliminaries concerning Drinfeld modules

Fix a field $\mathbf {F}_{\hspace {-1.5pt} q}$ of cardinality $q < \infty$. Let $K$ be a field over $\mathbf {F}_{\hspace {-1.5pt} q}$. In the following, we will refer to $K$ as the base field. Pick a separable closure $K^s/K$ and let $G_K$ be the corresponding absolute Galois group.

2.1 Twisted polynomials

Let $K[\tau ]$ be the twisted polynomial ring. This is the ring of polynomials in a formal variable $\tau$ with coefficients in $K$ and with the multiplication subject to the rule $\tau \,\alpha = \alpha ^q\,\tau$ for all $\alpha \in K$. The elements of $K[\tau ]$ will be referred to as $\tau$-polynomials.

The ring $K[\tau ]$ is the endomorphism ring of the $\mathbf {F}_{\hspace {-1.5pt} q}$-module scheme $\mathbf {G}_a$ over $\operatorname {Spec} K$ with the element $\tau$ corresponding to the $q$-Frobenius. This interpretation allows us to evaluate $\tau$-polynomials at points of $\mathbf {G}_a$.

Lemma 2.1.1 Let $V$ be a finite-dimensional Galois-stable $\mathbf {F}_{\hspace {-1.5pt} q}$-vector subspace of $K^s$ and let $f\colon V \to K^s$ be a Galois-equivariant $\mathbf {F}_{\hspace {-1.5pt} q}$-linear map. Set $n = \dim V$ and suppose that $n > 0$. Then the following hold.

1. (1) There is a unique $\tau$-polynomial of the form

   \[ \varphi = a_0 + a_1 \tau + \dotsb + a_{n-1} \tau^{n-1}, \quad a_i \in K, \]
   which satisfies $\varphi (v) = f(v)$ for all $v \in V$.

2. (2) The coefficients $a_i$ are determined by the equation

   \[ \begin{pmatrix} v_1 & v_1^q & \dotsb & v_1^{q^{n-1}} \\ v_2 & v_2^q & \dotsb & v_2^{q^{n-1}} \\ & & \dotsb & \\ v_n & v_n^q & \dotsb & v_n^{q^{n-1}} \end{pmatrix} \begin{pmatrix} a_0 \\ a_1 \\ \vdots \\ a_{n-1} \end{pmatrix} = \begin{pmatrix} f(v_1) \\ f(v_2) \\ \vdots \\ f(v_n) \end{pmatrix}, \]
   where $v_1, \dotsc, v_n$ is a basis of $V$.

Proof. The determinant of the square matrix in part (2) is the Moore determinant $M(v_1,\dotsc,v_n)$, see [Pap23, Definition 3.1.17]. This determinant is nonzero because the elements $v_1, \dotsc, v_n$ are $\mathbf {F}_{\hspace {-1.5pt} q}$-linearly independent. Hence, the solution vector is uniquely determined.

Consider the polynomial $\varphi = a_0 + a_1 \tau + \dotsb + a_{n-1} \tau ^{n-1}$. By construction, we have $\varphi (v_i) = f(v_i)$ for all $i \in \{1,\dotsc,n\}$ which implies by linearity that $\varphi (v) = f(v)$ for all $v \in V$. It remains to show that the coefficients of $\varphi$ are Galois-invariant and, thus, belong to the subfield $K\subset K^s$.

Apply an automorphism $g \in G_K$ to both sides of the matrix equation in part (2). Since the map $f$ is Galois-equivariant, it follows that the polynomial

\[ {}^g \varphi = g(a_0) + g(a_1) \, \tau + \dotsb + g(a_{n-1}) \, \tau^{n-1} \]

satisfies $({}^g \varphi )(g v_i) = f(g v_i)$ for all $i$. The set $g v_1, \dotsc, g v_n$ is yet another basis of $V$ so the linearity implies that $({}^g \varphi )(v) = f(v)$ for all $v \in V$. In particular, $({}^g \varphi )(v_i) = f(v_i)$ for all $i$. Since the matrix equation in part (2) has a unique solution, we deduce that ${}^g \varphi = \varphi$, and the claim follows.

2.2 Artin–Schreier theory

Let $E$ be an $\mathbf {F}_{\hspace {-1.5pt} q}$-module scheme over $\operatorname {Spec} K$ which is isomorphic to $\mathbf {G}_a$. Consider a separable isogeny $\varphi \colon E \to E$, i.e. an $\mathbf {F}_{\hspace {-1.5pt} q}$-linear morphism that induces an isomorphism of the tangent spaces at zero. Let $V$ be the kernel of $\varphi$ viewed as a morphism of sheaves on the small étale site of $\operatorname {Spec} K$. The sheaf $V$ corresponds to the $\mathbf {F}_{\hspace {-1.5pt} q}$-vector space of roots

\[ \{ y \in E(K^s), \:\varphi(y) = 0 \} \]

equipped with the natural Galois action. The short exact sequence of sheaves

induces a long exact sequence of cohomology that terminates in a surjective boundary homomorphism

The boundary homomorphism $\partial _\varphi$ sends $x \in E(K)$ to the class of the cocycle $g \mapsto g y - y$ with $y \in E(K^s)$ any element satisfying $\varphi (y) = x$.

We will refer to $\partial _\varphi$ as the Artin–Schreier homomorphism of the isogeny $\varphi$. We will use the shorthand $\partial _q$ to denote the Artin–Schreier homomorphism of the isogeny $\tau - 1\colon \mathbf {G}_a \to \mathbf {G}_a$ with kernel the constant sheaf $\mathbf {F}_{\hspace {-1.5pt} q}$.

Suppose that the sheaf $V$ is constant or, equivalently, that the $\mathbf {F}_{\hspace {-1.5pt} q}$-vector space $V$ is contained in $E(K)$. Then the cohomology group $H^1(K,\:V)$ coincides with the $\mathbf {F}_{\hspace {-1.5pt} q}$-vector space of continuous homomorphisms $G_K\to V$. In this case, we will often write the Artin–Schreier boundary homomorphism $\partial _\varphi$ in the form of a pairing

\[ [\ ,\ )_{\varphi}\colon E(K) \times G_K \to V, \quad [x,\ )_{\varphi} = \partial_{\varphi}(x). \]

We will use the shorthand $[\ ,\ )_{q}$ for the pairing of the isogeny $\tau -1$.

Lemma 2.2.1 Let $\varphi \colon \mathbf {G}_a \to \mathbf {G}_a$ be a separable isogeny with kernel $V$. Then for every Galois-equivariant epimorphism $f\colon V \twoheadrightarrow \mathbf {F}_{\hspace {-1.5pt} q}$, there is a scaling factor $u \in K$ which makes the following square commutative.

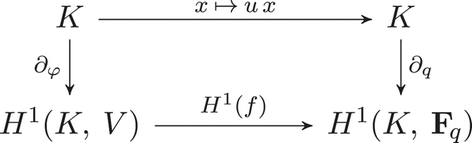
The factor $u$ is computed via Moore determinants:

\[ u = \alpha^{-1} \biggl(\frac{M(w_1,\dotsc,w_n)}{M(w_1,\dotsc,w_n,v)}\biggr)^q.\]

The terms in this formula have the following meaning:

• – $\alpha$ is the top coefficient of the $\tau$-polynomial $\varphi$;

• – $v \in V$ is an element such that $f(v) = 1$;

• – $w_1, \dotsc, w_n \in V$ is a basis of the hyperplane $\ker (f) \subset V$.

The value of $u$ is independent of choices of $v$ and $w_1,\dotsc,w_n$.

The factor $u$ of Lemma 2.2.1 is unique provided that $H^1(K,\,\mathbf {F}_{\hspace {-1.5pt} p}) \ne 0$.

Proof of Lemma 2.2.1 As a first step we shall prolong the morphism $f\colon V \to \mathbf {F}_{\hspace {-1.5pt} q}$ to the following morphism of short exact sequences of sheaves.

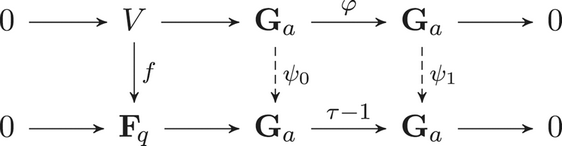
By Lemma 2.1.1(1) there is a unique polynomial $\psi _0 \in K[\tau ]$ of degree strictly less than $\dim V = n + 1$ which makes the left square commutative. The composite $(\tau - 1) \psi _0$ vanishes on the $\mathbf {F}_{\hspace {-1.5pt} q}$-vector subspace $V \subset K^s$, and is thus divisible by the polynomial $\varphi$ on the right [Pap23, Corollary 3.1.16]. We get the existence of the polynomial $\psi _1$. By construction, $\deg \psi _0 \leqslant n$ and $\deg \varphi = n+1$ so the relation

\[ \psi_1 \varphi = (\tau - 1)\psi_0 \]

implies that the polynomial $\psi _1 = u$ is constant, and that

\[ u \alpha = \beta^q, \]

where the element $\beta$ is the top coefficient of the polynomial $\psi _0$. This coefficient is computed by Lemma 2.1.1(2) which yields the Moore determinant formula for $u$.

2.3 Drinfeld modules

Fix a global function field $F$ over $\mathbf {F}_{\hspace {-1.5pt} q}$ and a place $\infty$ of $F$. As in § 1.2 this determines a coefficient ring $A$, i.e. the subring of $F$ consisting of elements which are regular outside $\infty$. We will freely use the notation and the terminology of § 1.2 with respect to coefficient rings and related objects.

For us a Drinfeld $A$-module over $\operatorname {Spec} K$ is an $A$-module scheme $E$ such that the underlying $\mathbf {F}_{\hspace {-1.5pt} q}$-module scheme is isomorphic to $\mathbf {G}_a$, and the multiplication morphism $a\colon E \to E$ is an isogeny of degree strictly greater than $1$ for at least one element $a \in A$.

Subject to a choice of an $\mathbf {F}_{\hspace {-1.5pt} q}$-linear isomorphism $E \xrightarrow {\smash {{ {\sim }}}} \mathbf {G}_a$ the data of an $A$-module structure on $E$ amounts to a morphism of $\mathbf {F}_{\hspace {-1.5pt} q}$-algebras $\varphi \colon A \to K[\tau ]$, and one recovers the more common definition of a Drinfeld module.

Let $\operatorname {Lie}_E$ be the tangent space of $E$ at zero. This is a vector space of dimension $1$ over the base field $K$. The action of $A$ on $\operatorname {Lie}_E$ determines a morphism $\iota _E\colon A \to K$, the characteristic homomorphism of the Drinfeld module $E$. The characteristic of $E$ is the ideal $\ker (\iota _E) \subset A$.

Let $\mathfrak {n} \subset A$ be a proper ideal which is not divisible by the characteristic of $E$. The $\mathfrak {n}$-torsion of $E$ is most naturally represented by the $A/\mathfrak {n}$-module

\[ E[\mathfrak{n}] = \operatorname{Hom}_A(A/\mathfrak{n}, E(K^s)). \]

We will use a modified definition which makes it easier to form inverse systems.

Definition 2.3.1 We have $E[\mathfrak {n}\rangle = \operatorname {Hom}_A(\mathfrak {n}^{-1}/A, E(K^s))$.

The $A/\mathfrak {n}$-module $E[\mathfrak {n}\rangle$ inherits an action of the absolute Galois group $G_K$ from $E(K^s)$. As the $A/\mathfrak {n}$-module $\mathfrak {n}^{-1}/A$ is free of rank $1$ a choice of its generator gives rise to a $G_K$-equivariant isomorphism of $A/\mathfrak {n}$-modules:

\[ E[\mathfrak{n}\rangle \xrightarrow{\smash{{{\sim}}}} E[\mathfrak{n}]. \]

An inclusion of ideals $\mathfrak {n}'\subset \mathfrak {n}$ induces a surjection $E[\mathfrak {n}'\rangle \twoheadrightarrow E[\mathfrak {n}\rangle$, and the resulting morphism $A/\mathfrak {n} \otimes _{A/\mathfrak {n}'} E[\mathfrak {n}'\rangle \xrightarrow {\smash {{ {\sim }}}} E[\mathfrak {n}\rangle$ is an isomorphism.

Lemma 2.3.2 We have a Galois-equivariant short exact sequence of $A$-modules which is natural in the ideal $\mathfrak {n}$ and the Drinfeld module $E$:

The first arrow is given by the composition with the quotient map $\mathfrak {n}^{-1} \twoheadrightarrow \mathfrak {n}^{-1}/A$ and the second arrow is the evaluation at $1 \in \mathfrak {n}^{-1}$.

Proof. We only need to prove the exactness on the right. Suppose that $\mathfrak {n} = (a)$ for some $a \in A$. The isogeny $a\colon E \to E$ is separable since the ideal $\mathfrak {n}$ is not divisible by the characteristic of $E$. Hence, the morphism $a\colon E(K^s) \twoheadrightarrow E(K^s)$ is surjective, and we get the claim.

In the general case the ideal $\mathfrak {n}^i$ is principal for all sufficiently divisible integers $i > 0$ since the Picard group of the scheme $\operatorname {Spec} A$ is finite. The claim results from the naturality of our sequence with respect to the ideal $\mathfrak {n}$.

Definition 2.3.3 The Kummer boundary homomorphism

\[ \partial_{\mathfrak{n}}\colon E(K) \to H^1(K,\:E[\mathfrak{n}\rangle) \]

is the boundary homomorphism arising from the sequence of Lemma 2.3.2. When the $\mathfrak {n}$-torsion of $E$ is rational we will write it in the form of a pairing:

\[ [\ ,\ )_{\mathfrak{n}}\colon E(K) \times G_K \to E[\mathfrak{n}\rangle. \]

The map $\partial _{\mathfrak {n}}$ can be also called the Artin–Schreier homomorphism but this name is less common in the literature.

Lemma 2.3.4 The homomorphism $\partial _{\mathfrak {n}}$ has the following description:

1. (1) For each $x \in E(K)$ there is an $A$-module homomorphism $f\colon \mathfrak {n}^{-1} \to E(K^s)$ such that $f(1) = x$.

2. (2) The cohomology class $\partial _{\mathfrak {n}}(x)$ is represented by a cocycle given by the formula $g \mapsto g \circ f - f$ where the right-hand side is seen as a morphism from the quotient $\mathfrak {n}^{-1}/A$.

Proof. This follows from Lemma 2.3.2 by elementary properties of group cohomology.

Lemma 2.3.5 For each proper principal ideal $(a) = \mathfrak {a}$ of the ring $A$ which is not divisible by the characteristic of $E$ we have a commutative diagram

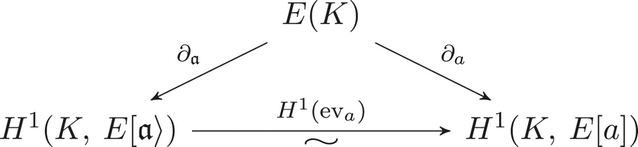
where $\partial _{a}$ is the Artin–Schreier boundary homomorphism of the separable isogeny $a\colon E \to E$, and $\text {ev}_{a}\colon E[\mathfrak {a}\rangle \xrightarrow {\smash {{ {\sim }}}} E[a]$ is an isomorphism defined by the formula $x\mapsto x(a^{-1})$.

Proof. We have the following commutative diagram.

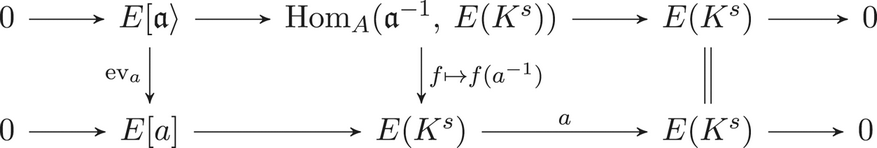
The claim follows by naturality of boundary homomorphisms.

2.4 Drinfeld modules over local fields

In this section our base field $K$ is assumed to be local. We denote by $\mathcal {O}_K$ the ring of integers of $K$ and by $\mathfrak {p}_K$ the maximal ideal of $\mathcal {O}_K$.

Pick a coefficient ring $A$ over $\mathbf {F}_{\hspace {-1.5pt} q}$. Let $E$ be a Drinfeld $A$-module over $\operatorname {Spec} K$ and let $\iota _E\colon A \to K$ be its characteristic homomorphism.

Definition 2.4.1 The Drinfeld module $E$ has finite residual characteristic when $\iota _E(A) \subset \mathcal {O}_K$. The residual characteristic $\bar {\mathfrak {p}}$ of $E$ is the ideal

\[ \bar{\mathfrak{p}} := \iota_E^{-1}(\mathfrak{p}_K). \]

This ideal is maximal because the residue field $\mathcal {O}_K/\mathfrak {p}_K$ is finite.

The analogous situation for abelian varieties is when the base field $K$ is a non-archimedean local field. The residual characteristic of an abelian variety is just the residual characteristic of the field $K$.

From now on we suppose that the Drinfeld module $E$ has finite residual characteristic. It will be convenient for us to assemble the $\mathfrak {p}$-adic Tate modules $T_\mathfrak {p} E$, $\mathfrak {p}\ne \bar {\mathfrak {p}}$, into a single object.

Definition 2.4.2 The ring of restricted integral adeles is defined by the formula

\[ {A}_{\text{ad},\bar{\mathfrak{p}}} = \varprojlim\nolimits_{\mathfrak{n}} A/\mathfrak{n}, \]

where $\mathfrak {n} \subset A$ runs over proper ideals that are prime to $\bar {\mathfrak {p}}$.

We have a natural isomorphism ${A}_{\text {ad},\bar {\mathfrak {p}}} = \prod _{\mathfrak {p}\ne \bar {\mathfrak {p}}} A_\mathfrak {p}$ where $A_\mathfrak {p}$ is the $\mathfrak {p}$-adic completion of $A$. Compared with the ring of integral adeles of the function field $F$, the ring ${A}_{\text {ad},\bar {\mathfrak {p}}}$ does not include the factors at the places $\bar {\mathfrak {p}}$ and $\infty$.

Definition 2.4.3 The restricted adelic Tate module ${T}_{\text {ad},\bar {\mathfrak {p}}} E$ is defined by the formula

\[ {T}_{\text{ad},\bar{\mathfrak{p}}} E = \varprojlim\nolimits_{\mathfrak{n}} E[\mathfrak{n}\rangle, \]

where $\mathfrak {n} \subset A$ runs over proper ideals that are prime to $\bar {\mathfrak {p}}$ and the transition maps are induced by inclusions of the ideals.

The Tate module ${T}_{\text {ad},\bar {\mathfrak {p}}} E$ is a free module over the ring ${A}_{\text {ad},\bar {\mathfrak {p}}}$ and its rank coincides with the rank of the Drinfeld module $E$. The Galois action on ${T}_{\text {ad},\bar {\mathfrak {p}}} E$ is ${A}_{\text {ad},\bar {\mathfrak {p}}}$-linear. We have a natural ${A}_{\text {ad},\bar {\mathfrak {p}}}$-linear Galois-equivariant isomorphism:

\[ {T}_{\text{ad},\bar{\mathfrak{p}}} E \xrightarrow{\smash{{{\sim}}}} \prod\nolimits_{\mathfrak{p}\ne\bar{\mathfrak{p}}} T_\mathfrak{p} E. \]

Lemma 2.4.4 Consider the inclusion-ordered family $\mathcal {F}$ of proper principal ideals $\mathfrak {a} \subset A$ that are prime to the residual characteristic $\bar {\mathfrak {p}}$. Then the natural homomorphism

\[ {T}_{\text{ad},\bar{\mathfrak{p}}} E \xrightarrow{\smash{{{\sim}}}} \varprojlim\nolimits_{\mathfrak{a} \in \mathcal{F}} E[\mathfrak{a}\rangle \]

is an isomorphism.

Proof. For each proper ideal $\mathfrak {n}\not \subset \bar {\mathfrak {p}}$ there is a non-constant element $a \in \mathfrak {n} \smallsetminus \bar {\mathfrak {p}}$. Then $(a) \in \mathcal {F}$, and as $(a) \subset \mathfrak {n}$ we conclude that the family $\mathcal {F}$ is initial in the family of all proper ideals not contained in $\bar {\mathfrak {p}}$. The claim follows.

3. The local Kummer pairing

Fix a finite field $\mathbf {F}_{\hspace {-1.5pt} q}$ of cardinality $q$ and characteristic $p$. In this section our base field $K/\mathbf {F}_{\hspace {-1.5pt} q}$ is assumed to be local. We denote by $\mathcal {O}_K\subset K$ the ring of integers and by $\mathfrak {p}_K \subset \mathcal {O}_K$ the maximal ideal. As usual we fix a separable closure $K^s/K$ and denote by $G_K$ the corresponding absolute Galois group.

3.1 Ramification subgroups

Let $I_K$ be the inertia subgroup of the absolute Galois group $G_K$, and let $P_K$ be the wild inertia subgroup.

Definition 3.1.1 We denote by $J_K$ the maximal quotient of $I_K$ that is abelian of exponent $p$:

\[ J_K := I_K^{\text{ab}}/(I_K^{\text{ab}})^{\times p}. \]

The quotient group $I_K/P_K$ is procyclic of order prime to $p$, so the fact that $P_K$ is a pro-$p$ group implies that the surjection $I_K \twoheadrightarrow I_K/P_K$ is split. As the group $J_K$ is abelian $p$-torsion we conclude that the canonical morphism $P_K \twoheadrightarrow J_K$ is surjective.

The inertia subgroup $I_K$ carries a decreasing separated exhaustive filtration by closed normal subgroups $I_K^{u}$, $u \in \mathbf {Q}_{\geqslant 0}$, the ramification filtration in upper numbering [Ser68, Chapitre IV, § 3, Remarque 1, p. 83]. The wild inertia subgroup $P_K$ is the closure of the subgroup $\bigcup _{u > 0} I_K^{u}$.

The ramification filtration of $I_K$ induces a filtration of $J_K$. As the group $J_K$ is abelian the Hasse–Arf theorem implies that the induced filtration is integrally indexed: for each $u\geqslant 0$ the subgroup $J_K^u$ coincides with $J_K^m$, $m = \lceil u \rceil$.

Lemma 3.1.2 For every integer $m \geqslant 0$ such that $m \equiv 0\pmod {p}$ we have

\[ J_K^m = J_K^{m+1}. \]

Proof. Let $L\subset K^s$ be a finite Galois extension of $K$ with Galois group $G$ and upper index ramification filtration $\{ G^u \}_{u\geqslant 0}$. Suppose that the inertia group $G^0$ is abelian $p$-torsion. We need to show that $G^{pi} = G^{pi+1}$ for each $i \geqslant 0$.

We are free to assume that $\smash {G^0} = G$. The group $G$ is abelian, so we have the reciprocity morphism $\omega \colon K^\times \twoheadrightarrow G$ of local class field theory. This morphism transforms the $n$-unit filtration $\smash {\{U_K^{(n)}\}_{n\geqslant 0}}$ to the ramification filtration. For each $i \geqslant 0$ the $p$th power map induces a morphism

\[ U_K^{(i)} \twoheadrightarrow U_K^{(pi)}/U_K^{(pi+1)}. \]

This is surjective since the residue field of $K$ is perfect. Our claim follows.

3.2 Local pairing

Fix a Drinfeld $A$-module ${D}$ over $\operatorname {Spec} \mathcal {O}_K$. By this we mean not only that ${D}$ can be defined by a homomorphism $\varphi \colon A \to \mathcal {O}_K[\tau ]$ but also that the reduction of $\varphi$ modulo $\mathfrak {p}_K$ is a Drinfeld module of the same rank as over $K$.

The Drinfeld module ${D}$ has finite residual characteristic, denoted by $\bar {\mathfrak {p}}$ as usual. Let $K^\textit {ur}\subset K^s$ be the maximal unramified extension and let $\mathfrak {n}\subset A$ be a proper ideal not divisible by $\bar {\mathfrak {p}}$. Since ${D}$ is a Drinfeld module over $\operatorname {Spec}\mathcal {O}_K$ the $\mathfrak {n}$-torsion of ${D}$ is contained in ${D}(K^\textit {ur})$. Hence, by § 2.3 we have the Kummer pairing $[\ ,\ )_{\mathfrak {n}}\colon {D}(K^\textit {ur}) \times I_K \to {D}[\mathfrak {n}\rangle$.

Definition 3.2.1 The local restricted adelic Kummer pairing

\[ [\ ,\ )_{\text{ad}}\colon {D}(K^\textit{ur}) \times I_K \to {T}_{\text{ad},\bar{\mathfrak{p}}} {D} \]

is the limit of the Kummer pairings $[\ ,\ )_{\mathfrak {n}}$ over the inclusion-ordered system of proper ideals $\mathfrak {n}$ not divisible by the residual characteristic $\bar {\mathfrak {p}}$.

Since the Tate module ${T}_{\text {ad},\bar {\mathfrak {p}}}{D}$ is $p$-torsion the pairing $[\ ,\ )_{\text {ad}}$ factors through the maximal quotient $J_K = I_K^{\text {ab}}/(I_K^{\text {ab}})^{\times p}$ that is abelian of exponent $p$.

Let $v\colon K \twoheadrightarrow \mathbf {Z} \cup \{\infty \}$ be the normalized valuation of the base field $K$. Every isomorphism of $\mathbf {F}_{\hspace {-1.5pt} q}$-module schemes ${D} \xrightarrow {\smash {{ {\sim }}}} \mathbf {G}_a$ over $\operatorname {Spec} \mathcal {O}_K$ induces a valuation function on ${D}(K)$ by transport of structure from $\mathbf {G}_a(K) = K$. The result is independent of choices because the choices differ by multiplication by an integral unit on the side of $\mathbf {G}_a$. We denote the resulting valuation function by $v$ as well.

Definition 3.2.2 For every $\lambda \in {D}(K)$ we set

\[ \|\lambda\| = \max\{0, \:-v(\lambda)\}. \]

Poonen [Poo95] introduced the notion of canonical local height on the $A$-module ${D}(K)$. Since the Drinfeld module ${D}$ has good reduction, Proposition 4(4) of [Poo95, § 3] implies that the map $\|\cdot \|\colon {D}(K) \to \mathbf {Z}_{\geqslant 0}$ is exactly the canonical local height. This map satisfies the ultrametric inequality:

\[ \|\lambda + \lambda'\| \leqslant \max\{ \|\lambda\|, \|\lambda'\| \}. \]

However, $\|\lambda \| = 0$ for every $\lambda \in {D}(\mathcal {O}_K)$ so the height $\|\cdot \|$ is only a seminorm on ${D}(K)$. This seminorm is $\infty$-adic in the following sense.

Lemma 3.2.3 For each $\lambda \in {D}(K)$ and each $a \in A$ we have an equality

\[ \|a\lambda\| = |a|_\infty^s \, \|\lambda\|, \]

where $s$ is the rank of the Drinfeld module ${D}$.

The map $x \mapsto |x|_\infty ^s$ is an $\infty$-adic absolute value on the local field $F_\infty$ albeit its normalization differs from the one of § 1.2 when $s > 1$.

Proof of Lemma 3.2.3 This follows from Proposition 2 and Proposition 4(4) of [Poo95]. For the reader's convenience let us give a direct argument. The claim is clear when $a = 0$ and holds when $\|\lambda \| = 0$ since ${D}(\mathcal {O}_K)$ is an $A$-submodule of ${D}(K)$. We are thus free to assume that $a \ne 0$ and $\|\lambda \| > 0$.

We identify the $\mathbf {F}_{\hspace {-1.5pt} q}$-module scheme ${D}$ with $\mathbf {G}_a$ over $\operatorname {Spec} \mathcal {O}_K$. The induced $A$-module scheme structure is described by a homomorphism $\varphi \colon A \to \mathcal {O}_K[\tau ]$. Write $\varphi (a) = \alpha _0 + \alpha _1 \tau + \dotsb + \alpha _n \tau ^n$ with $\alpha _n \ne 0$. The top coefficient $\alpha _n$ is a unit since ${D}$ is a Drinfeld module over $\operatorname {Spec} \mathcal {O}_K$. Hence, $v(\alpha _n \lambda ^{q^n}) = q^n v(\lambda )$. Combining this with the estimates $v(\alpha _i \lambda ^{q^i}) \geqslant q^i v(\lambda )$, $i < n$, and the assumption $v(\lambda ) < 0$ we deduce an equality

\[ v(a \, \lambda) = q^n \, v(\lambda). \]

The degree $n$ of the polynomial $\varphi (a)$ is expressed by a formula

\[ n = -s \, [\kappa_\infty:\mathbf {F}_{\hspace{-1.5pt} q}] \, v_\infty(a), \]

where $v_\infty$ is the normalized valuation of the local field $F_\infty$. The absolute value of § 1.2 is given by the formula

\[ |a|_\infty = |\kappa_\infty|^{-v_\infty(a)}. \]

As $|\kappa _\infty | = q^{[\kappa _\infty :\mathbf {F}_{\hspace {-1.5pt} q}]}$ we deduce that $q^n = |a|_\infty ^s$ and the claim follows.

Theorem 3.2.4 Let $\lambda \in {D}(K)$ be an element, and consider the homomorphism

\[ [\lambda,\ )_{\text{ad}}\colon J_K \to {T}_{\text{ad},\bar{\mathfrak{p}}} {D}. \]

Then the following hold.

1. (1) This homomorphism vanishes on the ramification subgroup $J^{\|\lambda \|+1}_K$. In particular, it vanishes altogether when $\|\lambda \| = 0$.

2. (2) If the height $\|\lambda \|$ is prime to $p$, then the homomorphism $[\lambda,\ )_{\text {ad}}$ maps the ramification subgroup $\smash {J^{\|\lambda \|}_K}$ surjectively onto ${T}_{\text {ad},\bar {\mathfrak {p}}} {D}$.

Proof. By Lemmas 2.4.4 and 2.3.5 it is enough to prove the claims for every homomorphism $[\lambda,\ )_{a}\colon J_K \to {D}[a]$ where $a \in A$ runs over non-constant elements that are prime to the residual characteristic $\bar {\mathfrak {p}}$ of ${D}$.

The height $\|\lambda \|$, the group $J_K$ and the homomorphism $[\lambda,\ )_{a}$ remain unchanged when we replace the base field $K$ by an unramified extension. As the Drinfeld module ${D}$ has good reduction and the element $a$ is prime to $\bar {\mathfrak {p}}$ we are free to assume that the torsion module ${D}[a]$ is contained in ${D}(K)$, and consequently in ${D}(\mathcal {O}_K)$.

An $\mathbf {F}_{\hspace {-1.5pt} p}$-vector subspace $V\subset {D}[a]$ is zero if and only if $f(V) = 0$ for each nonzero linear form $f\colon {D}[a] \twoheadrightarrow \mathbf {F}_{\hspace {-1.5pt} p}$. Likewise $V = {D}[a]$ if and only if $f(V) = \mathbf {F}_{\hspace {-1.5pt} p}$ for every such form $f$. It is thus enough to prove our claims after composing the homomorphism $[\lambda,\ )_{a}$ with every $f$.

From now on we identify the $\mathbf {F}_{\hspace {-1.5pt} q}$-module scheme ${D}$ with $\mathbf {G}_a$ over $\operatorname {Spec} \mathcal {O}_K$. The resulting $A$-module scheme structure on $\mathbf {G}_a$ is given by a homomorphism $\varphi \colon A \to \mathcal {O}_K[\tau ]$.

Let $f\colon {D}[a] \twoheadrightarrow \mathbf {F}_{\hspace {-1.5pt} p}$ be a nonzero linear form. According to Lemma 2.2.1 there is an element $u \in \mathbf {G}_a(K)$ such that

\[ f \circ [\lambda,\ )_{\varphi(a)} = [u\lambda,\ )_{p}. \]

This element is given by a formula with Moore determinants $M(-)$:

\[ u = \alpha^{-1}\biggl( \frac{M(w_1,\dotsc,w_n)}{M(w_1,\dotsc,w_n,v)}\biggr)^p. \]

Here $\alpha$ is the top coefficient of the polynomial $\varphi (a)$ and $w_1, \dotsc,w_n,v$ is a suitable $\mathbf {F}_{\hspace {-1.5pt} p}$-basis of ${D}[a]$.

By our assumption ${D}$ is a Drinfeld module over $\operatorname {Spec}\mathcal {O}_K$. This implies that the top coefficient $\alpha$ is an integral unit. Since $a$ is prime to the residual characteristic the torsion module ${D}[a] \subset {D}(\mathcal {O}_K)$ maps injectively to ${D}(k)$ where $k$ is the residue field of $\mathcal {O}_K$. In particular, the image of the basis $w_1,\dotsc,w_n,v$ in ${D}(k)$ remains $\mathbf {F}_{\hspace {-1.5pt} p}$-linearly independent. Hence, the corresponding Moore determinants are nonzero. We conclude that the element $u$ is an integral unit. It follows that $v(u\lambda ) = v(\lambda )$.

Consider the Artin–Schreier polynomial $X^p - X = u\lambda$. The Galois group $G$ of its splitting field is the image of the absolute Galois group under the homomorphism $[u\lambda,\ )_{p}$. The upper index ramification filtration of $G$ is given by images of absolute ramification subgroups:

\[ G^{i} = [u\lambda, I_K^{i})_{p}. \]

This filtration was calculated by Hasse (see Thomas [Tho05], Proposition 2.1 and the following paragraph). Set $b = \max \{0,\,-v(u\lambda )\}$. Then the subgroups $G^{i}$ vanish for $i > b$, and if the integer $b$ is prime to $p$, then $G^{b} = G = \mathbf {F}_{\hspace {-1.5pt} p}$. Our theorem follows since $v(u\lambda ) = v(\lambda )$ as shown previously.

3.3 Open image theorem

The following arguments involve passage from the base field $K$ to a finite separable extension $L$. On account of this we have to fix a few conventions. First, it will be more convenient for us to view the homomorphism $[\lambda,\ )_{\text {ad}}$ as a morphism from the inertia subgroup $I_K$ rather than its quotient $J_K$.

Second, we need to be careful with the canonical local height on the $A$-module ${D}(L)$. This involves the normalized valuation of $L$ and so differs from the height on the submodule ${D}(K)$ by an integer factor, the ramification index of $L/K$. We will denote the height on ${D}(L)$ by $\|\cdot \|_{L}$.

Lemma 3.3.1 Let $\lambda \in {D}(K) \smallsetminus {D}(\mathcal {O}_K)$ be an element, and suppose that the homomorphism $[\lambda,\ )_{\text {ad}}\colon I_K \to {T}_{\text {ad},\bar {\mathfrak {p}}} {D}$ is not surjective. Then there are:

• – a non-constant element $a \in A$ prime to the residual characteristic $\bar {\mathfrak {p}}$ of ${D}$;

• – a finite separable extension $L/K$; and

• – an element $\lambda ' \in {D}(L)\smallsetminus {D}(\mathcal {O}_L)$;

such that

\[ a \lambda' = \lambda, \quad v_p(\|\lambda'\|_{L}) < v_p(\|\lambda\|_{K}). \]

Here $v_p\colon \mathbf {Q} \twoheadrightarrow \mathbf {Z}\cup \{\infty \}$ denotes the normalized $p$-adic valuation.

Proof. Lemmas 2.4.4 and 2.3.5 imply that there is a non-constant element $a \not \in \bar {\mathfrak {p}}$ such that the homomorphism $[\lambda,\ )_{a}\colon I_K \to {D}[a]$ is not surjective.

The height $\|\lambda \|$, the inertia group $I_K$ and the homomorphism $[\lambda,\ )_{a}$ remain unchanged when we replace the base field $K$ by an unramified extension. We are thus free to assume that the torsion scheme ${D}[a]$ is constant or, in other words, that all the $K^s$-points of ${D}[a]$ are defined over the field $K$. Under this assumption the homomorphism $[\lambda,\ )_{a}$ is defined on the absolute Galois group $G_K$, see § 2.2. Its kernel determines a finite abelian $p$-torsion extension $L/K$.

Let $I \subset {D}[a]$ be the image of the inertia subgroup $I_K$. The ramification index $e$ of the extension $L/K$ equals the cardinality of $I$. By our choice of the absolute value $|\cdot |_\infty$ in § 1.2 we have an equality $|A/(a)| = |a|_\infty$. Thus, the torsion module ${D}[a]$ has cardinality $|a|_\infty ^s$, and the assumption $I \ne {D}[a]$ implies that $e < |a|_\infty ^s$.

By construction there is an element $\lambda ' \in {D}(L)$ such that $a \lambda ' = \lambda$. We have $\|\lambda \|_{L} = e \, \|\lambda \|_{K}$ so Lemma 3.2.3 shows that

\[ |a|_\infty^s \, \|\lambda'\|_{L} = e \, \|\lambda\|_{K}. \]

The integers $e$ and $|a|_\infty$ are powers of $p$ so the strict inequality $e < |a|_\infty ^s$ implies a strict inequality of $p$-adic valuations $v_p(\|\lambda '\|_{L}) < v_p(\|\lambda \|_{K})$ as claimed.

Theorem 3.3.2 For each element $\lambda \in {D}(K) \smallsetminus {D}(\mathcal {O}_K)$ the homomorphism $[\lambda,\ )_{\text {ad}}\colon I_K \to {T}_{\text {ad},\bar {\mathfrak {p}}} {D}$ has open image.

Proof. Suppose that the homomorphism is not surjective. Invoking Lemma 3.3.1 we obtain a non-constant element $a \in A\smallsetminus \bar {\mathfrak {p}}$, a finite separable extension $L/K$ and an element $\lambda ' \in {D}(L)$ such that $a \lambda ' = \lambda$. As the pairing $[\ ,\ )_{\text {ad}}$ is $A$-linear in the first argument we deduce that

\[ a [\lambda', I_L)_{\text{ad}} = [\lambda, I_L)_{\text{ad}}. \]

The right-hand side has finite index in $[\lambda, I_K)_{\text {ad}}$. Hence, it is enough to prove the theorem with $\lambda$ replaced by $\lambda '$ and $K$ replaced by $L$.

Lemma 3.3.1 also shows that we have a strict inequality of $p$-adic valuations:

\[ v_p(\|\lambda'\|_{L}) < v_p(\|\lambda\|_{K}). \]

The height $\|\cdot \|_{L}$ takes only integer values, so the valuation $v_p(\|\lambda '\|_{L})$ is bounded below by zero. Hence, after repeating our argument finitely many times we arrive at a situation where the homomorphism $[\lambda ',\ )_{\text {ad}}$ is onto.

4. Applications

We retain the notation and the conventions of § 3. In particular, our base field $K$ is a local field over a finite field $\mathbf {F}_{\hspace {-1.5pt} q}$ of cardinality $q$ and characteristic $p$. We fix a separable closure $K^s/K$, denote by $G_K$ the corresponding absolute Galois group, by $I_K$ the inertia subgroup and by $J_K$ the maximal quotient of $I_K$ that is abelian of exponent $p$; see § 3.1

4.1 The conductor of a Drinfeld module

Let $A$ be a coefficient ring over $\mathbf {F}_{\hspace {-1.5pt} q}$ and let $E$ be a Drinfeld $A$-module of stable reduction over $\operatorname {Spec} K$. Drinfeld's theory of Tate uniformization [Dri74, § 7] represents $E$ as an analytic quotient of a Drinfeld module ${D}$ over $\operatorname {Spec}\mathcal {O}_K$ by a Galois-invariant lattice $\varLambda \subset {D}(K^s)$, a finitely generated projective $A$-submodule which is discrete with respect to the adic topology. We thus have an analytic morphism $e_\varLambda \colon {D} \to E$ extending to a short exact sequence:

This sequence is determined functorially by the Drinfeld module $E$. We will refer to $\varLambda$ as the period lattice of $E$ and to $e_\varLambda$ as the exponential map of $\varLambda$. A detailed exposition of Tate uniformization theory can be found in a recent book by Papikian [Pap23, § 6.2].

Throughout this section we make an additional assumption: the lattice $\varLambda$ is defined over $K$, which is to say, $\varLambda \subset {D}(K)$. We will study the action of inertia on the Tate modules of $E$.

Lemma 4.1.1 The Drinfeld modules ${D}$ and $E$ have the same characteristic homomorphism.

Proof. The proof follows since the exponential $e_\varLambda$ induces an isomorphism of tangent spaces $\operatorname {Lie}_{D} \xrightarrow {\smash {{ {\sim }}}} \operatorname {Lie}_E$.

Lemma 4.1.2 For each proper ideal $\mathfrak {n}\subset A$ that is not divisible by the characteristic of $E$ we have a Galois-equivariant short exact sequence of $A/\mathfrak {n}$-modules:

The homomorphism $\delta _{\mathfrak {n}}$ has the following description.

1. (1) For each $x \in E[\mathfrak {n}\rangle$ there is an $A$-module morphism $\tilde {x}\colon \mathfrak {n}^{-1} \to {D}(K^s)$ which lifts $x$ in the sense that $e_\varLambda \circ \tilde {x}$ equals the composite of $x$ and the quotient morphism $\mathfrak {n}^{-1} \twoheadrightarrow \mathfrak {n}^{-1}/A$.

2. (2) The residue class $\delta _{\mathfrak {n}}(x)$ is represented by the element $\tilde {x}(1) \in \varLambda$ where $\tilde {x}$ is a lift of $x$.

3. (3) Given a representative $\lambda$ of the residue class $\delta _{\mathfrak {n}}(x)$ one can pick a lift $\tilde {x}$ such that $\tilde {x}(1) = \lambda$.

Proof. Consider a commutative diagram

with the vertical arrows given by $A$-module multiplication. The bottom row of this diagram is exact by construction and the top row is exact since the $A$-module $\mathfrak {n}$ is flat.

Consider the natural isomorphism $\mathfrak {n}\otimes _A M \xrightarrow {\smash {{ {\sim }}}} \operatorname {Hom}_A(\mathfrak {n}^{-1},\:M)$. Under this isomorphism the multiplication map $\mathfrak {n} \otimes _A M \to M$ is transformed to the evaluation map $f \mapsto f(1)$. Hence, the middle vertical arrow in the diagram above is surjective by Lemma 2.3.2, and our claims follow from the snake lemma.

Lemma 4.1.1 implies that Drinfeld modules ${D}$ and $E$ have the same residual characteristic. As usual, we denote this characteristic by $\bar {\mathfrak {p}}$. Consider the restricted adelic Tate module ${T}_{\text {ad},\bar {\mathfrak {p}}} E$ and let $\operatorname {GL}({T}_{\text {ad},\bar {\mathfrak {p}}} E)$ be the group of its automorphisms as an ${A}_{\text {ad},\bar {\mathfrak {p}}}$-module. The action of the inertia subgroup $I_K$ gives rise to the (local) restricted adelic monodromy representation

\[ \rho\colon I_K \to \operatorname{GL}({T}_{\text{ad},\bar{\mathfrak{p}}} E). \]

Similarly, for each prime $\mathfrak {p}\ne \bar {\mathfrak {p}}$ we have the $\mathfrak {p}$-adic monodromy representation $\rho _{\mathfrak {p}}\colon I_K \to \operatorname {GL}(T_\mathfrak {p} E)$. The representation $\rho _{\mathfrak {p}}$ is the composite of $\rho$ and the projection $\operatorname {GL}({T}_{\text {ad},\bar {\mathfrak {p}}} E) \to \operatorname {GL}(T_\mathfrak {p} E)$.

Taking the limit of sequences of Lemma 4.1.2 we obtain a short exact sequence of Galois representations:

As the Drinfeld module ${D}$ has good reduction we have at our disposal the local adelic Kummer pairing

\[ [\ ,\ )_{\text{ad}}\colon {D}(K) \times I_K \to {T}_{\text{ad},\bar{\mathfrak{p}}}{D}. \]

Lemma 4.1.3 The monodromy representation $\rho$ factors as a composition

where the second arrow is given by the formula $f \mapsto 1 + {T}_{\text {ad},\bar {\mathfrak {p}}}(e_\varLambda ) \circ f \circ \delta _{\text {ad}}$.

Proof. Let $\mathfrak {n} \subset A$ be a proper ideal not divisible by $\bar {\mathfrak {p}}$ and let $x \in E[\mathfrak {n}\rangle$ be an element. Pick a representative $\lambda$ of the residue class $\delta _{\mathfrak {n}}(x)$. We need to show that for each automorphism $g \in I_K$ one has

\[ g \circ x = x + e_\varLambda \circ [\lambda, g)_{\mathfrak{n}}. \]

Let $\tilde {x}\colon \mathfrak {n}^{-1} \to {D}(K^s)$ be a lift of $x$. By Lemma 4.1.2(3) we are free to assume that $\tilde {x}(1) = \lambda$. Lemma 2.3.4 shows that

\[ [\lambda, g)_{\mathfrak{n}} = g \circ \tilde{x} - \tilde{x}. \]

Hence, $e_\varLambda \circ [\lambda, g)_{\mathfrak {n}} = g \circ x - x$, and we are done.

Corollary 4.1.4 The monodromy representation $\rho$ factors through the maximal quotient $J_K = I_K^{{\text {ab}}} / (I_K^{{\text {ab}}})^{\times p}$ that is abelian of exponent $p$.

Remark 4.1.5 Similar reasoning applies to abelian varieties over a non-archimedean local field $K$. Raynaud proved that:

• – every abelian variety over $K$ has potentially semistable reduction [GR72, § 3];

• – an abelian variety $E$ of semistable reduction is a rigid analytic quotient of a semiabelian variety $D$ of good reduction by a lattice $\varLambda$ (see [GR72, § 14]).

The Galois action on the lattice $\varLambda$ is always unramified [GR72, § 3, Cor. 3.8]. Consequently, for each prime $\ell$ different from the residual characteristic the $\ell$-adic monodromy representation $\rho _\ell \colon I_K \to \operatorname {GL}(T_\ell E)$ is expressed in terms of the Kummer pairing of $D$ in the same way as in our Lemma 4.1.3. One deduces that $\rho _\ell$ is unipotent of level at most 2, and that $\rho _\ell (P_K) = \{1\}$.

Let us return to the setting of Drinfeld modules. Following § 3.2 we consider Poonen's canonical local height $\|\cdot \|$ on the $A$-module ${D}(K)$. We have seen that with a suitable normalization of the absolute value this height is an $\infty$-adic seminorm. Remarkably, this restricts to a proper norm on every period lattice $\varLambda$.

Lemma 4.1.6 The induced height $\|\cdot \|\colon \varLambda \to \mathbf {Z}_{\geqslant 0}$ has the following properties:

1. (1) $\|\lambda \| = 0$ if and only if $\lambda = 0$;

2. (2) $\|\lambda + \lambda '\| \leqslant \max \{\|\lambda \|, \:\|\lambda '\| \}$;

3. (3) $\|a\lambda \| = |a|_\infty ^s \, \|\lambda \|$ for all $a \in A$;

4. (4) the subset $\{\lambda \in \varLambda,\:\|\lambda \| \leqslant b\}$ is finite for every $b > 0$.

The exponent $s$ in property (3) is the rank of the Drinfeld module ${D}$.

Proof. Properties (2) and (3) hold for the ambient seminorm and property (4) follows since the lattice $\varLambda$ is discrete in ${D}(K)$. We only need to check the first property. Note that $\|\lambda \| = 0$ if and only if $\lambda \in {D}(\mathcal {O}_K)$. The $A$-module $\varLambda ' = \varLambda \cap {D}(\mathcal {O}_K)$ is finite since $\varLambda$ is discrete in ${D}(K)$. Hence, $\varLambda '$ is torsion, and thus zero as the enclosing module $\varLambda$ is torsion-free.

This fits to our definition of a normed lattice (Definition 1.3.2) with a caveat: the homogeneity property (3) holds for a differently normalized $\infty$-adic absolute value. When necessary we will correct for this discrepancy by considering the norm $\|\cdot \|^{{1}/{s}}$.

Theorem 4.1.7 Let $E$ be a Drinfeld module of stable reduction over $\operatorname {Spec} K$ with period lattice $\varLambda$ defined over $K$. Then there is an integer $m\geqslant 0$ such that the monodromy representation $\rho \colon J_K \to \operatorname {GL}({T}_{\text {ad},\bar {\mathfrak {p}}} E)$ maps the ramification subgroup $\smash {J^{m}_K}$ to $1$. Explicitly, if the period lattice $\varLambda$ is generated by elements $\lambda _1, \dotsc, \lambda _n$, then one can take

\[ m = \max \|\lambda_i\| + 1. \]

Proof. By Theorem 3.2.4(1) each homomorphism $[\lambda _i,\ )_{\text {ad}}$ vanishes on the subgroup $\smash {J^{m}_K}$. Since the Kummer pairing is $A$-linear in the first argument it follows that the homomorphism $[\lambda,\ )_{\text {ad}}$ vanishes on $\smash {J^{m}_K}$ for all $\lambda \in \varLambda$. Lemma 4.1.3 implies the result.

In view of Theorem 4.1.7 the following definition makes sense.

Definition 4.1.8 The conductor $\operatorname {\mathfrak {f}}(E/K)$ is the least integer $m\geqslant 0$ such that $\rho (J_K^{m+1}) = 1$.

Lemma 4.1.9 We have $\operatorname {\mathfrak {f}}(E/K) = 0$ if and only if the Drinfeld module $E$ has good reduction.

Proof. We have $J_K^0 = J_K^1$ by Lemma 3.1.2 so $\operatorname {\mathfrak {f}}(E/K) = 0$ if and only if the inertia group $I_K$ acts trivially on $T_\mathfrak {p} E$ for all $\mathfrak {p}\ne \bar {\mathfrak {p}}$. The claim thus follows from Takahashi's good reduction criterion [Tak82].

The invariant $\operatorname {\mathfrak {f}}(E/K)$ relates to conductors of torsion point extensions in the following way. For each proper ideal $\mathfrak {n}$ that is prime to $\bar {\mathfrak {p}}$ consider the extension $K_\mathfrak {n}\subset K^s$ generated by the $\mathfrak {n}$-torsion points of $E$, which is to say, the group $\operatorname {Gal}(K^s/K_\mathfrak {n})$ is the kernel of the torsion points representation $G_K \to \operatorname {GL}(E[\mathfrak {n}])$. Let ${K_\mathfrak {n}}^{\kern -.9ex\circ }\subset K_\mathfrak {n}$ be the maximal unramified subextension.

Lemma 4.1.10 The extensions $K_\mathfrak {n}/{K_\mathfrak {n}}^{\kern -.9ex\circ }$ are abelian and their conductors are related to $\operatorname {\mathfrak {f}}(E/K)$ as follows. If $\operatorname {\mathfrak {f}}(E/K) \ne 0$, then we have an equality

\[ \operatorname{\mathfrak{f}}(E/K) + 1 = \max_\mathfrak{n}\,\operatorname{\mathfrak{f}}(K_\mathfrak{n}/{K_\mathfrak{n}}^{\kern-.9ex\circ}). \]

If $\operatorname {\mathfrak {f}}(E/K) = 0$, then $\operatorname {\mathfrak {f}}(K_\mathfrak {n}/{K_\mathfrak {n}}^{\kern -.9ex\circ }) = 0$ for all $\mathfrak {n}$.

Proof. The Galois representation $E[\mathfrak {n}]$ and $E[\mathfrak {n}\rangle$ are non-canonically isomorphic, cf. § 2.3. Thus, the Galois group of the extension $K_\mathfrak {n}/{K_\mathfrak {n}}^{\kern -.9ex\circ }$ is the image of the absolute inertia subgroup $I_K$ under the torsion points representation $G_K \to \operatorname {GL}(E[\mathfrak {n}\rangle )$. The latter is obtained from the adelic Tate module representation by reduction modulo the ideal $\mathfrak {n}{A}_{\text {ad},\bar {\mathfrak {p}}}$. Hence, the extension $K_\mathfrak {n}/{K_\mathfrak {n}}^{\kern -.9ex\circ }$ is abelian by Corollary 4.1.4. When this extension is nontrivial its conductor and its highest break in upper numbering $b(K_\mathfrak {n}/{K_\mathfrak {n}}^{\kern -.9ex\circ })$ are related in the following way:

\[ \operatorname{\mathfrak{f}}(K_\mathfrak{n}/{K_\mathfrak{n}}^{\kern-.9ex\circ}) = b(K_\mathfrak{n}/{K_\mathfrak{n}}^{\kern-.9ex\circ}) + 1; \]

see [Ser67, § 4.2, Proposition 1]. In view of this formula our claim is immediate.

The normalization of the conductor $\operatorname {\mathfrak {f}}(E/K)$ thus differs by $1$ from the one of local class field theory. In our case this choice leads to better-looking formulas.

Lemma 4.1.11 The conductor $\operatorname {\mathfrak {f}}(E/K)$ is either zero or a positive integer that is prime to $p$.

Proof. If $m \geqslant 0$ is an integer that is divisible by $p$, then we have $J_K^{m} = J_K^{m+1}$ by Lemma 3.1.2.

Lemma 4.1.12 The conductor is an isogeny invariant.

Proof. We have to be careful as we do not fix the characteristic homomorphism of our Drinfeld modules. In addition, in this proof it will be more convenient to represent Drinfeld modules by homomorphisms $A \to K[\tau ]$.

Let $\varphi, \psi \colon A \to K[\tau ]$ be Drinfeld modules and let $f\colon \varphi \to \psi$ be an isogeny, i.e. a nonzero element of $K[\tau ]$ satisfying $f \varphi (a) = \psi (a) f$ for all $a \in A$. Write $f = g\,\tau ^n$ with $g \in K[\tau ]$ having nonzero constant coefficient. We have a well-defined homomorphism

\[ \varphi'\colon A \to K[\tau], \quad a \mapsto \tau^n \varphi(a) \tau^{-n}. \]

One checks easily that $\varphi '$ is a Drinfeld module. The identity $f \, \varphi (a) = \psi (a) f$ implies that $g \varphi '(a) = \psi (a) g$ so $g$ is an isogeny from $\varphi '$ to $\psi$. Likewise $\tau ^n$ is an isogeny from $\varphi$ to $\varphi '$.

As the constant coefficient of $g$ is nonzero it follows that the characteristic homomorphisms of $\varphi '$ and $\psi$ are the same. The characteristic homomorphisms $\chi _\varphi$ and $\chi _{\varphi '}$ are related by the formula

\[ \chi_{\varphi'} = \sigma^n \circ \chi_\varphi, \]

where $\sigma \colon K \to K$ is the $q$th power map. In particular, if $\varphi$ has finite residual characteristic, then so do $\varphi '$ and $\psi$, and the residual characteristics of $\varphi$, $\varphi '$ and $\psi$ coincide. We will denote these residual characteristics by $\bar {\mathfrak {p}}$ as usual.

Next, suppose that $\varphi$ has stable reduction. It then follows by Lemma 6.1.5(1) of [Pap23] that $\varphi '$ also has stable reduction. Suppose further that $\psi$ also has stable reduction. By Theorem 6.2.12 of [Pap23] the isogeny $g$ induces a Galois-equivariant injective morphism of period lattices $g\colon \varLambda _{\varphi '} \hookrightarrow \varLambda _\psi$. Assuming that $\varLambda _\psi \subset K$ we thus conclude that $\varLambda _{\varphi '} \subset K$.

It therefore suffices to prove our lemma in two cases: (1) $f = \tau ^n$ and (2) the constant coefficient of $f$ is nonzero. In the case $f = \tau ^n$ the map $\sigma ^n$ defines a Galois-equivariant isomorphism of torsion modules $\varphi [a] \xrightarrow {\smash {{ {\sim }}}} \psi [a]$ for all $a \in A$. Invoking Lemma 2.4.4 we obtain a Galois-equivariant isomorphism ${T}_{\text {ad},\bar {\mathfrak {p}}}(\varphi ) \xrightarrow {\smash {{ {\sim }}}} {T}_{\text {ad},\bar {\mathfrak {p}}}(\psi )$, and the claim follows.

Finally, we consider the case when the constant coefficient of $f$ is not zero. We observed above that in this case the characteristic homomorphisms of $\varphi$ and $\psi$ coincide. As a consequence there is an isogeny $f'\colon \psi \to \varphi$ which is dual to $f$ in the sense that $f' f = \varphi (a)$ for some nonzero $a \in A$. Since the multiplication by $a$ is injective on ${T}_{\text {ad},\bar {\mathfrak {p}}}(\varphi )$ the isogeny $f$ induces a Galois-equivariant injective morphism ${T}_{\text {ad},\bar {\mathfrak {p}}}(\varphi ) \hookrightarrow {T}_{\text {ad},\bar {\mathfrak {p}}}(\psi )$. By definition of the conductor this implies that $\operatorname {\mathfrak {f}}(\varphi /K) \leqslant \operatorname {\mathfrak {f}}(\psi /K)$.

The identity $f f' f = f \varphi (a) = \psi (a) f$ implies that $f f' = \psi (a)$ because the ring $K[\tau ]$ is a domain. Repeating the argument above we deduce an inequality $\operatorname {\mathfrak {f}}(\psi /K) \leqslant \operatorname {\mathfrak {f}}(\varphi /K)$, and the lemma follows.

The ramification filtration of the group $J_K$ changes in a nontrivial way when one passes to a finite separable extension $L/K$. It is not generally true that $J_L^m$ maps into $J_K^m$, cf. the proof of Theorem 4.2.1 for a precise statement. The conductor thus depends on the choice of the field $K$ which we reflect in the notation $\operatorname {\mathfrak {f}}(E/K)$. Note that we only consider conductors of Drinfeld modules of stable reduction under the extra assumption that the period lattice is defined over $K$.

Calculating the conductor is a hard problem in general. However, we have a full answer for a class of period lattices $\varLambda$.

Theorem 4.1.13 Let $E$ be a Drinfeld module of stable reduction over $\operatorname {Spec} K$ with period lattice $\varLambda$ defined over $K$. Suppose that elements $\lambda _1, \dotsc, \lambda _n$ generate an $A$-submodule of finite index in $\varLambda$. We then have an inequality

\[ \operatorname{\mathfrak{f}}(E/K) \leqslant {\max} \|\lambda_i\|. \]

If, in addition, the maximum $b = {\max } \|\lambda _i\|$ is prime to $p$ then the following hold.

1. (1) The adelic monodromy representation $\rho \colon J_K \to \operatorname {GL}({T}_{\text {ad},\bar {\mathfrak {p}}} E)$ maps the ramification subgroup $J_K^{b}$ to an infinite subgroup. In particular,

   \[ \operatorname{\mathfrak{f}}(E/K) = {\max} \|\lambda_i\|. \]

2. (2) For every prime $\mathfrak {p}$ different from the residual characteristic $\bar {\mathfrak {p}}$ the $\mathfrak {p}$-adic monodromy representation $\rho _{\mathfrak {p}}\colon J_K \to \operatorname {GL}(T_\mathfrak {p} E)$ maps the subgroup $J_K^{b}$ to an infinite subgroup.

Proof. Since the conductor is invariant under isogenies we are free to assume that the period lattice $\varLambda$ is generated by the vectors $\lambda _1, \dotsc, \lambda _n$. The inequality $\operatorname {\mathfrak {f}}(E/K) \leqslant {\max } \|\lambda _i\|$ then follows from Theorem 4.1.7.

Next assume that the maximum $b = {\max } \|\lambda _i\|$ is prime to $p$ and let $\lambda _i$ be a vector on which the maximum is achieved. Theorem 3.2.4(2) shows that the homomorphism $[\lambda _i,\ )_{\text {ad}}$ maps the ramification subgroup $J_K^b$ surjectively onto ${T}_{\text {ad},\bar {\mathfrak {p}}} {D}$. Claim (1) is then a consequence of Lemma 4.1.3 and claim (2) follows since the natural projection ${T}_{\text {ad},\bar {\mathfrak {p}}}{D} \twoheadrightarrow T_\mathfrak {p}{D}$ is surjective.

One important consequence of this theorem is that all the values of the conductor not forbidden by Lemma 4.1.11 do actually occur.

Corollary 4.1.14 For every integer $m \geqslant 1$, $p \nmid m$, there exists a Drinfeld module over $\operatorname {Spec} K$ of rank $2$ and conductor $m$. In particular, the conductor of a Drinfeld module can be arbitrarily large.

By analogy with the classical theory of lattices one defines the $i$th successive minimum $\mu _i(\varLambda )$ as the minimal real number $b \geqslant 0$ such that the set of vectors $\{\lambda \in \varLambda,\:\|\lambda \| \leqslant b\}$ generates an $A$-submodule of rank at least $i$. Theorem 4.1.13 implies that

\[ \operatorname{\mathfrak{f}}(E/K) \leqslant \mu_n(\varLambda), \]

where $\mu _n(\varLambda )$ is the last successive minimum, $n = \operatorname {rank} \varLambda$.

Finally, let us bring the lattice theory of § 1 to bear on the problem of estimating the conductor.

Theorem 4.1.15 Let $E$ be a Drinfeld module of stable reduction over $\operatorname {Spec} K$ with period lattice $\varLambda$ defined over $K$. Let $r$ be the rank of $E$ and set $s: = r - \operatorname {rank}\varLambda$. Then we have an inequality,

\[ \operatorname{\mathfrak{f}}(E/K) \leqslant \operatorname{vol}(\varLambda)^s \, C^{s(r-s)}, \]

where:

• – $\operatorname {vol}(\varLambda )$ is the volume of the normed lattice $(\varLambda,\|\cdot \|^{{1}/{s}})$;

• – $C = {|\kappa |}^{3g + 2f - 1}$;

• – $\kappa$ is the field of constants of the coefficient field $F$;

• – $g$ is the genus of the coefficient field $F$;

• – $f$ is the degree of the place $\infty$ over $\kappa$.

Proof. Every nonzero period $\lambda \in \varLambda$ satisfies the inequality $\|\lambda \|^{{1}/{s}} \geqslant 1$. Hence, Theorem 1.6.4 implies that the $A$-module $\varLambda$ is generated by the subset

\[ \{\lambda \in \varLambda, \:\|\lambda\|^{{1}/{s}} \leqslant \operatorname{vol}(\varLambda) \, C^{r-s} \}. \]

In view of this fact, the bound on the conductor follows from Theorem 4.1.7.

Whenever $\operatorname {vol}(\varLambda ) \cdot C^{r-s} \ne 1$ one can tighten the bound in Theorem 4.1.15 by $1$ by appealing to Lemma 4.1.11.

4.2 General results

Theorem 4.2.1 Let $E$ be a Drinfeld module of finite residual characteristic $\bar {\mathfrak {p}}$ over $\operatorname {Spec} K$ and let $\rho \colon G_K \to \operatorname {GL}({T}_{\text {ad},\bar {\mathfrak {p}}} E)$ be its restricted adelic Tate module representation. Then there is a rational number $u\geqslant 0$ such that $\rho (I_K^u) = 1$.

Proof. Let $L\subset K^s$ be a finite Galois extension of $K$ such that $E$ has stable reduction over $\operatorname {Spec} L$ and the local period lattice of $E$ is defined over $L$. Theorem 4.1.7 shows that $\rho (I_L^u) = 1$ for all rational numbers $u \gg 0$. We have a short exact sequence of groups

where $\varphi$ is the lower-to-upper reindexing function of the extension $L/K$ (see [Ser68, Chapitre IV, § 3]). Taking a sufficiently large rational number $u$ we ensure that $\operatorname {Gal}(L/K)^{\varphi (u)} = 1$, and the claim follows.

Theorem 4.2.2 Let $E$ be a Drinfeld module of finite residual characteristic $\bar {\mathfrak {p}}$ and rank $r$ over $\operatorname {Spec} K$. Suppose that the local period lattice of $E$ has rank $1$. Then the group scheme $\operatorname {GL}({T}_{\text {ad},\bar {\mathfrak {p}}} E)$ contains a closed subgroup scheme $U \cong \smash {(\mathbf {G}_a)^{\times (r-1)}}$ such that the image of inertia is commensurable with $U({A}_{\text {ad},\bar {\mathfrak {p}}})$.

Proof. Since we are free to replace the field $K$ by a finite separable extension we assume that $E$ has stable reduction and that its local period lattice $\varLambda$ is defined over $K$. As in § 4.1 we have a short exact sequence of Galois representations in finitely generated free ${A}_{\text {ad},\bar {\mathfrak {p}}}$-modules:

This defines an ${A}_{\text {ad},\bar {\mathfrak {p}}}$-module flag on the middle term. Let $U$ be the corresponding unipotent subgroup scheme of $\operatorname {GL}({T}_{\text {ad},\bar {\mathfrak {p}}} E)$. By our assumption the period lattice $\varLambda$ is an invertible $A$-module. Hence, the group scheme $U$ is isomorphic to $(\mathbf {G}_a)^{\times d}$ where

\[ d = \operatorname{rank}({T}_{\text{ad},\bar{\mathfrak{p}}}{D}) = r - 1. \]

The image of inertia $\varGamma$ is contained in the subgroup $U({A}_{\text {ad},\bar {\mathfrak {p}}})$ since the representations ${T}_{\text {ad},\bar {\mathfrak {p}}}{D}$ and $\varLambda$ are unramified.

Pick a nonzero period $\lambda \in \varLambda$. As the period lattice $\varLambda$ has rank $1$ the evaluation at $\lambda$ defines an open embedding:

\[ \operatorname{Hom}_A(\varLambda,{T}_{\text{ad},\bar{\mathfrak{p}}}{D}) \hookrightarrow {T}_{\text{ad},\bar{\mathfrak{p}}}{D}. \]

By Theorem 3.3.2 the homomorphism $[\lambda,\ )_{\text {ad}}$ has open image. Lemma 4.1.3 implies that the subgroup $\varGamma$ is open in $U({A}_{\text {ad},\bar {\mathfrak {p}}}) \xrightarrow {\smash {{ {\sim }}}} \operatorname {Hom}_A(\varLambda,\,{T}_{\text {ad},\bar {\mathfrak {p}}}{D})$. Consequently, the index of $\varGamma$ in $U({A}_{\text {ad},\bar {\mathfrak {p}}})$ is finite.