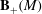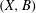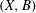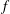Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Fukuda, Shigetaka
2015.
Note on Quasi-Numerically Positive Log Canonical Divisors.
Journal of Mathematics,
Vol. 2015,
Issue. ,
p.
1.
Birkar, Caucher
and
Chen, Jungkai Alfred
2015.
Varieties fibred over abelian varieties with fibres of log general type.
Advances in Mathematics,
Vol. 270,
Issue. ,
p.
206.
Birkar, Caucher
and
Zhang, De-Qi
2016.
Effectivity of Iitaka fibrations and pluricanonical systems of polarized pairs.
Publications mathématiques de l'IHÉS,
Vol. 123,
Issue. 1,
p.
283.
Birkar, Caucher
2017.
The augmented base locus of real divisors over arbitrary fields.
Mathematische Annalen,
Vol. 368,
Issue. 3-4,
p.
905.
Hashizume, Kenta
2018.
Minimal model theory for relatively trivial log canonical pairs.
Annales de l'Institut Fourier,
Vol. 68,
Issue. 5,
p.
2069.
Hashizume, Kenta
2019.
Remarks on special kinds of the relative log minimal model program.
manuscripta mathematica,
Vol. 160,
Issue. 3-4,
p.
285.
Hashizume, Kenta
and
Hu, Zheng-Yu
2020.
On minimal model theory for log abundant lc pairs.
Journal für die reine und angewandte Mathematik (Crelles Journal),
Vol. 2020,
Issue. 767,
p.
109.
Hashizume, Kenta
2024.
Finiteness of log Abundant log Canonical Pairs in log Minimal Model Program with Scaling.
Michigan Mathematical Journal,
Vol. 74,
Issue. 5,
Choi, Sung Rak
Jang, Sungwook
and
Lee, Dae-Won
2025.
On Minimal Model Program and Zariski Decomposition of Potential Triples.
Taiwanese Journal of Mathematics,
Vol. -1,
Issue. -1,