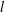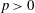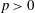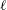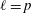Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
ČESNAVIČIUS, KĘSTUTIS
2018.
The ℓ-parity conjecture over the constant quadratic extension.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 165,
Issue. 3,
p.
385.
Lai, King-Fai
Longhi, Ignazio
Suzuki, Takashi
Tan, Ki-Seng
and
Trihan, Fabien
2021.
On the μ-invariants of abelian varieties over function fields of positive characteristic.
Algebra & Number Theory,
Vol. 15,
Issue. 4,
p.
863.
Yuan, Xinyi
2021.
Positivity of Hodge bundles of abelian varieties over some function fields.
Compositio Mathematica,
Vol. 157,
Issue. 9,
p.
1964.