Article contents
A Markov model for Selmer ranks in families of twists
Published online by Cambridge University Press: 30 June 2014
Abstract
We study the distribution of 2-Selmer ranks in the family of quadratic twists of an elliptic curve 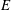 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}E$ over an arbitrary number field
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}E$ over an arbitrary number field 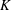 $K$. Under the assumption that
$K$. Under the assumption that 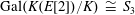 ${\rm Gal}(K(E[2])/K) \ {\cong }\ S_3$, we show that the density (counted in a nonstandard way) of twists with Selmer rank
${\rm Gal}(K(E[2])/K) \ {\cong }\ S_3$, we show that the density (counted in a nonstandard way) of twists with Selmer rank  $r$ exists for all positive integers
$r$ exists for all positive integers  $r$, and is given via an equilibrium distribution, depending only on a single parameter (the ‘disparity’), of a certain Markov process that is itself independent of
$r$, and is given via an equilibrium distribution, depending only on a single parameter (the ‘disparity’), of a certain Markov process that is itself independent of 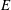 $E$ and
$E$ and 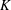 $K$. More generally, our results also apply to
$K$. More generally, our results also apply to 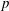 $p$-Selmer ranks of twists of two-dimensional self-dual
$p$-Selmer ranks of twists of two-dimensional self-dual 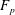 ${\bf F}_p$-representations of the absolute Galois group of
${\bf F}_p$-representations of the absolute Galois group of 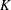 $K$ by characters of order
$K$ by characters of order 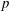 $p$.
$p$.
Information
- Type
- Research Article
- Information
- Copyright
- © The Author(s) 2014
References
- 12
- Cited by

