No CrossRef data available.
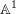 $\mathbb{A}^{1}$-homotopy invariants of topological Fukaya categories of surfaces
$\mathbb{A}^{1}$-homotopy invariants of topological Fukaya categories of surfacesPublished online by Cambridge University Press: 09 June 2017
We provide an explicit formula for localizing 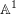 $\mathbb{A}^{1}$-homotopy invariants of topological Fukaya categories of marked surfaces. Following a proposal of Kontsevich, this differential
$\mathbb{A}^{1}$-homotopy invariants of topological Fukaya categories of marked surfaces. Following a proposal of Kontsevich, this differential 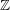 $\mathbb{Z}$-graded category is defined as global sections of a constructible cosheaf of dg categories on any spine of the surface. Our theorem utilizes this sheaf-theoretic description to reduce the calculation of invariants to the local case when the surface is a boundary-marked disk. At the heart of the proof lies a theory of localization for topological Fukaya categories which is a combinatorial analog of Thomason–Trobaugh’s theory of localization in the context of algebraic
$\mathbb{Z}$-graded category is defined as global sections of a constructible cosheaf of dg categories on any spine of the surface. Our theorem utilizes this sheaf-theoretic description to reduce the calculation of invariants to the local case when the surface is a boundary-marked disk. At the heart of the proof lies a theory of localization for topological Fukaya categories which is a combinatorial analog of Thomason–Trobaugh’s theory of localization in the context of algebraic 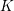 $K$-theory for schemes.
$K$-theory for schemes.