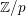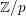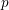Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Koymans, Peter
and
Pagano, Carlo
2024.
Two-step nilpotent extensions are not anabelian.
Mathematische Zeitschrift,
Vol. 306,
Issue. 2,
Koenigsmann, Jochen
and
Strommen, Kristian
2024.
Recovering p$p$‐adic valuations from pro‐p$p$ Galois groups.
Journal of the London Mathematical Society,
Vol. 109,
Issue. 5,