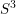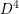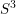Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Conway, James
Etnyre, John B
and
Tosun, Bülent
2021.
Symplectic Fillings, Contact Surgeries, and Lagrangian Disks.
International Mathematics Research Notices,
Vol. 2021,
Issue. 8,
p.
6020.
McCullough, Andrew
2023.
Legendrian large cables and new phenomenon for nonuniformly thick knots.
Algebraic & Geometric Topology,
Vol. 23,
Issue. 6,
p.
2561.