No CrossRef data available.
Article contents
Modular forms of half-integral weight on exceptional groups
Published online by Cambridge University Press: 22 February 2024
Abstract
We define a notion of modular forms of half-integral weight on the quaternionic exceptional groups. We prove that they have a well-behaved notion of Fourier coefficients, which are complex numbers defined up to multiplication by 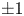 ${\pm }1$. We analyze the minimal modular form
${\pm }1$. We analyze the minimal modular form 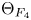 $\Theta _{F_4}$ on the double cover of
$\Theta _{F_4}$ on the double cover of 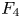 $F_4$, following Loke–Savin and Ginzburg. Using
$F_4$, following Loke–Savin and Ginzburg. Using 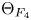 $\Theta _{F_4}$, we define a modular form of weight
$\Theta _{F_4}$, we define a modular form of weight 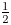 $\tfrac {1}{2}$ on (the double cover of)
$\tfrac {1}{2}$ on (the double cover of) 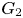 $G_2$. We prove that the Fourier coefficients of this modular form on
$G_2$. We prove that the Fourier coefficients of this modular form on 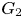 $G_2$ see the
$G_2$ see the 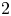 $2$-torsion in the narrow class groups of totally real cubic fields.
$2$-torsion in the narrow class groups of totally real cubic fields.
Keywords
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- © 2024 The Author(s). The publishing rights in this article are licensed to Foundation Compositio Mathematica under an exclusive licence
Footnotes
SL has been supported by an AMS-Simons Travel Award and by NSF grant DMS-1902865. AP has been supported by the Simons Foundation via Collaboration Grant number 585147, by the NSF via grant numbers 2101888 and 2144021, and by an AMS Centennial Research Fellowship.


