Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-10T16:47:29.206Z Has data issue: false hasContentIssue false
  • English
  • Français

Modularity of nearly ordinary 2-adic residually dihedral Galois representations

Part of: Algebraic number theory: global fields Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  16 June 2014

Patrick B. Allen
Patrick B. Allen*
Affiliation:
Department of Mathematics, Northwestern University, 2033 Sheridan Road, Evanston, IL 60208-2730, USA email pballen@math.northwestern.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We prove modularity of some two-dimensional, 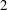$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}2$-adic Galois representations over a totally real field that are nearly ordinary at all places above 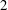$2$ and that are residually dihedral. We do this by employing the strategy of Skinner and Wiles, using Hida families, together with the 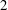$2$-adic patching method of Khare and Wintenberger. As an application we deduce modularity of some elliptic curves over totally real fields that have good ordinary or multiplicative reduction at places above 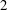$2$.

Keywords

Galois representationsHilbert modular forms

MSC classification

Secondary: 11F80: Galois representations 11R39: Langlands-Weil conjectures, nonabelian class field theory
Type
Research Article
Information
Compositio Mathematica , Volume 150 , Issue 8 , August 2014 , pp. 1235 - 1346
Copyright
© The Author 2014 

References

Artin, E. and Tate, J., Class field theory (W.A. Benjamin, New York, 1968).Google Scholar
Blasius, D. and Rogawski, J., Motives for Hilbert modular forms, Invent. Math. 114 (1993), 55–87.CrossRefGoogle Scholar
Bourbaki, N., Algèbre commutative (Herman, Paris, 1962).Google Scholar
Carayol, H., Sur les représentations l-adique associèes aux formes modulaires de Hilbert, Ann. Sci. É. Norm. Super. (4) 19 (1986), 409–468.Google Scholar
Carayol, H., Formes modulaires et représentations galoisiennes à valeurs dans un anneau local complet, in p-adic monodromy and the Birch and Swinnerton–Dyer conjecture (Boston, MA, 1991), Contemporary Mathematics, vol. 165 (American Mathematical Society, Providence, RI, 1994), 213–237.Google Scholar
Darmon, H., Diamond, F. and Taylor, R., Fermat’s last theorem, in Current developments in mathematics, 1995 (Cambridge, MA) (International Press, Cambridge, MA, 1994), 1–154.Google Scholar
Dickinson, M., On the modularity of certain 2-adic Galois representations, Duke Math. J. 109 (2001), 319–382.Google Scholar
Flenner, H., O’Carroll, L. and Vogel, W., Joins and intersections, Springer Monographs in Mathematics (Springer, Berlin, 1999).Google Scholar
Geraghty, D., Modularity lifting theorems for ordinary Galois representations, Preprint (2010). Available at https://www2.bc.edu/david-geraghty/files/oml.pdf.Google Scholar
Grothendieck, A., Eléments de géométrie algébrique: IV. Étude locale des schémas et des morphismes de schémas I. Publ. Math. Inst. Hautes Études Sci. 20 (1964).Google Scholar
Grothendieck, A., Eléments de géométrie algébrique: IV. Étude locale des schémas et des morphismes de schémas II. Publ. Math. Inst. Hautes Études Sci. 24 (1965).CrossRefGoogle Scholar
Grothendieck, A., Eléments de géométrie algébrique: IV. Étude locale des schémas et des morphismes de schémas III. Publ. Math. Inst. Hautes Études Sci. 28 (1966).CrossRefGoogle Scholar
Grothendieck, A., Cohomologie local des faisceaux cohérents et théorèmes de Lefschetz locaux et globaux (SGA 2), Documents Mathématiques (Paris), vol. 4, (Société Mathématique de France, Paris, 2005). Augmenté d’un exposé de Michèle Raynaud. With a preface and edited by Yves Laszlo. Revised reprint of the 1968 French original.Google Scholar
Hida, H., On nearly ordinary Hecke algebras for GL(2) over totally real fields, in Algebraic number theory, Advanced Studies in Pure Mathematics, vol. 17 (Academic Press, Boston, MA, 1989a), 139–169.Google Scholar
Hida, H., Nearly ordinary Hecke algebras and Galois representations of several variables, in Algebraic analysis, geometry, and number theory (Baltimore, MD 1988) (Johns Hopkins University Press, Baltimore, MD, 1989b), 115–134.Google Scholar
Kisin, M., Overconvergent modular forms and the Fontain–Mazur conjecture, Invent. Math. 153 (2003), 373–454.Google Scholar
Kisin, M., Modularity of 2-dimensional Galois representations, Curr. Dev. Maths 2005 (2007), 191–230.Google Scholar
Kisin, M., Moduli of finite flat group schemes and modularity, Ann. of Math. (2) 170 (2009a), 1085–1180.CrossRefGoogle Scholar
Kisin, M., Modularity of 2-adic Barsotti–Tate representations, Invent. Math. 178 (2009b), 587–634.CrossRefGoogle Scholar
Khare, C. and Wintenberger, J.-P., Serre’s modularity conjecture (II), Invent. Math. 178 (2009), 505–586.Google Scholar
Kunz, E., Introduction to plane algebraic curves, ed. Belshoff, G. (Birkhäuser, Boston, MA, 2005).Google Scholar
Labute, J. P., Classification of Demushkin groups, Canad. J. Math. 19 (1967), 106–132.Google Scholar
Matsumura, H., Commutative ring theory, Cambridge Studies in Advanced Mathematics, vol. 8 (Cambridge University Press, Cambridge, 1989).Google Scholar
Mazur, B., Deforming Galois representations, in Workshop on Galois groups over ℚ and related topics (Berkeley, CA, 1987), Mathematical Sciences Research Institute Publications, vol. 16 (Springer, New York, 1989), 385–437.Google Scholar
Milne, J. S., Arithmetic duality theorems, second edition, (BookSurge, LLC, Charleston, SC, 2006).Google Scholar
Neukirch, J., Schmidt, A. and Wingberg, K., Cohomology of number fields, Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], vol. 323 (Springer, Berlin, 2000).Google Scholar
Nyssen, L., Pseudo-représentations, Math. Ann. 306 (1996), 257–283.Google Scholar
Pink, R., Compact subgroups of linear algebraic groups, J. Algebra 206 (1998), 438–504.CrossRefGoogle Scholar
Rouquier, R., Charactérisation des caractères et pseudo-caractères, J. Algebra 180 (1996), 571–586.Google Scholar
Saito, T., Hilbert modular forms and p-adic Hodge theory, Compositio Math. 145 (2009), 1081–1113.CrossRefGoogle Scholar
Serre, J.-P., Structure de certains pro-p groups (d’après Demus̆kin), Séminaire Bourbaki, vol. 8 (Société Mathématique de France, Paris, 1995), 145–155.Google Scholar
Silverman, J. H., The arithmetic of elliptic curves, Graduate Texts in Mathematics, vol. 106 (Springer, New York, 1986).Google Scholar
Skinner, C., A note on the p-adic Galois representations attached to Hilbert modular forms, Doc. Math. 14 (2009), 241–258.Google Scholar
Skinner, C., Nearly ordinary deformations of residually dihedral representations status, Preprint (2009).Google Scholar
Skinner, C. and Wiles, A., Residually reducible representations and modular forms, Publ. Math. Inst. Hautes Études Sci. 89 (2000), 5–126.Google Scholar
Skinner, C. and Wiles, A., Nearly ordinary deformations of residually irreducible representations, Ann. Fac. Sci. Toulouse Math. (6) 10 (2001), 185–215.Google Scholar
Snowden, A., Singularities of ordinary deformation rings, Preprint (2011), arXiv:1111.3654 [math.NT].Google Scholar
Taylor, R., On Galois representations associated to Hilbert modular forms, Invent. Math. 98 (1989), 265–280.Google Scholar
Taylor, R., On the meromorphic continuation of degree two L-functions, Doc. Math. Extra Vol. (2006), 729–779.Google Scholar
Wiles, A., On ordinary λ-adic representations associated to modular forms, Invent. Math. 94 (1988), 529–573.Google Scholar
Zariski, O. and Samuel, P., Commutative algebra. Vol. II, Graduate Texts in Mathematics (Springer, New York, 1975), Reprint of the 1960 edition.Google Scholar