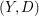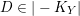Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Allcock, Daniel
2013.
Completions, branched covers, Artin groups, and singularity theory.
Duke Mathematical Journal,
Vol. 162,
Issue. 14,
Mandel, Travis
2016.
Tropical theta functions and log Calabi–Yau surfaces.
Selecta Mathematica,
Vol. 22,
Issue. 3,
p.
1289.
Gross, Mark
Hacking, Paul
Keel, Sean
and
Kontsevich, Maxim
2017.
Canonical bases for cluster algebras.
Journal of the American Mathematical Society,
Vol. 31,
Issue. 2,
p.
497.
Laza, Radu
and
O’Grady, Kieran G.
2018.
Geometry of Moduli.
Vol. 14,
Issue. ,
p.
217.
Coughlan, Stephen
and
Ducat, Tom
2020.
Constructing Fano 3-folds from cluster varieties of rank 2.
Compositio Mathematica,
Vol. 156,
Issue. 9,
p.
1873.
Bergvall, Olof
2020.
On the cohomology of the space of seven points in general linear position.
Research in Number Theory,
Vol. 6,
Issue. 4,
Bousseau, Pierrick
2020.
Quantum mirrors of log Calabi–Yau surfaces and higher-genus curve counting.
Compositio Mathematica,
Vol. 156,
Issue. 2,
p.
360.
Alexeev, Valery
and
Thompson, Alan
2020.
ADE surfaces and their moduli.
Journal of Algebraic Geometry,
Vol. 30,
Issue. 2,
p.
331.
CAVEY, Daniel
and
PRINCE, Thomas
2020.
Del Pezzo surfaces with a single $1/k(1,1)$ singularity.
Journal of the Mathematical Society of Japan,
Vol. 72,
Issue. 2,
Bousseau, Pierrick
2021.
On an Example of Quiver Donaldson–Thomas/Relative Gromov–Witten Correspondence.
International Mathematics Research Notices,
Vol. 2021,
Issue. 15,
p.
11845.
Yu, Tony Yue
2021.
Enumeration of holomorphic cylinders in log
Calabi–Yau surfaces, II : Positivity, integrality and the gluing formula.
Geometry & Topology,
Vol. 25,
Issue. 1,
p.
1.
ODAKA, YUJI
2022.
PL DENSITY INVARIANT FOR TYPE II DEGENERATING K3 SURFACES, MODULI COMPACTIFICATION AND HYPER-KÄHLER METRIC.
Nagoya Mathematical Journal,
Vol. 247,
Issue. ,
p.
574.
Collins, Tristan
Jacob, Adam
and
Lin, Yu-Shen
2022.
The Torelli theorem for gravitational instantons.
Forum of Mathematics, Sigma,
Vol. 10,
Issue. ,
ARGÜZ, HÜLYA
2023.
Equations of mirrors to log Calabi–Yau pairs via the heart of canonical wall structures.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 175,
Issue. 2,
p.
381.
Lee, Tsung-Ju
and
Lin, Yu-Shen
2023.
Period domains for gravitational instantons.
Transactions of the American Mathematical Society,
Vol. 376,
Issue. 8,
p.
5461.
Alexeev, Valery
Engel, Philip
and
Thompson, Alan
2023.
Stable pair compactification of moduli of K3 surfaces of degree 2.
Journal für die reine und angewandte Mathematik (Crelles Journal),
Vol. 0,
Issue. 0,
Monte, Fabrizio Del
and
Longhi, Pietro
2023.
Quiver Symmetries and Wall-Crossing Invariance.
Communications in Mathematical Physics,
Vol. 398,
Issue. 1,
p.
89.
Zhou, Yan
2023.
Weyl Groups and Cluster Structures of Families of Log Calabi–Yau Surfaces.
International Mathematics Research Notices,
Vol. 2023,
Issue. 16,
p.
14290.
Hacking, Paul
and
Keating, Ailsa
2023.
Homological mirror symmetry for log
Calabi–Yau surfaces.
Geometry & Topology,
Vol. 26,
Issue. 8,
p.
3747.
Casalaina-Martin, Sebastian
Grushevsky, Samuel
Hulek, Klaus
and
Laza, Radu
2023.
Cohomology of the Moduli Space of Cubic Threefolds and Its Smooth Models.
Memoirs of the American Mathematical Society,
Vol. 282,
Issue. 1395,