Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-26T08:46:02.792Z Has data issue: false hasContentIssue false
  • English
  • Français

Motohashi’s fourth moment identity for non-archimedean test functions and applications

Part of: Discontinuous groups and automorphic forms Zeta and $L$-functions: analytic theory

Published online by Cambridge University Press:  17 April 2020

Valentin Blomer ,
Peter Humphries ,
Rizwanur Khan  and
Micah B. Milinovich
Valentin Blomer
Affiliation:
Universität Bonn, Mathematisches Institut, Endenicher Allee 60, D-53115Bonn, Germany email blomer@math.uni-bonn.de
Peter Humphries
Affiliation:
Department of Mathematics, University College London, Gower Street, LondonWC1E 6BT, UK email pclhumphries@gmail.com
Rizwanur Khan
Affiliation:
Department of Mathematics, University of Mississippi, University, MS38677, USA email rrkhan@olemiss.edu
Micah B. Milinovich
Affiliation:
Department of Mathematics, University of Mississippi, University, MS38677, USA email mbmilino@olemiss.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Motohashi established an explicit identity between the fourth moment of the Riemann zeta function weighted by some test function and a spectral cubic moment of automorphic 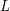$L$-functions. By an entirely different method, we prove a generalization of this formula to a fourth moment of Dirichlet 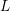$L$-functions modulo 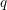$q$ weighted by a non-archimedean test function. This establishes a new reciprocity formula. As an application, we obtain sharp upper bounds for the fourth moment twisted by the square of a Dirichlet polynomial of length 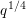$q^{1/4}$. An auxiliary result of independent interest is a sharp upper bound for a certain sixth moment for automorphic 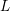$L$-functions, which we also use to improve the best known subconvexity bounds for automorphic 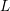$L$-functions in the level aspect.

Keywords

spectral reciprocitymoments of L-functionssubconvexity

MSC classification

Primary: 11M41: Other Dirichlet series and zeta functions 11F72: Spectral theory; Selberg trace formula
Type
Research Article
Information
Compositio Mathematica , Volume 156 , Issue 5 , May 2020 , pp. 1004 - 1038
Copyright
© The Authors 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The first author is supported in part by DFG grant BL 915/2-2. The second author is supported by the European Research Council grant agreement 670239. The third author is supported by the Simons Foundation (award 630985).

References

Bettin, S., Bui, H. M., Li, X. and Radziwiłł, M., A quadratic divisor problem and moments of the Riemann zeta-function, Preprint (2016), arXiv:1609.02539.Google Scholar
Blomer, V., Harcos, G. and Michel, P., Bounds for modular L-functions in the level aspect, Ann. Sci. École Norm. Supér. 40 (2007), 697–740.CrossRefGoogle Scholar
Blomer, V. and Khan, R., Uniform subconvexity and symmetry breaking reciprocity, J. Funct. Anal. 276 (2019), 2315–2358.CrossRefGoogle Scholar
Blomer, V. and Khan, R., Twisted moments of L-functions and spectral reciprocity, Duke Math. J. 168 (2019), 1109–1177.CrossRefGoogle Scholar
Blomer, V. and Milićević, D., The second moment of twisted modular L-functions, Geom. Funct. Anal. 25 (2015), 453–516.CrossRefGoogle Scholar
Conrey, J. B. and Iwaniec, H., The cubic moment of central values of automorphic L-functions, Ann. of Math. (2) 151 (2000), 1175–1216.CrossRefGoogle Scholar
Deshouillers, J.-M. and Iwaniec, H., Kloosterman sums and Fourier coefficients of cusp forms, Invent. Math. 70 (1982), 219–288.CrossRefGoogle Scholar
Duke, W., Friedlander, J. B. and Iwaniec, H., A quadratic divisor problem, Invent. Math. 115 (1994), 209–217.CrossRefGoogle Scholar
Duke, W., Friedlander, J. B. and Iwaniec, H., The subconvexity problem for Artin L-functions, Invent. Math. 149 (2002), 489–577.CrossRefGoogle Scholar
Friedlander, J. and Iwaniec, H., A mean-value theorem for character sums, Michigan Math. J. 39 (1992), 153–159.Google Scholar
Gradshteyn, I. S. and Ryzhik, I. M., Table of integrals, series, and products, seventh edition, eds Jeffrey, A. and Zwillinger, D. (Academic Press, Burlington, MA, 2007).Google Scholar
Harcos, G. and Michel, P., The subconvexity problem for Rankin–Selberg L-functions and equidistribution of Heegner points. II, Invent. Math. 163 (2006), 581–655.CrossRefGoogle Scholar
Harman, G., Watt, N. and Wong, K., A new mean-value result for Dirichlet L-functions and polynomials, Q. J. Math. 55 (2004), 307–324.CrossRefGoogle Scholar
Heath-Brown, D. R., The twelfth power moment of the Riemann-function, Q. J. Math. 29 (1978), 443–462.CrossRefGoogle Scholar
Hough, R., The angle of large values of L-functions, J. Number Theory 167 (2016), 353–393.CrossRefGoogle Scholar
Hughes, C. P. and Young, M. P., The twisted fourth moment of the Riemann zeta function, J. Reine Angew. Math. 641 (2010), 203–236.Google Scholar
Ivić, A., On sums of Hecke series in short intervals, J. Théor. Nombres Bordeaux 13 (2001), 453–468.CrossRefGoogle Scholar
Kıral, E. M. and Young, M. P., The fifth moment of modular L-functions, Preprint (2017), arXiv:1701.07507.Google Scholar
Kıral, E. M. and Young, M. P., Kloosterman sums and Fourier coefficients of Eisenstein series, Ramanujan J. 49 (2019), 391–409.CrossRefGoogle Scholar
Michel, P. and Venkatesh, A., The subconvexity problem for GL2, Publ. Math. Inst. Hautes Études Sci. 111 (2010), 171–271.CrossRefGoogle Scholar
Motohashi, Y., The Riemann zeta-function and the Hecke congruence subgroups, in Analytic number theory, Sūrikaisekikenkyūsho Kōkyōroku, vol. 958 (Research Institute for Mathematical Sciences, Kyoto University, 1996), 166–177.Google Scholar
Motohashi, Y., Spectral theory of the Riemann zeta-function, Cambridge Tracts in Mathematics, vol. 127 (Cambridge University Press, Cambridge, 1997).CrossRefGoogle Scholar
Nelson, P. D., Eisenstein series and the cubic moment for PGL(2), Preprint (2019), arXiv:1911.06310.Google Scholar
Ogg, A., On the eigenvalues of Hecke operators, Math. Ann. 179 (1969), 101–108.Google Scholar
Watt, N., Kloosterman sums and a mean value for Dirichlet polynomials, J. Number Theory 53 (1995), 179–210.CrossRefGoogle Scholar
Watt, N., Bounds for a mean value of character sums, Int. J. Number Theory 4 (2008), 249–293.CrossRefGoogle Scholar
Young, M. P., Explicit calculations with Eisenstein series, J. Number Theory 199 (2019), 1–48.CrossRefGoogle Scholar
Zacharias, R., Mollification of the fourth moment of Dirichlet L-functions, Acta Arith. 191 (2019), 201–257.CrossRefGoogle Scholar
Zacharias, R., Periods and reciprocity I, Int. Math. Res. Not. IMRN (2019), rnz100, https://doi.org/10.1093/imrn/rnz100.CrossRefGoogle Scholar