Hostname: page-component-6bf8c574d5-w79xw Total loading time: 0 Render date: 2025-02-28T10:03:49.913Z Has data issue: false hasContentIssue false
  • English
  • Français

Nearby Lagrangian fibers and Whitney sphere links

Part of: Symplectic geometry, contact geometry Differential topology

Published online by Cambridge University Press:  20 February 2018

Tobias Ekholm  and
Ivan Smith
Tobias Ekholm
Affiliation:
Department of Mathematics, Uppsala University, Box 480, 751 06 Uppsala, Sweden Institut Mittag-Leffler, Aurav. 17, 182 60 Djursholm, Sweden email tobias.ekholm@math.uu.se
Ivan Smith
Affiliation:
Centre for Mathematical Sciences, University of Cambridge, Wilberforce Road, CB3 0WB, UK email is200@cam.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 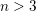$n>3$, and let 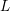$L$ be a Lagrangian embedding of 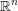$\mathbb{R}^{n}$ into the cotangent bundle 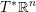$T^{\ast }\mathbb{R}^{n}$ of 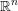$\mathbb{R}^{n}$ that agrees with the cotangent fiber 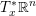$T_{x}^{\ast }\mathbb{R}^{n}$ over a point 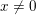$x\neq 0$ outside a compact set. Assume that 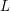$L$ is disjoint from the cotangent fiber at the origin. The projection of 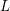$L$ to the base extends to a map of the $n$-sphere 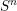$S^{n}$ into 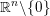$\mathbb{R}^{n}\setminus \{0\}$. We show that this map is homotopically trivial, answering a question of Eliashberg. We give a number of generalizations of this result, including homotopical constraints on embedded Lagrangian disks in the complement of another Lagrangian submanifold, and on two-component links of immersed Lagrangian spheres with one double point in 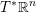$T^{\ast }\mathbb{R}^{n}$, under suitable dimension and Maslov index hypotheses. The proofs combine techniques from Ekholm and Smith [Exact Lagrangian immersions with a single double point, J. Amer. Math. Soc. 29 (2016), 1–59] and Ekholm and Smith [Exact Lagrangian immersions with one double point revisited, Math. Ann. 358 (2014), 195–240] with symplectic field theory.

Keywords

Lagrangian linkWhitney sphereFloer equationmoduli space of holomorphic diskssymplectic field theoryPontrjagin-Thom constructionstable homotopy groups of spheres

MSC classification

Primary: 53D35: Global theory of symplectic and contact manifolds 53D42: Symplectic field theory; contact homology 57R17: Symplectic and contact topology
Type
Research Article
Information
Compositio Mathematica , Volume 154 , Issue 4 , April 2018 , pp. 685 - 718
Copyright
© The Authors 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abouzaid, M., Nearby Lagrangians with vanishing Maslov class are homotopy equivalent , Invent. Math. 189 (2012), 251–313.Google Scholar
Abouzaid, M. and Kragh, T., On the immersion classes of nearby Lagrangians , J. Topol. 9 (2016), 232–244.Google Scholar
Abouzaid, M. and Kragh, T., Simple homotopy equivalence of nearby Lagrangians, Preprint (2016), arXiv:1603.05431.Google Scholar
Abouzaid, M. and Seidel, P., An open string analogue of Viterbo functoriality , Geom. Topol. 14 (2010), 373–440.Google Scholar
Abouzaid, M. and Smith, I., Exact Lagrangians in plumbings , Geom. Funct. Anal. 22 (2012), 785–831.Google Scholar
Audin, M. and Lafontaine, J. (eds), Holomorphic curves in symplectic geometry, Progress in Mathematics, vol. 117 (Birkhäuser, Basel, 1994).Google Scholar
Bourgeois, F., Ekholm, T. and Eliashberg, Y., Effect of Legendrian surgery , Geom. Topol. 16 (2012), 301–389.Google Scholar
Bourgeois, F., Eliashberg, Y., Hofer, H., Wysocki, K. and Zehnder, E., Compactness results in symplectic field theory , Geom. Topol. 7 (2003), 799–888.Google Scholar
Cieliebak, K., Handle attaching in symplectic homology and the chord conjecture , J. Eur. Math. Soc. (JEMS) 4 (2002), 115–142.Google Scholar
Cieliebak, K., Ekholm, T. and Latschev, J., Compactness for holomorphic curves with switching Lagrangian boundary conditions , J. Symplectic Geom. 8 (2010), 267–298.Google Scholar
Cieliebak, K. and Eliashberg, Y., From Stein to Weinstein and back, American Mathematical Society Colloquium Publications, vol. 59 (American Mathematical Society, Providence, RI, 2012).Google Scholar
Cornwell, C., Ng, L. and Sivek, S., Obstructions to Lagrangian concordance , Algebr. Geom. Topol. 16 (2016), 797–824.Google Scholar
Dimitroglou-Rizell, G. and Evans, J., Unlinking and unknottedness of monotone Lagrangian submanifolds , Geom. Topol. 18 (2014), 997–1034.Google Scholar
Ekholm, T., Immersions in the metastable range and spin structures on surfaces , Math. Scand. 83 (1998), 5–41.Google Scholar
Ekholm, T., Non-loose Legendrian spheres with trivial Contact Homology DGA , J. Topol. 9 (2016), 826–848.Google Scholar
Ekholm, T., Eliashberg, Y., Murphy, E. and Smith, I., Constructing exact Lagrangian immersions with few double points , Geom. Funct. Anal. 23 (2013), 1772–1803.Google Scholar
Ekholm, T., Etnyre, J. and Sullivan, M., Non-isotopic Legendrian submanifolds in ℝ2n+1 , J. Differential Geom. 71 (2005), 85–128.Google Scholar
Ekholm, T., Kragh, T. and Smith, I., Lagrangian exotic spheres , J. Topol. Anal. 8 (2016), 375–397.Google Scholar
Ekholm, T. and Lekili, Y., Duality between Lagrangian and Legendrian invariants, Preprint (2017), arXiv:1701.01284.Google Scholar
Ekholm, T., Ng, L. and Shende, V., A complete knot invariant from contact homology , Invent. Math. (2017), doi:10.1007/s00222-017-0761-1.Google Scholar
Ekholm, T. and Smith, I., Exact Lagrangian immersions with one double point revisited , Math. Ann. 358 (2014), 195–240.Google Scholar
Ekholm, T. and Smith, I., Exact Lagrangian immersions with a single double point , J. Amer. Math. Soc. 29 (2016), 1–59.Google Scholar
Eliashberg, Y., Givental, A. and Hofer, H., Introduction to symplectic field theory , Geom. Funct. Anal. Special Volume, II (2000), 560–673.Google Scholar
Eliashberg, Y. and Murphy, E., Lagrangian caps , Geom. Funct. Anal. 23 (2013), 1483–1514.Google Scholar
Fenn, R. and Rolfsen, D., Spheres may link homotopically in 4-sphere , J. Lond. Math. Soc. (2) 34 (1986), 177–184.Google Scholar
Fukaya, K., Seidel, P. and Smith, I., Exact Lagrangian submanifolds in simply-connected cotangent bundles , Invent. Math. 172 (2008), 1–27.CrossRefGoogle Scholar
Gromov, M., Partial Differential Relations (Springer, Berlin, 1986).Google Scholar
Haefliger, A., Plongements différentiables de variétés dans variétés , Comment. Math. Helv. 36 (1961), 47–82.Google Scholar
Kirk, P., Link homotopy with one codimension two component , Trans. Amer. Math. Soc. 319 (1990), 663–688.Google Scholar
Kragh, T., Parametrized ring-spectra and the nearby Lagrangian conjecture , Geom. Topol. 17 (2013), 639–731.Google Scholar
Massey, W. and Rolfsen, D., Homotopy classification of higher-dimensional links , Indiana Univ. Math. J. 34 (1985), 375–391.Google Scholar
Viterbo, C., A new obstruction to embedding Lagrangian tori , Invent. Math. 100 (1990), 301–320.Google Scholar
Welschinger, J.-Y., Effective classes and Lagrangian tori in symplectic four-manifolds , J. Symplectic Geom. 5 (2007), 9–18.Google Scholar