Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-26T07:50:46.385Z Has data issue: false hasContentIssue false
  • English
  • Français

Nonabelian Hodge theory for klt spaces and descent theorems for vector bundles

Part of: Global differential geometry Birational geometry

Published online by Cambridge University Press:  07 February 2019

Daniel Greb ,
Stefan Kebekus ,
Thomas Peternell  and
Behrouz Taji
Daniel Greb
Affiliation:
Essener Seminar für Algebraische Geometrie und Arithmetik, Fakultät für Mathematik, Universität Duisburg–Essen, 45117 Essen, Germany email daniel.greb@uni-due.dehttp://www.esaga.uni-due.de/daniel.greb
Stefan Kebekus
Affiliation:
Mathematisches Institut, Albert-Ludwigs-Universität Freiburg, Ernst-Zermelo-Strasse 1, 79104 Freiburg im Breisgau, Germany Freiburg Institute for Advanced Studies (FRIAS), Freiburg im Breisgau, Germany email stefan.kebekus@math.uni-freiburg.dehttps://cplx.vm.uni-freiburg.de
Thomas Peternell
Affiliation:
Mathematisches Institut, Universität Bayreuth, 95440 Bayreuth, Germany email thomas.peternell@uni-bayreuth.dehttp://www.komplexe-analysis.uni-bayreuth.de
Behrouz Taji
Affiliation:
University of Notre Dame, Department of Mathematics, 278 Hurley, Notre Dame, IN 46556, USA email btaji@nd.eduhttp://sites.nd.edu/b-taji
Get access Rights & Permissions [Opens in a new window]

Abstract

We generalise Simpson’s nonabelian Hodge correspondence to the context of projective varieties with Kawamata log terminal (klt) singularities. The proof relies on a descent theorem for numerically flat vector bundles along birational morphisms. In its simplest form, this theorem asserts that given any klt variety 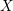$X$ and any resolution of singularities, any vector bundle on the resolution that appears to come from 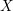$X$ numerically, does indeed come from 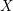$X$. Furthermore, and of independent interest, a new restriction theorem for semistable Higgs sheaves defined on the smooth locus of a normal, projective variety is established.

Keywords

nonabelian Hodge theoryklt singularities

MSC classification

Primary: 14E30: Minimal model program (Mori theory, extremal rays) 53C07: Special connections and metrics on vector bundles (Hermite-Einstein-Yang-Mills)
Type
Research Article
Information
Compositio Mathematica , Volume 155 , Issue 2 , February 2019 , pp. 289 - 323
Copyright
© The Authors 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

DG was partially supported by the DFG-Collaborative Research Center SFB/TR 45. SK gratefully acknowledges support through a joint fellowship of the Freiburg Institute of Advanced Studies (FRIAS) and the University of Strasbourg Institute for Advanced Study (USIAS). BT was partially supported by the DFG-Research Training Group GK1821. Research was partially completed while SK and TP were visiting the National University of Singapore in 2017. TP was supported by the DFG project ‘Zur Positivität in der komplexen Geometrie’.

References

Araujo, C. and Druel, S., On codimension 1 del Pezzo foliations on varieties with mild singularities , Math. Ann. 360 (2014), 769–798.Google Scholar
Barlet, D. and Magnússon, J., Cycles analytiques complexes. I. Théorèmes de préparation des cycles, Cours Spécialisés [Specialized Courses], vol. 22 (Société Mathématique de France, Paris, 2014).Google Scholar
Beltrametti, M. C. and Sommese, A. J., The adjunction theory of complex projective varieties, De Gruyter Expositions in Mathematics, vol. 16 (Walter de Gruyter, Berlin, 1995), doi:10.1515/9783110871746.Google Scholar
Bierstone, E. and Milman, P. D., Canonical desingularization in characteristic zero by blowing up the maximum strata of a local invariant , Invent. Math. 128 (1997), 207–302, doi:10.1007/s002220050141.Google Scholar
Birkar, C., Cascini, P., Hacon, C. D. and McKernan, J., Existence of minimal models for varieties of log general type , J. Amer. Math. Soc. 23 (2010), 405–468, doi:10.1090/S0894-0347-09-00649-3.Google Scholar
Bruzzo, U. and Ruipérez, D. H., Semistability vs. nefness for (Higgs) vector bundles , Differential Geom. Appl. 24 (2006), 403–416, doi:10.1016/j.difgeo.2005.12.007.Google Scholar
Claudon, B., Kebekus, S. and Taji, B., Generic positivity and applications to hyperbolicity of moduli spaces, Preprint (2016), arXiv:1610.09832. To appear as a chapter in a forthcoming book on hyperbolicity, October 2016.Google Scholar
Deligne, P., Équations différentielles à points singuliers réguliers, Lecture Notes in Mathematics, vol. 163 (Springer, Berlin, 1970), doi:10.1007/BFb0061194.Google Scholar
Deligne, P. and Sullivan, D., Fibrés vectoriels complexes à groupe structural discret , C. R. Math. Acad. Sci. Paris Sér. A-B 281 (1975), Ai, A1081–A1083.Google Scholar
Demailly, J.-P., Peternell, T. and Schneider, M., Compact complex manifolds with numerically effective tangent bundles , J. Algebraic Geom. 3 (1994), 295–345.Google Scholar
Grothendieck, A., Éléments de géométrie algébrique. IV. Étude locale des schémas et des morphismes de schémas. Troisiéme partie , Publ. Math. Inst. Hautes Études Sci. 28 (1966), 5–255. Revised in collaboration with Jean Dieudonné, numdam.PMIHES-1966-28-5-0.Google Scholar
Fulton, W., Intersection theory, Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge. A Series of Modern Surveys in Mathematics [Results in Mathematics and Related Areas. 3rd Series. A Series of Modern Surveys in Mathematics], vol. 2, second edition (Springer, Berlin, 1998), doi:10.1007/978-1-4612-1700-8.Google Scholar
Fulton, W. and Lazarsfeld, R., Connectivity and its applications in algebraic geometry , in Algebraic geometry (Chicago, IL, 1980), Lecture Notes in Mathematics, vol. 862 (Springer, Berlin, 1981), 26–92, doi:10.1007/BFb0090889.Google Scholar
Goresky, M. and MacPherson, R. D., Stratified Morse theory, Ergebnisse der Mathematik und ihrer Grenzgebiete (3) [Results in Mathematics and Related Areas (3)], vol. 14 (Springer, Berlin, 1988), doi:10.1007/978-3-642-71714-7.Google Scholar
Görtz, U. and Wedhorn, T., Algebraic geometry I, schemes, with examples and exercises, Advanced Lectures in Mathematics (Vieweg + Teubner, Wiesbaden, 2010), doi:10.1007/978-3-8348-9722-0.Google Scholar
Graf, P. and Kovács, S. J., An optimal extension theorem for 1-forms and the Lipman–Zariski conjecture , Doc. Math. 19 (2014), 815–830.Google Scholar
Greb, D., Kebekus, S., Kovács, S. J. and Peternell, T., Differential forms on log canonical spaces , Publ. Math. Inst. Hautes Études Sci. 114 (2011), 87–169, doi:10.1007/s10240-011-0036-0. An extended version with additional graphics is available as arXiv:1003.2913.Google Scholar
Greb, D., Kebekus, S. and Peternell, T., Étale fundamental groups of Kawamata log terminal spaces, flat sheaves, and quotients of abelian varieties , Duke Math. J. 165 (2016), 1965–2004, doi:10.1215/00127094-3450859.Google Scholar
Greb, D., Kebekus, S., Peternell, T. and Taji, B., The Miyaoka–Yau inequality and uniformisation of canonical models, Ann. Sci. Éc. Norm. Supér. (4), to appear. Preprint (2015),arXiv:1511.08822.Google Scholar
Greb, D., Kebekus, S., Peternell, T. and Taji, B., Harmonic metrics on Higgs sheaves and uniformization of varieties of general type, Preprint (2018), arXiv:1804.01266.Google Scholar
Greb, D., Kebekus, S. and Taji, B., Uniformisation of higher-dimensional varieties , in Algebraic geometry: Salt Lake City 2015, Proceedings of Symposia in Pure Mathematics, vol. 1, eds de Fernex, T., Hassett, B., Mustaţă, M., Olsson, M., Popa, M. and Thomas, R. (American Mathematical Society, Providence, RI, 2018), 277–308.Google Scholar
Grothendieck, A., Représentations linéaires et compactification profinie des groupes discrets , Manuscripta Math. 2 (1970), 375–396, doi:10.1007/BF01719593.Google Scholar
Guenancia, H. and Taji, B., Orbifold stability and Miyaoka–Yau inequality for minimal pairs, Preprint (2016), arXiv:1611.05981.Google Scholar
Hacon, C. D. and McKernan, J., On Shokurov’s rational connectedness conjecture , Duke Math. J. 138 (2007), 119–136; euclid.dmj/1178738561.Google Scholar
Hartshorne, R., Algebraic geometry, Graduate Texts in Mathematics, vol. 52 (Springer, New York, 1977), doi:10.1007/978-1-4757-3849-0.Google Scholar
Hartshorne, R., Stable reflexive sheaves , Math. Ann. 254 (1980), 121–176, doi:10.1007/BF01467074.Google Scholar
Höring, A. and Novelli, C., Mori contractions of maximal length , Publ. Res. Inst. Math. Sci. 49 (2013), 215–228, doi:10.4171/PRIMS/103.Google Scholar
Huybrechts, D. and Lehn, M., The geometry of moduli spaces of sheaves, Cambridge Mathematical Library, second edition (Cambridge University Press, Cambridge, 2010), doi:10.1017/CBO9780511711985.Google Scholar
Kawamata, Y., Matsuda, K. and Matsuki, K., Introduction to the minimal model problem , in Algebraic geometry, Sendai, 1985, Advanced Studies in Pure Mathematics, vol. 10 (North-Holland, Amsterdam, 1987), 283–360.Google Scholar
Kebekus, S., Pull-back morphisms for reflexive differential forms , Adv. Math. 245 (2013), 78–112, doi:10.1016/j.aim.2013.06.013.Google Scholar
Kollár, J., Rational curves on algebraic varieties, Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge. A Series of Modern Surveys in Mathematics [Results in Mathematics and Related Areas. 3rd Series. A Series of Modern Surveys in Mathematics], vol. 32 (Springer, Berlin, 1996), doi:10.1007/978-3-662-03276-3.Google Scholar
Kollár, J., Simultaneous normalization and algebra husks , Asian J. Math. 15 (2011), 437–449, doi:10.4310/AJM.2011.v15.n3.a6.Google Scholar
Kollár, J. and Mori, S., Birational geometry of algebraic varieties, Cambridge Tracts in Mathematics, vol. 134 (Cambridge University Press, Cambridge, 1998); with the collaboration of C. H. Clemens and A. Corti, translated from the 1998 Japanese original, doi:10.1017/CBO9780511662560.Google Scholar
Langer, A., A note on Bogomolov’s instability and Higgs sheaves , in Algebraic geometry (de Gruyter, Berlin, 2002), 237–256.Google Scholar
Langer, A., Bogomolov’s inequality for Higgs sheaves in positive characteristic , Invent. Math. 199 (2015), 889–920, doi:10.1007/s00222-014-0534-z.Google Scholar
Lazarsfeld, R., Positivity in algebraic geometry. I. Classical setting: line bundles and linear series, Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge., vol. 48 (Springer, Berlin, 2004), doi:10.1007/978-3-642-18808-4.Google Scholar
Mochizuki, T., Kobayashi–Hitchin correspondence for tame harmonic bundles and an application , Astérisque 309 (2006).Google Scholar
Mochizuki, T., Asymptotic behaviour of tame harmonic bundles and an application to pure twistor D-modules. I , Mem. Amer. Math. Soc. 185 (2007), doi:10.1090/memo/0869.Google Scholar
Mochizuki, T., Asymptotic behaviour of tame harmonic bundles and an application to pure twistor D-modules. II , Mem. Amer. Math. Soc. 185 (2007), doi:10.1090/memo/0870.Google Scholar
Ribes, L. and Zalesskii, P., Profinite groups, Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge. A Series of Modern Surveys in Mathematics [Results in Mathematics and Related Areas. 3rd Series. A Series of Modern Surveys in Mathematics], vol. 40, second edition (Springer, Berlin, 2010), doi:10.1007/978-3-642-01642-4.Google Scholar
Sabbah, C., Théorie de Hodge et correspondance de Hitchin–Kobayashi sauvages (d’après T. Mochizuki) , Astérisque (2013), (352):Exp. No. 1050, viii, 205–241. Séminaire Bourbaki. Vol. 2011/2012. Exposés 1043–1058.Google Scholar
Grothendieck, A., Cohomologie locale des faisceaux cohérents et théorèmes de Lefschetz locaux et globaux (SGA 2) (North-Holland Publishing Co., Amsterdam, 1968), Augmenté d’un exposé par Michèle Raynaud, Séminaire de Géométrie Algébrique du Bois-Marie, 1962, Advanced Studies in Pure Mathematics, vol. 2. Also available as arXiv:math/0511279.Google Scholar
Simpson, C. T., Harmonic bundles on noncompact curves , J. Amer. Math. Soc. 3 (1990), 713–770, doi:10.2307/1990935.Google Scholar
Simpson, C. T., Higgs bundles and local systems , Publ. Math. Inst. Hautes Études Sci. 75 (1992), 5–95, doi:10.1007/BF02699491, numdam.PMIHES-1992-75-5-0.Google Scholar
Takayama, S., Local simple connectedness of resolutions of log-terminal singularities , Internat. J. Math. 14 (2003), 825–836, doi:10.1142/S0129167X0300196X.Google Scholar