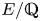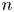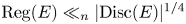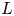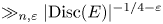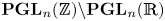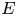Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Nordentoft, Asbjørn Christian
2024.
Wide moments of L-functions I : Twists by class
group characters of imaginary quadratic fields.
Algebra & Number Theory,
Vol. 18,
Issue. 4,
p.
735.