Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-26T08:54:21.910Z Has data issue: false hasContentIssue false
  • English
  • Français

A note on the number of irrational odd zeta values

Part of: Diophantine approximation, transcendental number theory Zeta and $L$-functions: analytic theory

Published online by Cambridge University Press:  09 October 2020

Li Lai  and
Pin Yu
Li Lai
Affiliation:
Department of Mathematics and Yau Mathematical Sciences Center, Tsinghua University, 100084 Beijing, China lilaimath@gmail.com
Pin Yu
Affiliation:
Department of Mathematics and Yau Mathematical Sciences Center, Tsinghua University, 100084 Beijing, China yupin@mail.tsinghua.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove that, for any small 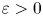$\varepsilon > 0$, the number of irrationals among the following odd zeta values: 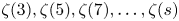$\zeta (3),\zeta (5),\zeta (7),\ldots ,\zeta (s)$ is at least 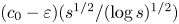$( c_0 - \varepsilon )({s^{1/2}}/{(\log s)^{1/2}})$, provided 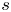$s$ is a sufficiently large odd integer with respect to 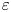$\varepsilon$. The constant 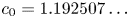$c_0 = 1.192507\ldots$ can be expressed in closed form. Our work improves the lower bound 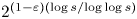$2^{(1-\varepsilon )({\log s}/{\log \log s})}$ of the previous work of Fischler, Sprang and Zudilin. We follow the same strategy of Fischler, Sprang and Zudilin. The main new ingredient is an asymptotically optimal design for the zeros of the auxiliary rational functions, which relates to the inverse totient problem.

Keywords

irrationalityzeta valueshypergeometric series

MSC classification

Primary: 11J72: Irrationality; linear independence over a field
Secondary: 11M06: $zeta (s)$ and $L(s, chi)$ 33C20: Generalized hypergeometric series, $_pF_q$
Type
Research Article
Information
Compositio Mathematica , Volume 156 , Issue 8 , August 2020 , pp. 1699 - 1717
Copyright
Copyright © The Author(s) 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Apéry, R., Irrationalité de $\zeta (2)$ et $\zeta (3)$, in Journées Arithmétiques (Luminy, 1978), Astérisque, vol. 61 (Société Mathématique de France, Paris, 1979), 11–13.Google Scholar
Ball, K. and Rivoal, T., Irrationalité d'une infinité de valeurs de la fonction zêta aux entiers impairs, Invent. Math. 146 (2001), 193–207.Google Scholar
Bateman, P. T., The distribution of values of the Euler function, Acta Arith. 21 (1972), 329–345.CrossRefGoogle Scholar
Beukers, F., A note on the irrationality of $\zeta (2)$ and $\zeta (3)$, Bull. Lond. Math. Soc. 11 (1979), 268–272.CrossRefGoogle Scholar
Dressler, R. E., A density which counts multiplicity, Pacific J. Math. 34 (1970), 371–378.Google Scholar
Fischler, S., Irrationalité de valeurs de zêta (d'après Apéry, Rivoal, ...), in Séminaire Bourbaki 2002/03, Astérisque, vol. 294 (Société Mathématique de France, Paris, 2004), exp. no. 910, 27–62.Google Scholar
Fischler, S., Irrationality of values of L-functions of Dirichlet characters, J. Lond. Math. Soc. (2) 101 (2020), 857–876.Google Scholar
Fischler, S., Sprang, J. and Zudilin, W., Many values of the Riemann zeta function at odd integers are irrational, C. R. Math. Acad. Sci. Paris 356 (2018), 707–711.CrossRefGoogle Scholar
Fischler, S., Sprang, J. and Zudilin, W., Many odd zeta values are irrational, Compos. Math. 155 (2019), 938–952.Google Scholar
Gantmacher, F. and Krein, M., Oscillation matrices and kernels and small vibrations of mechanical systems, Graduate Texts in Mathematics (AMS Chelsea, Providence, RI, 2002).CrossRefGoogle Scholar
Krattenthaler, C. and Rivoal, T., Hypergéométrie et fonction zêta de Riemann, Mem. Amer. Math. Soc. 186 (2007), no. 875.Google Scholar
Montgomery, H. L. and Vaughan, R. C., Multiplicative number theory I, Cambridge Studies in Advanced Mathematics, vol. 97 (Cambridge University Press, 2006).Google Scholar
Nesterenko, Y., On the linear independence of numbers, Vestnik Moskov. Univ. Ser. I Mat. Mekh. [Moscow Univ. Math. Bull.] 40 (1985), 46–49 [69–74].Google Scholar
Rivoal, T., La fonction zêta de Riemann prend une infinité de valeurs irrationnelles aux entiers impairs, C. R. Acad. Sci. Paris Sér. I Math. 331 (2000), 267–270.CrossRefGoogle Scholar
Rivoal, T. and Zudilin, W., A note on odd zeta values, Sém. Lothar. Combin. 81 (2020), B81b.Google Scholar
Sprang, J., Infinitely many odd zeta values are irrational. By elementary means, Preprint (2018), arXiv:1802.09410 [math.NT].Google Scholar
van der Poorten, A., A proof that Euler missed ... Apéry's proof of the irrationality of $\zeta (3)$. An informal report, Math. Intelligencer 1 (1978–1979), 195–203.CrossRefGoogle Scholar
Zudilin, W., One of the numbers $\zeta (5)$, $\zeta (7)$, $\zeta (9)$, $\zeta (11)$ is irrational, Uspekhi Mat. Nauk 56 (2001), 149–150 (Engl. Transl. Russian Math. Surveys 56 (2001), 774–776).Google Scholar
Zudilin, W., Irrationality of values of the Riemann zeta function, Izv. Ross. Akad. Nauk Ser. Mat. 66 (2002), 49–102 (Engl. Transl. Izv. Math. 66 (2002), 489–542).Google Scholar
Zudilin, W., One of the odd zeta values from $\zeta (5)$ to $\zeta (25)$ is irrational. By elementary means, SIGMA Symmetry Integrability Geom. Methods Appl. 14 (2018), no. 028.Google Scholar