Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-10T20:21:12.721Z Has data issue: false hasContentIssue false
  • English
  • Français

On a filtration of 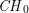$\mathit{CH}_{0}$ for an abelian variety

Part of: Cycles and subschemes

Published online by Cambridge University Press:  22 December 2014

Evangelia Gazaki
Evangelia Gazaki*
Affiliation:
Department of Mathematics, University of Chicago, 5734 University Avenue, Chicago, IL 60637, USA email valiagaz@math.uchicago.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 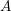$A$ be an abelian variety defined over a field 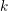$k$. In this paper we define a descending filtration 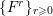$\{F^{r}\}_{r\geqslant 0}$ of the group 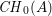$\mathit{CH}_{0}(A)$ and prove that the successive quotients 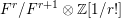$F^{r}/F^{r+1}\otimes \mathbb{Z}[1/r!]$ are isomorphic to the group 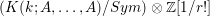$(K(k;A,\dots ,A)/Sym)\otimes \mathbb{Z}[1/r!]$, where 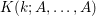$K(k;A,\dots ,A)$ is the Somekawa 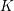$K$-group attached to $r$-copies of the abelian variety 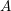$A$. In the special case when 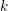$k$ is a finite extension of 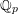$\mathbb{Q}_{p}$ and 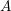$A$ has split multiplicative reduction, we compute the kernel of the map 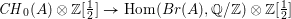$\mathit{CH}_{0}(A)\otimes \mathbb{Z}[\frac{1}{2}]\rightarrow \text{Hom}(Br(A),\mathbb{Q}/\mathbb{Z})\otimes \mathbb{Z}[\frac{1}{2}]$, induced by the pairing 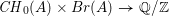$\mathit{CH}_{0}(A)\times Br(A)\rightarrow \mathbb{Q}/\mathbb{Z}$.

Keywords

zero cyclesabelian varietiesSomekawa K-groupBrauer group

MSC classification

Primary: 14C25: Algebraic cycles
Type
Research Article
Information
Compositio Mathematica , Volume 151 , Issue 3 , March 2015 , pp. 435 - 460
Copyright
© The Author 2014 

References

Beauville, A., Quelques remarques sur le transformation de Fourier dans l’anneau de Chow d’une variété abélienne, in Algebraic geometry (Tokyo/Kyoto 1982), Lecture Notes in Mathematics, vol. 1016 (Springer, Berlin, 1983), 238–260.Google Scholar
Beauville, A., Sur l’anneau de Chow d’une variété abélienne, Math. Ann. 273 (1986), 647–651.Google Scholar
Bloch, S., Some elementary theorems about algebraic cycles on Abelian varieties, Invent. Math. 37 (1976), 215–228.Google Scholar
Bloch, S., Lectures on algebraic cycles, second edition (Cambridge University Press, Cambridge, 2010).Google Scholar
Bosh, S., Lütkebohmert, W. and Raynaud, M., Néron models, Ergebnisse der Mathematik und ihrer Grenzgebiete (3), vol. 21 (Springer, Berlin, 1990).Google Scholar
Brown, K., Cohomology of groups, Graduate Text in Mathematics, vol. 87 (Springer, Berlin, 1994).Google Scholar
Colliot-Thélène, J.-L., L’arithmétique du groupe de Chow des zéro-cycles, J. Théor. Nombres Bordeaux 7 (1995), 51–73.Google Scholar
Deninger, C. and Murre, J., Motivic decomposition of abelian schemes and the Fourier transform, J. Reine Angew. Math. 422 (1991), 201–219.Google Scholar
Faltings, G. and Chai, C., Degeneration of abelian varieties, Ergebnisse der Mathematik und ihrer Grenzgebiete, vol. 3 (Springer, Berlin, 1991).Google Scholar
Fulton, W., Intersection theory, Ergebnisse der Mathematik und ihrer Grenzgebiete (3), vol. 2 (Springer, Berlin, 1983).Google Scholar
Grothendieck, A., Le groupe de Brauer I, II, III dans dix exposés sur la cohomollgie des schémas (North-Holland, Amsterdam, 1968), 46–188.Google Scholar
Lichtenbaum, S., Duality theorems for curves over p-adic fields, Invent. Math. 7 (1969), 120–136.Google Scholar
Milne, J. S., Arithmetic duality theorems, second edition (BookSurge, LLC, 2006).Google Scholar
Mukai, S., Duality between D (X) and D (X̂) with its application to Picard Sheaves, Nagoya Math. J. 81 (1981), 153–175.Google Scholar
Murre, J. and Ramakrishnan, D., Local Galois Symbols on E × E, Fields Inst. Commun. 56 (2009).Google Scholar
Raskind, W. and Spiess, M., Milnor K-groups and zero cycles on products of curves over p-adic fields, Compositio Math. 121 (2000), 1–33.Google Scholar
Saito, S., A global duality theorem for varieties over global fileds. Algebraic K-theory, in Connections with geometry and topology (Lake Louise, AB, 1987), NATO Advanced Science Institute Series C: Mathematical and Physical Sciences, vol. 279 (Kluwer Academic Publisher, 1987), 425–444.Google Scholar
Somekawa, M., On Milnor K-groups attached to semi-abelian varieties, K-theory 4 (1990), 105–119.CrossRefGoogle Scholar
Spiess, M. and Yamazaki, T., A counterexample to generalizations of the Milnor–Bloch–Kato conjecture, K-theory 4 (2009), 77–90.Google Scholar
Yamazaki, T., On Chow and Brauer groups of a product of Mumford curves, Math. Ann. 333 (2005), 549–567.Google Scholar