Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-10T23:05:33.973Z Has data issue: false hasContentIssue false
  • English
  • Français

On a lifting problem of L-packets

Part of: Lie groups Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  14 July 2016

Bin Xu
Bin Xu*
Affiliation:
Department of Mathematics and Statistics, University of Calgary, 2500 University Drive NW, Calgary, Alberta, Canada, T2N 1N4 email bin.xu2@ucalgary.ca
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 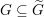$G\subseteq \widetilde{G}$ be two quasisplit connected reductive groups over a local field of characteristic zero and having the same derived group. Although the existence of L-packets is still conjectural in general, it is believed that the L-packets of 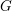$G$ should be the restriction of those of 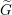$\widetilde{G}$ . Motivated by this, we hope to construct the L-packets of 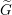$\widetilde{G}$ from those of 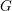$G$ . The primary example in our mind is when 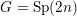$G=\text{Sp}(2n)$ , whose L-packets have been determined by Arthur [The endoscopic classification of representations: orthogonal and symplectic groups, Colloquium Publications, vol. 61 (American Mathematical Society, Providence, RI, 2013)], and 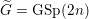$\widetilde{G}=\text{GSp}(2n)$ . As a first step, we need to consider some well-known conjectural properties of L-packets. In this paper, we show how they can be deduced from the conjectural endoscopy theory. As an application, we obtain some structural information about L-packets of 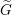$\widetilde{G}$ from those of  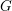$G$ .

Keywords

quasisplit reductive groupsendoscopic transferL-packets

MSC classification

Primary: 22E50: Representations of Lie and linear algebraic groups over local fields
Secondary: 11F70: Representation-theoretic methods; automorphic representations over local and global fields
Type
Research Article
Information
Compositio Mathematica , Volume 152 , Issue 9 , September 2016 , pp. 1800 - 1850
Copyright
© The Author 2016 

References

Adler, J. D. and Prasad, D., On certain multiplicity one theorems , Israel J. Math. 153 (2006), 221–245.Google Scholar
Arthur, J., The endoscopic classification of representations: orthogonal and symplectic groups, Colloquium Publications, vol. 61 (American Mathematical Society, Providence, RI, 2013).Google Scholar
Borel, A., Automorphic L-functions , in Automorphic forms, representations and L-functions (Proc. Sympos. Pure Math., Oregon State Univ., Corvallis, OR, 1977), Part 2, Proceedings of Symposia in Pure Mathematics, vol. XXXIII (American Mathematical Society, Providence, RI, 1979), 27–61.Google Scholar
Bouaziz, A., Sur les caractères des groupes de Lie réductifs non connexes , J. Funct. Anal. 70 (1987), 1–79; MR 870753 (89c:22020).Google Scholar
Clozel, L., Characters of non-connected, reductive p-adic groups , Can. J. Math. 39 (1987), 149–167.Google Scholar
Deligne, P., Les constantes locales de l’équation fonctionnelle de la fonction L d’Artin d’une représentation orthogonale , Invent. Math. 35 (1976), 299–316.CrossRefGoogle Scholar
Gan, W. T., Gross, B. H. and Prasad, D., Symplectic local root numbers, central critical L values, and restriction problems in the representation theory of classical groups , Astérisque 346 (2012), 1–109; Sur les conjectures de Gross et Prasad. I.Google Scholar
Gelbart, S. S. and Knapp, A. W., L-indistinguishability and R groups for the special linear group , Adv. Math. 43 (1982), 101–121.Google Scholar
Harish-Chandra, Invariant eigendistributions on semisimple Lie groups , Bull. Amer. Math. Soc. 69 (1963), 117–123.Google Scholar
Harish-Chandra, Harmonic analysis on real reductive groups. I. The theory of the constant term , J. Funct. Anal. 19 (1975), 104–204.Google Scholar
Harish-Chandra, Admissible invariant distributions on reductive p-adic groups, University Lecture Series, vol. 16(American Mathematical Society, Providence, RI, 1999), preface and notes by Stephen DeBacker and Paul J. Sally, Jr.Google Scholar
Harris, M. and Taylor, R., The geometry and cohomology of some simple Shimura varieties, Annals of Mathematics Studies, vol. 151 (Princeton University Press, Princeton, NJ, 2001), with an appendix by Vladimir G. Berkovich.Google Scholar
Henniart, G., Une preuve simple des conjectures de Langlands pour GL(n) sur un corps p-adique , Invent. Math. 139 (2000), 439–455.Google Scholar
Hiraga, K. and Saito, H., On L-packets for inner forms of SL n , Mem. Amer. Math. Soc. 215 (2012), vi+97.Google Scholar
Jantzen, C. and Liu, B., The generic dual of p-adic split SO 2n and local Langlands parameters , Israel J. Math. 204 (2014), 199–260.Google Scholar
Jiang, D. and Soudry, D., The local converse theorem for SO (2n + 1) and applications , Ann. of Math. (2) 157 (2003), 743–806.Google Scholar
Jiang, D. and Soudry, D., Generic representations and local Langlands reciprocity law for p-adic SO(2n + 1) , in Contributions to automorphic forms, geometry, and number theory (Johns Hopkins University Press, Baltimore, MD, 2004), 457–519.Google Scholar
Kostant, B., On Whittaker vectors and representation theory , Invent. Math. 48 (1978), 101–184.Google Scholar
Kottwitz, R. E., Rational conjugacy classes in reductive groups , Duke Math. J. 49 (1982), 785–806.Google Scholar
Kottwitz, R. E., Stable trace formula: cuspidal tempered terms , Duke Math. J. 51 (1984), 611–650.Google Scholar
Kottwitz, R. E. and Shelstad, D., Foundations of twisted endoscopy , Astérisque 55 (1999), vi+190.Google Scholar
Kottwitz, R. E. and Shelstad, D., On splitting invariants and sign conventions in endoscopic transfer, Preprint (2012), arXiv:1201.5658.Google Scholar
Labesse, J.-P., Cohomologie, L-groupes et fonctorialité , Compos. Math. 55 (1985), 163–184.Google Scholar
Labesse, J.-P. and Langlands, R. P., L-indistinguishability for SL(2) , Canad. J. Math. 31 (1979), 726–785.Google Scholar
Langlands, R. P., Stable conjugacy: definitions and lemmas , Canad. J. Math. 31 (1979), 700–725.Google Scholar
Langlands, R. P. and Shelstad, D., On the definition of transfer factors , Math. Ann. 278 (1987), 219–271.Google Scholar
Lapid, E. M., On the root number of representations of orthogonal type , Compos. Math. 140 (2004), 274–286.Google Scholar
Lemaire, B., Caractères tordus des représentations admissibles , Astérisque, to appear, Preprint (2013), arXiv:1007.3576.Google Scholar
Liu, B., Genericity of representations of p-adic Sp2n and local Langlands parameters , Canad. J. Math. 63 (2011), 1107–1136.Google Scholar
Mezo, P., Character identities in the twisted endoscopy of real reductive groups , Mem. Amer. Math. Soc. 222 (2013), vi+94.Google Scholar
Milne, J. S. and Shih, K.-Y., Conjugates of Shimura varieties , in Hodge cycles, motives and Shimura varieties, Lecture Notes in Mathematics, vol. 900 (Springer, Berlin–New York, 1982), 280–356.Google Scholar
Mok, C. P., Endoscopic classification of representations of quasi-split unitary groups , Mem. Amer. Math. Soc. 235 (2014), vi+248.Google Scholar
Morel, S., Cohomologie d’intersection des variétés modulaires de Siegel, suite , Compos. Math. 147 (2011), 1671–1740.Google Scholar
Ngô, B. C., Le lemme fondamental pour les algèbres de Lie , Publ. Math. Inst. Hautes Études Sci. (111) (2010), 1–169.Google Scholar
Scholze, P., The local Langlands correspondence for GL n over p-adic fields , Invent. Math. 192 (2013), 663–715.Google Scholar
Shahidi, F., A proof of Langlands’ conjecture on Plancherel measures; complementary series for p-adic groups , Ann. of Math. (2) 132 (1990), 273–330; MR 1070599 (91m:11095).Google Scholar
Shelstad, D., On geometric transfer in real twisted endoscopy , Ann. of Math. (2) 176 (2012), 1919–1985.Google Scholar
Tate, J., Number theoretic background , in Automorphic forms, representations and L-functions (Proc. Symp. Pure Math., Oregon State University, Corvallis, OR, 1977), Part 2, Proceedings of Symposia in Pure Mathematics, vol. XXXIII (American Mathematical Society, Providence, RI, 1979), 3–26.Google Scholar
Waldspurger, J.-L., Une formule des traces locale pour les algèbres de Lie p-adiques , J. reine angew. Math. 465 (1995), 41–99.Google Scholar
Waldspurger, J.-L., Le lemme fondamental implique le transfert , Compos. Math. 105 (1997), 153–236.Google Scholar
Waldspurger, J.-L., Endoscopie et changement de caractéristique , J. Inst. Math. Jussieu 5 (2006), 423–525.Google Scholar
Waldspurger, J.-L., L’endoscopie tordue n’est pas si tordue , Mem. Amer. Math. Soc. 194 (2008), x+261.Google Scholar
Xu, B., L-packets of quasisplit $\text{GSp}(2n)$ and $\text{GO}(2n)$ , Preprint (2015), arXiv:1503.04897.Google Scholar