Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Mathew, Akhil
2022.
Some recent advances in topological Hochschild homology.
Bulletin of the London Mathematical Society,
Vol. 54,
Issue. 1,
p.
1.
Sulyma, Yuri J. F.
2023.
Floor, ceiling, slopes, and K-theory.
Annals of K-Theory,
Vol. 8,
Issue. 3,
p.
331.
Riggenbach, Noah
2023.
K-theory of cuspidal curves over a perfectoid base and formal analogues.
Advances in Mathematics,
Vol. 433,
Issue. ,
p.
109289.
Yi, Xiaomei
Wang, Jiaoping
Wu, Peng
Wang, Guoying
Mo, Lufeng
Lou, Xiongwei
Liang, Hao
Huang, Huahong
Lin, Erpei
Maponde, Brian Tapiwanashe
and
Lv, Chaihui
2023.
AC-UNet: an improved UNet-based method for stem and leaf segmentation in Betula luminifera.
Frontiers in Plant Science,
Vol. 14,
Issue. ,
Zhu, Xiaolong
Zhang, Junhong
Wang, Xinwei
Wang, Hui
and
Lin, Jiewei
2024.
A multi-modal joint attention network for vibro-acoustic fusion diagnosis of engines.
Measurement Science and Technology,
Vol. 35,
Issue. 9,
p.
096104.
Land, Markus
Mathew, Akhil
Meier, Lennart
and
Tamme, Georg
2024.
Purity in chromatically localized algebraic 𝐾-theory.
Journal of the American Mathematical Society,
Keenan, Liam
and
McCandless, Jonas
2024.
A chromatic vanishing result for TR.
Proceedings of the American Mathematical Society,
Gibril, Mohamed Barakat A.
Al-Ruzouq, Rami
Shanableh, Abdallah
Jena, Ratiranjan
Bolcek, Jan
Shafri, Helmi Zulhaidi Mohd
and
Ghorbanzadeh, Omid
2024.
Transformer-based semantic segmentation for large-scale building footprint extraction from very-high resolution satellite images.
Advances in Space Research,
Vol. 73,
Issue. 10,
p.
4937.
Devalapurkar, Sanath K.
and
Mondal, Shubhodip
2025.
p-typical curves on p-adic Tate twists and de Rham–Witt forms.
Advances in Mathematics,
Vol. 479,
Issue. ,
p.
110448.
Riggenbach, Noah
2025.
The S1 assembly map on K-theory and
topological cyclic homology.
Annals of K-Theory,
Vol. 10,
Issue. 3,
p.
447.
Kim, Hyungseop
2025.
Thomason filtration via T(1)-local TC.
Annals of K-Theory,
Vol. 10,
Issue. 1,
p.
1.
Riggenbach, Noah
2025.
K-theory of truncated polynomials.
Mathematische Zeitschrift,
Vol. 310,
Issue. 3,
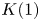 $K(1)$-local
$K(1)$-local 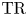 $\mathrm {TR}$
$\mathrm {TR}$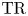 $\mathrm {TR}$ and its
$\mathrm {TR}$ and its 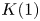 $K(1)$-localization. We prove that after
$K(1)$-localization. We prove that after 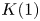 $K(1)$-localization,
$K(1)$-localization, 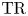 $\mathrm {TR}$ of
$\mathrm {TR}$ of 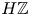 $H\mathbb {Z}$-algebras is a truncating invariant in the Land–Tamme sense, and deduce
$H\mathbb {Z}$-algebras is a truncating invariant in the Land–Tamme sense, and deduce 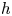 $h$-descent results. We show that for regular rings in mixed characteristic,
$h$-descent results. We show that for regular rings in mixed characteristic, 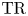 $\mathrm {TR}$ is asymptotically
$\mathrm {TR}$ is asymptotically 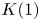 $K(1)$-local, extending results of Hesselholt and Madsen. As an application of these methods and recent advances in the theory of cyclotomic spectra, we construct an analog of Thomason's spectral sequence relating
$K(1)$-local, extending results of Hesselholt and Madsen. As an application of these methods and recent advances in the theory of cyclotomic spectra, we construct an analog of Thomason's spectral sequence relating 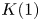 $K(1)$-local
$K(1)$-local 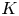 $K$-theory and étale cohomology for
$K$-theory and étale cohomology for 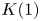 $K(1)$-local
$K(1)$-local 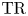 $\mathrm {TR}$.
$\mathrm {TR}$.

