Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Hattori, Shin
2009.
On a ramification bound of torsion semi-stable representations over a local field.
Journal of Number Theory,
Vol. 129,
Issue. 10,
p.
2474.
Caruso, Xavier
and
Savitt, David
2009.
Polygones de Hodge, de Newton et de l’inertie modérée des représentations semi-stables.
Mathematische Annalen,
Vol. 343,
Issue. 4,
p.
773.
Liu, Tong
2010.
A note on lattices in semi-stable representations.
Mathematische Annalen,
Vol. 346,
Issue. 1,
p.
117.
Caruso, Xavier
and
Liu, Tong
2011.
Some bounds for ramification of pn-torsion semi-stable representations.
Journal of Algebra,
Vol. 325,
Issue. 1,
p.
70.
Caruso, Xavier
2011.
F p -représentations semi-stables.
Annales de l'Institut Fourier,
Vol. 61,
Issue. 4,
p.
1683.
Hattori, Shin
2012.
Ramification correspondence of finite flat group schemes over equal and mixed characteristic local fields.
Journal of Number Theory,
Vol. 132,
Issue. 10,
p.
2084.
Liu, Tong
2012.
Lattices in Filtered (φ, N)-modules.
Journal of the Institute of Mathematics of Jussieu,
Vol. 11,
Issue. 3,
p.
659.
Ozeki, Yoshiyasu
2013.
Torsion representations arising from (φ,Gˆ)-modules.
Journal of Number Theory,
Vol. 133,
Issue. 11,
p.
3810.
Caruso, Xavier
2013.
Représentations galoisiennes p-adiques et (φ,τ)-modules.
Duke Mathematical Journal,
Vol. 162,
Issue. 13,
Emerton, Matthew
Gee, Toby
and
Herzig, Florian
2013.
Weight cycling and Serre-type conjectures for unitary groups.
Duke Mathematical Journal,
Vol. 162,
Issue. 9,
Liu, Tong
2014.
The correspondence between Barsotti-Tate groups and Kisin modules when p=2.
Journal de théorie des nombres de Bordeaux,
Vol. 25,
Issue. 3,
p.
661.
Maulik, Davesh
2014.
Supersingular K3 surfaces for large primes.
Duke Mathematical Journal,
Vol. 163,
Issue. 13,
Hattori, Shin
2014.
On lower ramification subgroups and canonical subgroups.
Algebra & Number Theory,
Vol. 8,
Issue. 2,
p.
303.
Emerton, Matthew
and
Gee, Toby
2015.
p-adic Hodge-theoretic properties of étale cohomology with mod pcoefficients, and the cohomology of Shimura varieties.
Algebra & Number Theory,
Vol. 9,
Issue. 5,
p.
1035.
GEE, TOBY
LIU, TONG
and
SAVITT, DAVID
2015.
THE WEIGHT PART OF SERRE’S CONJECTURE FOR .
Forum of Mathematics, Pi,
Vol. 3,
Issue. ,
Liu, Tong
2015.
Filtration associated to torsion semi-stable representations.
Annales de l'Institut Fourier,
Vol. 65,
Issue. 5,
p.
1999.
Kim, Wansu
2015.
The Relative Breuil–Kisin Classification ofp-Divisible Groups and Finite Flat Group Schemes.
International Mathematics Research Notices,
Vol. 2015,
Issue. 17,
p.
8152.
Levin, Brandon
and
Morra, Stefano
2016.
Potentially crystalline deformation rings in the ordinary case.
Annales de l'Institut Fourier,
Vol. 66,
Issue. 5,
p.
1923.
Park, Chol
2017.
Reduction modulo 𝑝 of certain semi-stable representations.
Transactions of the American Mathematical Society,
Vol. 369,
Issue. 8,
p.
5425.
Morra, Stefano
and
Park, Chol
2017.
Serre weights for three-dimensional ordinary Galois representations.
Journal of the London Mathematical Society,
Vol. 96,
Issue. 2,
p.
394.

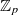 -lattices in semi-stable
-lattices in semi-stable 