Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-26T06:20:55.371Z Has data issue: false hasContentIssue false
  • English
  • Français

On some incomplete theta integrals

Part of: Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  02 August 2019

Jens Funke  and
Stephen Kudla
Jens Funke
Affiliation:
Department of Mathematical Sciences, Durham University, South Road, Durham DH1 3LE, UK email jens.funke@durham.ac.uk
Stephen Kudla
Affiliation:
Department of Mathematics, University of Toronto, 40 St. George Street, Toronto, ON M5S 2E4, Canada email skudla@math.toronto.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we construct indefinite theta series for lattices of arbitrary signature 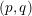$(p,q)$ as ‘incomplete’ theta integrals, that is, by integrating the theta forms constructed by the second author with J. Millson over certain singular 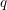$q$-chains in the associated symmetric space 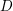$D$. These chains typically do not descend to homology classes in arithmetic quotients of 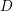$D$, and consequently the theta integrals do not give rise to holomorphic modular forms, but rather to the non-holomorphic completions of certain mock modular forms. In this way we provide a general geometric framework for the indefinite theta series constructed by Zwegers and more recently by Alexandrov, Banerjee, Manschot, and Pioline, Nazaroglu, and Raum. In particular, the coefficients of the mock modular forms are identified with intersection numbers.

Keywords

indefinite theta seriesmock modular forms

MSC classification

Primary: 11F27: Theta series; Weil representation; theta correspondences 11F37: Forms of half-integer weight; nonholomorphic modular forms
Type
Research Article
Information
Compositio Mathematica , Volume 155 , Issue 9 , September 2019 , pp. 1711 - 1746
Copyright
© The Authors 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The second author was supported by an NSERC Discovery Grant.

References

Alexandrov, S., Banerjee, S., Manschot, J. and Pioline, B., Indefinite theta series and generalized error functions , Selecta Math. (N.S.) 24 (2018), 3927–3972.Google Scholar
Bruinier, J. and Funke, J., On two geometric theta lifts , Duke Math. J. 125 (2004), 45–90.Google Scholar
Bruinier, J. and Funke, J., Traces of CM values of modular functions , J. Reine Angew. Math. 594 (2006), 1–33.Google Scholar
Funke, J., Heegner divisors and non-holomorphic modular forms , Compos. Math. 133 (2002), 289–321.Google Scholar
Funke, J. and Kudla, S., Mock modular forms and geometric theta functions for indefinite quadratic forms , J. Phys. A: Math. Theoret. 50 (2017), 404001.Google Scholar
Funke, J. and Millson, J., Cycles in hyperbolic manifolds of non-compact type and Fourier coefficients of Siegel modular forms , Manuscripta Math. 107 (2002), 409–449.Google Scholar
Funke, J. and Millson, J., Spectacle cycles with coefficients and modular forms of half-integral weight , in Arithmetic geometry and automorphic forms, Volume in honor of the 60th birthday of Stephen S. Kudla, Advanced Lectures in Mathematics Series (International Press and the Higher Education Press of China, 2011), 91–154.Google Scholar
Funke, J. and Millson, J., Boundary behavior of special cohomology classes arising from the Weil representation , Jussieu Math. J. 12 (2013), 571–634.Google Scholar
Funke, J. and Millson, J., The geometric theta correspondence for Hilbert modular surfaces , Duke Math. J. 163 (2014), 65–116.Google Scholar
Kudla, S., Holomorphic Siegel modular forms associated to SO (n, 1) , Math. Ann. 256 (1981), 517–534.Google Scholar
Kudla, S., A note on Zwegers’ theta functions, Preprint (2013).Google Scholar
Kudla, S., Theta integrals and generalized error functions , Manuscripta Math. 155 (2018), 303–333.Google Scholar
Kudla, S. and Millson, J., The theta correspondence and harmonic forms I , Math. Ann. 274 (1986), 353–378.Google Scholar
Kudla, S. and Millson, J., The theta correspondence and harmonic forms II , Math. Ann. 277 (1987), 267–314.Google Scholar
Kudla, S. and Millson, J., Intersection numbers of cycles on locally symmetric spaces and Fourier coefficients of holomorphic modular forms in several complex variables , Publ. Math. Inst. Hautes Études Sci. 71 (1990), 121–172.Google Scholar
Livinskyi, I., On the integrals of the Kudla–Millson theta series, PhD thesis, University of Toronto (2016).Google Scholar
Massey, W. S., A basic course in algebraic topology, Graduate Texts in Mathematics, vol. 127 (Springer, New York, 1991).Google Scholar
Nazaroglu, C., r-tuple error functions and indefinite theta series of higher depth , Commun. Number Theory Phys. 12 (2018), 581–608.Google Scholar
Shintani, T., On construction of holomorphic cusp forms of half-integral weight , Nagoya Math. J. 58 (1975), 83–126.Google Scholar
Vignéras, M.-F., Séries theta des formes quadratiques indéfinies , in Modular functions of one variable VI, Lecture Notes in Mathematics, vol. 627 (Springer, Berlin, 1977), 227–239.Google Scholar
Westerholt-Raum, M., Indefinite theta series on cones, Preprint (2016), arXiv:1608.08874v2.Google Scholar
Zagier, D., Ramanujan’s mock theta functions and their applications (after Zwegers and Ono-Bringmann) , in Séminaire Bourbaki, Vol. 2007/2008, Astérisque, vol. 326 (Société Mathématique de France, Paris, 2010); Exp. No. 986, vii–viii, 143–164.Google Scholar
Zwegers, S. P., Mock theta functions, PhD thesis, University of Utrecht (2002), https://dspace.library.uu.nl/handle/1874/878.Google Scholar