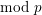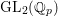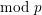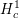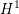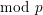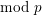Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Chojecki, Przemysław
2017.
On non-abelian Lubin-Tate theory and analytic cohomology.
Proceedings of the American Mathematical Society,
Vol. 146,
Issue. 2,
p.
459.
Banerjee, Debargha
and
Rai, Vivek
2024.
Towards a mod-p Lubin–Tate theory for GL2 over totally real fields.
International Journal of Number Theory,
Vol. 20,
Issue. 01,
p.
199.