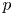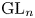1. Introduction
We study the smooth representation theory of a split reductive group ![]() $G$ over a non-archimedean local field
$G$ over a non-archimedean local field ![]() $F$. The classification of the irreducible smooth
$F$. The classification of the irreducible smooth ![]() $G$-representations is one of the main objectives of the local Langlands program. One aims to parametrize these representations by so-called L-parameters, together with some additional datum (a representation of a finite group associated to the L-parameter). Such a parametrization has been established in the case of
$G$-representations is one of the main objectives of the local Langlands program. One aims to parametrize these representations by so-called L-parameters, together with some additional datum (a representation of a finite group associated to the L-parameter). Such a parametrization has been established in the case of ![]() ${\rm GL}_n(F)$. For split reductive groups it has been established by Kazhdan and Lusztig for those irreducible smooth representations of
${\rm GL}_n(F)$. For split reductive groups it has been established by Kazhdan and Lusztig for those irreducible smooth representations of ![]() $G$ that have a non-trivial fixed vector under an Iwahori subgroup
$G$ that have a non-trivial fixed vector under an Iwahori subgroup ![]() $I\subset G$ (see [Reference Kazhdan and LusztigKL87]). In this case an L-parameter just becomes a conjugacy class of
$I\subset G$ (see [Reference Kazhdan and LusztigKL87]). In this case an L-parameter just becomes a conjugacy class of ![]() $(\varphi,N)$, where
$(\varphi,N)$, where ![]() $\varphi$ is a semi-simple element of the Langlands dual group
$\varphi$ is a semi-simple element of the Langlands dual group ![]() $\check G$, and
$\check G$, and ![]() $N\in \operatorname {Lie}\check G$, satisfying
$N\in \operatorname {Lie}\check G$, satisfying ![]() ${\rm Ad}(\varphi )(N)=q^{-1}N$. Here
${\rm Ad}(\varphi )(N)=q^{-1}N$. Here ![]() $q$ is the number of elements of the residue field of
$q$ is the number of elements of the residue field of ![]() $F$. This parametrization depends on an additional choice, called a Whittaker datum.
$F$. This parametrization depends on an additional choice, called a Whittaker datum.
In this paper we formulate a conjecture that lifts the Langlands classification to a fully faithful embedding of the category ![]() ${\rm Rep}(G)$ of smooth
${\rm Rep}(G)$ of smooth ![]() $G$-representations (on vector spaces over a field
$G$-representations (on vector spaces over a field ![]() $C$ of characteristic zero) to the category of quasi-coherent sheaves on the stack of L-parameters. It turns out that this conjecture has to be formulated at the level of derived categories. As one of the main tools in the study of smooth representations is parabolic induction, we require this fully faithful embedding to be compatible with parabolic induction in a precise sense. Moreover, the conjectured functor should depend on the choice of a Whittaker datum. Similar conjectures and results where obtained by Ben-Zvi, Chen, Helm and Nadler [Reference Ben-Zvi, Chen, Helm and NadlerBCHN20] and Zhu [Reference ZhuZhu20]. The conjectures stated here can also be regarded as a special case of the conjectural geometrization of the local Langlands correspondence of Fargues and Scholze [Reference Fargues and ScholzeFS21].
$C$ of characteristic zero) to the category of quasi-coherent sheaves on the stack of L-parameters. It turns out that this conjecture has to be formulated at the level of derived categories. As one of the main tools in the study of smooth representations is parabolic induction, we require this fully faithful embedding to be compatible with parabolic induction in a precise sense. Moreover, the conjectured functor should depend on the choice of a Whittaker datum. Similar conjectures and results where obtained by Ben-Zvi, Chen, Helm and Nadler [Reference Ben-Zvi, Chen, Helm and NadlerBCHN20] and Zhu [Reference ZhuZhu20]. The conjectures stated here can also be regarded as a special case of the conjectural geometrization of the local Langlands correspondence of Fargues and Scholze [Reference Fargues and ScholzeFS21].
The conjecture can be made more precise in the case of the principal Bernstein block ![]() ${\rm Rep}_{[T,1]}(G)$ of
${\rm Rep}_{[T,1]}(G)$ of ![]() ${\rm Rep}(G)$, that is, the block containing the trivial representation. This block coincides with the full subcategory
${\rm Rep}(G)$, that is, the block containing the trivial representation. This block coincides with the full subcategory ![]() ${\rm Rep}^IG$ of smooth
${\rm Rep}^IG$ of smooth ![]() $G$-representations generated by their
$G$-representations generated by their ![]() $I$-fixed vectors for a choice of an Iwahori subgroup
$I$-fixed vectors for a choice of an Iwahori subgroup ![]() $I\subset G$. As
$I\subset G$. As ![]() ${\rm Rep}^IG$ is equivalent to the category of modules over the Iwahori–Hecke algebra the conjecture comes down to a conjecture about the derived category of the Iwahori–Hecke algebra.
${\rm Rep}^IG$ is equivalent to the category of modules over the Iwahori–Hecke algebra the conjecture comes down to a conjecture about the derived category of the Iwahori–Hecke algebra.
In the main part of the paper we investigate the conjecture in the case of ![]() $G={\rm GL}_n(F)$ and the principal block by relating it to the construction of a family of
$G={\rm GL}_n(F)$ and the principal block by relating it to the construction of a family of ![]() $G$-representations interpolating the (modified) local Langlands correspondence, following the work of Emerton and Helm [Reference Emerton and HelmEH14].
$G$-representations interpolating the (modified) local Langlands correspondence, following the work of Emerton and Helm [Reference Emerton and HelmEH14].
We describe the conjecture and our results in more detail. Fix a finite extension ![]() $F$ of
$F$ of ![]() $\mathbb {Q}_p$, or of
$\mathbb {Q}_p$, or of ![]() $\mathbb {F}_p(\!(t)\!)$. Let
$\mathbb {F}_p(\!(t)\!)$. Let ![]() $\mathbb {G}$ be a split reductive group over
$\mathbb {G}$ be a split reductive group over ![]() $F$ and write
$F$ and write ![]() $G=\mathbb {G}(F)$. We fix a field
$G=\mathbb {G}(F)$. We fix a field ![]() $C$ of characteristic zero and shall always assume that
$C$ of characteristic zero and shall always assume that ![]() $C$ contains a square root
$C$ contains a square root ![]() $q^{1/2}$ of
$q^{1/2}$ of ![]() $q$. We denote by
$q$. We denote by ![]() $\check G$ the dual group of
$\check G$ the dual group of ![]() $G$, considered as a reductive group over
$G$, considered as a reductive group over ![]() $C$. More generally, for every parabolic (or Levi)
$C$. More generally, for every parabolic (or Levi) ![]() $\mathbb {P}$ (or
$\mathbb {P}$ (or ![]() $\mathbb {M}$) of
$\mathbb {M}$) of ![]() $\mathbb {G}$ we will write
$\mathbb {G}$ we will write ![]() $P=\mathbb {P}(F)$ (respectively,
$P=\mathbb {P}(F)$ (respectively, ![]() $M=\mathbb {M}(F)$) for its group of
$M=\mathbb {M}(F)$) for its group of ![]() $F$-valued points and
$F$-valued points and ![]() $\check P$ (respectively,
$\check P$ (respectively, ![]() $\check M$) for its dual group over
$\check M$) for its dual group over ![]() $C$. For each parabolic subgroup
$C$. For each parabolic subgroup ![]() $P\subset G$ with Levi
$P\subset G$ with Levi ![]() $M$ (normalized) parabolic induction defines a functor
$M$ (normalized) parabolic induction defines a functor ![]() $\iota _{\overline {P}}^G$ from
$\iota _{\overline {P}}^G$ from ![]() $M$-representations to
$M$-representations to ![]() $G$-representations.
$G$-representations.
On the other hand, we denote by ![]() $X_{\check G}^{\rm WD}$ the space of Weil–Deligne representations with values in
$X_{\check G}^{\rm WD}$ the space of Weil–Deligne representations with values in ![]() $\check G$, that is, the space whose
$\check G$, that is, the space whose ![]() $C$-valued points are pairs
$C$-valued points are pairs ![]() $(\rho,N)$ consisting of a smooth representation
$(\rho,N)$ consisting of a smooth representation ![]() $W_F\rightarrow \check G(C)$ of the Weil group
$W_F\rightarrow \check G(C)$ of the Weil group ![]() $W_F$ of
$W_F$ of ![]() $F$ and
$F$ and ![]() $N\in \operatorname {Lie} \check G$ satisfying the usual relation
$N\in \operatorname {Lie} \check G$ satisfying the usual relation
where ![]() $\|-\|:W_F\rightarrow \mathbb {Z}$ is the projection. We shall write
$\|-\|:W_F\rightarrow \mathbb {Z}$ is the projection. We shall write ![]() $[X_{\check G}^{\rm WD}/\check G]$ for the stack quotient by the obvious
$[X_{\check G}^{\rm WD}/\check G]$ for the stack quotient by the obvious ![]() $\check G$-action.
$\check G$-action.
Let us write ![]() $\mathcal {Z}(\check G)$ for the global sections of the structure sheaf on
$\mathcal {Z}(\check G)$ for the global sections of the structure sheaf on ![]() $[X_{\check G}^{\rm WD}/\check G]$, or equivalently the coordinate ring of the geometric invariant theory (GIT) quotient
$[X_{\check G}^{\rm WD}/\check G]$, or equivalently the coordinate ring of the geometric invariant theory (GIT) quotient ![]() $X_{\check G}^{\rm WD}/\hspace {-.1cm}/\check G$. Moreover, we write
$X_{\check G}^{\rm WD}/\hspace {-.1cm}/\check G$. Moreover, we write ![]() $\mathfrak {Z}(G)$ for the Bernstein center of
$\mathfrak {Z}(G)$ for the Bernstein center of ![]() ${\rm Rep}(G)$. With this notation we state the following conjecture. For the sake of brevity we state the conjecture in a vague form and refer to the body of the paper for a more precise formulation.
${\rm Rep}(G)$. With this notation we state the following conjecture. For the sake of brevity we state the conjecture in a vague form and refer to the body of the paper for a more precise formulation.
Conjecture 1.1 There exist the following data.
(i) For each
 $(\mathbb {G},\mathbb {B},\mathbb {T},\psi )$ consisting of a reductive group
$(\mathbb {G},\mathbb {B},\mathbb {T},\psi )$ consisting of a reductive group  $\mathbb {G}$, a Borel subgroup
$\mathbb {G}$, a Borel subgroup  $\mathbb {B}$, a split maximal torus
$\mathbb {B}$, a split maximal torus  $\mathbb {T}\subset \mathbb {B}$, and a (conjugacy class of a) generic character
$\mathbb {T}\subset \mathbb {B}$, and a (conjugacy class of a) generic character  $\psi :N\rightarrow C^\times$, there exists an exact and fully faithful functor
$\psi :N\rightarrow C^\times$, there exists an exact and fully faithful functor
 \[ \mathcal{R}_G^\psi:{\bf D}^+({\rm Rep}(G))\longrightarrow {\bf D}^+_{\rm QCoh}([X^{\rm WD}_{\check G}/\check G]). \]
\[ \mathcal{R}_G^\psi:{\bf D}^+({\rm Rep}(G))\longrightarrow {\bf D}^+_{\rm QCoh}([X^{\rm WD}_{\check G}/\check G]). \]
(ii) For
 $(\mathbb {G},\mathbb {B},\mathbb {T},\psi )$ as in (i) and a parabolic subgroup
$(\mathbb {G},\mathbb {B},\mathbb {T},\psi )$ as in (i) and a parabolic subgroup  $\mathbb {P}\subset \mathbb {G}$ containing
$\mathbb {P}\subset \mathbb {G}$ containing  $\mathbb {B}$ we denote by
$\mathbb {B}$ we denote by  $\mathbb {M}$ the Levi quotient of
$\mathbb {M}$ the Levi quotient of  $\mathbb {P}$. Then the functors
$\mathbb {P}$. Then the functors  $\mathcal {R}^\psi _G$ and
$\mathcal {R}^\psi _G$ and  $\mathcal {R}_M^{\psi _M}$ satisfy a compatibility with parabolic induction
$\mathcal {R}_M^{\psi _M}$ satisfy a compatibility with parabolic induction  $\iota _{\overline {P}}^G$. Here
$\iota _{\overline {P}}^G$. Here  $\psi _M$ is the restriction of
$\psi _M$ is the restriction of  $\psi$ to the unipotent radical of the Borel
$\psi$ to the unipotent radical of the Borel  $B_M$ of
$B_M$ of  $M$ via the splitting
$M$ via the splitting  $\mathbb {M}\rightarrow \mathbb {P}$ defined by
$\mathbb {M}\rightarrow \mathbb {P}$ defined by  $\mathbb {T}$.
$\mathbb {T}$.
These data satisfy the following conditions.
(a) If
 $\mathbb {G}=\mathbb {T}$ is a split torus, then
$\mathbb {G}=\mathbb {T}$ is a split torus, then  $\mathcal {R}_T=\mathcal {R}_T^{\psi }$ is induced by the equivalence
given by local class field theory.
$\mathcal {R}_T=\mathcal {R}_T^{\psi }$ is induced by the equivalence
given by local class field theory. \[ {\rm Rep}(T)\cong {\rm QCoh}(X_{\check T}^{\rm WD}) \]
\[ {\rm Rep}(T)\cong {\rm QCoh}(X_{\check T}^{\rm WD}) \]
(b) Let
 $(\mathbb {G},\mathbb {B},\mathbb {T},\psi )$ be as in (i). The morphism
$(\mathbb {G},\mathbb {B},\mathbb {T},\psi )$ be as in (i). The morphism  $\mathcal {Z}(\check G)\rightarrow \mathfrak {Z}(G)$ defined by full faithfulness of
$\mathcal {Z}(\check G)\rightarrow \mathfrak {Z}(G)$ defined by full faithfulness of  $\mathcal {R}_G^\psi$ is independent of the choice of
$\mathcal {R}_G^\psi$ is independent of the choice of  $\psi$ and induces a surjection
$\psi$ and induces a surjection
 \[ \omega_G:\left\{\begin{array}{@{}c@{}} \text{Bernstein components}\\ \text{of}\ {\rm Rep} (G) \end{array}\right\}\longrightarrow\left\{\begin{array}{@{}c@{}} \text{connected components}\\ \text{of}\ X_{\check G}^{\rm WD} \end{array}\right\}. \]
\[ \omega_G:\left\{\begin{array}{@{}c@{}} \text{Bernstein components}\\ \text{of}\ {\rm Rep} (G) \end{array}\right\}\longrightarrow\left\{\begin{array}{@{}c@{}} \text{connected components}\\ \text{of}\ X_{\check G}^{\rm WD} \end{array}\right\}. \]
(c) For
 $(\mathbb {G},\mathbb {B},\mathbb {T},\psi )$ as in (i) there is an isomorphism
$(\mathbb {G},\mathbb {B},\mathbb {T},\psi )$ as in (i) there is an isomorphism
 \[ R_G^\psi((\operatorname{c-ind}_N^G\psi))\cong \mathcal{O}_{[X^{\rm WD}_{\check G}/\check G]}. \]
\[ R_G^\psi((\operatorname{c-ind}_N^G\psi))\cong \mathcal{O}_{[X^{\rm WD}_{\check G}/\check G]}. \]
In this paper we mainly focus on the conjecture in the case of the principal block of ![]() ${\rm Rep}(G)$. If
${\rm Rep}(G)$. If ![]() $T\subset G$ is a split maximal torus, we write
$T\subset G$ is a split maximal torus, we write ![]() ${\rm Rep}_{[T,1]}(G)$ for the Bernstein block of those representations
${\rm Rep}_{[T,1]}(G)$ for the Bernstein block of those representations ![]() $\pi$ such that all irreducible subquotients of
$\pi$ such that all irreducible subquotients of ![]() $\pi$ are subquotients of a representations induced from an unramified
$\pi$ are subquotients of a representations induced from an unramified ![]() $T$-representation. Then parabolic induction restricts to a functor
$T$-representation. Then parabolic induction restricts to a functor
for any choice of maximal split tori ![]() $T\subset G$ and
$T\subset G$ and ![]() $T_M\subset M$ (as the categories do not depend on these choices).
$T_M\subset M$ (as the categories do not depend on these choices).
On the other hand, we denote by ![]() $X_{\check G}=\{(\varphi,N)\in \check G\times \operatorname {Lie}\check G\mid {\rm Ad}(\varphi )(N)=q^{-1}N\}$ the space of L-parameters (corresponding to the representations in the principal block) and write
$X_{\check G}=\{(\varphi,N)\in \check G\times \operatorname {Lie}\check G\mid {\rm Ad}(\varphi )(N)=q^{-1}N\}$ the space of L-parameters (corresponding to the representations in the principal block) and write ![]() $[X_{\check G}/\check G]$ for the stack quotient by the action of
$[X_{\check G}/\check G]$ for the stack quotient by the action of ![]() $\check G$ induced by conjugation. We obtain similar spaces
$\check G$ induced by conjugation. We obtain similar spaces ![]() $[X_{\check P}/\check P]$ etc. for parabolic subgroups
$[X_{\check P}/\check P]$ etc. for parabolic subgroups ![]() $P\subset G$ (or their Levi quotients). If
$P\subset G$ (or their Levi quotients). If ![]() $T$ is a (maximal split) torus, then
$T$ is a (maximal split) torus, then ![]() $X_{\check T}$ is just the dual torus
$X_{\check T}$ is just the dual torus ![]() $\check T$.
$\check T$.
In this case the relation between the Bernstein center ![]() $\mathfrak {Z}_G=\mathfrak {Z}_{[T,1]}(G)$ of the category
$\mathfrak {Z}_G=\mathfrak {Z}_{[T,1]}(G)$ of the category ![]() ${\rm Rep}_{[T,1]}(G)$ and the GIT quotient
${\rm Rep}_{[T,1]}(G)$ and the GIT quotient ![]() $X_{\check G}/\hspace {-.1cm}/\check G$ can be made precise: the center
$X_{\check G}/\hspace {-.1cm}/\check G$ can be made precise: the center ![]() $\mathfrak {Z}_G$ can naturally be identified with the functions on the adjoint quotient of
$\mathfrak {Z}_G$ can naturally be identified with the functions on the adjoint quotient of ![]() $\check G$ and hence
$\check G$ and hence ![]() $\mathfrak {Z}_G$ acts on categories of modules over
$\mathfrak {Z}_G$ acts on categories of modules over ![]() $X_{\check G}$ as well as on
$X_{\check G}$ as well as on ![]() ${\rm Rep}_{[T,1]}(G)$. The following conjecture is a slightly more precise version of Conjecture 1.1 in the case of the block
${\rm Rep}_{[T,1]}(G)$. The following conjecture is a slightly more precise version of Conjecture 1.1 in the case of the block ![]() ${\rm Rep}_{[T,1]}(G)$. Equivalently, the conjecture can be interpreted as a conjecture about the derived category of the Iwahori–Hecke algebra, and we shall take this point of view in the last part of the paper when we discuss the case of
${\rm Rep}_{[T,1]}(G)$. Equivalently, the conjecture can be interpreted as a conjecture about the derived category of the Iwahori–Hecke algebra, and we shall take this point of view in the last part of the paper when we discuss the case of ![]() ${\rm GL}_n$. In the case of modules over an affine Hecke algebra (where
${\rm GL}_n$. In the case of modules over an affine Hecke algebra (where ![]() $q$ is an invertible indeterminate) a similar conjectureFootnote 1 is due to Ben-Zvi et al. [Reference Ben-Zvi, Chen, Helm and NadlerBCHN20] and Zhu [Reference ZhuZhu20].
$q$ is an invertible indeterminate) a similar conjectureFootnote 1 is due to Ben-Zvi et al. [Reference Ben-Zvi, Chen, Helm and NadlerBCHN20] and Zhu [Reference ZhuZhu20].
Conjecture 1.2 There exist the following data.
(i) For each
 $(\mathbb {G},\mathbb {B},\mathbb {T},\psi )$ consisting of a reductive group
$(\mathbb {G},\mathbb {B},\mathbb {T},\psi )$ consisting of a reductive group  $\mathbb {G}$, a Borel subgroup
$\mathbb {G}$, a Borel subgroup  $\mathbb {B}$, a maximal split torus
$\mathbb {B}$, a maximal split torus  $\mathbb {T}\subset \mathbb {B}$ and a (conjugacy class of a) generic character
$\mathbb {T}\subset \mathbb {B}$ and a (conjugacy class of a) generic character  $\psi :N\rightarrow C^\times$, there exists an exact and fully faithful
$\psi :N\rightarrow C^\times$, there exists an exact and fully faithful  $\mathfrak {Z}_G$-linear functor
$\mathfrak {Z}_G$-linear functor
 \[ R_G^\psi:{\bf D}^+({\rm Rep}_{[T,1]}(G))\longrightarrow {\bf D}^+_{\rm QCoh}([X_{\check G}/\check G]). \]
\[ R_G^\psi:{\bf D}^+({\rm Rep}_{[T,1]}(G))\longrightarrow {\bf D}^+_{\rm QCoh}([X_{\check G}/\check G]). \]
(ii) For
 $(\mathbb {G},\mathbb {B},\mathbb {T},\psi )$ as in (i) and each parabolic subgroup
$(\mathbb {G},\mathbb {B},\mathbb {T},\psi )$ as in (i) and each parabolic subgroup  $\mathbb {P}\subset \mathbb {G}$ containing
$\mathbb {P}\subset \mathbb {G}$ containing  $\mathbb {B}$, there exists a natural
$\mathbb {B}$, there exists a natural  $\mathfrak {Z}_{G}$-linear isomorphism
of functors
$\mathfrak {Z}_{G}$-linear isomorphism
of functors \[ \xi_{P}^{G}:R_{G}^\psi\circ \iota_{\overline{P}}^{G}\longrightarrow (R\beta_{\ast}\circ L\alpha^\ast)\circ R_{M}^{\psi_M} \]
\[ \xi_{P}^{G}:R_{G}^\psi\circ \iota_{\overline{P}}^{G}\longrightarrow (R\beta_{\ast}\circ L\alpha^\ast)\circ R_{M}^{\psi_M} \]
 ${\bf D}^+({\rm Rep}_{[T_M,1]}M)\rightarrow {\bf D}^+_{\rm QCoh}([X_{\check G}/\check G])$ such that the various
${\bf D}^+({\rm Rep}_{[T_M,1]}M)\rightarrow {\bf D}^+_{\rm QCoh}([X_{\check G}/\check G])$ such that the various  $\xi _{P}^{G}$ are compatible (in a precise sense). Here
$\xi _{P}^{G}$ are compatible (in a precise sense). Here  $\mathbb {M}$ is the Levi quotient of
$\mathbb {M}$ is the Levi quotient of  $\mathbb {P}$, the character
$\mathbb {P}$, the character  $\psi _M$ is the restriction of
$\psi _M$ is the restriction of  $\psi$ to the unipotent radical of
$\psi$ to the unipotent radical of  $B_M=B\cap M$ (using a splitting
$B_M=B\cap M$ (using a splitting  $M\hookrightarrow P$ of
$M\hookrightarrow P$ of  $P\rightarrow M$), and
are the morphisms on stacks induced by the natural maps
$P\rightarrow M$), and
are the morphisms on stacks induced by the natural maps \begin{align*} & \alpha:[X_{\check P}/\check P]\longrightarrow [X_{\check M}/\check M], \\ & \beta:[X_{\check P}/\check P]\longrightarrow [X_{\check G}/\check G] \end{align*}
\begin{align*} & \alpha:[X_{\check P}/\check P]\longrightarrow [X_{\check M}/\check M], \\ & \beta:[X_{\check P}/\check P]\longrightarrow [X_{\check G}/\check G] \end{align*}
 $\check P\rightarrow \check M$ and
$\check P\rightarrow \check M$ and  $\check P\rightarrow \check G$.
$\check P\rightarrow \check G$.
For a maximal split torus ![]() $T$ the functor
$T$ the functor ![]() $R_T=R_T^{\psi _T}$ is induced by the identification
$R_T=R_T^{\psi _T}$ is induced by the identification
where ![]() $T^\circ \subset T$ is the maximal compact subgroup. Moreover, for
$T^\circ \subset T$ is the maximal compact subgroup. Moreover, for ![]() $(\mathbb {G},\mathbb {B},\mathbb {T},\psi )$ as in (i) there is an isomorphism
$(\mathbb {G},\mathbb {B},\mathbb {T},\psi )$ as in (i) there is an isomorphism
In fact it turns out that in the formulation of the conjecture the stack ![]() $[X_{\check P}/\check P]$ has to be replaced by a derived variant. Again, we refer to the body of the paper for details and a more precise formulation of the conjecture.
$[X_{\check P}/\check P]$ has to be replaced by a derived variant. Again, we refer to the body of the paper for details and a more precise formulation of the conjecture.
In the case ![]() $G={\rm GL}_n(F)$ we consider a candidate for the conjectured functor. Emerton and Helm [Reference Emerton and HelmEH14] have suggested (in the context of
$G={\rm GL}_n(F)$ we consider a candidate for the conjectured functor. Emerton and Helm [Reference Emerton and HelmEH14] have suggested (in the context of ![]() $\ell$-adic deformation rings rather than the stack
$\ell$-adic deformation rings rather than the stack ![]() $[X_{\check G}/\check G]$) the existence of a family
$[X_{\check G}/\check G]$) the existence of a family ![]() $\mathcal {V}_G$ of smooth
$\mathcal {V}_G$ of smooth ![]() $G$-representations on
$G$-representations on ![]() $[X_{\check G}/\check G]$ that interpolates the modified local Langlands correspondence. A candidate for the family
$[X_{\check G}/\check G]$ that interpolates the modified local Langlands correspondence. A candidate for the family ![]() $\mathcal {V}_G$ was constructed by Helm in [Reference HelmHel16]. The modified local Langlands correspondence assigns to
$\mathcal {V}_G$ was constructed by Helm in [Reference HelmHel16]. The modified local Langlands correspondence assigns to ![]() $(\varphi,N)\in X_{\check G}(C)$ a certain representation
$(\varphi,N)\in X_{\check G}(C)$ a certain representation ![]() ${\rm LL^{mod}}(\varphi,N)$ that is indecomposable, induced from a parabolic subgroup, has a unique irreducible subrepresentation which is a generic representation, and its unique irreducible quotient is the representation
${\rm LL^{mod}}(\varphi,N)$ that is indecomposable, induced from a parabolic subgroup, has a unique irreducible subrepresentation which is a generic representation, and its unique irreducible quotient is the representation ![]() ${\rm LL}(\varphi,N)$ associated to
${\rm LL}(\varphi,N)$ associated to ![]() $(\varphi,N)$ by the local Langlands correspondence. In the context of modules over the Iwahori–Hecke algebra
$(\varphi,N)$ by the local Langlands correspondence. In the context of modules over the Iwahori–Hecke algebra ![]() $\mathcal {H}_G$ the
$\mathcal {H}_G$ the ![]() ${\mathcal {H}_G}$-modules corresponding to the representations
${\mathcal {H}_G}$-modules corresponding to the representations ![]() ${\rm LL^{mod}}(\varphi,N)$ are often referred to as the standard modules.
${\rm LL^{mod}}(\varphi,N)$ are often referred to as the standard modules.
We conjecture that, in the ![]() ${\rm GL}_n$ case, the functor
${\rm GL}_n$ case, the functor ![]() $R_G=R_G^\psi$ should be given by the derived tensor product with
$R_G=R_G^\psi$ should be given by the derived tensor product with ![]() $\mathcal {V}_G$ (we omit the superscript
$\mathcal {V}_G$ (we omit the superscript ![]() $\psi$ from the notation, as in the case of
$\psi$ from the notation, as in the case of ![]() ${\rm GL}_n$ there is a unique Whittaker datum). For the precise formulation it is more convenient to pass from
${\rm GL}_n$ there is a unique Whittaker datum). For the precise formulation it is more convenient to pass from ![]() $G$-representations to modules over the Iwahori–Hecke algebra
$G$-representations to modules over the Iwahori–Hecke algebra ![]() $\mathcal {H}_G$. The family of
$\mathcal {H}_G$. The family of ![]() $\mathcal {H}_G$-modules associated to
$\mathcal {H}_G$-modules associated to ![]() $\mathcal {V}_G$ by taking
$\mathcal {V}_G$ by taking ![]() $I$-invariants is in fact a
$I$-invariants is in fact a ![]() $\mathcal {H}_G\otimes _{\mathfrak {Z}_G}\mathcal {O}_{[X_{\check G}/\check G]}$-module
$\mathcal {H}_G\otimes _{\mathfrak {Z}_G}\mathcal {O}_{[X_{\check G}/\check G]}$-module ![]() $\mathcal {M}_G$ that is coherent as an
$\mathcal {M}_G$ that is coherent as an ![]() $\mathcal {O}_{[X_{\check G}/\check G]}$-module.
$\mathcal {O}_{[X_{\check G}/\check G]}$-module.
We consider the functor
mapping ![]() $\pi$ to
$\pi$ to ![]() ${}^t\pi \otimes ^L_{\mathcal {H}_G}\mathcal {M}_G$. Here
${}^t\pi \otimes ^L_{\mathcal {H}_G}\mathcal {M}_G$. Here ![]() ${}^t\pi$ is
${}^t\pi$ is ![]() $\pi$ considered as a right module over
$\pi$ considered as a right module over ![]() $\mathcal {H}_G$ by means of the standard involution
$\mathcal {H}_G$ by means of the standard involution ![]() $\mathcal {H}_G\cong \mathcal {H}_G^{\rm op}$, and we point out that the derived tensor product can easily be made explicit, as
$\mathcal {H}_G\cong \mathcal {H}_G^{\rm op}$, and we point out that the derived tensor product can easily be made explicit, as ![]() $\mathcal {H}_G$ has finite global dimension. Every (standard) Levi subgroup of
$\mathcal {H}_G$ has finite global dimension. Every (standard) Levi subgroup of ![]() ${\rm GL}_n(F)$ is a product of some
${\rm GL}_n(F)$ is a product of some ![]() ${\rm GL}_m(F)$, and hence we can construct similar functors
${\rm GL}_m(F)$, and hence we can construct similar functors
for every Levi ![]() $M$. Over a certain (open and dense) regular locus
$M$. Over a certain (open and dense) regular locus ![]() $X_{\check G}^{\rm reg}$ of
$X_{\check G}^{\rm reg}$ of ![]() $X_{\check G}$ (see § 2.1 for the definition) we can relate the functor
$X_{\check G}$ (see § 2.1 for the definition) we can relate the functor ![]() $R_G$ to Conjecture 1.2 as follows.
$R_G$ to Conjecture 1.2 as follows.
Theorem 1.3 Let ![]() $\mathbb {G}={\rm GL}_n$. For each parabolic
$\mathbb {G}={\rm GL}_n$. For each parabolic ![]() $\mathbb {P}\subset \mathbb {G}$ with Levi
$\mathbb {P}\subset \mathbb {G}$ with Levi ![]() $\mathbb {M}$ the restriction of (1.2) to the regular locus is a
$\mathbb {M}$ the restriction of (1.2) to the regular locus is a ![]() $\mathfrak {Z}_M$-linear functor
$\mathfrak {Z}_M$-linear functor
satisfying compatibility with parabolic induction as in Conjecture 1.2. Moreover,
for any choice of a generic character ![]() $\psi :N\rightarrow C^\times$ of the unipotent radical
$\psi :N\rightarrow C^\times$ of the unipotent radical ![]() $N$ of a Borel subgroup
$N$ of a Borel subgroup ![]() $B\subset {\rm GL}_n(F)$.
$B\subset {\rm GL}_n(F)$.
In the case of ![]() ${\rm GL}_2(F)$ we can also control the situation for non-regular
${\rm GL}_2(F)$ we can also control the situation for non-regular ![]() $(\varphi,N)$ and prove full faithfulness.
$(\varphi,N)$ and prove full faithfulness.
Theorem 1.4 Let ![]() $G={\rm GL}_2(F)$ and
$G={\rm GL}_2(F)$ and ![]() $T\subset B\subset G$ denote the standard maximal torus and the standard Borel, respectively. The functors
$T\subset B\subset G$ denote the standard maximal torus and the standard Borel, respectively. The functors ![]() $R_G$ and
$R_G$ and ![]() $R_T$ defined by (1.1) are fully faithful and there is a natural
$R_T$ defined by (1.1) are fully faithful and there is a natural ![]() $\mathfrak {Z}_G$-linear isomorphism
$\mathfrak {Z}_G$-linear isomorphism
where ![]() $\alpha$ and
$\alpha$ and ![]() $\beta$ are defined as in Conjecture 1.2(ii).
$\beta$ are defined as in Conjecture 1.2(ii).
We finally return to ![]() ${\rm GL}_n$ for arbitrary
${\rm GL}_n$ for arbitrary ![]() $n$, but restrict to the case of
$n$, but restrict to the case of ![]() $(\varphi,N)$ with
$(\varphi,N)$ with ![]() $\varphi$ regular semi-simple. Over the regular semi-simple locus the situation in fact can be controlled very explicitly and we are able to compute examples. Given
$\varphi$ regular semi-simple. Over the regular semi-simple locus the situation in fact can be controlled very explicitly and we are able to compute examples. Given ![]() $(\varphi,N)\in X_{\check G}(C)$ with regular semi-simple
$(\varphi,N)\in X_{\check G}(C)$ with regular semi-simple ![]() $\varphi$, we write
$\varphi$, we write ![]() $X_{\check G,[\varphi,N]}$ for the Zariski closure of its
$X_{\check G,[\varphi,N]}$ for the Zariski closure of its ![]() $\check G$-orbit.
$\check G$-orbit.
Theorem 1.5 Let ![]() $(\varphi,N)\in X_{\check G}(C)$ and assume that
$(\varphi,N)\in X_{\check G}(C)$ and assume that ![]() $\varphi$ is regular semi-simple. Then
$\varphi$ is regular semi-simple. Then
Remark 1.6 We expect a similar statement in general (see Remark 3.3(b) for a statement for more general reductive groups, and remark (d) in § 4.7 for the case of ![]() ${\rm GL}_n$ and points
${\rm GL}_n$ and points ![]() $(\varphi,N)$ where
$(\varphi,N)$ where ![]() $\varphi$ is not regular semi-simple).
$\varphi$ is not regular semi-simple).
Moreover (still in the ![]() ${\rm GL}_n$ case), the conjectured functor
${\rm GL}_n$ case), the conjectured functor ![]() $R_G$ should be uniquely determined by the conditions in Conjecture 1.2 (see § 4.7 for more details). After formal completion we can prove a result in that direction. For a character
$R_G$ should be uniquely determined by the conditions in Conjecture 1.2 (see § 4.7 for more details). After formal completion we can prove a result in that direction. For a character ![]() $\chi :\mathfrak {Z}_G\rightarrow C$ we write
$\chi :\mathfrak {Z}_G\rightarrow C$ we write ![]() $\hat{\mathcal{H}}_{G,\chi }$ for the completion of the Iwahori–Hecke algebra
$\hat{\mathcal{H}}_{G,\chi }$ for the completion of the Iwahori–Hecke algebra ![]() $\mathcal {H}_G$ with respect to the kernel of
$\mathcal {H}_G$ with respect to the kernel of ![]() $\chi$. Similarly, we can consider the formal completion
$\chi$. Similarly, we can consider the formal completion ![]() $\hat X_{\check G,\chi }$ of
$\hat X_{\check G,\chi }$ of ![]() $X_{\check G}$ with respect to the pre-image of (the closed point of the adjoint quotient defined by)
$X_{\check G}$ with respect to the pre-image of (the closed point of the adjoint quotient defined by) ![]() $\chi$ in
$\chi$ in ![]() $X_{\check G}$. Then (1.1) extends to a functor
$X_{\check G}$. Then (1.1) extends to a functor
and similarly for (standard) Levi subgroups ![]() $M\subset G$.
$M\subset G$.
Theorem 1.7 Let ![]() $\varphi \in \check G(C)$ be regular semi-simple and let
$\varphi \in \check G(C)$ be regular semi-simple and let ![]() $\chi :\mathfrak {Z}_G\rightarrow C$ denote the character defined by the image of
$\chi :\mathfrak {Z}_G\rightarrow C$ denote the character defined by the image of ![]() $\varphi$ in the adjoint quotient. The set of functors
$\varphi$ in the adjoint quotient. The set of functors
for standard Levi subgroups ![]() $M\subset G$, is uniquely determined (up to isomorphism) by requiring that they are
$M\subset G$, is uniquely determined (up to isomorphism) by requiring that they are ![]() $\hat {\mathfrak {Z}}_{M,\chi }$-linear, compatible with parabolic induction, and that
$\hat {\mathfrak {Z}}_{M,\chi }$-linear, compatible with parabolic induction, and that ![]() $\hat R_{T,\chi }$ is induced by the identification
$\hat R_{T,\chi }$ is induced by the identification
Finally, I would like to mention that I was led to Conjecture 1.2 by considerations about ![]() $p$-adic automorphic forms and moduli spaces of
$p$-adic automorphic forms and moduli spaces of ![]() $p$-adic Galois representations. In fact I hope that the conjecture extends (in a yet rather vague sense) to a
$p$-adic Galois representations. In fact I hope that the conjecture extends (in a yet rather vague sense) to a ![]() $p$-adic picture, which should have implications on the computation of locally algebraic vectors in the
$p$-adic picture, which should have implications on the computation of locally algebraic vectors in the ![]() $p$-adic Langlands program, as in work of Pyvovarov [Reference PyvovarovPyv20c], which in fact inspired the computation in § 4.6. I do not pursue this direction here, but will come back to it in the future.
$p$-adic Langlands program, as in work of Pyvovarov [Reference PyvovarovPyv20c], which in fact inspired the computation in § 4.6. I do not pursue this direction here, but will come back to it in the future.
2. Spaces of L-parameters
We fix a field ![]() $C$ of characteristic zero and a prime
$C$ of characteristic zero and a prime ![]() $p$ with power
$p$ with power ![]() $q=p^r$. Let
$q=p^r$. Let ![]() $G$ be a linear algebraic group over
$G$ be a linear algebraic group over ![]() $C$ and let
$C$ and let ![]() $\mathfrak {g}$ denote its Lie algebra, considered as a
$\mathfrak {g}$ denote its Lie algebra, considered as a ![]() $C$-scheme. We define the
$C$-scheme. We define the ![]() $C$-scheme
$C$-scheme ![]() $X_G$ as the scheme representing the functor
$X_G$ as the scheme representing the functor
on the category of ![]() $C$-algebras.
$C$-algebras.
The scheme ![]() $X_G$ comes with a canonical
$X_G$ comes with a canonical ![]() $G$-action, by conjugation on
$G$-action, by conjugation on ![]() $G$ and by the adjoint action on
$G$ and by the adjoint action on ![]() $\mathfrak {g}$. We write
$\mathfrak {g}$. We write ![]() $[X_G/G]$ for the stack quotient of
$[X_G/G]$ for the stack quotient of ![]() $X_G$ by this action. For obvious reasons this is an algebraic stack (or Artin stack). Given a homomorphism
$X_G$ by this action. For obvious reasons this is an algebraic stack (or Artin stack). Given a homomorphism ![]() $\alpha :G\rightarrow H$ of linear algebraic groups, we obtain canonical morphisms
$\alpha :G\rightarrow H$ of linear algebraic groups, we obtain canonical morphisms ![]() $X_G\rightarrow X_H$ of schemes and
$X_G\rightarrow X_H$ of schemes and ![]() $[X_G/G]\rightarrow [X_H/H]$ of stacks.
$[X_G/G]\rightarrow [X_H/H]$ of stacks.
2.1 Basic properties
We study the basic properties of the spaces ![]() $X_G$ and
$X_G$ and ![]() $[X_G/G]$. Some of the results in this section were also obtained, in the more general situation of stacks of L-parameters, by Dat, Helm, Kurinczuk and Moss [Reference Dat, Helm, Kurinczuk and MossDHKM20] and Zhu [Reference ZhuZhu20].
$[X_G/G]$. Some of the results in this section were also obtained, in the more general situation of stacks of L-parameters, by Dat, Helm, Kurinczuk and Moss [Reference Dat, Helm, Kurinczuk and MossDHKM20] and Zhu [Reference ZhuZhu20].
(i) Assume that
 $G$ is reductive. Then
$G$ is reductive. Then  $X_{G}$ is a complete intersection inside
$X_{G}$ is a complete intersection inside  $G\times \mathfrak {g}$ and has dimension
$G\times \mathfrak {g}$ and has dimension  $\dim G$.
$\dim G$.(ii) If
 $G={\rm GL}_n$, then
$G={\rm GL}_n$, then  $X_G$ is reduced and the irreducible components are in bijection with the set of
$X_G$ is reduced and the irreducible components are in bijection with the set of  $G$-orbits in the nilpotent cone
$G$-orbits in the nilpotent cone  $\mathcal {N}_G\subset \mathfrak {g}$ of
$\mathcal {N}_G\subset \mathfrak {g}$ of  $G$. Moreover, let
$G$. Moreover, let  $\eta =(\varphi _\eta,N_\eta )\in X_G$ be a generic point of an irreducible component. Then
$\eta =(\varphi _\eta,N_\eta )\in X_G$ be a generic point of an irreducible component. Then  $\varphi _\eta$ is regular semi-simple.
$\varphi _\eta$ is regular semi-simple.
Proof. (ii) This is [Reference Hartl and HellmannHH20, Theorem 3.2] or [Reference HelmHel20, Proposition 4.2].
(i) Helm's argument from [Reference HelmHel20] directly generalizes to the case of a reductive group: as ![]() $X_G\subset G\times \mathfrak {g}$ is cut out by
$X_G\subset G\times \mathfrak {g}$ is cut out by ![]() $\dim G$ equations, it is enough to show that
$\dim G$ equations, it is enough to show that ![]() $X_G$ is equidimensional of dimension
$X_G$ is equidimensional of dimension ![]() $\dim G$.
$\dim G$.
Let us write ![]() $f:X_G\rightarrow \mathfrak {g}$ for the projection to the Lie algebra. We first claim that
$f:X_G\rightarrow \mathfrak {g}$ for the projection to the Lie algebra. We first claim that ![]() $f$ set-theoretically factors over the nilpotent cone
$f$ set-theoretically factors over the nilpotent cone ![]() $\mathcal {N}_G\subset \operatorname {Lie} G$. In order to do so we choose an embedding
$\mathcal {N}_G\subset \operatorname {Lie} G$. In order to do so we choose an embedding ![]() $G\hookrightarrow \operatorname {GL}_m$ for some
$G\hookrightarrow \operatorname {GL}_m$ for some ![]() $m$. Then
$m$. Then ![]() $X_G$ embeds into
$X_G$ embeds into ![]() $X_{\operatorname {GL}_m}$ and, given
$X_{\operatorname {GL}_m}$ and, given ![]() $(\varphi,N)\in X_G$ [Reference Hartl and HellmannHH20, Lemma 2.3], implies that
$(\varphi,N)\in X_G$ [Reference Hartl and HellmannHH20, Lemma 2.3], implies that ![]() $N$ is mapped to a nilpotent element of
$N$ is mapped to a nilpotent element of ![]() $\mathfrak {gl}_m$. This implies
$\mathfrak {gl}_m$. This implies ![]() $N\in \mathcal {N}_G$.
$N\in \mathcal {N}_G$.
The scheme ![]() $\mathcal {N}_G$ is irreducible and a finite union of (locally closed)
$\mathcal {N}_G$ is irreducible and a finite union of (locally closed) ![]() $G$-orbits for the adjoint action, as
$G$-orbits for the adjoint action, as ![]() $G$ is reductive. Let
$G$ is reductive. Let ![]() $Z\subset \mathcal {N}_G$ be such a
$Z\subset \mathcal {N}_G$ be such a ![]() $G$-orbit and let
$G$-orbit and let ![]() $\mathcal {G}_Z\subset G\times Z$ be the
$\mathcal {G}_Z\subset G\times Z$ be the ![]() $Z$-group scheme of centralizers of the points in
$Z$-group scheme of centralizers of the points in ![]() $Z$, that is, the fiber
$Z$, that is, the fiber ![]() $G_z$ of
$G_z$ of ![]() $\mathcal {G}_Z$ over
$\mathcal {G}_Z$ over ![]() $z\in Z$ is the centralizer of
$z\in Z$ is the centralizer of ![]() $z$ in
$z$ in ![]() $G$. Then the translation action makes
$G$. Then the translation action makes ![]() $f^{-1}(Z)$ (if non-empty) into a right
$f^{-1}(Z)$ (if non-empty) into a right ![]() $\mathcal {G}_Z$-torsor. In particular, in this case we have
$\mathcal {G}_Z$-torsor. In particular, in this case we have ![]() $\dim f^{-1}(Z)=\dim Z+\dim _Z \mathcal {G}_Z=\dim Z+\dim G_z=\dim G$, where
$\dim f^{-1}(Z)=\dim Z+\dim _Z \mathcal {G}_Z=\dim Z+\dim G_z=\dim G$, where ![]() $z\in Z$ is any (closed) point. The scheme
$z\in Z$ is any (closed) point. The scheme ![]() $X_G$ now is the union of the locally closed subsets
$X_G$ now is the union of the locally closed subsets ![]() $f^{-1}(Z)$, where
$f^{-1}(Z)$, where ![]() $Z$ runs over all the
$Z$ runs over all the ![]() $G$-orbits in
$G$-orbits in ![]() $\mathcal {N}_G$. As all these locally closed subsets (if
$\mathcal {N}_G$. As all these locally closed subsets (if ![]() $\neq \emptyset$) have dimension
$\neq \emptyset$) have dimension ![]() $\dim G$, their closures are precisely the irreducible components of
$\dim G$, their closures are precisely the irreducible components of ![]() $X_G$. It follows that
$X_G$. It follows that ![]() $X_G$ is equidimensional of dimension
$X_G$ is equidimensional of dimension ![]() $\dim G$ as claimed.
$\dim G$ as claimed.
Remark 2.2 (a) The proof implies that the irreducible components of ![]() $X_G$ are indexed by a subset of the
$X_G$ are indexed by a subset of the ![]() $G$-orbits in
$G$-orbits in ![]() $\mathcal {N}_G$. We expect that the conclusion of (ii) holds true for a general reductive group, that is, the scheme
$\mathcal {N}_G$. We expect that the conclusion of (ii) holds true for a general reductive group, that is, the scheme ![]() $X_G$ should be reduced and a complete intersection. The description of the irreducible components should be slightly more involved in general. Namely, the irreducible components should be in bijection with the
$X_G$ should be reduced and a complete intersection. The description of the irreducible components should be slightly more involved in general. Namely, the irreducible components should be in bijection with the ![]() $G$-orbits of pairs
$G$-orbits of pairs ![]() $(N,\alpha )$ consisting of an element
$(N,\alpha )$ consisting of an element ![]() $N$ in the nilpotent cone and a connected component
$N$ in the nilpotent cone and a connected component ![]() $\alpha$ of the stabilizer of
$\alpha$ of the stabilizer of ![]() $N$ (note that in the case
$N$ (note that in the case ![]() $G=\rm {SL}_2$ these stabilizers are not connected in general). Moreover, we expect that the element
$G=\rm {SL}_2$ these stabilizers are not connected in general). Moreover, we expect that the element ![]() $\varphi$ should be regular semi-simple at the generic points of the irreducible components. The first part (
$\varphi$ should be regular semi-simple at the generic points of the irreducible components. The first part (![]() $X_G$ is reduced and a complete intersection) can be deduced from [Reference Dat, Helm, Kurinczuk and MossDHKM20, Corollary 2.4 and Proposition 2.7] (compare also [Reference ZhuZhu20, Proposition 3.1.6]) after noting that
$X_G$ is reduced and a complete intersection) can be deduced from [Reference Dat, Helm, Kurinczuk and MossDHKM20, Corollary 2.4 and Proposition 2.7] (compare also [Reference ZhuZhu20, Proposition 3.1.6]) after noting that ![]() $X_G$ is a connected component of the fiber over
$X_G$ is a connected component of the fiber over ![]() $C$ of the scheme
$C$ of the scheme ![]() $\underline {Z}^1(W_F^\circ /P_F,G)$ of [Reference Dat, Helm, Kurinczuk and MossDHKM20].
$\underline {Z}^1(W_F^\circ /P_F,G)$ of [Reference Dat, Helm, Kurinczuk and MossDHKM20].
(b) The only ingredient in the proof of (i) that uses the assumption that ![]() $G$ is reductive is the fact that
$G$ is reductive is the fact that ![]() $G$ acts with only finitely many orbits on its nilpotent cone. More precisely, let
$G$ acts with only finitely many orbits on its nilpotent cone. More precisely, let ![]() $G$ be an arbitrary linear algebraic group and let
$G$ be an arbitrary linear algebraic group and let ![]() $G\hookrightarrow {\rm GL}_m$ be a faithful representation. Then the proof of (i) works if
$G\hookrightarrow {\rm GL}_m$ be a faithful representation. Then the proof of (i) works if ![]() $G$ acts with finitely many orbits on
$G$ acts with finitely many orbits on ![]() $\operatorname {Lie} G\cap \mathcal {N}_{\operatorname {GL}_m}$. This is not true in general, even if
$\operatorname {Lie} G\cap \mathcal {N}_{\operatorname {GL}_m}$. This is not true in general, even if ![]() $G$ is a parabolic subgroup in
$G$ is a parabolic subgroup in ![]() $\operatorname {GL}_m$ (see [Reference Boos and BuloisBB19]): it follows from [Reference Boos and BuloisBB19] that this fails in the case of a Borel subgroup in
$\operatorname {GL}_m$ (see [Reference Boos and BuloisBB19]): it follows from [Reference Boos and BuloisBB19] that this fails in the case of a Borel subgroup in ![]() $\operatorname {GL}_m$ for
$\operatorname {GL}_m$ for ![]() $m\geq 6$. The following example shows that the statement of the proposition also fails for Borel subgroups of
$m\geq 6$. The following example shows that the statement of the proposition also fails for Borel subgroups of ![]() ${\rm GL}_n$ for
${\rm GL}_n$ for ![]() $n\geq 9$. We have not checked that this is the optimal bound. It is very likely that
$n\geq 9$. We have not checked that this is the optimal bound. It is very likely that ![]() $X_B$ is not equidimensional if
$X_B$ is not equidimensional if ![]() $B$ is a Borel subgroup in
$B$ is a Borel subgroup in ![]() ${\rm GL}_6$.
${\rm GL}_6$.
Example 2.3 Let ![]() $r,d>0$ and
$r,d>0$ and ![]() $n=rd$. Let
$n=rd$. Let ![]() $B\subset \operatorname {GL}_n$ be the Borel subgroup of upper triangular matrices and let
$B\subset \operatorname {GL}_n$ be the Borel subgroup of upper triangular matrices and let
where each entry ![]() $q^i$ appears
$q^i$ appears ![]() $r$ times. Then a given element
$r$ times. Then a given element ![]() $N=(n_{ij})_{ij}\in {\operatorname {Lie} B}$ satisfies
$N=(n_{ij})_{ij}\in {\operatorname {Lie} B}$ satisfies ![]() $N\varphi _0=q\varphi _0 N$ if and only if
$N\varphi _0=q\varphi _0 N$ if and only if
Scaling ![]() $\varphi _0$ by multiplication with elements of the center
$\varphi _0$ by multiplication with elements of the center ![]() $Z\cong \mathbb {G}_m$, we obtain a closed embedding
$Z\cong \mathbb {G}_m$, we obtain a closed embedding ![]() $\mathbb {G}_m\times \prod _{i=1}^{d-1}\mathbb {A}^{r^2}\hookrightarrow X_B$. The
$\mathbb {G}_m\times \prod _{i=1}^{d-1}\mathbb {A}^{r^2}\hookrightarrow X_B$. The ![]() $B$-orbit of this closed subscheme is irreducible and of dimension
$B$-orbit of this closed subscheme is irreducible and of dimension
 \begin{align*} \dim \bigg(\mathbb{G}_m\times \prod_{i=1}^{d-1}\mathbb{A}^{r^2}\bigg)+ \dim B-{\rm Stab}_B(\varphi_0)&=1+\dim B+\bigg((d-1)r^2-d\frac{r(r+1)}{2}\bigg)\\ &=1+\dim B+\frac{r}{2}(dr-(2r+d)). \end{align*}
\begin{align*} \dim \bigg(\mathbb{G}_m\times \prod_{i=1}^{d-1}\mathbb{A}^{r^2}\bigg)+ \dim B-{\rm Stab}_B(\varphi_0)&=1+\dim B+\bigg((d-1)r^2-d\frac{r(r+1)}{2}\bigg)\\ &=1+\dim B+\frac{r}{2}(dr-(2r+d)). \end{align*}
In particular, we find that ![]() $X_B$ has an irreducible component of dimension strictly larger than
$X_B$ has an irreducible component of dimension strictly larger than ![]() $\dim B$ if
$\dim B$ if ![]() $dr\geq 2r+d$. On the other hand,
$dr\geq 2r+d$. On the other hand, ![]() $X_B$ always has an irreducible component of dimension
$X_B$ always has an irreducible component of dimension ![]() $\dim B$, namely
$\dim B$, namely ![]() $B\times \{0\}\subset B\times \operatorname {Lie} B$.
$B\times \{0\}\subset B\times \operatorname {Lie} B$.
Let ![]() $G$ be a reductive group and let
$G$ be a reductive group and let ![]() $P$ be a parabolic subgroup. We will write
$P$ be a parabolic subgroup. We will write ![]() $\tilde X_P$ for the scheme representing the sheafification of the functor
$\tilde X_P$ for the scheme representing the sheafification of the functor
 \begin{equation}
R\mapsto \left\{(\varphi,N,g)\in
(G\times\mathfrak{g})(R)\times G(R)/P(R)\,
\left|\,{\begin{array}{@{}c@{}} (\varphi,N)\in X_G(R) \
\text{and}\\ \varphi\in g^{-1}Pg,\\ N\in {\rm
Ad}(g^{-1})(\operatorname{Lie} P)
\end{array}}\right\}.\right.
\end{equation}
\begin{equation}
R\mapsto \left\{(\varphi,N,g)\in
(G\times\mathfrak{g})(R)\times G(R)/P(R)\,
\left|\,{\begin{array}{@{}c@{}} (\varphi,N)\in X_G(R) \
\text{and}\\ \varphi\in g^{-1}Pg,\\ N\in {\rm
Ad}(g^{-1})(\operatorname{Lie} P)
\end{array}}\right\}.\right.
\end{equation}
This is a closed ![]() $G$-invariant subscheme of
$G$-invariant subscheme of ![]() $X_G\times G/P$ (where
$X_G\times G/P$ (where ![]() $G$ acts on
$G$ acts on ![]() $G/P$ by left translation). Then
$G/P$ by left translation). Then ![]() $(\varphi,N)\mapsto (\varphi,N,1)$ induces a closed embedding
$(\varphi,N)\mapsto (\varphi,N,1)$ induces a closed embedding ![]() $X_P\hookrightarrow \tilde X_P$ which descends to an isomorphism
$X_P\hookrightarrow \tilde X_P$ which descends to an isomorphism
Moreover, the canonical projection ![]() $\tilde X_P \rightarrow X_G$ is
$\tilde X_P \rightarrow X_G$ is ![]() $G$-equivariant and the induced morphism
$G$-equivariant and the induced morphism ![]() $[\tilde X_P/G]\rightarrow [X_G/G]$ agrees under the isomorphism (2.2) with the morphism
$[\tilde X_P/G]\rightarrow [X_G/G]$ agrees under the isomorphism (2.2) with the morphism ![]() $[X_P/P]\rightarrow [X_G/G]$ induced by
$[X_P/P]\rightarrow [X_G/G]$ induced by ![]() $P\hookrightarrow G$. The following lemma is a direct consequence of this discussion.
$P\hookrightarrow G$. The following lemma is a direct consequence of this discussion.
Lemma 2.4 Let ![]() $G$ be a reductive group and
$G$ be a reductive group and ![]() $P\subset G$ be a parabolic subgroup. Then the canonical map
$P\subset G$ be a parabolic subgroup. Then the canonical map ![]() $[X_P/P]\rightarrow [X_G/G]$ induced by the inclusion
$[X_P/P]\rightarrow [X_G/G]$ induced by the inclusion ![]() $P\hookrightarrow G$ is proper.
$P\hookrightarrow G$ is proper.
We continue to assume that ![]() $G$ is reductive. We say that a point
$G$ is reductive. We say that a point ![]() $(\varphi,N)\in G\times \mathfrak {g}$ is regular, if there are only finitely many Borel subgroups
$(\varphi,N)\in G\times \mathfrak {g}$ is regular, if there are only finitely many Borel subgroups ![]() $B'\subset G$ such that
$B'\subset G$ such that ![]() $\varphi \in B'$ and
$\varphi \in B'$ and ![]() $N\in \operatorname {Lie} B'$, that is, if (for one fixed choice of a Borel
$N\in \operatorname {Lie} B'$, that is, if (for one fixed choice of a Borel ![]() $B$) the point
$B$) the point ![]() $(\varphi,N)$ has only finitely many pre-images under
$(\varphi,N)$ has only finitely many pre-images under
As this morphism is proper and the fiber dimension is upper semi-continuous on the source, the regular elements form a Zariski open subset ![]() $(G\times \mathfrak {g})^{\rm reg}\subset G\times \mathfrak {g}$. Similarly, we can define a Zariski open subset
$(G\times \mathfrak {g})^{\rm reg}\subset G\times \mathfrak {g}$. Similarly, we can define a Zariski open subset
If ![]() $P\subset G$ is a parabolic subgroup, we write
$P\subset G$ is a parabolic subgroup, we write
and ![]() $X_P^{\rm reg}=X_P\cap X_G^{\rm reg}$. Moreover, we write
$X_P^{\rm reg}=X_P\cap X_G^{\rm reg}$. Moreover, we write ![]() $\tilde X_P^{\rm reg}$ for the pre-image of
$\tilde X_P^{\rm reg}$ for the pre-image of ![]() $X_G^{\rm reg}$ under
$X_G^{\rm reg}$ under ![]() $\tilde X_P\rightarrow X_G$. Then
$\tilde X_P\rightarrow X_G$. Then ![]() $[X_P^{\rm reg}/P]=[\tilde X_P^{\rm reg}/G]$ as stacks and the morphism
$[X_P^{\rm reg}/P]=[\tilde X_P^{\rm reg}/G]$ as stacks and the morphism ![]() $\tilde X_P^{\rm reg}\rightarrow X_G^{\rm reg}$ is by construction a finite morphism. Moreover, if we write
$\tilde X_P^{\rm reg}\rightarrow X_G^{\rm reg}$ is by construction a finite morphism. Moreover, if we write ![]() $M$ for the Levi quotient of
$M$ for the Levi quotient of ![]() $P$, it is a direct consequence of the definition that the canonical projection
$P$, it is a direct consequence of the definition that the canonical projection ![]() $[X_P/P]\rightarrow [X_M/M]$ restricts to
$[X_P/P]\rightarrow [X_M/M]$ restricts to ![]() $[X_P^{\rm reg}/P]\rightarrow [X_M^{\rm reg}/M]$.
$[X_P^{\rm reg}/P]\rightarrow [X_M^{\rm reg}/M]$.
Lemma 2.5 The scheme ![]() $X_P^{\rm reg}$ is equidimensional of dimension
$X_P^{\rm reg}$ is equidimensional of dimension ![]() $\dim P$ and a complete intersection inside
$\dim P$ and a complete intersection inside ![]() $(P\times \operatorname {Lie} P)^{\rm reg}$. Moreover, the map
$(P\times \operatorname {Lie} P)^{\rm reg}$. Moreover, the map ![]() $\tilde X_P^{\rm reg}\rightarrow X_G^{\rm reg}$ is surjective and each irreducible component of
$\tilde X_P^{\rm reg}\rightarrow X_G^{\rm reg}$ is surjective and each irreducible component of ![]() $\tilde X_P^{\rm reg}$ dominates an irreducible component of
$\tilde X_P^{\rm reg}$ dominates an irreducible component of ![]() $X_G^{\rm reg}$.
$X_G^{\rm reg}$.
Proof. Following the opening lines of the proof of Proposition 2.1, the first claim follows if we show that every irreducible component of ![]() $X_P^{\rm reg}$ has dimension at most
$X_P^{\rm reg}$ has dimension at most ![]() $\dim P$. Equivalently, we can show that every irreducible component of
$\dim P$. Equivalently, we can show that every irreducible component of ![]() $\tilde X_P^{\rm reg}$ has dimension at most
$\tilde X_P^{\rm reg}$ has dimension at most ![]() $\dim G$. This is a direct consequence of the fact that
$\dim G$. This is a direct consequence of the fact that ![]() $\tilde X_P^{\rm reg}\rightarrow X_G^{\rm reg}$ is finite. It follows that every irreducible component of
$\tilde X_P^{\rm reg}\rightarrow X_G^{\rm reg}$ is finite. It follows that every irreducible component of ![]() $\tilde X_P^{\rm reg}$ has dimension equal to
$\tilde X_P^{\rm reg}$ has dimension equal to ![]() $\dim G$. As
$\dim G$. As ![]() $\tilde X_P^{\rm reg}\rightarrow X_G^{\rm reg}$ is finite and
$\tilde X_P^{\rm reg}\rightarrow X_G^{\rm reg}$ is finite and ![]() $X_G$ is equidimensional of dimension
$X_G$ is equidimensional of dimension ![]() $\dim G$ it follows that every irreducible component of
$\dim G$ it follows that every irreducible component of ![]() $\tilde X_P^{\rm reg}$ dominates an irreducible component of
$\tilde X_P^{\rm reg}$ dominates an irreducible component of ![]() $X_G^{\rm reg}$.
$X_G^{\rm reg}$.
It remains to show that ![]() $\tilde X_P^{\rm reg}\rightarrow X_G^{\rm reg}$ is surjective. In fact we even show that
$\tilde X_P^{\rm reg}\rightarrow X_G^{\rm reg}$ is surjective. In fact we even show that ![]() $\tilde X_P\rightarrow X_G$ is surjective. We easily reduce to the case
$\tilde X_P\rightarrow X_G$ is surjective. We easily reduce to the case ![]() $P=B$ a Borel subgroup, and, choosing an embedding
$P=B$ a Borel subgroup, and, choosing an embedding ![]() $G\hookrightarrow \operatorname {GL}_n$, we can reduce to the case of
$G\hookrightarrow \operatorname {GL}_n$, we can reduce to the case of ![]() $\operatorname {GL}_n$. There we can check the claim on
$\operatorname {GL}_n$. There we can check the claim on ![]() $k$-valued points for algebraically closed fields
$k$-valued points for algebraically closed fields ![]() $k$, where it easily follows by looking at the Jordan canonical forms of
$k$, where it easily follows by looking at the Jordan canonical forms of ![]() $\varphi$ and
$\varphi$ and ![]() $N$.
$N$.
Remark 2.6 We remark that ![]() $X_P^{\rm reg}\subset X_P$ is open, but not dense in general, as can be deduced from Lemma 2.5 and Example 2.3. If
$X_P^{\rm reg}\subset X_P$ is open, but not dense in general, as can be deduced from Lemma 2.5 and Example 2.3. If ![]() $G$ is reductive then we expect that
$G$ is reductive then we expect that ![]() $X_G^{\rm reg}$ is dense in
$X_G^{\rm reg}$ is dense in ![]() $X_G$. In the case of
$X_G$. In the case of ![]() $\operatorname {GL}_n$ this is a consequence of Proposition 2.1.
$\operatorname {GL}_n$ this is a consequence of Proposition 2.1.
If ![]() $G=\operatorname {GL}_n$ and
$G=\operatorname {GL}_n$ and ![]() $P\subset G$ is a parabolic subgroup, then
$P\subset G$ is a parabolic subgroup, then ![]() $G/P$ can be identified with the variety of flags of type
$G/P$ can be identified with the variety of flags of type ![]() $P$. In particular, we can identify
$P$. In particular, we can identify ![]() $\tilde X_P$ with the variety of triples
$\tilde X_P$ with the variety of triples ![]() $(\varphi,N,\mathcal {F})$ consisting of
$(\varphi,N,\mathcal {F})$ consisting of ![]() $(\varphi,N)\in X_G$ and a
$(\varphi,N)\in X_G$ and a ![]() $(\varphi,N)$-stable flag of type
$(\varphi,N)$-stable flag of type ![]() $P$. From now on we will often use this identification.
$P$. From now on we will often use this identification.
Lemma 2.7 Let ![]() $G={\rm GL}_n$ and let
$G={\rm GL}_n$ and let ![]() $P\subset G$ be a parabolic. Then
$P\subset G$ be a parabolic. Then ![]() $\tilde X_P^{\rm reg}$ is reduced.
$\tilde X_P^{\rm reg}$ is reduced.
Proof. To prove that ![]() $\tilde X_P^{\rm reg}$ is reduced, it remains to show that it is generically reduced. Let
$\tilde X_P^{\rm reg}$ is reduced, it remains to show that it is generically reduced. Let ![]() $\xi =(\varphi _\xi,N_\xi,\mathcal {F}_\xi )\in \tilde X_P^{\rm reg}$ be a generic point. Under
$\xi =(\varphi _\xi,N_\xi,\mathcal {F}_\xi )\in \tilde X_P^{\rm reg}$ be a generic point. Under ![]() $\tilde \beta _P:\tilde X_P^{\rm reg}\rightarrow X_G$ the point
$\tilde \beta _P:\tilde X_P^{\rm reg}\rightarrow X_G$ the point ![]() $\xi$ maps to a generic point
$\xi$ maps to a generic point ![]() $\eta =(\varphi _\xi,N_\xi )$ of
$\eta =(\varphi _\xi,N_\xi )$ of ![]() $X_G$ and hence
$X_G$ and hence ![]() $\varphi _\xi$ is regular semi-simple. It is enough to show that
$\varphi _\xi$ is regular semi-simple. It is enough to show that ![]() $\tilde \beta _P^{-1}(\eta )$ is reduced. But as
$\tilde \beta _P^{-1}(\eta )$ is reduced. But as ![]() $\varphi _\xi$ is regular semi-simple the space of
$\varphi _\xi$ is regular semi-simple the space of ![]() $\varphi _\xi$-stable flags is a finite disjoint union of reduced points. Hence, its closed subspace of flags that are in addition stable under
$\varphi _\xi$-stable flags is a finite disjoint union of reduced points. Hence, its closed subspace of flags that are in addition stable under ![]() $N_\xi$ has to be reduced as well.
$N_\xi$ has to be reduced as well.
Remark 2.8 Let ![]() $n\leq 5$ and
$n\leq 5$ and ![]() $P\subset \operatorname {GL}_n$ a parabolic subgroup. We point out that the argument in Remark 2.2(b) implies that
$P\subset \operatorname {GL}_n$ a parabolic subgroup. We point out that the argument in Remark 2.2(b) implies that ![]() $X_P$ is a complete intersection in
$X_P$ is a complete intersection in ![]() $P\times \operatorname {Lie} P$. But if
$P\times \operatorname {Lie} P$. But if ![]() $n\geq 4$, it is not true that every irreducible component of
$n\geq 4$, it is not true that every irreducible component of ![]() $\tilde X_P$ dominates an irreducible component of
$\tilde X_P$ dominates an irreducible component of ![]() $X_{\operatorname {GL}_n}$. Indeed, one can compute that if
$X_{\operatorname {GL}_n}$. Indeed, one can compute that if ![]() $n=4$ and
$n=4$ and ![]() $P=B$ is a Borel, then there is an irreducible component of
$P=B$ is a Borel, then there is an irreducible component of ![]() $\tilde X_B$ on which the Frobenius
$\tilde X_B$ on which the Frobenius ![]() $\varphi$ is semi-simple with eigenvalues
$\varphi$ is semi-simple with eigenvalues ![]() $\lambda,q\lambda,q\lambda,q^2\lambda$ for some indeterminate
$\lambda,q\lambda,q\lambda,q^2\lambda$ for some indeterminate ![]() $\lambda$. This component clearly cannot dominate an irreducible component of
$\lambda$. This component clearly cannot dominate an irreducible component of ![]() $X_{\operatorname {GL}_4}$. However, for
$X_{\operatorname {GL}_4}$. However, for ![]() $n\leq 3$ one can compute that every irreducible component of
$n\leq 3$ one can compute that every irreducible component of ![]() $X_P$ is the closure of an irreducible component of
$X_P$ is the closure of an irreducible component of ![]() $X_P^{\rm reg}$. In particular, we deduce that
$X_P^{\rm reg}$. In particular, we deduce that ![]() $X_P$ is reduced if
$X_P$ is reduced if ![]() $n\leq 3$. In the general case (
$n\leq 3$. In the general case (![]() $P\subset G$ a parabolic subgroup of a reductive group) we do not know whether
$P\subset G$ a parabolic subgroup of a reductive group) we do not know whether ![]() $X_P$ is reduced.
$X_P$ is reduced.
Lemma 2.9 Let ![]() $G$ be reductive and
$G$ be reductive and ![]() $P\subset G$ be parabolic with Levi quotient
$P\subset G$ be parabolic with Levi quotient ![]() $M$.
$M$.
(i) The morphism
 $X_P^{\rm reg}\rightarrow X_M^{\rm reg}$ has finite Tor dimension.
$X_P^{\rm reg}\rightarrow X_M^{\rm reg}$ has finite Tor dimension.(ii) Let
 $P'\subset P$ be a second parabolic subgroup. Let
$P'\subset P$ be a second parabolic subgroup. Let  $M'$ denote the Levi quotient of
$M'$ denote the Levi quotient of  $P'$ and
$P'$ and  $P'_{M}\subset M$ denote the image of
$P'_{M}\subset M$ denote the image of  $P'$ in
$P'$ in  $M$. Then the diagrams
(2.3)are cartesian and the fiber product on the right-hand side is Tor-independent.
$M$. Then the diagrams
(2.3)are cartesian and the fiber product on the right-hand side is Tor-independent.
Proof. (i) Let ![]() $U\subset P$ denote the unipotent radical of
$U\subset P$ denote the unipotent radical of ![]() $P$ and fix a section
$P$ and fix a section ![]() $M\hookrightarrow P$ of the canonical projection. We write
$M\hookrightarrow P$ of the canonical projection. We write ![]() $\mathfrak {u}\subset \mathfrak {p}$ for the Lie algebras of
$\mathfrak {u}\subset \mathfrak {p}$ for the Lie algebras of ![]() $U$ and
$U$ and ![]() $P$ and
$P$ and ![]() $\mathfrak {m}$ for the Lie algebra of
$\mathfrak {m}$ for the Lie algebra of ![]() $M$. Then we obtain a commutative diagram
$M$. Then we obtain a commutative diagram

where the horizontal arrow ![]() $\psi$ is induced by multiplication and the other two morphisms are the canonical projections. Let
$\psi$ is induced by multiplication and the other two morphisms are the canonical projections. Let ![]() $r=\dim M$ and
$r=\dim M$ and ![]() $s=\dim U$. Let
$s=\dim U$. Let ![]() $I\subset \Gamma (P\times \operatorname {Lie} P,\mathcal {O}_{P\times \operatorname {Lie} P})$ be the ideal defining
$I\subset \Gamma (P\times \operatorname {Lie} P,\mathcal {O}_{P\times \operatorname {Lie} P})$ be the ideal defining ![]() $X_P\hookrightarrow P\times \operatorname {Lie} P$, that is, the ideal generated by the entries of the matrix
$X_P\hookrightarrow P\times \operatorname {Lie} P$, that is, the ideal generated by the entries of the matrix ![]() ${\rm Ad}(\varphi )(N)-q^{-1}N$, where
${\rm Ad}(\varphi )(N)-q^{-1}N$, where ![]() $\varphi$ and
$\varphi$ and ![]() $N$ are the universal elements over
$N$ are the universal elements over ![]() $P$ and
$P$ and ![]() $\operatorname {Lie} P$. Then we deduce from the diagram that
$\operatorname {Lie} P$. Then we deduce from the diagram that ![]() $I$ can be generated by elements
$I$ can be generated by elements ![]() $f_1,\ldots, f_r,g_1\ldots,g_s$ such that
$f_1,\ldots, f_r,g_1\ldots,g_s$ such that
where ![]() $(f_1,\ldots,f_r)$ is the ideal defining
$(f_1,\ldots,f_r)$ is the ideal defining ![]() $X_M\subset M\times \mathfrak {m}$. It follows that the ideal
$X_M\subset M\times \mathfrak {m}$. It follows that the ideal ![]() $(g_1,\ldots, g_s)$ is the ideal defining
$(g_1,\ldots, g_s)$ is the ideal defining ![]() $X_P$ as a closed subscheme of
$X_P$ as a closed subscheme of ![]() $\pi ^{-1}(X_M)\cong \mathbb {A}^{2s}_{X_M}$.
$\pi ^{-1}(X_M)\cong \mathbb {A}^{2s}_{X_M}$.
Let us now write ![]() $K(g_1,\ldots, g_s)$ for the Koszul complex defined by
$K(g_1,\ldots, g_s)$ for the Koszul complex defined by ![]() $g_1,\ldots, g_s$ on the open subscheme
$g_1,\ldots, g_s$ on the open subscheme ![]() $\pi ^{-1}(X_M)^{\rm reg}=\pi ^{-1}(X_M)\cap (P\times \operatorname {Lie} P)^{\rm reg}$ of
$\pi ^{-1}(X_M)^{\rm reg}=\pi ^{-1}(X_M)\cap (P\times \operatorname {Lie} P)^{\rm reg}$ of ![]() $\pi ^{-1}(X_M)$. This is a finite complex of flat
$\pi ^{-1}(X_M)$. This is a finite complex of flat ![]() $\mathcal {O}_{X_M}$-modules and we claim that it is a resolution of
$\mathcal {O}_{X_M}$-modules and we claim that it is a resolution of ![]() $\mathcal {O}_{X_P^{\rm reg}}$. Indeed,
$\mathcal {O}_{X_P^{\rm reg}}$. Indeed, ![]() $g_1,\ldots,g_s$ cut out the closed subscheme
$g_1,\ldots,g_s$ cut out the closed subscheme ![]() $X_P^{\rm reg}\subset \pi ^{-1}(X_M)^{\rm reg}$ which is of codimension
$X_P^{\rm reg}\subset \pi ^{-1}(X_M)^{\rm reg}$ which is of codimension ![]() $s$ by Lemma 2.5. As
$s$ by Lemma 2.5. As ![]() $\pi ^{-1}(X_M)^{\rm reg}$ is Cohen–Macaulay (it is an open subscheme of an affine space over
$\pi ^{-1}(X_M)^{\rm reg}$ is Cohen–Macaulay (it is an open subscheme of an affine space over ![]() $X_M$ and
$X_M$ and ![]() $X_M$ is Cohen–Macaulay as a consequence of Proposition 2.1) it follows from [Reference Grothendieck and DieudonnéEGAIV.1, Corollaire 16.5.6] that
$X_M$ is Cohen–Macaulay as a consequence of Proposition 2.1) it follows from [Reference Grothendieck and DieudonnéEGAIV.1, Corollaire 16.5.6] that ![]() $g_1\ldots,g_s$ is a regular sequence and hence the Koszul complex is a resolution of its zeroth cohomology which is
$g_1\ldots,g_s$ is a regular sequence and hence the Koszul complex is a resolution of its zeroth cohomology which is ![]() $\mathcal {O}_{X_P^{\rm reg}}$.
$\mathcal {O}_{X_P^{\rm reg}}$.
(ii) The fact that the squares are fiber products follows from the fact that ![]() $P'$ is the pre-image of
$P'$ is the pre-image of ![]() $P'_M$ under
$P'_M$ under ![]() $P\rightarrow M$. We show that the square on the right is Tor-independent. As in (i) we have a Koszul complex
$P\rightarrow M$. We show that the square on the right is Tor-independent. As in (i) we have a Koszul complex ![]() $K(g_1,\ldots, g_s)$ on
$K(g_1,\ldots, g_s)$ on ![]() $\pi ^{-1}(X_M)^{\rm reg}$ which is a
$\pi ^{-1}(X_M)^{\rm reg}$ which is a ![]() $\mathcal {O}_{X^{\rm reg}_M}$-flat resolution of
$\mathcal {O}_{X^{\rm reg}_M}$-flat resolution of ![]() $\mathcal {O}_{X_P^{\rm reg}}$. Consider the closed embedding
$\mathcal {O}_{X_P^{\rm reg}}$. Consider the closed embedding
As (2.3) is cartesian, the restrictions of ![]() $g_1,\ldots, g_s$ to
$g_1,\ldots, g_s$ to ![]() $\pi ^{-1}(X_{P'_M})\cap (P\times \operatorname {Lie} P)^{\rm reg}$ generate the ideal defining the closed embedding (2.4), and it remains to show that the pullback of the Koszul complex
$\pi ^{-1}(X_{P'_M})\cap (P\times \operatorname {Lie} P)^{\rm reg}$ generate the ideal defining the closed embedding (2.4), and it remains to show that the pullback of the Koszul complex ![]() $K(g_1,\ldots, g_s)$ along (2.4) is a resolution of its zeroth cohomology group; that is, we need to show that
$K(g_1,\ldots, g_s)$ along (2.4) is a resolution of its zeroth cohomology group; that is, we need to show that ![]() $g_1,\ldots, g_s$ is a regular sequence in
$g_1,\ldots, g_s$ is a regular sequence in
Now
is an open subscheme and hence it is Cohen–Macaulay as ![]() $X_{P'_M}^{\rm reg}$ is Cohen–Macaulay by Lemma 2.5. The claim now follows again from [Reference Grothendieck and DieudonnéEGAIV.1, Corollaire 16.5.6] and the fact that
$X_{P'_M}^{\rm reg}$ is Cohen–Macaulay by Lemma 2.5. The claim now follows again from [Reference Grothendieck and DieudonnéEGAIV.1, Corollaire 16.5.6] and the fact that ![]() $X_{P'}^{\rm reg}$ is equidimensional of dimension
$X_{P'}^{\rm reg}$ is equidimensional of dimension ![]() $\dim \pi ^{-1}(X_{P'_M}^{\rm reg})-s$.
$\dim \pi ^{-1}(X_{P'_M}^{\rm reg})-s$.
Example 2.10 Let us point out that the left cartesian diagram of (2.3) is not necessarily Tor-independent without restricting to the regular locus. Let us consider ![]() $r=d=3$ (so that
$r=d=3$ (so that ![]() $dr=2r+d$) in Example 2.3. Let
$dr=2r+d$) in Example 2.3. Let ![]() $B\subset \operatorname {GL}_n$ be the Borel subgroup of upper triangular matrices, where
$B\subset \operatorname {GL}_n$ be the Borel subgroup of upper triangular matrices, where ![]() $n=rd=9$. Then the above example shows that
$n=rd=9$. Then the above example shows that ![]() $X_B$ is not equidimensional, and hence the defining ideal is not generated by a regular sequence. Let
$X_B$ is not equidimensional, and hence the defining ideal is not generated by a regular sequence. Let ![]() $P\subset \operatorname {GL}_9$ be a standard parabolic containing
$P\subset \operatorname {GL}_9$ be a standard parabolic containing ![]() $B$ with Levi
$B$ with Levi ![]() $M=\operatorname {GL}_5\times \operatorname {GL}_4$. Then the classification of [Reference Boos and BuloisBB19] shows that
$M=\operatorname {GL}_5\times \operatorname {GL}_4$. Then the classification of [Reference Boos and BuloisBB19] shows that ![]() $P$ as well as the Borel
$P$ as well as the Borel ![]() $B_M$ of
$B_M$ of ![]() $M$ have the property that they act only via finitely many orbits on
$M$ have the property that they act only via finitely many orbits on ![]() $\operatorname {Lie} P\cap \mathcal {N}_{\operatorname {GL}_9}$ or
$\operatorname {Lie} P\cap \mathcal {N}_{\operatorname {GL}_9}$ or ![]() $\operatorname {Lie} B_M\cap \mathcal {N}_{M}$. In particular,
$\operatorname {Lie} B_M\cap \mathcal {N}_{M}$. In particular, ![]() $X_P$ and
$X_P$ and ![]() $X_{B_M}$ are complete intersections in
$X_{B_M}$ are complete intersections in ![]() $P\times \operatorname {Lie} P$ or
$P\times \operatorname {Lie} P$ or ![]() $B_M\times \operatorname {Lie} B_M$ by Remark 2.2. As in the proof above, we can construct generators
$B_M\times \operatorname {Lie} B_M$ by Remark 2.2. As in the proof above, we can construct generators ![]() $f_1,\ldots, f_{\dim B}$ of the ideal defining
$f_1,\ldots, f_{\dim B}$ of the ideal defining ![]() $X_B\subset B\times \operatorname {Lie} B$ such that Tor-independence of (2.3) is equivalent to exactness of the Koszul complex
$X_B\subset B\times \operatorname {Lie} B$ such that Tor-independence of (2.3) is equivalent to exactness of the Koszul complex ![]() $K(f_1,\ldots, f_{\dim B})$ in negative degrees. Let
$K(f_1,\ldots, f_{\dim B})$ in negative degrees. Let ![]() $x\in X_B\subset B\times \operatorname {Lie} B$ be a point that lies on an irreducible component of
$x\in X_B\subset B\times \operatorname {Lie} B$ be a point that lies on an irreducible component of ![]() $X_B$ of dimension strictly larger than
$X_B$ of dimension strictly larger than ![]() $\dim B$. Then (the germs of)
$\dim B$. Then (the germs of) ![]() $f_1,\ldots, f_{\dim B}$ lie in the maximal ideal
$f_1,\ldots, f_{\dim B}$ lie in the maximal ideal ![]() $\mathfrak {m}_{B\times \operatorname {Lie} B,x}\subset \mathcal {O}_{B\times \operatorname {Lie} B,x}$ and the Koszul complex defined by these elements is not exact, as they do not form a regular sequence (because
$\mathfrak {m}_{B\times \operatorname {Lie} B,x}\subset \mathcal {O}_{B\times \operatorname {Lie} B,x}$ and the Koszul complex defined by these elements is not exact, as they do not form a regular sequence (because ![]() $\mathcal {O}_{X_B,x}$ is not equidimensional of dimension
$\mathcal {O}_{X_B,x}$ is not equidimensional of dimension ![]() $\dim B$).
$\dim B$).
We reformulate the first claim of the lemma in terms of stacks.
Corollary 2.11 Let ![]() $P'\subset P\subset G$ be parabolic subgroups of
$P'\subset P\subset G$ be parabolic subgroups of ![]() $G$ and let
$G$ and let ![]() $M$ be the Levi quotient of
$M$ be the Levi quotient of ![]() $P$ and
$P$ and ![]() $P'_M$ the image of
$P'_M$ the image of ![]() $P'$ in M. Then the diagram
$P'$ in M. Then the diagram

of stacks is cartesian.
Proof. Note that ![]() $P\rightarrow M$ induces an isomorphism
$P\rightarrow M$ induces an isomorphism ![]() $P/P'\cong M/P'_M$. As in (2.1), we define a closed
$P/P'\cong M/P'_M$. As in (2.1), we define a closed ![]() $M$-invariant subscheme
$M$-invariant subscheme ![]() $Y_{P'_M}\subset X_M\times M/P'_M$ as the scheme representing the sheafification of the functor
$Y_{P'_M}\subset X_M\times M/P'_M$ as the scheme representing the sheafification of the functor
Then we have a canonical isomorphism ![]() $[X_{P'_M}/P'_M]\cong [Y_{P'_M}/M]$. Similarly, we define a
$[X_{P'_M}/P'_M]\cong [Y_{P'_M}/M]$. Similarly, we define a ![]() $P$-invariant closed subscheme
$P$-invariant closed subscheme ![]() $Y_{P'}\subset X_{P'}\times P/P'$ such that
$Y_{P'}\subset X_{P'}\times P/P'$ such that ![]() $[X_{P'}/P']\cong [Y_{P'}/P]$. Then the diagram
$[X_{P'}/P']\cong [Y_{P'}/P]$. Then the diagram

is cartesian by the above lemma. Let ![]() $U\subset P$ denote the unipotent radical of
$U\subset P$ denote the unipotent radical of ![]() $P$, then it follows that
$P$, then it follows that

is cartesian diagram of stacks with ![]() $M$-action and with
$M$-action and with ![]() $M$-equivariant morphisms. The claim follows by taking the quotient by the
$M$-equivariant morphisms. The claim follows by taking the quotient by the ![]() $M$-action everywhere.
$M$-action everywhere.
The objects introduced above have variants in the world of derived (or dg) schemes (see, for example, [Reference Drinfeld and GaitsgoryDG13, 0.6.8] and the references cited therein). The category of dg-schemes over ![]() $C$ canonically contains the category of
$C$ canonically contains the category of ![]() $C$-schemes as a subcategory. For any linear algebraic group
$C$-schemes as a subcategory. For any linear algebraic group ![]() $G$ we write
$G$ we write ![]() $\gamma _G:G\times \operatorname {Lie} G\rightarrow \operatorname {Lie} G$ for the morphism
$\gamma _G:G\times \operatorname {Lie} G\rightarrow \operatorname {Lie} G$ for the morphism ![]() $(\varphi,N)\mapsto {\rm Ad}(\varphi )(N)-q^{-1}N$. We denote by
$(\varphi,N)\mapsto {\rm Ad}(\varphi )(N)-q^{-1}N$. We denote by ![]() $\mathbf {X}_G$ the fiber product
$\mathbf {X}_G$ the fiber product

in the category of dg-schemes. This yields a dg-scheme ![]() $\mathbf {X}_G$ with underlying classical scheme
$\mathbf {X}_G$ with underlying classical scheme ![]() ${}^{\rm cl}\mathbf {X}_G=X_G$. If
${}^{\rm cl}\mathbf {X}_G=X_G$. If ![]() $G$ is reductive then Proposition 2.1 implies that
$G$ is reductive then Proposition 2.1 implies that ![]() $\mathbf {X}_G=X_G$. Similarly, if
$\mathbf {X}_G=X_G$. Similarly, if ![]() $P\subset G$ is a parabolic subgroup of a reductive group, we denote by
$P\subset G$ is a parabolic subgroup of a reductive group, we denote by ![]() $\mathbf {X}_P^{\rm reg}\subset \mathbf {X}_P$ the open sub-dg-scheme with underlying topological space
$\mathbf {X}_P^{\rm reg}\subset \mathbf {X}_P$ the open sub-dg-scheme with underlying topological space ![]() $X_P^{\rm reg}$. Then Lemma 2.5 implies that
$X_P^{\rm reg}$. Then Lemma 2.5 implies that ![]() $\mathbf {X}_P^{\rm reg}=X_P^{\rm reg}$ is a classical scheme.
$\mathbf {X}_P^{\rm reg}=X_P^{\rm reg}$ is a classical scheme.
For any linear algebraic group ![]() $G$ we write
$G$ we write ![]() $[\mathbf {X}_G/G]$ for the stack quotient of
$[\mathbf {X}_G/G]$ for the stack quotient of ![]() $\mathbf {X}_G$ by the canonical action of
$\mathbf {X}_G$ by the canonical action of ![]() $G$. This is an algebraic dg-stackFootnote 2 in the sense of [Reference Drinfeld and GaitsgoryDG13, 1.1]. Similarly to the case of schemes, we can view any algebraic stack as an algebraic dg-stack. Moreover, recall that every dg-stack
$G$. This is an algebraic dg-stackFootnote 2 in the sense of [Reference Drinfeld and GaitsgoryDG13, 1.1]. Similarly to the case of schemes, we can view any algebraic stack as an algebraic dg-stack. Moreover, recall that every dg-stack ![]() $S$ has an underlying classical stack
$S$ has an underlying classical stack ![]() ${}^{\rm cl}S$.
${}^{\rm cl}S$.
If ![]() $G$ is reductive and
$G$ is reductive and ![]() $P\subset G$ is a parabolic we also consider the stacks
$P\subset G$ is a parabolic we also consider the stacks ![]() $[\mathbf {X}_G^{\rm reg}/G]$ and
$[\mathbf {X}_G^{\rm reg}/G]$ and ![]() $[\mathbf {X}_P^{\rm reg}/P]$. Then
$[\mathbf {X}_P^{\rm reg}/P]$. Then
 \begin{align*} [\mathbf{X}_G/G]&=[X_G/G],\\ [\mathbf{X}_G^{\rm reg}/G]&=[X_G^{\rm reg}/G], \\ [\mathbf{X}_P^{\rm reg}/P]&=[X_P^{\rm reg}/P]. \end{align*}
\begin{align*} [\mathbf{X}_G/G]&=[X_G/G],\\ [\mathbf{X}_G^{\rm reg}/G]&=[X_G^{\rm reg}/G], \\ [\mathbf{X}_P^{\rm reg}/P]&=[X_P^{\rm reg}/P]. \end{align*}
We recall that a morphism ![]() $\mathbf {Y}_1\rightarrow \mathbf {Y}_2$ of dg-stacks is schematic if for all affine dg-schemes
$\mathbf {Y}_1\rightarrow \mathbf {Y}_2$ of dg-stacks is schematic if for all affine dg-schemes ![]() $\mathbf {Z}$ and all morphisms
$\mathbf {Z}$ and all morphisms ![]() $\mathbf {Z}\rightarrow \mathbf {Y}_2$ the fiber product
$\mathbf {Z}\rightarrow \mathbf {Y}_2$ the fiber product ![]() $\mathbf {Z}\times _{\mathbf {Y}_2}\mathbf {Y}_1$ is a dg-scheme (see [Reference Drinfeld and GaitsgoryDG13, 1.1.2]). A morphism of dg-schemes is called proper if the induced morphism of the underlying classical schemes is proper, and a morphism of algebraic dg-stacks is proper if the morphism of underlying classical stacks is proper in the sense of [Reference Laumon and Moret-BaillyLM00, Definition 7.11]. Similarly to the non-derived results above, we obtain the following lemma.
$\mathbf {Z}\times _{\mathbf {Y}_2}\mathbf {Y}_1$ is a dg-scheme (see [Reference Drinfeld and GaitsgoryDG13, 1.1.2]). A morphism of dg-schemes is called proper if the induced morphism of the underlying classical schemes is proper, and a morphism of algebraic dg-stacks is proper if the morphism of underlying classical stacks is proper in the sense of [Reference Laumon and Moret-BaillyLM00, Definition 7.11]. Similarly to the non-derived results above, we obtain the following lemma.
Lemma 2.12 Let ![]() $G$ be a reductive group and let
$G$ be a reductive group and let ![]() $P\subset G$ be a parabolic subgroup with Levi quotient
$P\subset G$ be a parabolic subgroup with Levi quotient ![]() $M$.
$M$.
(i) The morphism
 $[\mathbf {X}_P/P]\rightarrow [\mathbf {X}_G/G]$ is schematic and proper.
$[\mathbf {X}_P/P]\rightarrow [\mathbf {X}_G/G]$ is schematic and proper.(ii) Let
 $P'\subset P$ be a second parabolic subgroup and write
$P'\subset P$ be a second parabolic subgroup and write  $P'_M\subset M$ for the image of
$P'_M\subset M$ for the image of  $P'$ in
$P'$ in  $M$. Then
$M$. Then
 \[ \mathbf{X}_{P'}\cong \mathbf{X}_{P'_M}\times_{\mathbf{X}_M}\mathbf{X}_P\quad \text{and}\quad [\mathbf{X}_{P'}/P']\cong [\mathbf{X}_{P'_M}/P'_M]\times_{[\mathbf{X}_M/M]}[\mathbf{X}_P/P]. \]
\[ \mathbf{X}_{P'}\cong \mathbf{X}_{P'_M}\times_{\mathbf{X}_M}\mathbf{X}_P\quad \text{and}\quad [\mathbf{X}_{P'}/P']\cong [\mathbf{X}_{P'_M}/P'_M]\times_{[\mathbf{X}_M/M]}[\mathbf{X}_P/P]. \]
Proof. (i) As in the non-derived case we can rewrite ![]() $[\mathbf {X}_P/P]$ as
$[\mathbf {X}_P/P]$ as ![]() $[\tilde {\mathbf {X}}_P/G]$, where
$[\tilde {\mathbf {X}}_P/G]$, where ![]() $\tilde {\mathbf {X}}_P\subset \mathbf {X}_G\times G/P$ is the closed
$\tilde {\mathbf {X}}_P\subset \mathbf {X}_G\times G/P$ is the closed ![]() $G$-invariant sub-dg-scheme obtained by making
$G$-invariant sub-dg-scheme obtained by making
invariant under the ![]() $G$-action. More precisely, we can describe this dg-scheme as follows. Let us write
$G$-action. More precisely, we can describe this dg-scheme as follows. Let us write ![]() $Z\subset G\times \operatorname {Lie} G\times G/P$ for scheme representing (the sheafification of) the functor
$Z\subset G\times \operatorname {Lie} G\times G/P$ for scheme representing (the sheafification of) the functor
on ![]() $C$-algebras. By definition there is an isomorphism of stacks
$C$-algebras. By definition there is an isomorphism of stacks
Similarly, we write ![]() $Z'\subset \operatorname {Lie} G\times G/P$ for the scheme parametrizing pairs
$Z'\subset \operatorname {Lie} G\times G/P$ for the scheme parametrizing pairs ![]() $(N,gP)$ such that
$(N,gP)$ such that ![]() $N\in {\rm Ad}(g^{-1})\operatorname {Lie} P$. Then
$N\in {\rm Ad}(g^{-1})\operatorname {Lie} P$. Then ![]() $Z'\rightarrow G/P$ is a vector bundle (with fibers isomorphic to
$Z'\rightarrow G/P$ is a vector bundle (with fibers isomorphic to ![]() $\operatorname {Lie} P$) and we can define
$\operatorname {Lie} P$) and we can define ![]() $\tilde {\mathbf {X}}_P$ as the derived fiber product
$\tilde {\mathbf {X}}_P$ as the derived fiber product

where ![]() $G/P\rightarrow Z'$ is the zero section and the right vertical arrow is the morphism given by
$G/P\rightarrow Z'$ is the zero section and the right vertical arrow is the morphism given by ![]() $(\varphi,N,gP)\mapsto ({\rm Ad}(\varphi )N-q^{-1}N,gP)$. Now
$(\varphi,N,gP)\mapsto ({\rm Ad}(\varphi )N-q^{-1}N,gP)$. Now ![]() $[\mathbf {X}_P/P]=[\tilde {\mathbf {X}}_P/G]\rightarrow [\mathbf {X}_G/G]$, and the projection
$[\mathbf {X}_P/P]=[\tilde {\mathbf {X}}_P/G]\rightarrow [\mathbf {X}_G/G]$, and the projection
is a ![]() $G$-equivariant model for the canonical projection
$G$-equivariant model for the canonical projection ![]() $[\mathbf {X}_P/P]\rightarrow [X_G/G]$ induced by
$[\mathbf {X}_P/P]\rightarrow [X_G/G]$ induced by ![]() $P\subset G$. The claim follows from this together with the observation that
$P\subset G$. The claim follows from this together with the observation that ![]() ${}^{\rm cl}\tilde {\mathbf {X}}_P=\tilde X_P$ and
${}^{\rm cl}\tilde {\mathbf {X}}_P=\tilde X_P$ and ![]() ${}^{\rm cl}[\mathbf {X}_P/P]=[X_P/P]$.
${}^{\rm cl}[\mathbf {X}_P/P]=[X_P/P]$.
(ii) This is a direct consequence of the definition of the fiber product in the category of dg-schemes and the fact that ![]() $P'$ is the pre-image of
$P'$ is the pre-image of ![]() $P'_M$ under the (flat) morphism
$P'_M$ under the (flat) morphism ![]() $P\rightarrow M$.
$P\rightarrow M$.
Remark 2.13 Let ![]() $B\subset G$ be a Borel subgroup and let
$B\subset G$ be a Borel subgroup and let ![]() $U\subset B$ denote the unipotent radical. Then
$U\subset B$ denote the unipotent radical. Then ![]() $\mathbf {X}_B\subset B\times \operatorname {Lie} B$ is in fact a (derived) subscheme of
$\mathbf {X}_B\subset B\times \operatorname {Lie} B$ is in fact a (derived) subscheme of ![]() $B\times \operatorname {Lie} U$. Indeed, computing
$B\times \operatorname {Lie} U$. Indeed, computing ![]() ${\rm Ad}(\varphi )N-q^{-1}N$ for the universal pair
${\rm Ad}(\varphi )N-q^{-1}N$ for the universal pair ![]() $(\varphi,N)$ over
$(\varphi,N)$ over ![]() $B\times \operatorname {Lie} B$ and restricting to the Lie algebra of (a choice of) a maximal torus in
$B\times \operatorname {Lie} B$ and restricting to the Lie algebra of (a choice of) a maximal torus in ![]() $B$, we find that
$B$, we find that ![]() $\mathbf {X}_B\subset B\times \operatorname {Lie} U$. Using this observation, we mention the following variant of the construction in the proof of (i) above. Letting
$\mathbf {X}_B\subset B\times \operatorname {Lie} U$. Using this observation, we mention the following variant of the construction in the proof of (i) above. Letting ![]() $\mathcal {N}_G$ denote the nilpotent cone of
$\mathcal {N}_G$ denote the nilpotent cone of ![]() $G$, we can define
$G$, we can define ![]() $Y=Z\cap G\times \mathcal {N}_G\times G/B$. In fact
$Y=Z\cap G\times \mathcal {N}_G\times G/B$. In fact ![]() $[Y/G]\cong [B\times \operatorname {Lie} U/B]$ and if we write
$[Y/G]\cong [B\times \operatorname {Lie} U/B]$ and if we write ![]() $\tilde {G}\rightarrow G$ (respectively,
$\tilde {G}\rightarrow G$ (respectively, ![]() $\tilde {\mathcal {N}}_G\rightarrow \mathcal {N}_G$) for the Grothendieck (respectively, Springer) resolution, then
$\tilde {\mathcal {N}}_G\rightarrow \mathcal {N}_G$) for the Grothendieck (respectively, Springer) resolution, then
In particular, ![]() $Y$ is smooth and affine of relative dimension
$Y$ is smooth and affine of relative dimension ![]() $\dim G$ over
$\dim G$ over ![]() $G/B$. Then we can define
$G/B$. Then we can define ![]() $\tilde {\mathbf {X}}_B$ as a closed sub-dg-scheme of
$\tilde {\mathbf {X}}_B$ as a closed sub-dg-scheme of ![]() $Y$ similarly to its definition as a closed sub-dg-scheme of
$Y$ similarly to its definition as a closed sub-dg-scheme of ![]() $Z$ in the proposition.
$Z$ in the proposition.
2.2 Derived categories of (quasi-)coherent sheaves
Given a scheme or a stack ![]() $X$ (or a derived scheme or a derived stack), we write
$X$ (or a derived scheme or a derived stack), we write ![]() ${\bf D}_{\rm QCoh}(X)$ for the derived category of quasi-coherent sheaves on
${\bf D}_{\rm QCoh}(X)$ for the derived category of quasi-coherent sheaves on ![]() $X$ (see [Reference Drinfeld and GaitsgoryDG13, 1.2] where it is denoted by
$X$ (see [Reference Drinfeld and GaitsgoryDG13, 1.2] where it is denoted by ![]() ${\rm QCoh}(X)$). We write
${\rm QCoh}(X)$). We write ![]() ${\bf D}^b_{\rm Coh}(X)$ for the full subcategory of objects that only have cohomology in finitely many degrees, which, moreover, is coherent.
${\bf D}^b_{\rm Coh}(X)$ for the full subcategory of objects that only have cohomology in finitely many degrees, which, moreover, is coherent.
If ![]() $X$ is a noetherian scheme then
$X$ is a noetherian scheme then ![]() ${\bf D}^b_{\rm Coh}(X)$ coincides with the full subcategory of the derived category
${\bf D}^b_{\rm Coh}(X)$ coincides with the full subcategory of the derived category ![]() ${\bf D}(\mathcal {O}_X\text {-mod})$ of
${\bf D}(\mathcal {O}_X\text {-mod})$ of ![]() $\mathcal {O}_X$-modules, consisting of those complexes that have coherent cohomology and whose cohomology is concentrated in finitely many degrees. Similarly, if
$\mathcal {O}_X$-modules, consisting of those complexes that have coherent cohomology and whose cohomology is concentrated in finitely many degrees. Similarly, if ![]() $X$ is a (classical) algebraic stack, then
$X$ is a (classical) algebraic stack, then ![]() ${\bf D}^b_{\rm Coh}(X)$, and more generally
${\bf D}^b_{\rm Coh}(X)$, and more generally ![]() ${\bf D}^+_{\rm QCoh}(X)$, agreesFootnote 3 with the definition of the bounded derived category of coherent sheaves, and, respectively, with the bounded-below derived category of quasi-coherent sheaves as defined in [Reference Laumon and Moret-BaillyLM00].
${\bf D}^+_{\rm QCoh}(X)$, agreesFootnote 3 with the definition of the bounded derived category of coherent sheaves, and, respectively, with the bounded-below derived category of quasi-coherent sheaves as defined in [Reference Laumon and Moret-BaillyLM00].
Lemma 2.14 Let ![]() $G$ be a reductive group and let
$G$ be a reductive group and let ![]() $P$ be a parabolic subgroup with Levi quotient
$P$ be a parabolic subgroup with Levi quotient ![]() $M$. Let
$M$. Let
denote the canonical morphisms. Then the maps
preserve the subcategories ![]() ${\bf D}^+_{\rm QCoh}(-)$ and
${\bf D}^+_{\rm QCoh}(-)$ and ![]() ${\bf D}^b_{\rm Coh}(-)$.
${\bf D}^b_{\rm Coh}(-)$.
Proof. In the case of ![]() $R\beta _\ast$ the claim directly follows from the fact that
$R\beta _\ast$ the claim directly follows from the fact that ![]() $\beta$ is proper and schematic. We prove the claim for
$\beta$ is proper and schematic. We prove the claim for ![]() $L\alpha ^\ast$. As the properties of belonging to
$L\alpha ^\ast$. As the properties of belonging to ![]() ${\bf D}^+_{\rm QCoh}(-)$ or
${\bf D}^+_{\rm QCoh}(-)$ or ![]() ${\bf D}^b_{\rm Coh}(-)$ can be checked over the smooth cover
${\bf D}^b_{\rm Coh}(-)$ can be checked over the smooth cover ![]() $\mathbf {X}_P$ of
$\mathbf {X}_P$ of ![]() $[\mathbf {X}_P/P]$, it is enough to show that pullback along the morphism
$[\mathbf {X}_P/P]$, it is enough to show that pullback along the morphism
preserves ![]() ${\bf D}^+_{\rm QCoh}(-)$ and
${\bf D}^+_{\rm QCoh}(-)$ and ![]() ${\bf D}^b_{\rm Coh}(-)$. Moreover, both properties may be checked after forgetting the
${\bf D}^b_{\rm Coh}(-)$. Moreover, both properties may be checked after forgetting the ![]() $\mathcal {O}_{\mathbf {X}_P}$-module structure, and only remembering the
$\mathcal {O}_{\mathbf {X}_P}$-module structure, and only remembering the ![]() $\mathcal {O}_{P\times \operatorname {Lie} P}$-module structure. As in the proof of Lemma 2.9, we find that
$\mathcal {O}_{P\times \operatorname {Lie} P}$-module structure. As in the proof of Lemma 2.9, we find that ![]() $\mathcal {O}_{\mathbf {X}_P}$ can be represented by a finite complex
$\mathcal {O}_{\mathbf {X}_P}$ can be represented by a finite complex ![]() $\mathcal {F}_P^\bullet$ of flat
$\mathcal {F}_P^\bullet$ of flat ![]() $\mathcal {O}_{\mathbf {X}_M}$-modules that are coherent as
$\mathcal {O}_{\mathbf {X}_M}$-modules that are coherent as ![]() $\mathcal {O}_{P\times \operatorname {Lie} P}$-modules, and
$\mathcal {O}_{P\times \operatorname {Lie} P}$-modules, and ![]() $L\alpha '^\ast$ is identified with the functor
$L\alpha '^\ast$ is identified with the functor ![]() $-\otimes ^{L}_{\mathcal {O}_{\mathbf {X}_M}}\mathcal {F}_P^\bullet$. The claim follows from this.
$-\otimes ^{L}_{\mathcal {O}_{\mathbf {X}_M}}\mathcal {F}_P^\bullet$. The claim follows from this.
Remark 2.15 (a) We point out that using the definition of the derived categories as in [Reference Drinfeld and GaitsgoryDG13] has the advantage that there is a canonical pullback functor between the derived categories of quasi-coherent sheaves on stacks. At least as long as we only consider non-derived stacks (such as ![]() $[X_G/G]$ or
$[X_G/G]$ or ![]() $[X_G^{\rm reg}/G]$) there is a definition of the derived category of quasi-coherent sheaves in [Reference Laumon and Moret-BaillyLM00]. However, the definition of the pullback functor in [Reference Laumon and Moret-BaillyLM00] encounters some problems. Lemma 2.14 essentially tells us that we could also use the definition of [Reference Laumon and Moret-BaillyLM00] and only consider complexes that are bounded below.
$[X_G^{\rm reg}/G]$) there is a definition of the derived category of quasi-coherent sheaves in [Reference Laumon and Moret-BaillyLM00]. However, the definition of the pullback functor in [Reference Laumon and Moret-BaillyLM00] encounters some problems. Lemma 2.14 essentially tells us that we could also use the definition of [Reference Laumon and Moret-BaillyLM00] and only consider complexes that are bounded below.
(b) The explicit description of the pullback in the proof of Lemma 2.14 could also be used to completely bypass the use of derived schemes, or derived stacks. In the end we will be interested in the composition ![]() $R\beta _\ast \circ L\alpha ^\ast$ rather than in the individual functors. Hence, instead of
$R\beta _\ast \circ L\alpha ^\ast$ rather than in the individual functors. Hence, instead of ![]() $L\alpha ^\ast$ we might use the construction
$L\alpha ^\ast$ we might use the construction ![]() $-\otimes ^L_{\mathcal {O}_{X_M}}\mathcal {F}^\bullet _P$ and carefully define the
$-\otimes ^L_{\mathcal {O}_{X_M}}\mathcal {F}^\bullet _P$ and carefully define the ![]() $\mathcal {O}_{[X_G/G]}$-action after push-forward (and after descent to the stack quotient). However, it seems to be more natural to use derived stacks than such an explicit workaround.
$\mathcal {O}_{[X_G/G]}$-action after push-forward (and after descent to the stack quotient). However, it seems to be more natural to use derived stacks than such an explicit workaround.
Let ![]() $P_1\subset P_2$ be parabolic subgroups of a reductive group
$P_1\subset P_2$ be parabolic subgroups of a reductive group ![]() $G$ with Levi quotients
$G$ with Levi quotients ![]() $M_i$,
$M_i$, ![]() $i=1,2$. We write
$i=1,2$. We write ![]() $P_{12}\subset M_2$ for the image of
$P_{12}\subset M_2$ for the image of ![]() $P_1$ in
$P_1$ in ![]() $M_2$. Then
$M_2$. Then ![]() $P_{12}\subset M_2$ is a parabolic subgroup with Levi quotient
$P_{12}\subset M_2$ is a parabolic subgroup with Levi quotient ![]() $M_1$. We obtain a diagram
$M_1$. We obtain a diagram

where the upper left diagram is cartesian (in the category of dg-stacks).
Lemma 2.16 In the above situation we have a natural isomorphism
of functors
Proof. The upper right square is (derived) cartesian and ![]() $\beta _{12}$ is schematic and proper; in particular, it is quasi-compact and quasi-separated. Hence, [Reference Drinfeld and GaitsgoryDG13, Propositions 1.3.6 and 1.3.10] implies that the natural base change morphism
$\beta _{12}$ is schematic and proper; in particular, it is quasi-compact and quasi-separated. Hence, [Reference Drinfeld and GaitsgoryDG13, Propositions 1.3.6 and 1.3.10] implies that the natural base change morphism
is an isomorphism. We obtain the natural isomorphism
 \begin{align*} & (R\beta_{2\,\ast}\circ L\alpha_{2}^\ast) \circ (R\beta_{12\,\ast}\circ L\alpha_{12}^\ast)=R\beta_{2\,\ast}\circ (L\alpha_{2}^\ast \circ R\beta_{12\,\ast})\circ L\alpha_{12}^\ast\\ &\quad \xrightarrow\cong R\beta_{2\,\ast}\circ (R\beta_\ast \circ L\alpha^\ast) \circ L\alpha_{12}^\ast =R\beta_{1\,\ast}\circ L\alpha_{1}^\ast. \end{align*}
\begin{align*} & (R\beta_{2\,\ast}\circ L\alpha_{2}^\ast) \circ (R\beta_{12\,\ast}\circ L\alpha_{12}^\ast)=R\beta_{2\,\ast}\circ (L\alpha_{2}^\ast \circ R\beta_{12\,\ast})\circ L\alpha_{12}^\ast\\ &\quad \xrightarrow\cong R\beta_{2\,\ast}\circ (R\beta_\ast \circ L\alpha^\ast) \circ L\alpha_{12}^\ast =R\beta_{1\,\ast}\circ L\alpha_{1}^\ast. \end{align*}
We point out that, working only with classical schemes, we still obtain a natural transformation between the corresponding functors: if we consider the underlying classical stacks in diagram (2.6) and keep the same notation for the morphisms by abuse of notation, then there still is a natural base change morphism, but it is not necessarily an isomorphism as the fiber product might not be Tor-independent. However, it becomes an isomorphism when we restrict the functors to the regular locus, that is, we consider them as functors
as in this case the classical and derived pictures coincide. Indeed, after the restriction to the regular locus the derived fiber product equals the classical fiber product by the Tor-independence in Lemma 2.9.
2.3 Duals
We continue to assume that ![]() $G$ is a reductive group over
$G$ is a reductive group over ![]() $C$ and fix a Borel subgroup
$C$ and fix a Borel subgroup ![]() $B\subset G$. Recall that we have defined a morphism
$B\subset G$. Recall that we have defined a morphism
of (derived) stacks. In this subsection we will analyze the (derived) direct image of the structure sheaf under this morphism, which will play an important roleFootnote 4 later on. For a (derived) scheme or a (derived) stack ![]() $X$ we will write
$X$ we will write ![]() $\omega _X\in {\bf D}_{\rm QCoh}(X)$ for the dualizing complex and
$\omega _X\in {\bf D}_{\rm QCoh}(X)$ for the dualizing complex and ![]() $\mathbb {D}_X(-)=R\mathcal {H}om_{\mathcal {O}_X}(-,\omega _X)$ for the usual duality functor. The main point of this section is to give evidence to the following conjecture (compare also [Reference Ben-Zvi, Chen, Helm and NadlerBCHN20, Conjecture 3.35] and [Reference ZhuZhu20, Conjecture 4.5.1 and Remark 4.5.4]).
$\mathbb {D}_X(-)=R\mathcal {H}om_{\mathcal {O}_X}(-,\omega _X)$ for the usual duality functor. The main point of this section is to give evidence to the following conjecture (compare also [Reference Ben-Zvi, Chen, Helm and NadlerBCHN20, Conjecture 3.35] and [Reference ZhuZhu20, Conjecture 4.5.1 and Remark 4.5.4]).
Conjecture 2.17 The derived direct image ![]() $R\beta _\ast (\mathcal {O}_{[\mathbf {X}_B/B]})\in {\bf D}_{\rm Coh}^b([X_G/G])$ is concentrated in degree zero and there is an isomorphism
$R\beta _\ast (\mathcal {O}_{[\mathbf {X}_B/B]})\in {\bf D}_{\rm Coh}^b([X_G/G])$ is concentrated in degree zero and there is an isomorphism
In particular, the pullback of ![]() $R\beta _\ast (\mathcal {O}_{[\mathbf {X}_B/B]})$ to
$R\beta _\ast (\mathcal {O}_{[\mathbf {X}_B/B]})$ to ![]() $X_G$ is concentrated in degree zero and is a maximal Cohen–Macaulay module.
$X_G$ is concentrated in degree zero and is a maximal Cohen–Macaulay module.
Let us write ![]() $\tilde \beta _B:\tilde {\mathbf {X}}_B\rightarrow X_G$ for the
$\tilde \beta _B:\tilde {\mathbf {X}}_B\rightarrow X_G$ for the ![]() $G$-equivariant model of
$G$-equivariant model of ![]() $\beta _B$, as in (2.5). The conjecture is obviously equivalent to the claim that
$\beta _B$, as in (2.5). The conjecture is obviously equivalent to the claim that ![]() $R\tilde \beta _{B,\ast }\mathcal {O}_{\tilde {\mathbf {X}}_B}$ is concentrated in degree zero and that there is a
$R\tilde \beta _{B,\ast }\mathcal {O}_{\tilde {\mathbf {X}}_B}$ is concentrated in degree zero and that there is a ![]() $G$-equivariant isomorphism
$G$-equivariant isomorphism
This isomorphism then implies that the dual of the sheaf ![]() $R\tilde \beta _{B,\ast }\mathcal {O}_{\tilde {\mathbf {X}}_B}$ is concentrated in a single degree and hence, by [Sta, Tag 0B5A], it is a Cohen–Macaulay module. As its support obviously is all of
$R\tilde \beta _{B,\ast }\mathcal {O}_{\tilde {\mathbf {X}}_B}$ is concentrated in a single degree and hence, by [Sta, Tag 0B5A], it is a Cohen–Macaulay module. As its support obviously is all of ![]() $X_G$ it is then a maximal Cohen–Macaulay module.
$X_G$ it is then a maximal Cohen–Macaulay module.
As in Remark 2.13, we write ![]() $Y\rightarrow G\times \operatorname {Lie} G$ for the scheme parametrizing triples
$Y\rightarrow G\times \operatorname {Lie} G$ for the scheme parametrizing triples ![]() $(\varphi,N,gB)\in G\times \mathcal {N}_G\times G/B$ such that
$(\varphi,N,gB)\in G\times \mathcal {N}_G\times G/B$ such that ![]() $\varphi \in g^{-1}Bg$ and
$\varphi \in g^{-1}Bg$ and ![]() $N\in {\rm Ad}(g^{-1})\operatorname {Lie} U$, where
$N\in {\rm Ad}(g^{-1})\operatorname {Lie} U$, where ![]() $U\subset B$ is the unipotent radical. Recall that
$U\subset B$ is the unipotent radical. Recall that ![]() $Y$ is smooth (of dimension
$Y$ is smooth (of dimension ![]() $\dim G+\dim G/B$) as the projection to the flag variety
$\dim G+\dim G/B$) as the projection to the flag variety ![]() $\operatorname {pr}:Y\rightarrow G/B$ is the composition of a
$\operatorname {pr}:Y\rightarrow G/B$ is the composition of a ![]() $B$-bundle and a geometric vector bundle (or rank
$B$-bundle and a geometric vector bundle (or rank ![]() $\dim U$). We consider the diagram
$\dim U$). We consider the diagram

and write ![]() $\mathcal {F}^\bullet =R\iota _{B,\ast }\mathcal {O}_{\tilde {\mathbf {X}}_B}$. The main observation is that
$\mathcal {F}^\bullet =R\iota _{B,\ast }\mathcal {O}_{\tilde {\mathbf {X}}_B}$. The main observation is that ![]() $\mathcal {F}^\bullet$ is represented by a Koszul complex and hence is self-dual (up to a shift). In order to make this precise, recall that an algebraic representation of
$\mathcal {F}^\bullet$ is represented by a Koszul complex and hence is self-dual (up to a shift). In order to make this precise, recall that an algebraic representation of ![]() $B$ defines a
$B$ defines a ![]() $G$-equivariant vector bundle on
$G$-equivariant vector bundle on ![]() $G/B$. We write
$G/B$. We write ![]() $\mathcal {U}^\vee$ for the
$\mathcal {U}^\vee$ for the ![]() $G$-equivariant vector bundle on
$G$-equivariant vector bundle on ![]() $G/B$ defined by the canonical
$G/B$ defined by the canonical ![]() $B$ representation on
$B$ representation on ![]() $\mathfrak {u}^\vee$. Here
$\mathfrak {u}^\vee$. Here ![]() $\mathfrak {u}$ denotes the Lie algebra of
$\mathfrak {u}$ denotes the Lie algebra of ![]() $U$ (considered as a
$U$ (considered as a ![]() $C$-vector space), and
$C$-vector space), and ![]() $\mathfrak {u}^\vee$ denotes its dual. In particular,
$\mathfrak {u}^\vee$ denotes its dual. In particular, ![]() $\mathcal {U}^\vee$ admits a filtration whose graded pieces are the line bundles
$\mathcal {U}^\vee$ admits a filtration whose graded pieces are the line bundles ![]() $\mathcal {L}_\alpha$ on
$\mathcal {L}_\alpha$ on ![]() $G/B$ associated to the negative (with respect to
$G/B$ associated to the negative (with respect to ![]() $B$) roots
$B$) roots ![]() $\alpha$ of
$\alpha$ of ![]() $G$.
$G$.
(i) The complex
 $\mathcal {F}^\bullet$ is represented by a Koszul complex
where the term
$\mathcal {F}^\bullet$ is represented by a Koszul complex
where the term \[ \cdots\longrightarrow \bigwedge\nolimits^i \operatorname{pr}^\ast(\mathcal{U}^\vee) \longrightarrow \bigwedge\nolimits^{i-1}\operatorname{pr}^\ast(\mathcal{U}^\vee)\longrightarrow\cdots \]
\[ \cdots\longrightarrow \bigwedge\nolimits^i \operatorname{pr}^\ast(\mathcal{U}^\vee) \longrightarrow \bigwedge\nolimits^{i-1}\operatorname{pr}^\ast(\mathcal{U}^\vee)\longrightarrow\cdots \]
 $\bigwedge \nolimits ^i \operatorname {pr}^\ast (\mathcal {U}^\vee )$ sits in (cohomological) degree
$\bigwedge \nolimits ^i \operatorname {pr}^\ast (\mathcal {U}^\vee )$ sits in (cohomological) degree  $-i$.
$-i$.(ii) There is a
 $G$-equivariant isomorphism
$G$-equivariant isomorphism
 \[ \mathcal{F}^\bullet\cong \mathbb{D}_{Y}(\mathcal{F}^\bullet)[-\dim G]. \]
\[ \mathcal{F}^\bullet\cong \mathbb{D}_{Y}(\mathcal{F}^\bullet)[-\dim G]. \]
Proof. (i) By definition the structure sheaf of the derived scheme ![]() $\mathbf {X}_B\subset B\times \operatorname {Lie} U$ is (as a complex of
$\mathbf {X}_B\subset B\times \operatorname {Lie} U$ is (as a complex of ![]() $\mathcal {O}_{B\times \operatorname {Lie} U}$-modules) quasi-isomorphic to the
$\mathcal {O}_{B\times \operatorname {Lie} U}$-modules) quasi-isomorphic to the ![]() $B$-equivariant Koszul complex
$B$-equivariant Koszul complex
defined by the entries of ![]() ${\rm Ad}(\varphi )N-q^{-1}N$ for the universal pair
${\rm Ad}(\varphi )N-q^{-1}N$ for the universal pair ![]() $(\varphi,N)$ over
$(\varphi,N)$ over ![]() $B\times \operatorname {Lie} U$ (where, by abuse of notation, we also write
$B\times \operatorname {Lie} U$ (where, by abuse of notation, we also write ![]() $\mathfrak {u}$ for the
$\mathfrak {u}$ for the ![]() $C$-vector space underlying the scheme
$C$-vector space underlying the scheme ![]() $\operatorname {Lie} U$). The claim follows from the identification
$\operatorname {Lie} U$). The claim follows from the identification ![]() $[Y/G]=[B\times \operatorname {Lie} U]$ (compare also Remark 2.13).
$[Y/G]=[B\times \operatorname {Lie} U]$ (compare also Remark 2.13).
(ii) The claim on duality follows from the usual self-duality of Koszul complexes which is induced by the perfect pairing
and the identification
Conjecture 2.19 The complex ![]() $Rf_\ast \mathcal {F}^\bullet$ is concentrated in non-negative degrees.
$Rf_\ast \mathcal {F}^\bullet$ is concentrated in non-negative degrees.
Proof. The morphisms ![]() $\iota _G$ and
$\iota _G$ and ![]() $f$ satisfy Grothendieck duality, as
$f$ satisfy Grothendieck duality, as ![]() $\iota _G$ is a complete intersection and
$\iota _G$ is a complete intersection and ![]() $f$ factors into a complete intersection and a smooth morphism. Hence, we have the following isomorphisms in
$f$ factors into a complete intersection and a smooth morphism. Hence, we have the following isomorphisms in ![]() ${\bf D}_{\rm QCoh}(G\times \mathfrak {g})$:
${\bf D}_{\rm QCoh}(G\times \mathfrak {g})$:
 \begin{align*} R\iota_{G,\ast}(R\tilde{\beta}_{B,\ast}(\mathcal{O}_{\tilde{\mathbf{X}}_B}))=Rf_\ast\mathcal{F}^\bullet &\cong Rf_\ast(\mathbb{D}_{Y}(\mathcal{F}^\bullet)[-\dim G])=Rf_\ast(\mathbb{D}_{Y} (\mathcal{F}^\bullet))[-\dim G]\\ &\cong \mathbb{D}_{G\times\mathfrak{g}}(Rf_\ast\mathcal{F}^\bullet)[-\dim G]\\ &=\mathbb{D}_{G\times\mathfrak{g}}(R\iota_{G,\ast}R\tilde{\beta}_{B,\ast} (\mathcal{O}_{\tilde{\mathbf{X}}_B}))[-\dim G]\\ &\cong R\iota_{G,\ast}(\mathbb{D}_{X_G}(R\tilde{\beta}_{B,\ast} (\mathcal{O}_{\tilde{\mathbf{X}}_B}))[-\dim G]). \end{align*}
\begin{align*} R\iota_{G,\ast}(R\tilde{\beta}_{B,\ast}(\mathcal{O}_{\tilde{\mathbf{X}}_B}))=Rf_\ast\mathcal{F}^\bullet &\cong Rf_\ast(\mathbb{D}_{Y}(\mathcal{F}^\bullet)[-\dim G])=Rf_\ast(\mathbb{D}_{Y} (\mathcal{F}^\bullet))[-\dim G]\\ &\cong \mathbb{D}_{G\times\mathfrak{g}}(Rf_\ast\mathcal{F}^\bullet)[-\dim G]\\ &=\mathbb{D}_{G\times\mathfrak{g}}(R\iota_{G,\ast}R\tilde{\beta}_{B,\ast} (\mathcal{O}_{\tilde{\mathbf{X}}_B}))[-\dim G]\\ &\cong R\iota_{G,\ast}(\mathbb{D}_{X_G}(R\tilde{\beta}_{B,\ast} (\mathcal{O}_{\tilde{\mathbf{X}}_B}))[-\dim G]). \end{align*}
Assuming Conjecture 2.19, the complex ![]() $Rf_\ast \mathcal {F}^\bullet$ is concentrated in degrees
$Rf_\ast \mathcal {F}^\bullet$ is concentrated in degrees ![]() $(-\infty,0]$, and hence so is
$(-\infty,0]$, and hence so is ![]() $R\tilde {\beta }_{B,\ast }(\mathcal {O}_{\tilde {\mathbf {X}}_B})$, as
$R\tilde {\beta }_{B,\ast }(\mathcal {O}_{\tilde {\mathbf {X}}_B})$, as ![]() $\iota _{G}$ is affine. It follows that
$\iota _{G}$ is affine. It follows that ![]() $\mathbb {D}_{X_G}(R\tilde {\beta }_{B,\ast }(\mathcal {O}_{\tilde {\mathbf {X}}_B}))$ is concentrated in degrees
$\mathbb {D}_{X_G}(R\tilde {\beta }_{B,\ast }(\mathcal {O}_{\tilde {\mathbf {X}}_B}))$ is concentrated in degrees ![]() $[-\dim G,+\infty )$ and hence
$[-\dim G,+\infty )$ and hence
is concentrated in degrees ![]() $[0,+\infty )$. Hence,
$[0,+\infty )$. Hence, ![]() $Rf_\ast \mathcal {F}^\bullet$ is concentrated in degree zero and, again using that
$Rf_\ast \mathcal {F}^\bullet$ is concentrated in degree zero and, again using that ![]() $\iota _G$ is affine, the same holds true for
$\iota _G$ is affine, the same holds true for ![]() $R\tilde {\beta }_{B,\ast }(\mathcal {O}_{\tilde {\mathbf {X}}_B})$.
$R\tilde {\beta }_{B,\ast }(\mathcal {O}_{\tilde {\mathbf {X}}_B})$.
But as ![]() $R\tilde {\beta }_{B,\ast }(\mathcal {O}_{\tilde {\mathbf {X}}_B})$ is concentrated in a single degree the isomorphism
$R\tilde {\beta }_{B,\ast }(\mathcal {O}_{\tilde {\mathbf {X}}_B})$ is concentrated in a single degree the isomorphism
is in fact a ![]() $G$-equivariant isomorphism of sheaves on
$G$-equivariant isomorphism of sheaves on ![]() $G\times \mathfrak {g}$ (not just an isomorphism in the derived category) and hence restricts to a
$G\times \mathfrak {g}$ (not just an isomorphism in the derived category) and hence restricts to a ![]() $G$-invariant isomorphism of sheaves
$G$-invariant isomorphism of sheaves
on ![]() $X_G$. As we have seen above, these claims are equivalent to Conjecture 2.17.
$X_G$. As we have seen above, these claims are equivalent to Conjecture 2.17.
Unfortunately we are not able to prove Conjecture 2.19 in general. We will instead give some evidence by proving the conjecture for ![]() ${\rm GL}_2$ and
${\rm GL}_2$ and ![]() ${\rm GL}_3$.
${\rm GL}_3$.
As ![]() $G\times \mathfrak {g}$ is affine it is enough to prove that
$G\times \mathfrak {g}$ is affine it is enough to prove that ![]() $H^i(G\times \mathfrak {g},Rf_\ast \mathcal {F}^\bullet )$ vanishes for
$H^i(G\times \mathfrak {g},Rf_\ast \mathcal {F}^\bullet )$ vanishes for ![]() $i>0$. This cohomology is computed by a spectral sequence
$i>0$. This cohomology is computed by a spectral sequence
and hence it is enough to show that ![]() $H^j(Y,\bigwedge \nolimits ^i\operatorname {pr}^\ast (\mathcal {U}^\vee ))=0\ \text {for}\ j>i$ (note that
$H^j(Y,\bigwedge \nolimits ^i\operatorname {pr}^\ast (\mathcal {U}^\vee ))=0\ \text {for}\ j>i$ (note that ![]() $\mathcal {F}^i=\bigwedge ^{-i}\operatorname {pr}^\ast (\mathcal {U}^\vee )$).
$\mathcal {F}^i=\bigwedge ^{-i}\operatorname {pr}^\ast (\mathcal {U}^\vee )$).
Proposition 2.21 Let ![]() $G={\rm GL}_2$ or
$G={\rm GL}_2$ or ![]() $G={\rm GL}_3$. Then
$G={\rm GL}_3$. Then
In particular, Conjecture 2.17 holds true for ![]() ${\rm GL}_2$ and
${\rm GL}_2$ and ![]() ${\rm GL}_3$.
${\rm GL}_3$.
Proof. We distinguish the cases ![]() $i>0$ and
$i>0$ and ![]() $i=0$. Let us prove the case
$i=0$. Let us prove the case ![]() $i>0$ first. We can compute this cohomology group after pushforward along the closed immersion
$i>0$ first. We can compute this cohomology group after pushforward along the closed immersion ![]() $Y\hookrightarrow G\times \mathcal {N}_G\times G/B$ as follows. Let us write
$Y\hookrightarrow G\times \mathcal {N}_G\times G/B$ as follows. Let us write ![]() $\bar {\mathcal {U}}$ (respectively,
$\bar {\mathcal {U}}$ (respectively, ![]() $\bar {\mathcal {B}}$) for
$\bar {\mathcal {B}}$) for ![]() $G$-equivariant vector bundles on
$G$-equivariant vector bundles on ![]() $G/B$ associated to the
$G/B$ associated to the ![]() $B$-representations on
$B$-representations on ![]() $\mathfrak {g}/\mathfrak {b}$ (respectively, on
$\mathfrak {g}/\mathfrak {b}$ (respectively, on ![]() $\mathfrak {g}/\mathfrak {u}$), where
$\mathfrak {g}/\mathfrak {u}$), where ![]() $\mathfrak {b}=\operatorname {Lie} B$. Note that
$\mathfrak {b}=\operatorname {Lie} B$. Note that ![]() $\mathcal {O}_Y$ is, as a sheaf on
$\mathcal {O}_Y$ is, as a sheaf on ![]() $G\times \mathcal {N}_G\times G/B$, quasi-isomorphic to the Koszul complex
$G\times \mathcal {N}_G\times G/B$, quasi-isomorphic to the Koszul complex
where again the ![]() $\bigwedge \nolimits ^i$ term appears in degree
$\bigwedge \nolimits ^i$ term appears in degree ![]() $-i$, and where
$-i$, and where ![]() $g:G\times \mathcal {N}_G\times G/B\rightarrow G/B$ denotes the canonical projection. By the projection formula (using that
$g:G\times \mathcal {N}_G\times G/B\rightarrow G/B$ denotes the canonical projection. By the projection formula (using that ![]() $g$ is affine and flat base change) we find that
$g$ is affine and flat base change) we find that
 \begin{align*} H^j(Y,\mathcal{F}^{-i})&=H^j\bigg(G\times\mathcal{N}_G\times G/B, \bigwedge\nolimits^ig^\ast(\mathcal{U})^\vee\otimes \mathcal{O}_Y\bigg)\\ &=H^j\bigg(G\times \mathcal{N}_G\times G/B, \bigwedge\nolimits^ig^\ast (\mathcal{U})^\vee\otimes \bigwedge\nolimits^\bullet g^\ast (\bar{\mathcal{U}}^\vee\otimes\bar{\mathcal{B}}^\vee)\bigg)\\ &=H^j\bigg(G/B,\bigwedge\nolimits^i\mathcal{U}^\vee\otimes \bigwedge\nolimits^\bullet (\bar{\mathcal{U}}^\vee\otimes \bar{\mathcal{B}}^\vee)\bigg)\otimes_C \Gamma(G\times \mathcal{N}_G,\mathcal{O}_{G\times\mathcal{N}}) \end{align*}
\begin{align*} H^j(Y,\mathcal{F}^{-i})&=H^j\bigg(G\times\mathcal{N}_G\times G/B, \bigwedge\nolimits^ig^\ast(\mathcal{U})^\vee\otimes \mathcal{O}_Y\bigg)\\ &=H^j\bigg(G\times \mathcal{N}_G\times G/B, \bigwedge\nolimits^ig^\ast (\mathcal{U})^\vee\otimes \bigwedge\nolimits^\bullet g^\ast (\bar{\mathcal{U}}^\vee\otimes\bar{\mathcal{B}}^\vee)\bigg)\\ &=H^j\bigg(G/B,\bigwedge\nolimits^i\mathcal{U}^\vee\otimes \bigwedge\nolimits^\bullet (\bar{\mathcal{U}}^\vee\otimes \bar{\mathcal{B}}^\vee)\bigg)\otimes_C \Gamma(G\times \mathcal{N}_G,\mathcal{O}_{G\times\mathcal{N}}) \end{align*}
and again we can use a spectral sequence to compute this cohomology group. Hence, it is enough to show that
As ![]() $\bar {\mathcal {B}}^\vee$ is an extension of
$\bar {\mathcal {B}}^\vee$ is an extension of ![]() $\bar {\mathcal {U}}^\vee$ and a power of the trivial line bundle it is enough to prove that
$\bar {\mathcal {U}}^\vee$ and a power of the trivial line bundle it is enough to prove that
We compute this cohomology group in terms of the cohomology of equivariant line bundles: note that the ![]() $G$-equivariant vector bundle
$G$-equivariant vector bundle ![]() $\bigwedge \nolimits ^a\mathcal {U}^\vee \otimes \bigwedge \nolimits ^b \bar {\mathcal {U}}^\vee \otimes \bigwedge \nolimits ^c\bar {\mathcal {U}}^\vee$ has a filtration whose subquotients are
$\bigwedge \nolimits ^a\mathcal {U}^\vee \otimes \bigwedge \nolimits ^b \bar {\mathcal {U}}^\vee \otimes \bigwedge \nolimits ^c\bar {\mathcal {U}}^\vee$ has a filtration whose subquotients are ![]() $G$-equivariant lines bundles
$G$-equivariant lines bundles ![]() $\mathcal {L}_{\lambda }\otimes \mathcal {L}_\mu \otimes \mathcal {L}_\nu =\mathcal {L}_{\lambda +\mu +\nu }$, where
$\mathcal {L}_{\lambda }\otimes \mathcal {L}_\mu \otimes \mathcal {L}_\nu =\mathcal {L}_{\lambda +\mu +\nu }$, where ![]() $\lambda$ is a sum of
$\lambda$ is a sum of ![]() $a$ pairwise distinct positive roots,Footnote 5
$a$ pairwise distinct positive roots,Footnote 5 ![]() $\mu$ is a sum of
$\mu$ is a sum of ![]() $b$ pairwise distinct negative roots and
$b$ pairwise distinct negative roots and ![]() $\nu$ is a sum of
$\nu$ is a sum of ![]() $c$ pairwise distinct negative roots. It hence suffices to show that
$c$ pairwise distinct negative roots. It hence suffices to show that ![]() $H^\bullet (G/B,\mathcal {L}_{\lambda +\mu +\nu })$ vanishes in degrees higher than
$H^\bullet (G/B,\mathcal {L}_{\lambda +\mu +\nu })$ vanishes in degrees higher than ![]() $a+b+c$ in this case. By the Borel–Bott–Weil theorem the cohomology of these line bundles is computed as follows. We write
$a+b+c$ in this case. By the Borel–Bott–Weil theorem the cohomology of these line bundles is computed as follows. We write ![]() $w\cdot \kappa =w(\kappa +\rho )-\rho$ for the dot action of the Weyl group
$w\cdot \kappa =w(\kappa +\rho )-\rho$ for the dot action of the Weyl group ![]() $W$ on
$W$ on ![]() $X^\ast (T)$, where
$X^\ast (T)$, where ![]() $\rho$ is the half sum of the positive roots. Then there is either an element
$\rho$ is the half sum of the positive roots. Then there is either an element ![]() $1\neq w\in W$ such that
$1\neq w\in W$ such that ![]() $w\cdot \kappa =\kappa$, or a unique
$w\cdot \kappa =\kappa$, or a unique ![]() $w\in W$ such that
$w\in W$ such that ![]() $w\cdot \kappa$ is dominant. In the first case
$w\cdot \kappa$ is dominant. In the first case ![]() $H^\bullet (G/B,\mathcal {L}_{\kappa })=0$ and in the second case
$H^\bullet (G/B,\mathcal {L}_{\kappa })=0$ and in the second case ![]() $H^\bullet (G/B,\mathcal {L}_{\kappa })$ is an irreducible
$H^\bullet (G/B,\mathcal {L}_{\kappa })$ is an irreducible ![]() $G$-representation concentrated in degree
$G$-representation concentrated in degree ![]() $\ell (w)$, where, as usual,
$\ell (w)$, where, as usual, ![]() $\ell (w)$ denotes the length of the Weyl group element
$\ell (w)$ denotes the length of the Weyl group element ![]() $w$. We hence obtain a combinatorial claim about roots which allows us to check the vanishing of
$w$. We hence obtain a combinatorial claim about roots which allows us to check the vanishing of ![]() $H^j(Y,\bigwedge \nolimits ^i\operatorname {pr}^\ast (\mathcal {U}^\vee ))$.
$H^j(Y,\bigwedge \nolimits ^i\operatorname {pr}^\ast (\mathcal {U}^\vee ))$.
Recall that we are assuming ![]() $i>0$. The above discussion implies that it is enough to prove the following claim. Let
$i>0$. The above discussion implies that it is enough to prove the following claim. Let ![]() $a\geq 1$ and
$a\geq 1$ and ![]() $b,c\geq 0$ and let
$b,c\geq 0$ and let ![]() $\lambda$ be a sum of
$\lambda$ be a sum of ![]() $a$ pairwise distinct positive roots,
$a$ pairwise distinct positive roots, ![]() $\mu$ be a sum of
$\mu$ be a sum of ![]() $b$ pairwise distinct negative roots and
$b$ pairwise distinct negative roots and ![]() $\nu$ be a sum of
$\nu$ be a sum of ![]() $c$ pairwise distinct negative roots. If there is some (necessarily unique)
$c$ pairwise distinct negative roots. If there is some (necessarily unique) ![]() $w\in W$ such that
$w\in W$ such that ![]() $w\cdot (\lambda +\mu +\nu )$ is dominant, then
$w\cdot (\lambda +\mu +\nu )$ is dominant, then ![]() $\ell (w)\leq a+b+c$.
$\ell (w)\leq a+b+c$.
In the ![]() ${\rm GL}_2$ case this computation is rather trivial. In the
${\rm GL}_2$ case this computation is rather trivial. In the ![]() ${\rm GL}_3$ case
${\rm GL}_3$ case ![]() $G/B$ has dimension three and the claim is trivially satisfied for
$G/B$ has dimension three and the claim is trivially satisfied for ![]() $a+b+c\geq 3$. We are left to check the cases
$a+b+c\geq 3$. We are left to check the cases ![]() $a+b+c=1$ and
$a+b+c=1$ and ![]() $a+b+c=2$.
$a+b+c=2$.
We write ![]() $\alpha$ and
$\alpha$ and ![]() $\beta$ for the two simple positive roots, and
$\beta$ for the two simple positive roots, and ![]() $s_\alpha,s_\beta \in W$ for the corresponding reflections.
$s_\alpha,s_\beta \in W$ for the corresponding reflections.
In the case ![]() $a+b+c=1$ the condition
$a+b+c=1$ the condition ![]() $a\geq 1$ implies
$a\geq 1$ implies ![]() $b=c=0$, and hence we need to check that
$b=c=0$, and hence we need to check that ![]() $\mathcal {L}_\alpha,\mathcal {L}_\beta$ and
$\mathcal {L}_\alpha,\mathcal {L}_\beta$ and ![]() $\mathcal {L}_{\alpha +\beta }$ have cohomology only in degree
$\mathcal {L}_{\alpha +\beta }$ have cohomology only in degree ![]() $\leq 1$. In the case
$\leq 1$. In the case ![]() $a+b+c=2$ we need to check the cases
$a+b+c=2$ we need to check the cases ![]() $a=b=1, c=0$ (the case
$a=b=1, c=0$ (the case ![]() $a=c=1, b=0$ of course being equivalent to this case) and
$a=c=1, b=0$ of course being equivalent to this case) and ![]() $a=2, b=c=0$. We hence need to show that the line bundles
$a=2, b=c=0$. We hence need to show that the line bundles
have cohomology only in degrees ![]() $\leq 2$.
$\leq 2$.
More precisely, we have to check that for any of these weights ![]() $\kappa$, either
$\kappa$, either ![]() $\kappa$ is fixed by some
$\kappa$ is fixed by some ![]() ${1\neq w}$ under the dot action, or
${1\neq w}$ under the dot action, or ![]() $w\cdot \kappa$ is dominant for some
$w\cdot \kappa$ is dominant for some ![]() $w$ of length less than or equal to
$w$ of length less than or equal to ![]() $2$. This is done Table 1.
$2$. This is done Table 1.
Table 1. The dot-action on sums of roots, I.

We are left to prove the proposition in the case ![]() $i=0$, that is, we need to show that
$i=0$, that is, we need to show that ![]() $H^\bullet (Y,\mathcal {O}_Y)$ vanishes in positive degrees. Using the same criterion as above, we calculate
$H^\bullet (Y,\mathcal {O}_Y)$ vanishes in positive degrees. Using the same criterion as above, we calculate ![]() $\mathcal {O}_Y$ as a Koszul complex which reduces us to proving that
$\mathcal {O}_Y$ as a Koszul complex which reduces us to proving that
In the case ![]() $G={\rm GL}_2$ this is again trivially satisfied. In the case
$G={\rm GL}_2$ this is again trivially satisfied. In the case ![]() $G={\rm GL}_3$ this means we need to prove that
$G={\rm GL}_3$ this means we need to prove that ![]() $H^\bullet (G/B,\bar {\mathcal {U}}^\vee )$ vanishes in degrees higher than
$H^\bullet (G/B,\bar {\mathcal {U}}^\vee )$ vanishes in degrees higher than ![]() $1$ and
$1$ and ![]() $H^\bullet (G/B,\bar {\mathcal {U}}^\vee \otimes \bar {\mathcal {U}}^\vee )$ vanishes in degrees
$H^\bullet (G/B,\bar {\mathcal {U}}^\vee \otimes \bar {\mathcal {U}}^\vee )$ vanishes in degrees ![]() $>2$. We hence need to compute the cohomology of the lines bundles
$>2$. We hence need to compute the cohomology of the lines bundles
Using Borel–Bott–Weil again, these cohomologies are computed using Table 2, where ![]() $w_0=s_\alpha s_\beta s_\alpha$ is the longest element. It is a direct consequence that the cohomology
$w_0=s_\alpha s_\beta s_\alpha$ is the longest element. It is a direct consequence that the cohomology ![]() $H^\bullet (G/B,\bar {\mathcal {U}}^\vee )$ is concentrated in degrees less than or equal to
$H^\bullet (G/B,\bar {\mathcal {U}}^\vee )$ is concentrated in degrees less than or equal to ![]() $1$, whereas the cohomology
$1$, whereas the cohomology ![]() $H^\bullet (G/B,\bar {\mathcal {U}}^\vee \otimes \bar {\mathcal {U}}^\vee )$ is concentrated in degrees less than or equal to
$H^\bullet (G/B,\bar {\mathcal {U}}^\vee \otimes \bar {\mathcal {U}}^\vee )$ is concentrated in degrees less than or equal to ![]() $2$ if and only if the boundary map
$2$ if and only if the boundary map
is surjective (or equivalently non-zero as the target of the map is an irreducible ![]() $G$-representation). By Serre duality this is equivalent to the injectivity of the induced map
$G$-representation). By Serre duality this is equivalent to the injectivity of the induced map
But this map is the boundary map in cohomology induced by a non-split extension
The fact that this extension is non-split implies that
is the zero map (as ![]() $\mathcal {L}_0$ is the trivial line bundle the canonical map
$\mathcal {L}_0$ is the trivial line bundle the canonical map ![]() $\Gamma (G/B,\mathcal {L}_0)\otimes \mathcal {O}_{G/B}\rightarrow \mathcal {L}_0$ is an isomorphism, and if
$\Gamma (G/B,\mathcal {L}_0)\otimes \mathcal {O}_{G/B}\rightarrow \mathcal {L}_0$ is an isomorphism, and if ![]() $H^0(G/B,\mathcal {E})\longrightarrow H^0(G/B, \mathcal {L}_{0})$ was non-zero it necessarily would be an isomorphism which would imply that the canonical map
$H^0(G/B,\mathcal {E})\longrightarrow H^0(G/B, \mathcal {L}_{0})$ was non-zero it necessarily would be an isomorphism which would imply that the canonical map ![]() $\Gamma (G/B,\mathcal {E})\otimes \mathcal {O}_{G/B}\rightarrow \mathcal {E}$ would induce a splitting of (2.9)) which in turn implies that (2.8) is injective. It follows that
$\Gamma (G/B,\mathcal {E})\otimes \mathcal {O}_{G/B}\rightarrow \mathcal {E}$ would induce a splitting of (2.9)) which in turn implies that (2.8) is injective. It follows that ![]() $H^\bullet (Y,\mathcal {O}_Y)=0$ for
$H^\bullet (Y,\mathcal {O}_Y)=0$ for ![]() $\bullet >0$ as claimed.
$\bullet >0$ as claimed.
Table 2. The dot-action on sums of roots, II.

Remark 2.22 Though this computation can be carried out for ![]() ${\rm GL}_2$ and
${\rm GL}_2$ and ![]() ${\rm GL}_3$ rather explicitly it seems that these computations (using Borel–Bott–Weil and boundary maps) become extremely difficult in higher dimensions. Indeed, it is combinatorially involved to understand in what degrees certain line bundles have non-vanishing cohomology, and in addition we would need to understand certain boundary maps in long exact sequences.
${\rm GL}_3$ rather explicitly it seems that these computations (using Borel–Bott–Weil and boundary maps) become extremely difficult in higher dimensions. Indeed, it is combinatorially involved to understand in what degrees certain line bundles have non-vanishing cohomology, and in addition we would need to understand certain boundary maps in long exact sequences.
Remark 2.23 Even though we cannot prove Conjecture 2.17 in general, it follows that the restriction of ![]() $R\tilde \beta _{B,\ast }(\mathcal {O}_{\tilde {\mathbf {X}}_B})$ to the regular locus
$R\tilde \beta _{B,\ast }(\mathcal {O}_{\tilde {\mathbf {X}}_B})$ to the regular locus ![]() $X^{\rm reg}_G\subset X_G$ is a maximal Cohen–Macaulay module. In particular, is it flat in the neighborhood of points
$X^{\rm reg}_G\subset X_G$ is a maximal Cohen–Macaulay module. In particular, is it flat in the neighborhood of points ![]() $x=(\varphi,N)\in X^{\rm reg}_G$ such that
$x=(\varphi,N)\in X^{\rm reg}_G$ such that ![]() $X_G$ is smooth at
$X_G$ is smooth at ![]() $x$, by the Auslander–Buchsbaum formula. For
$x$, by the Auslander–Buchsbaum formula. For ![]() $G=\operatorname {GL}_n$ this is the case if
$G=\operatorname {GL}_n$ this is the case if ![]() $(\varphi ^{\rm ss},N)$ is the L-parameter of a generic representation (see [Reference Barnet-Lamb, Gee, Geraghty and TaylorBGGT14, Lemma 1.3.2.(1)]). For a parabolic subgroup
$(\varphi ^{\rm ss},N)$ is the L-parameter of a generic representation (see [Reference Barnet-Lamb, Gee, Geraghty and TaylorBGGT14, Lemma 1.3.2.(1)]). For a parabolic subgroup ![]() $P\subset G$ the morphism
$P\subset G$ the morphism ![]() $\beta _P:\tilde X_P\rightarrow X_G$ is clearly not flat in general, as its fiber dimension can jump. And even the finite morphism
$\beta _P:\tilde X_P\rightarrow X_G$ is clearly not flat in general, as its fiber dimension can jump. And even the finite morphism ![]() $\tilde X_P^{\rm reg}\rightarrow X_G^{\rm reg}$ is not flat: at the intersection points of two irreducible components of
$\tilde X_P^{\rm reg}\rightarrow X_G^{\rm reg}$ is not flat: at the intersection points of two irreducible components of ![]() $X_G^{\rm reg}$ the number of points in the fiber (counted with multiplicity) can jump.
$X_G^{\rm reg}$ the number of points in the fiber (counted with multiplicity) can jump.
3. Smooth representations and modules over the Iwahori–Hecke algebra
Let ![]() $F$ be a finite extension of
$F$ be a finite extension of ![]() $\mathbb {Q}_p$ (or of
$\mathbb {Q}_p$ (or of ![]() $\mathbb {F}_p(\!(t)\!)$) with residue field
$\mathbb {F}_p(\!(t)\!)$) with residue field ![]() $k_F$ and let
$k_F$ and let ![]() $q=p^r=|k_F|$. In the following let
$q=p^r=|k_F|$. In the following let ![]() $\mathbb {G}$ be a split reductive group over
$\mathbb {G}$ be a split reductive group over ![]() $F$ and write
$F$ and write ![]() $G=\mathbb {G}(F)$. From now on we will assume that
$G=\mathbb {G}(F)$. From now on we will assume that ![]() $C$ contains a square root
$C$ contains a square root ![]() $q^{1/2}$ of
$q^{1/2}$ of ![]() $q$. We fix a choice of this root.
$q$. We fix a choice of this root.
We will always fix ![]() $\mathbb {T}\subset \mathbb {B}\subset \mathbb {G}$, a split maximal torus and a Borel subgroup. By this choice we can define the dual group
$\mathbb {T}\subset \mathbb {B}\subset \mathbb {G}$, a split maximal torus and a Borel subgroup. By this choice we can define the dual group ![]() $\check G$ of
$\check G$ of ![]() $G$ considered as an algebraic group over
$G$ considered as an algebraic group over ![]() $C$. Moreover, we denote by
$C$. Moreover, we denote by ![]() $\check T\subset \check B\subset \check G$ the dual torus and the dual Borel. More generally, given a parabolic subgroup
$\check T\subset \check B\subset \check G$ the dual torus and the dual Borel. More generally, given a parabolic subgroup ![]() $\mathbb {P}\subset \mathbb {G}$ containing
$\mathbb {P}\subset \mathbb {G}$ containing ![]() $\mathbb {B}$, we denote by
$\mathbb {B}$, we denote by ![]() $\check P\subset \check G$ the corresponding parabolic subgroup of the dual group. We write
$\check P\subset \check G$ the corresponding parabolic subgroup of the dual group. We write ![]() $W=W_G=W(\mathbb {G},\mathbb {T})$ for the Weyl group of
$W=W_G=W(\mathbb {G},\mathbb {T})$ for the Weyl group of ![]() $(\mathbb {G},\mathbb {T})$. If
$(\mathbb {G},\mathbb {T})$. If ![]() $\mathbb {P}\subset \mathbb {G}$ is a parabolic subgroup containing
$\mathbb {P}\subset \mathbb {G}$ is a parabolic subgroup containing ![]() $\mathbb {B}$, then the choice of
$\mathbb {B}$, then the choice of ![]() $\mathbb {T}$ defines a lifting of the Levi quotient
$\mathbb {T}$ defines a lifting of the Levi quotient ![]() $\mathbb {M}$ of
$\mathbb {M}$ of ![]() $\mathbb {P}$ to a subgroup of
$\mathbb {P}$ to a subgroup of ![]() $\mathbb {G}$. Similarly, we regard the dual group
$\mathbb {G}$. Similarly, we regard the dual group ![]() $\check M$ of
$\check M$ of ![]() $\mathbb {M}$ as a subgroup of
$\mathbb {M}$ as a subgroup of ![]() $\check G$ containing the maximal torus
$\check G$ containing the maximal torus ![]() $\check T$. We write
$\check T$. We write ![]() $W_M\subset W$ for the Weyl group of
$W_M\subset W$ for the Weyl group of ![]() $(\mathbb {M},\mathbb {T})$.
$(\mathbb {M},\mathbb {T})$.
Let ![]() $\check G/\hspace {-.1cm}/\check G$ denote the GIT quotient of
$\check G/\hspace {-.1cm}/\check G$ denote the GIT quotient of ![]() $\check G$ with respect to its adjoint action on itself. The inclusion
$\check G$ with respect to its adjoint action on itself. The inclusion ![]() $\check T\hookrightarrow \check G$ induces an isomorphism
$\check T\hookrightarrow \check G$ induces an isomorphism ![]() $\check T/W\cong \check G/\hspace {-.1cm}/\check G$. The projection
$\check T/W\cong \check G/\hspace {-.1cm}/\check G$. The projection ![]() $X_{\check G}\rightarrow {\check G}$ induces a map
$X_{\check G}\rightarrow {\check G}$ induces a map
which is ![]() $\check G$-equivariant and hence induces a map
$\check G$-equivariant and hence induces a map ![]() $\bar \chi =\bar \chi _{G}:[X_{\check G}/\check G]\rightarrow \check T/W$. Similarly, we obtain morphisms
$\bar \chi =\bar \chi _{G}:[X_{\check G}/\check G]\rightarrow \check T/W$. Similarly, we obtain morphisms
3.1 Categories of smooth representations
Let us write ![]() ${\rm Rep}(G)$ for the category of smooth representations of
${\rm Rep}(G)$ for the category of smooth representations of ![]() $G$ on
$G$ on ![]() $C$ vector spaces. It is well known that
$C$ vector spaces. It is well known that ![]() ${\rm Rep}(G)$ has a decomposition into Bernstein blocks
${\rm Rep}(G)$ has a decomposition into Bernstein blocks
where ![]() $\Omega (G)$ is a set of equivalence classes of a Levi
$\Omega (G)$ is a set of equivalence classes of a Levi ![]() $M$ of
$M$ of ![]() $G$ and a cuspidal representation
$G$ and a cuspidal representation ![]() $\sigma$ of
$\sigma$ of ![]() $M$ (see [Reference BernsteinBer92, III, 2.2], for example). We will restrict our attention to the Bernstein component
$M$ (see [Reference BernsteinBer92, III, 2.2], for example). We will restrict our attention to the Bernstein component ![]() ${\rm Rep}_{[T,1]}(G)$, where
${\rm Rep}_{[T,1]}(G)$, where ![]() $1$ is the trivial representation of the torus
$1$ is the trivial representation of the torus ![]() $T$. Given
$T$. Given ![]() $\pi \in {\rm Rep}(G)$ we write
$\pi \in {\rm Rep}(G)$ we write ![]() $\pi _{[T,1]}$ for its image under the projection to
$\pi _{[T,1]}$ for its image under the projection to ![]() ${\rm Rep}_{[T,1]}(G)$. Moreover, we will write
${\rm Rep}_{[T,1]}(G)$. Moreover, we will write ![]() $\mathfrak {Z}_G$ for the center of the category
$\mathfrak {Z}_G$ for the center of the category ![]() ${\rm Rep}_{[T,1]}(G)$; then
${\rm Rep}_{[T,1]}(G)$; then
(see below for an explicit description). This isomorphism allows us to identify the category ![]() $\mathfrak {Z}_G\text {-mod}$ of
$\mathfrak {Z}_G\text {-mod}$ of ![]() $\mathfrak {Z}_G$-modules with the category
$\mathfrak {Z}_G$-modules with the category ![]() ${\rm QCoh}(\check T/W)$ of quasi-coherent sheaves on the adjoint quotient
${\rm QCoh}(\check T/W)$ of quasi-coherent sheaves on the adjoint quotient ![]() $\check G/\hspace {-0.1cm}/\check G=\check T/W$ of
$\check G/\hspace {-0.1cm}/\check G=\check T/W$ of ![]() $\check G$, and the category
$\check G$, and the category ![]() $\mathfrak {Z}_G\text {-mod}_{\rm fg}$ of finitely generated
$\mathfrak {Z}_G\text {-mod}_{\rm fg}$ of finitely generated ![]() $\mathfrak {Z}_G$-modules with the category
$\mathfrak {Z}_G$-modules with the category ![]() ${\rm Coh}(\check T/W)$ of coherent sheaves on
${\rm Coh}(\check T/W)$ of coherent sheaves on ![]() $\check T/W$. We obtain an identification of derived categories
$\check T/W$. We obtain an identification of derived categories
 \begin{equation} \begin{aligned} {\bf D}(\mathfrak{Z}_G\text{-mod}) & \cong {\bf D}_{\rm QCoh}(\check T/W),\\ {\bf D}^b(\mathfrak{Z}_G\text{-mod}_{\text{fg}}) & \cong {\bf D}^b_{\rm Coh}(\check T/W). \end{aligned} \end{equation}
\begin{equation} \begin{aligned} {\bf D}(\mathfrak{Z}_G\text{-mod}) & \cong {\bf D}_{\rm QCoh}(\check T/W),\\ {\bf D}^b(\mathfrak{Z}_G\text{-mod}_{\text{fg}}) & \cong {\bf D}^b_{\rm Coh}(\check T/W). \end{aligned} \end{equation}
We use these identifications and the morphism ![]() $\bar \chi :[X_{\check G}/\check G]\rightarrow \check T/W$ to make
$\bar \chi :[X_{\check G}/\check G]\rightarrow \check T/W$ to make ![]() ${\bf D}^+_{\rm QCoh}([X_{\check G}/\check G])$ and
${\bf D}^+_{\rm QCoh}([X_{\check G}/\check G])$ and ![]() ${\bf D}^b_{\rm Coh}([X_{\check G}/\check G])$ into
${\bf D}^b_{\rm Coh}([X_{\check G}/\check G])$ into ![]() $\mathfrak {Z}_G$-linear categories.
$\mathfrak {Z}_G$-linear categories.
If ![]() $\mathbb {P}\subset \mathbb {G}$ is a parabolic subgroup with Levi quotient
$\mathbb {P}\subset \mathbb {G}$ is a parabolic subgroup with Levi quotient ![]() $\mathbb {M}$, we write
$\mathbb {M}$, we write
for the normalized parabolic induction, and ![]() $\iota _{\overline {P}}^G$ for normalized parabolic induction of the opposite parabolic
$\iota _{\overline {P}}^G$ for normalized parabolic induction of the opposite parabolic ![]() $\overline {P}$ of
$\overline {P}$ of ![]() $P$ (note that the normalization uses the choice of
$P$ (note that the normalization uses the choice of ![]() $q^{1/2}$). These functors are exact and restrict to functors
$q^{1/2}$). These functors are exact and restrict to functors
(for any choice of a maximal split torus ![]() $T_M$ of
$T_M$ of ![]() $M$). Using a splitting
$M$). Using a splitting ![]() $\mathbb {M}\hookrightarrow \mathbb {P}\subset \mathbb {G}$ to the projection, we obtain a morphism
$\mathbb {M}\hookrightarrow \mathbb {P}\subset \mathbb {G}$ to the projection, we obtain a morphism
which is obviously independent of the choice of ![]() $\mathbb {M}\hookrightarrow \mathbb {G}$. Then the functors
$\mathbb {M}\hookrightarrow \mathbb {G}$. Then the functors ![]() $\iota _P^G$ and
$\iota _P^G$ and ![]() $\iota _{\overline {P}}^G$ are linear with respect to the morphism
$\iota _{\overline {P}}^G$ are linear with respect to the morphism
(see below for details).
Let us write ![]() ${\bf D}({\rm Rep}_{[T,1]}(G))$ (respectively,
${\bf D}({\rm Rep}_{[T,1]}(G))$ (respectively, ![]() ${\bf D}^+({\rm Rep}_{[T,1]}(G))$) for the derived category (respectively, for the bounded-below derived category) of
${\bf D}^+({\rm Rep}_{[T,1]}(G))$) for the derived category (respectively, for the bounded-below derived category) of ![]() ${\rm Rep}_{[T,1]}(G)$. Moreover, we write
${\rm Rep}_{[T,1]}(G)$. Moreover, we write ![]() ${\bf D}^b({\rm Rep}_{[T,1],{\rm fg}}(G))$ for the full subcategory of complexes whose cohomology is concentrated in bounded degrees and is finitely generated as a
${\bf D}^b({\rm Rep}_{[T,1],{\rm fg}}(G))$ for the full subcategory of complexes whose cohomology is concentrated in bounded degrees and is finitely generated as a ![]() $C[G]$-module. Then
$C[G]$-module. Then ![]() $\iota _P^G$ (respectively,
$\iota _P^G$ (respectively, ![]() $\iota _{\overline {P}}^G$) induce functors
$\iota _{\overline {P}}^G$) induce functors
 \begin{align*} {\bf D}({\rm Rep}_{[T_M,1]}(M))&\longrightarrow {\bf D}({\rm Rep}_{[T,1]}(G)),\\ {\bf D}^+({\rm Rep}_{[T_M,1]}(M))&\longrightarrow {\bf D}^+({\rm Rep}_{[T,1]}(G)),\\ {\bf D}^b({\rm Rep}_{[T_M,1],{\rm fg}}(M))&\longrightarrow {\bf D}^b({\rm Rep}_{[T,1],{\rm fg}}(G)), \end{align*}
\begin{align*} {\bf D}({\rm Rep}_{[T_M,1]}(M))&\longrightarrow {\bf D}({\rm Rep}_{[T,1]}(G)),\\ {\bf D}^+({\rm Rep}_{[T_M,1]}(M))&\longrightarrow {\bf D}^+({\rm Rep}_{[T,1]}(G)),\\ {\bf D}^b({\rm Rep}_{[T_M,1],{\rm fg}}(M))&\longrightarrow {\bf D}^b({\rm Rep}_{[T,1],{\rm fg}}(G)), \end{align*}
which we will also denote by ![]() $\iota _P^G$ (respectively,
$\iota _P^G$ (respectively, ![]() $\iota _{\overline {P}}^G$).
$\iota _{\overline {P}}^G$).
Given two parabolic subgroups ![]() $\mathbb {P}_1\subset \mathbb {P}_2$ of
$\mathbb {P}_1\subset \mathbb {P}_2$ of ![]() $\mathbb {G}$ with Levi quotients
$\mathbb {G}$ with Levi quotients ![]() $\mathbb {M}_1$ and
$\mathbb {M}_1$ and ![]() $\mathbb {M}_2$, We write
$\mathbb {M}_2$, We write ![]() $\mathbb {P}_{12}$ for the image of
$\mathbb {P}_{12}$ for the image of ![]() $\mathbb {P}_1$ in
$\mathbb {P}_1$ in ![]() $\mathbb {M}_2$. Then we have natural isomorphisms
$\mathbb {M}_2$. Then we have natural isomorphisms
 \begin{equation} \begin{aligned} \iota_{P_{2}}^{G}\circ \iota_{P_{12}}^{M_2} & \longrightarrow \iota_{P_{1}}^{G},\\ \iota_{\overline{P}_{2}}^{G}\circ \iota_{\overline{P}_{12}}^{M_2} & \longrightarrow \iota_{\overline{P}_{1}}^{G} \end{aligned} \end{equation}
\begin{equation} \begin{aligned} \iota_{P_{2}}^{G}\circ \iota_{P_{12}}^{M_2} & \longrightarrow \iota_{P_{1}}^{G},\\ \iota_{\overline{P}_{2}}^{G}\circ \iota_{\overline{P}_{12}}^{M_2} & \longrightarrow \iota_{\overline{P}_{1}}^{G} \end{aligned} \end{equation}
of functors ![]() ${\bf D}({\rm Rep}_{[T_{M_1},1]}(M_1))\rightarrow {\bf D}({\rm Rep}_{[T,1]}(G))$.
${\bf D}({\rm Rep}_{[T_{M_1},1]}(M_1))\rightarrow {\bf D}({\rm Rep}_{[T,1]}(G))$.
Finally, recall that a Whittaker datum is a ![]() $G$-conjugacy class of tuples
$G$-conjugacy class of tuples ![]() $(\mathbb {B},\psi )$, where
$(\mathbb {B},\psi )$, where ![]() $\mathbb {B}\subset \mathbb {G}$ is a Borel subgroup and
$\mathbb {B}\subset \mathbb {G}$ is a Borel subgroup and ![]() $\psi :N\rightarrow C^\times$ is a generic character of
$\psi :N\rightarrow C^\times$ is a generic character of ![]() $N=\mathbb {N}(F)$, where
$N=\mathbb {N}(F)$, where ![]() $\mathbb {N}\subset \mathbb {B}$ is the unipotent radical. As above, we fix the choice of a Borel subgroup
$\mathbb {N}\subset \mathbb {B}$ is the unipotent radical. As above, we fix the choice of a Borel subgroup ![]() $\mathbb {B}$ and a maximal split torus
$\mathbb {B}$ and a maximal split torus ![]() $\mathbb {T}\subset \mathbb {G}$. For a parabolic
$\mathbb {T}\subset \mathbb {G}$. For a parabolic ![]() $\mathbb {P}\subset \mathbb {G}$ containing
$\mathbb {P}\subset \mathbb {G}$ containing ![]() $\mathbb {B}$ with Levi quotient
$\mathbb {B}$ with Levi quotient ![]() $\mathbb {M}$, we write
$\mathbb {M}$, we write ![]() $\psi _M:N_M\rightarrow C^\times$ for the restriction of
$\psi _M:N_M\rightarrow C^\times$ for the restriction of ![]() $\psi$ to the unipotent radical
$\psi$ to the unipotent radical ![]() $N_M\subset N$ of the Borel
$N_M\subset N$ of the Borel ![]() $B_M=B\cap M$ of
$B_M=B\cap M$ of ![]() $M$. Note that the
$M$. Note that the ![]() $M$-conjugacy class of
$M$-conjugacy class of ![]() $(B_M,\psi _M)$ does not depend on the choice of
$(B_M,\psi _M)$ does not depend on the choice of ![]() $\mathbb {M}\hookrightarrow \mathbb {G}$ (i.e. on the choice of
$\mathbb {M}\hookrightarrow \mathbb {G}$ (i.e. on the choice of ![]() $\mathbb {T}$).
$\mathbb {T}$).
We can describe the above categories of representations in terms of modules over Iwahori–Hecke algebras. In order to do so, let us fix a hyperspecial vertex in the apartment of the Bruhat–Tits building of ![]() $G$ defined by the maximal torus
$G$ defined by the maximal torus ![]() $\mathbb {T}$, that is, we fix
$\mathbb {T}$, that is, we fix ![]() $\mathcal {O}_F$-models of
$\mathcal {O}_F$-models of ![]() $(\mathbb {G},\mathbb {T})$. The choice of a Borel
$(\mathbb {G},\mathbb {T})$. The choice of a Borel ![]() $\mathbb {B}$ then defines an Iwahori subgroup
$\mathbb {B}$ then defines an Iwahori subgroup ![]() $I\subset G$. We write
$I\subset G$. We write ![]() ${\rm Rep}^I G$ for the category of smooth representations
${\rm Rep}^I G$ for the category of smooth representations ![]() $\pi$ of
$\pi$ of ![]() $G$ on
$G$ on ![]() $C$-vector spaces that are generated by their Iwahori fixed vectors
$C$-vector spaces that are generated by their Iwahori fixed vectors ![]() $\pi ^I$ and
$\pi ^I$ and ![]() ${\rm Rep}_{\rm fg}^I G\subset {\rm Rep}^I G$ for the full subcategory of representations that are finitely generated (as
${\rm Rep}_{\rm fg}^I G\subset {\rm Rep}^I G$ for the full subcategory of representations that are finitely generated (as ![]() $C[G]$-modules). It is well known that the category
$C[G]$-modules). It is well known that the category ![]() ${\rm Rep}^I G$ does not depend on the choice of
${\rm Rep}^I G$ does not depend on the choice of ![]() $I$ and agrees with the Bernstein block
$I$ and agrees with the Bernstein block ![]() ${\rm Rep}_{[T,1]}(G)$.
${\rm Rep}_{[T,1]}(G)$.
Let ![]() $\mathcal {H}_G=\mathcal {H}(G,I)={\rm End}_G(\text {c-ind}_I^G\mathbf {1}_I)$ denote the Iwahori–Hecke algebra. Then
$\mathcal {H}_G=\mathcal {H}(G,I)={\rm End}_G(\text {c-ind}_I^G\mathbf {1}_I)$ denote the Iwahori–Hecke algebra. Then
induces an equivalence of categories between ![]() ${\rm Rep}_{[T,1]}(G)={\rm Rep}^I G$ and the category
${\rm Rep}_{[T,1]}(G)={\rm Rep}^I G$ and the category ![]() $\mathcal {H}_G\text {-mod}$ of
$\mathcal {H}_G\text {-mod}$ of ![]() $\mathcal {H}_G$-modules. This equivalence identifies
$\mathcal {H}_G$-modules. This equivalence identifies ![]() ${\rm Rep}^I_{\rm fg} G$ and the full subcategory
${\rm Rep}^I_{\rm fg} G$ and the full subcategory ![]() $\mathcal {H}_G\text {-mod}_{\text {fg}}\subset \mathcal {H}_G\text {-mod}$ of finitely generated
$\mathcal {H}_G\text {-mod}_{\text {fg}}\subset \mathcal {H}_G\text {-mod}$ of finitely generated ![]() $\mathcal {H}_G$-modules. Moreover, it identifies the center
$\mathcal {H}_G$-modules. Moreover, it identifies the center ![]() $\mathfrak {Z}_G$ of
$\mathfrak {Z}_G$ of ![]() ${\rm Rep}_{[T,1]}(G)$ with the center of the Iwahori–Hecke algebra
${\rm Rep}_{[T,1]}(G)$ with the center of the Iwahori–Hecke algebra ![]() $\mathcal {H}_G$. Then we have an isomorphism
$\mathcal {H}_G$. Then we have an isomorphism
(see, for example, [Reference Haines, Kottwitz and PrasadHKP10, Lemma 2.3.1]), which is in fact independent of the choice of the Iwahori ![]() $I$.
$I$.
Given a representation ![]() $\pi \in {\rm Rep}^IG$ and a
$\pi \in {\rm Rep}^IG$ and a ![]() $\mathfrak {Z}_G$-module
$\mathfrak {Z}_G$-module ![]() $\rho$, we will sometimes (by abuse of notation) write
$\rho$, we will sometimes (by abuse of notation) write ![]() $\pi \otimes _{\mathfrak {Z}_G}\rho$ for the pre-image of the
$\pi \otimes _{\mathfrak {Z}_G}\rho$ for the pre-image of the ![]() $\mathcal {H}_G$-module
$\mathcal {H}_G$-module ![]() $\pi ^I\otimes _{\mathfrak {Z}_G}\rho$ under the equivalence of categories
$\pi ^I\otimes _{\mathfrak {Z}_G}\rho$ under the equivalence of categories ![]() ${\rm Rep}^I G\cong \mathcal {H}_G\text {-mod}$ (and similarly for corresponding derived functors).
${\rm Rep}^I G\cong \mathcal {H}_G\text {-mod}$ (and similarly for corresponding derived functors).
Remark 3.1 Note that if ![]() $\mathbb {G}=\mathbb {T}$ is a split torus, then
$\mathbb {G}=\mathbb {T}$ is a split torus, then ![]() $I=I_T=T^\circ$ is the unique maximal compact subgroup of
$I=I_T=T^\circ$ is the unique maximal compact subgroup of ![]() $T$ and we have canonical identifications
$T$ and we have canonical identifications
where the first isomorphism is given by ![]() $\mu \mapsto \mu (\varpi )$ for the choice of a uniformizer
$\mu \mapsto \mu (\varpi )$ for the choice of a uniformizer ![]() $\varpi$ of
$\varpi$ of ![]() $F$ (note that this isomorphism is independent of this choice). We often use this isomorphism to identify unramified characters and
$F$ (note that this isomorphism is independent of this choice). We often use this isomorphism to identify unramified characters and ![]() $\mathcal {H}_T$-modules.
$\mathcal {H}_T$-modules.
Let ![]() $\mathbb {P}\subset \mathbb {G}$ be a parabolic subgroup containing
$\mathbb {P}\subset \mathbb {G}$ be a parabolic subgroup containing ![]() $\mathbb {B}$ with Levi quotient
$\mathbb {B}$ with Levi quotient ![]() $\mathbb {M}$ and write
$\mathbb {M}$ and write ![]() $P=\mathbb {P}(F)$ and
$P=\mathbb {P}(F)$ and ![]() $M=\mathbb {M}(F)$. Set
$M=\mathbb {M}(F)$. Set ![]() $I_M=I_G\cap M$, which is an Iwahori subgroup of
$I_M=I_G\cap M$, which is an Iwahori subgroup of ![]() $M$; in particular, we have
$M$; in particular, we have ![]() ${\rm Rep}_{[T_M,1]}(M)={\rm Rep}^{I_M}M$. There is a canonical embedding
${\rm Rep}_{[T_M,1]}(M)={\rm Rep}^{I_M}M$. There is a canonical embedding ![]() $\mathcal {H}_M\hookrightarrow \mathcal {H}_G$ such that the diagrams
$\mathcal {H}_M\hookrightarrow \mathcal {H}_G$ such that the diagrams

commute. Note that this is equivalent to the commutativity of the diagram

Here ![]() $r^G_P(-)$ is the normalized Jacquet module which is the left adjoint functor to
$r^G_P(-)$ is the normalized Jacquet module which is the left adjoint functor to ![]() $\iota _P^G(-)$. It is also the right adjoint functor to
$\iota _P^G(-)$. It is also the right adjoint functor to ![]() $\iota _{\overline {P}}^G(-)$ by Bernstein's second adjointness theorem. By abuse of notation we will often write
$\iota _{\overline {P}}^G(-)$ by Bernstein's second adjointness theorem. By abuse of notation we will often write ![]() $\iota _{P}^G$ (respectively,
$\iota _{P}^G$ (respectively, ![]() $\iota _{\overline {P}}^G$) for the functors
$\iota _{\overline {P}}^G$) for the functors ![]() ${\rm Hom}_{\mathcal {H}_M}(\mathcal {H}_G,-)$ (respectively,
${\rm Hom}_{\mathcal {H}_M}(\mathcal {H}_G,-)$ (respectively, ![]() $\mathcal {H}_G\otimes _{\mathcal {H}_M}-$) on Hecke modules.
$\mathcal {H}_G\otimes _{\mathcal {H}_M}-$) on Hecke modules.
The embedding ![]() $\mathcal {H}_M\subset \mathcal {H}_G$ induces an embedding
$\mathcal {H}_M\subset \mathcal {H}_G$ induces an embedding ![]() $\mathfrak {Z}_G\subset \mathfrak {Z}_M$, where
$\mathfrak {Z}_G\subset \mathfrak {Z}_M$, where ![]() $\mathfrak {Z}_M$ is the center of
$\mathfrak {Z}_M$ is the center of ![]() ${\rm Rep}_{[T_M,1]}(M)$ which is identified with the center of
${\rm Rep}_{[T_M,1]}(M)$ which is identified with the center of ![]() $\mathcal {H}_M$, such that the canonical diagram
$\mathcal {H}_M$, such that the canonical diagram

commutes. We deduce that ![]() $\iota _P^G$ and
$\iota _P^G$ and ![]() $\iota _{\overline {P}}^G$ are
$\iota _{\overline {P}}^G$ are ![]() $\mathfrak {Z}_G$-linear. In particular, for a
$\mathfrak {Z}_G$-linear. In particular, for a ![]() $\mathfrak {Z}_G$-module
$\mathfrak {Z}_G$-module ![]() $\rho$ we obtain natural isomorphisms
$\rho$ we obtain natural isomorphisms
 \begin{equation} \begin{aligned} \iota_P^G(-\otimes_{\mathfrak{Z}_G}\rho) & \longrightarrow \iota_P^G(-)\otimes_{\mathfrak{Z}_G}\rho,\\ \iota_{\overline{P}}^G(-\otimes_{\mathfrak{Z}_G}\rho) & \longrightarrow \iota_{\overline{P}}^G(-) \otimes_{\mathfrak{Z}_G}\rho, \end{aligned} \end{equation}
\begin{equation} \begin{aligned} \iota_P^G(-\otimes_{\mathfrak{Z}_G}\rho) & \longrightarrow \iota_P^G(-)\otimes_{\mathfrak{Z}_G}\rho,\\ \iota_{\overline{P}}^G(-\otimes_{\mathfrak{Z}_G}\rho) & \longrightarrow \iota_{\overline{P}}^G(-) \otimes_{\mathfrak{Z}_G}\rho, \end{aligned} \end{equation}and similarly for the corresponding functors on the derived category.
3.2 The main conjecture
Using the notation introduced above, we state the following conjecture. Variants of the conjecture have been around in representation theory in recent years. A proof of the conjecture is announced in the work of Ben-Zvi et al. [Reference Ben-Zvi, Chen, Helm and NadlerBCHN20] and Zhu [Reference ZhuZhu20].
Conjecture 3.2 There exist the following data.
(i) For each
 $(\mathbb {G},\mathbb {B},\mathbb {T},\psi )$ consisting of a reductive group
$(\mathbb {G},\mathbb {B},\mathbb {T},\psi )$ consisting of a reductive group  $\mathbb {G}$, a Borel subgroup
$\mathbb {G}$, a Borel subgroup  $\mathbb {B}$, a split maximal torus
$\mathbb {B}$, a split maximal torus  $\mathbb {T}\subset \mathbb {B}$, and a (conjugacy class of a) generic character
$\mathbb {T}\subset \mathbb {B}$, and a (conjugacy class of a) generic character  $\psi :N\rightarrow C^\times$, there exists an exact and fully faithful
$\psi :N\rightarrow C^\times$, there exists an exact and fully faithful  $\mathfrak {Z}_G$-linear functor
$\mathfrak {Z}_G$-linear functor
 \[ R_G^\psi:{\bf D}^+({\rm Rep}_{[T,1]}(G))\longrightarrow {\bf D}^+_{\rm QCoh}([X_{\check G}/\check G]). \]
\[ R_G^\psi:{\bf D}^+({\rm Rep}_{[T,1]}(G))\longrightarrow {\bf D}^+_{\rm QCoh}([X_{\check G}/\check G]). \]
(ii) For
 $(\mathbb {G},\mathbb {B},\mathbb {T},\psi )$ as in (i) and each parabolic subgroup
$(\mathbb {G},\mathbb {B},\mathbb {T},\psi )$ as in (i) and each parabolic subgroup  $\mathbb {P}\subset \mathbb {G}$ containing
$\mathbb {P}\subset \mathbb {G}$ containing  $\mathbb {B}$, there exists a natural
$\mathbb {B}$, there exists a natural  $\mathfrak {Z}_{G}$-linear isomorphism
of functors
$\mathfrak {Z}_{G}$-linear isomorphism
of functors \[ \xi_{P}^{G}:R_{G}^\psi\circ \iota_{\overline{P}}^{G}\longrightarrow (R\beta_{\ast}\circ L\alpha^\ast)\circ R_{M}^{\psi_M} \]
\[ \xi_{P}^{G}:R_{G}^\psi\circ \iota_{\overline{P}}^{G}\longrightarrow (R\beta_{\ast}\circ L\alpha^\ast)\circ R_{M}^{\psi_M} \]
 ${\bf D}^+({\rm Rep}_{[T_M,1]}M)\rightarrow {\bf D}^+_{\rm QCoh}([X_{\check G}/\check G])$. Here
${\bf D}^+({\rm Rep}_{[T_M,1]}M)\rightarrow {\bf D}^+_{\rm QCoh}([X_{\check G}/\check G])$. Here  $\mathbb {M}$ is the Levi quotient of
$\mathbb {M}$ is the Levi quotient of  $\mathbb {P}$ and
are the morphisms on stacks induced by the natural maps
$\mathbb {P}$ and
are the morphisms on stacks induced by the natural maps \begin{align*} \alpha:[\mathbf{X}_{\check P}/\check P]&\longrightarrow[X_{\check M}/\check M],\\ \beta:[\mathbf{X}_{\check P}/\check P]&\longrightarrow[X_{\check G}/\check G] \end{align*}
\begin{align*} \alpha:[\mathbf{X}_{\check P}/\check P]&\longrightarrow[X_{\check M}/\check M],\\ \beta:[\mathbf{X}_{\check P}/\check P]&\longrightarrow[X_{\check G}/\check G] \end{align*}
 $\check P\rightarrow \check M$ and
$\check P\rightarrow \check M$ and  $\check P\rightarrow \check G$.
$\check P\rightarrow \check G$.
These data satisfy the following conditions.
(a) If
 $\mathbb {G}=\mathbb {T}$ is a split torus, then
$\mathbb {G}=\mathbb {T}$ is a split torus, then  $R_T=R_T^{\psi }$ is induced by the identification (3.4) and viewing a sheaf on
$R_T=R_T^{\psi }$ is induced by the identification (3.4) and viewing a sheaf on  $\check T$ as an
$\check T$ as an  $\check T$-equivariant sheaf with the trivial
$\check T$-equivariant sheaf with the trivial  $\check T$-action (note that
$\check T$-action (note that  $\check T$ acts trivially on
$\check T$ acts trivially on  $\check T=X_{\check T}$).
$\check T=X_{\check T}$).(b) Let
 $(\mathbb {G},\mathbb {B},\mathbb {T},\psi )$ be as in (i) and let
$(\mathbb {G},\mathbb {B},\mathbb {T},\psi )$ be as in (i) and let  $\mathbb {P}_1\subset \mathbb {P}_2\subset \mathbb {G}$ be parabolic subgroups containing
$\mathbb {P}_1\subset \mathbb {P}_2\subset \mathbb {G}$ be parabolic subgroups containing  $\mathbb {B}$ with Levi quotients
$\mathbb {B}$ with Levi quotients  $\mathbb {M}_1$ and
$\mathbb {M}_1$ and  $\mathbb {M}_2$. Let
$\mathbb {M}_2$. Let  $\mathbb {P}_{12}$ denote the image of
$\mathbb {P}_{12}$ denote the image of  $\mathbb {P}_1$ in
$\mathbb {P}_1$ in  $\mathbb {M}_2$. Then, with the notation from (2.6), the diagram
is a commutative diagram of functors
$\mathbb {M}_2$. Then, with the notation from (2.6), the diagram
is a commutative diagram of functors
 \[ {\bf D}^+({\rm Rep}_{[T_{M_1},1]}(M_1))\longrightarrow {\bf D}^+_{\rm QCoh}([X_{\check G}/\check G]). \]
\[ {\bf D}^+({\rm Rep}_{[T_{M_1},1]}(M_1))\longrightarrow {\bf D}^+_{\rm QCoh}([X_{\check G}/\check G]). \]
(c) For any
 $(\mathbb {G},\mathbb {B},\mathbb {T},\psi )$ as in (i), let
$(\mathbb {G},\mathbb {B},\mathbb {T},\psi )$ as in (i), let  $(\operatorname {c-ind}_N^G\psi )_{[T,1]}$ denote the projection of the compactly induced representation
$(\operatorname {c-ind}_N^G\psi )_{[T,1]}$ denote the projection of the compactly induced representation  $\operatorname {c-ind}_N^G\psi$ to
$\operatorname {c-ind}_N^G\psi$ to  ${\rm Rep}_{[T,1]}(G)$. Then
${\rm Rep}_{[T,1]}(G)$. Then
 \[ R_G^\psi((\operatorname{c-ind}_N^G\psi)_{[T,1]})\cong \mathcal{O}_{[X_{\check G}/\check G]}. \]
\[ R_G^\psi((\operatorname{c-ind}_N^G\psi)_{[T,1]})\cong \mathcal{O}_{[X_{\check G}/\check G]}. \]
Let us point out that the ![]() $\mathfrak {Z}_G$-linearity of the conjectured functor
$\mathfrak {Z}_G$-linearity of the conjectured functor ![]() $R_G^\psi$ implies that for each
$R_G^\psi$ implies that for each ![]() $\rho \in {\bf D}^+(\mathfrak {Z}_G\text {-}{\rm mod})$ there is a natural isomorphism
$\rho \in {\bf D}^+(\mathfrak {Z}_G\text {-}{\rm mod})$ there is a natural isomorphism
of functors ![]() ${\bf D}^+({\rm Rep}_{[T,1]}(G))\rightarrow {\bf D}^+_{\rm QCoh}([X_{\check G}/\check G])$ which is functorial in
${\bf D}^+({\rm Rep}_{[T,1]}(G))\rightarrow {\bf D}^+_{\rm QCoh}([X_{\check G}/\check G])$ which is functorial in ![]() $\rho$ (in the obvious sense). Moreover, given
$\rho$ (in the obvious sense). Moreover, given ![]() $\mathbb {P}\subset \mathbb {G}$ as in (ii), the
$\mathbb {P}\subset \mathbb {G}$ as in (ii), the ![]() $\mathfrak {Z}_{G}$-linearity of the natural isomorphism
$\mathfrak {Z}_{G}$-linearity of the natural isomorphism ![]() $\xi _{P}^{G}$ implies that the natural transformations
$\xi _{P}^{G}$ implies that the natural transformations ![]() $\psi _{M,\rho }$ and
$\psi _{M,\rho }$ and ![]() $\psi _{G,\rho }$ are compatible with parabolic induction. We do not spell this out explicitly in terms of commutative diagrams.
$\psi _{G,\rho }$ are compatible with parabolic induction. We do not spell this out explicitly in terms of commutative diagrams.
Remark 3.3 (a) We expect that the conjectured functor ![]() $R_G^\psi$ induces a functor
$R_G^\psi$ induces a functor
This would allow us to extend the functor to the full derived category ![]() ${\bf D}({\rm Rep}_{[T,1]}(G))$: as we have an equivalence of categories
${\bf D}({\rm Rep}_{[T,1]}(G))$: as we have an equivalence of categories ![]() ${\rm Rep}_{[T,1],{\rm fg}}(G)\cong \mathcal {H}_G\text {-mod}_{\text {fg}}$ and as
${\rm Rep}_{[T,1],{\rm fg}}(G)\cong \mathcal {H}_G\text {-mod}_{\text {fg}}$ and as ![]() $\mathcal {H}_G$ has finite global dimension (see [Reference BernsteinBer92, 4. Theorem 29]), the full derived category
$\mathcal {H}_G$ has finite global dimension (see [Reference BernsteinBer92, 4. Theorem 29]), the full derived category ![]() ${\bf D}({\rm Rep}_{[T,1]}(G))$ is the ind-completion of
${\bf D}({\rm Rep}_{[T,1]}(G))$ is the ind-completion of ![]() ${\bf D}^b({\rm Rep}_{[T,1],{\rm fg}}(G))$. Hence, the conjectured functor would extend to a fully faithful and exact functor
${\bf D}^b({\rm Rep}_{[T,1],{\rm fg}}(G))$. Hence, the conjectured functor would extend to a fully faithful and exact functor
where ![]() ${\rm IndCoh}([X_{\check G}/\check G])$ is the ind-completion of
${\rm IndCoh}([X_{\check G}/\check G])$ is the ind-completion of ![]() ${\bf D}^b_{\rm Coh}([X_{\check G}/\check G])$. Note that this category differs from
${\bf D}^b_{\rm Coh}([X_{\check G}/\check G])$. Note that this category differs from ![]() ${\bf D}_{\rm QCoh}([X_{\check G}/\check G])$, as
${\bf D}_{\rm QCoh}([X_{\check G}/\check G])$, as ![]() $X_{\check G}$ is singular. However, there is a canonical equivalence
$X_{\check G}$ is singular. However, there is a canonical equivalence
(see, for example, [Reference Drinfeld and GaitsgoryDG13, 3.2.4]). In particular, restricting to bounded-below objects, the conjecture that the (as yet hypothetical) functor ![]() $R_G^\psi$ is fully faithful does not depend on whether we consider it as a functor with values in
$R_G^\psi$ is fully faithful does not depend on whether we consider it as a functor with values in ![]() ${\rm IndCoh}^+([X_{\check G}/\check G])$ or with values in
${\rm IndCoh}^+([X_{\check G}/\check G])$ or with values in ![]() ${\bf D}^+_{\rm QCoh}([X_{\check G}/\check G])$. We hence arrive at a conjecture that parallels the formulation of the geometric Langlands program (see [Reference GaitsgoryGai15]). Also the conjectured compatibility with parabolic induction agrees with the compatibility with parabolic induction in [Reference GaitsgoryGai15]. See also the formulation given in [Reference ZhuZhu20, Conjecture 4.4.5].
${\bf D}^+_{\rm QCoh}([X_{\check G}/\check G])$. We hence arrive at a conjecture that parallels the formulation of the geometric Langlands program (see [Reference GaitsgoryGai15]). Also the conjectured compatibility with parabolic induction agrees with the compatibility with parabolic induction in [Reference GaitsgoryGai15]. See also the formulation given in [Reference ZhuZhu20, Conjecture 4.4.5].
(b) Recall that an L-parameter for ![]() $G$ that is trivial on inertia is a
$G$ that is trivial on inertia is a ![]() $\check G$-conjugacy class
$\check G$-conjugacy class ![]() $[\varphi,N]$ of
$[\varphi,N]$ of ![]() $(\varphi,N)\in X_{\check G}(C)$ with
$(\varphi,N)\in X_{\check G}(C)$ with ![]() $\varphi$ semi-simple. We write
$\varphi$ semi-simple. We write ![]() $S_{[\varphi,N]}=C_{[\varphi,N]}/C^\circ _{[\varphi,N]}$ for the quotient of the centralizer of
$S_{[\varphi,N]}=C_{[\varphi,N]}/C^\circ _{[\varphi,N]}$ for the quotient of the centralizer of ![]() $(\varphi,N)$ by its connected component of the identity. By the classification of Kazhdan and Lusztig [Reference Kazhdan and LusztigKL87, Theorem 7.12] the irreducible representations in
$(\varphi,N)$ by its connected component of the identity. By the classification of Kazhdan and Lusztig [Reference Kazhdan and LusztigKL87, Theorem 7.12] the irreducible representations in ![]() ${\rm Rep}^IG$ (and the simple objects in
${\rm Rep}^IG$ (and the simple objects in ![]() $\mathcal {H}_G\text {-mod}$) are in bijection with pairs
$\mathcal {H}_G\text {-mod}$) are in bijection with pairs ![]() $([\varphi,N],\rho )$, where
$([\varphi,N],\rho )$, where ![]() $[\varphi,N]$ is an L-parameter and
$[\varphi,N]$ is an L-parameter and ![]() $\rho$ runs through a certain set of irreducible representation of
$\rho$ runs through a certain set of irreducible representation of ![]() $S_{[\varphi,N]}$. This parametrization depends on an additional choice that corresponds to the choice of a Whittaker datum
$S_{[\varphi,N]}$. This parametrization depends on an additional choice that corresponds to the choice of a Whittaker datum ![]() $(\mathbb {B},\psi )$. More precisely, the classification in [Reference Kazhdan and LusztigKL87] (which in the case of
$(\mathbb {B},\psi )$. More precisely, the classification in [Reference Kazhdan and LusztigKL87] (which in the case of ![]() $\operatorname {GL}_n$ coincides with the Bernstein–Zelevinsky classification [Reference Bernstein and ZelevinskyBZ77]) associates to
$\operatorname {GL}_n$ coincides with the Bernstein–Zelevinsky classification [Reference Bernstein and ZelevinskyBZ77]) associates to ![]() $([\varphi,N],\rho )$ an indecomposable representation (respectively, Hecke module)
$([\varphi,N],\rho )$ an indecomposable representation (respectively, Hecke module) ![]() $\pi ^\psi _{[\varphi,N],\rho }$ which has a unique irreducible quotient. Conjecture 3.2 should have the following relation with this classification. For simplicity we only treat the case of regular semi-simple
$\pi ^\psi _{[\varphi,N],\rho }$ which has a unique irreducible quotient. Conjecture 3.2 should have the following relation with this classification. For simplicity we only treat the case of regular semi-simple ![]() $\varphi$; the general case seems to be much more involved (see remark (d) in § 4.7 for some discussion in the case of
$\varphi$; the general case seems to be much more involved (see remark (d) in § 4.7 for some discussion in the case of ![]() ${\rm GL}_n$)).
${\rm GL}_n$)).
Given ![]() $[\varphi,N]$, let us write
$[\varphi,N]$, let us write
for the ![]() $\check G$-orbit of
$\check G$-orbit of ![]() $(\varphi,N)$. Moreover, we denote by
$(\varphi,N)$. Moreover, we denote by
its Zariski closure. As we assume that ![]() $\varphi$ is regular semi-simple we can, given an irreducible representation
$\varphi$ is regular semi-simple we can, given an irreducible representation ![]() $\rho$ of
$\rho$ of ![]() $S_{[\varphi,N]}$ on a finite-dimensional
$S_{[\varphi,N]}$ on a finite-dimensional ![]() $C$-vector space, use
$C$-vector space, use ![]() $\rho$ to define a
$\rho$ to define a ![]() $\check G$-equivariant coherent sheaf
$\check G$-equivariant coherent sheaf
which hence defines a coherent sheaf ![]() $\mathcal {F}_{[\varphi,N],\rho }$ on the closed substack
$\mathcal {F}_{[\varphi,N],\rho }$ on the closed substack
We then expect that the conjectured functor ![]() $R_G$ has the property
$R_G$ has the property
If the L-parameter ![]() $[\varphi,N]$ is generic, there is a unique
$[\varphi,N]$ is generic, there is a unique ![]() $\psi$-generic representation
$\psi$-generic representation ![]() $\pi$ in the L-packet defined by
$\pi$ in the L-packet defined by ![]() $[\varphi,N]$. With the above notation this representation is the representation
$[\varphi,N]$. With the above notation this representation is the representation
Then the expected formula above specializes to
(c) We point out that the conjectured functor ![]() $R_G^\psi$ will not be essentially surjective. In fact this is already obvious in the case where
$R_G^\psi$ will not be essentially surjective. In fact this is already obvious in the case where ![]() $G=T$ a split torus. Here
$G=T$ a split torus. Here ![]() $R_T=R_T^\psi$ is the derived version of the functor
$R_T=R_T^\psi$ is the derived version of the functor
The morphism on the right-hand side is the embedding given by equipping a quasi-coherent sheaf with the trivial ![]() $\check T$-action. Obviously
$\check T$-action. Obviously ![]() $\check T$-equivariant sheaves with non-trivial
$\check T$-equivariant sheaves with non-trivial ![]() $\check T$-action are not in the essential image.
$\check T$-action are not in the essential image.
There is also a second obstruction for essential surjectivity for general ![]() $G$ (i.e.
$G$ (i.e. ![]() $G$ is not assumed to be a torus). Let
$G$ is not assumed to be a torus). Let ![]() $[\varphi,N]$ be an L-parameter such that
$[\varphi,N]$ be an L-parameter such that ![]() $\varphi$ is semi-simple but not regular semi-simple, and assume
$\varphi$ is semi-simple but not regular semi-simple, and assume ![]() $N=0$ for simplicity. Similarly to (b), we write
$N=0$ for simplicity. Similarly to (b), we write ![]() $X_{\check G,[\varphi,0]}\subset X_{\check G}$ for the closed subset of
$X_{\check G,[\varphi,0]}\subset X_{\check G}$ for the closed subset of ![]() $(\varphi ',0)$ such that
$(\varphi ',0)$ such that ![]() $\varphi '^{\rm ss}$ is in the
$\varphi '^{\rm ss}$ is in the ![]() $\check G$-orbit of
$\check G$-orbit of ![]() $\varphi ^{\rm ss}$. Then the structure sheaf of the closed substack
$\varphi ^{\rm ss}$. Then the structure sheaf of the closed substack
of pairs ![]() $(\varphi ',0)$ where
$(\varphi ',0)$ where ![]() $\varphi '$ is (pointwise) semi-simple should not be in the essential image of the functor
$\varphi '$ is (pointwise) semi-simple should not be in the essential image of the functor ![]() $R_G$. The same phenomenon should apply to all
$R_G$. The same phenomenon should apply to all ![]() $(\varphi,N)$ with
$(\varphi,N)$ with ![]() $\varphi$ not regular semi-simple (not only in the case
$\varphi$ not regular semi-simple (not only in the case ![]() $N=0$), but the definition of
$N=0$), but the definition of ![]() $X_{\check G,[\varphi,N]}$ is more involved in general (see remark (d) in § 4.7 for some details).
$X_{\check G,[\varphi,N]}$ is more involved in general (see remark (d) in § 4.7 for some details).
Following Fargues and Scholze [Reference Fargues and ScholzeFS21] and Zhu [Reference ZhuZhu20, 4.6], the failure of essential surjectivity should be fixed by replacing the category of smooth representations by a larger category.
(d) Finally, we point out that in the conjecture it is necessary to pass to derived categories. Heuristically this can be explained by the fact that flat morphisms on the representation theory side correspond to non-flat morphisms on the side of stacks: for example, ![]() $\mathcal {H}_G$ is flat over its center, whereas the canonical morphism
$\mathcal {H}_G$ is flat over its center, whereas the canonical morphism
is not flat (as it maps some irreducible components to proper closed subschemes of ![]() $\check T/W$). Moreover, we will see below that in the case of
$\check T/W$). Moreover, we will see below that in the case of ![]() ${\rm GL}_n(F)$ the trivial representation will be mapped to a complex concentrated in cohomological degree
${\rm GL}_n(F)$ the trivial representation will be mapped to a complex concentrated in cohomological degree ![]() $1-n$ (see Remark 4.43). Hence, without passing to derived categories, the functor cannot be fully faithful. The canonical t-structures on the source (or target) should correspond to an exotic t-structure on the other side. However, we have no idea how this t-structure could be described intrinsically. Moreover, the formulation of the conjecture needs the passage to derived schemes or derived stacks: as parabolic induction is transitive (in the sense that (3.3) is an isomorphism), the base change morphism (2.7) has to be an isomorphism as well. However, in the world of classical schemes the corresponding cartesian diagram is not Tor-independent in general.
$1-n$ (see Remark 4.43). Hence, without passing to derived categories, the functor cannot be fully faithful. The canonical t-structures on the source (or target) should correspond to an exotic t-structure on the other side. However, we have no idea how this t-structure could be described intrinsically. Moreover, the formulation of the conjecture needs the passage to derived schemes or derived stacks: as parabolic induction is transitive (in the sense that (3.3) is an isomorphism), the base change morphism (2.7) has to be an isomorphism as well. However, in the world of classical schemes the corresponding cartesian diagram is not Tor-independent in general.
3.3 A generalization of the conjecture
Conjecture 3.2 in fact is a special case of a more general conjecture about the category ![]() ${\rm Rep}(G)$, instead of the Bernstein block
${\rm Rep}(G)$, instead of the Bernstein block ![]() ${\rm Rep}_{[T,1]}(G)$. Let us describe this generalization. A similar generalization is conjectured by Zhu [Reference ZhuZhu20, Conjecture 4.5.1]. The generalization stated here can also be viewed as a special case of the main conjecture [Reference Fargues and ScholzeFS21, Conjecture I.10.2] of Fargues and Scholze.
${\rm Rep}_{[T,1]}(G)$. Let us describe this generalization. A similar generalization is conjectured by Zhu [Reference ZhuZhu20, Conjecture 4.5.1]. The generalization stated here can also be viewed as a special case of the main conjecture [Reference Fargues and ScholzeFS21, Conjecture I.10.2] of Fargues and Scholze.
We continue to assume that ![]() $\mathbb {G}$ is a split reductive group with dual group
$\mathbb {G}$ is a split reductive group with dual group ![]() $\check G$. Let us write
$\check G$. Let us write ![]() $W_F$ for the Weil group of
$W_F$ for the Weil group of ![]() $F$ and
$F$ and ![]() $I_F\subset W_F$ for the inertia group. We define the space of
$I_F\subset W_F$ for the inertia group. We define the space of ![]() $\check G$-valued Weil–Deligne representations to be the scheme
$\check G$-valued Weil–Deligne representations to be the scheme ![]() $X_{\check G}^{\rm WD}$ representing the functor
$X_{\check G}^{\rm WD}$ representing the functor
on ![]() $C$-algebras
$C$-algebras ![]() $R$. Here
$R$. Here ![]() $\|-\|:W_F\rightarrow \mathbb {Z}$ is the usual projection. It is easy to see that
$\|-\|:W_F\rightarrow \mathbb {Z}$ is the usual projection. It is easy to see that ![]() $X_{\check G}^{\rm WD}$ is an infinite disjoint union of affine schemes and is equipped with a
$X_{\check G}^{\rm WD}$ is an infinite disjoint union of affine schemes and is equipped with a ![]() $\check G$-action via conjugation on
$\check G$-action via conjugation on ![]() $\rho$ and via the adjoint action on
$\rho$ and via the adjoint action on ![]() $N$. The space of Weil–Deligne representations
$N$. The space of Weil–Deligne representations ![]() $X_{\check G}^{\rm WD}$ in fact agrees with the fiber over
$X_{\check G}^{\rm WD}$ in fact agrees with the fiber over ![]() $C$ of the moduli space of L-parameters
$C$ of the moduli space of L-parameters ![]() $\underline {Z}^1(W_F^\circ,\check G)$ studied in work of Dat et al. [Reference Dat, Helm, Kurinczuk and MossDHKM20] and is defined and studied as well in [Reference ZhuZhu20, 3.1].
$\underline {Z}^1(W_F^\circ,\check G)$ studied in work of Dat et al. [Reference Dat, Helm, Kurinczuk and MossDHKM20] and is defined and studied as well in [Reference ZhuZhu20, 3.1].
Similarly, for every parabolic subgroup ![]() $\check P\subset \check G$ we can define the scheme
$\check P\subset \check G$ we can define the scheme ![]() $X_{\check P}^{\rm WD}$ and the derived scheme
$X_{\check P}^{\rm WD}$ and the derived scheme ![]() ${\bf X}_{\check P}^{\rm WD}$ that come equipped with
${\bf X}_{\check P}^{\rm WD}$ that come equipped with ![]() $\check P$-actions.
$\check P$-actions.
The inclusion ![]() $\check P\hookrightarrow \check G$ and the projection
$\check P\hookrightarrow \check G$ and the projection ![]() $\check P\rightarrow \check M$ onto the Levi quotient
$\check P\rightarrow \check M$ onto the Levi quotient ![]() $\check M$ of
$\check M$ of ![]() $\check P$ induce morphisms
$\check P$ induce morphisms
 \begin{equation} \begin{aligned} \beta_{\check P}^{\rm WD}:[{\bf X}_{\check P}^{\rm WD}/\check P] & \longrightarrow [X_{\check G}^{\rm WD}/\check G],\\ \alpha_{\check P}^{\rm WD}:[{\bf X}_{\check P}^{\rm WD}/\check P] & \longrightarrow [X_{\check M}^{\rm WD}/\check M] \end{aligned} \end{equation}
\begin{equation} \begin{aligned} \beta_{\check P}^{\rm WD}:[{\bf X}_{\check P}^{\rm WD}/\check P] & \longrightarrow [X_{\check G}^{\rm WD}/\check G],\\ \alpha_{\check P}^{\rm WD}:[{\bf X}_{\check P}^{\rm WD}/\check P] & \longrightarrow [X_{\check M}^{\rm WD}/\check M] \end{aligned} \end{equation}
of the respective stack quotients. Moreover, we will write ![]() $X_{\check G}^{\rm WD}/\hspace {-0.1cm}/\check G$ for the GIT quotient of
$X_{\check G}^{\rm WD}/\hspace {-0.1cm}/\check G$ for the GIT quotient of ![]() $X_{\check G}^{\rm WD}$ by the
$X_{\check G}^{\rm WD}$ by the ![]() $\check G$-action. As in the case of the space of
$\check G$-action. As in the case of the space of ![]() $(\varphi,N)$-modules
$(\varphi,N)$-modules ![]() $X_{\check G}$, it is easy to show that
$X_{\check G}$, it is easy to show that ![]() $\beta _{\check P}^{\rm WD}$ is proper. The following summarizes properties of the spaces just introduced (which are proved using methods similar to those in § 2).
$\beta _{\check P}^{\rm WD}$ is proper. The following summarizes properties of the spaces just introduced (which are proved using methods similar to those in § 2).
Let ![]() $\check P\subset \check G$ be a parabolic subgroup with Levi quotient
$\check P\subset \check G$ be a parabolic subgroup with Levi quotient ![]() $\check M$.
$\check M$.
(i) The space
 $X_{\check G}^{\rm WD}$ is reduced and a local complete intersection. (This follows from [Reference Dat, Helm, Kurinczuk and MossDHKM20, Theorem 4.1]. See also [Reference ZhuZhu20, Proposition 3.1.6].)
$X_{\check G}^{\rm WD}$ is reduced and a local complete intersection. (This follows from [Reference Dat, Helm, Kurinczuk and MossDHKM20, Theorem 4.1]. See also [Reference ZhuZhu20, Proposition 3.1.6].)(ii) The morphism
 $\alpha _{\check P}^{\rm WD}:[{\bf X}_{\check P}^{\rm WD}/\check P]\rightarrow [X_{\check M}^{\rm WD}/\check M]$ has finite Tor dimension. (This follows from [Reference ZhuZhu20, Lemma 3.3.1].)
$\alpha _{\check P}^{\rm WD}:[{\bf X}_{\check P}^{\rm WD}/\check P]\rightarrow [X_{\check M}^{\rm WD}/\check M]$ has finite Tor dimension. (This follows from [Reference ZhuZhu20, Lemma 3.3.1].)(iii) There is a morphism
 $X_{\check M}^{\rm WD}/\hspace {-.1cm}/\check M\rightarrow X_{\check G}^{\rm WD}/\hspace {-.1cm}/\check G$ making the diagram
commutative. (This is the commutative diagram [Reference ZhuZhu20, (3.10)]. The morphism can easily be constructed using the morphism
$X_{\check M}^{\rm WD}/\hspace {-.1cm}/\check M\rightarrow X_{\check G}^{\rm WD}/\hspace {-.1cm}/\check G$ making the diagram
commutative. (This is the commutative diagram [Reference ZhuZhu20, (3.10)]. The morphism can easily be constructed using the morphism
 $X_{\check M}^{\rm WD}\rightarrow \mathbf {X}^{\rm WD}_{\check P}$ induced by the choice of a splitting of
$X_{\check M}^{\rm WD}\rightarrow \mathbf {X}^{\rm WD}_{\check P}$ induced by the choice of a splitting of  $\check P\rightarrow \check M$.)
$\check P\rightarrow \check M$.)
Remark 3.4 In the case of the space of ![]() $(\varphi,N)$-modules
$(\varphi,N)$-modules ![]() $X_{\check G}$ all these properties have been verified in § 2. In relation to (iii) we remark that the morphism
$X_{\check G}$ all these properties have been verified in § 2. In relation to (iii) we remark that the morphism
is just the morphism ![]() $\bar \chi$ from (3.1), that is, the GIT quotient
$\bar \chi$ from (3.1), that is, the GIT quotient ![]() $X_{\check G}/\hspace {-.1cm}/\check G$ agrees with the adjoint quotient
$X_{\check G}/\hspace {-.1cm}/\check G$ agrees with the adjoint quotient ![]() $\check G/\hspace {-.1cm}/\check G$. This can be seen as follows. The morphism
$\check G/\hspace {-.1cm}/\check G$. This can be seen as follows. The morphism ![]() $\varphi \mapsto (\varphi,0)$ defines a closed embedding
$\varphi \mapsto (\varphi,0)$ defines a closed embedding ![]() $\check G\hookrightarrow X_{\check G}$ which is the inclusion of an irreducible component. As
$\check G\hookrightarrow X_{\check G}$ which is the inclusion of an irreducible component. As ![]() $\check G$ is reductive and
$\check G$ is reductive and ![]() $C$ has characteristic zero, the category of
$C$ has characteristic zero, the category of ![]() $\check G$-representations is semi-simple and we obtain a closed embedding
$\check G$-representations is semi-simple and we obtain a closed embedding
As source and target are reduced (as ![]() $\check G$ and
$\check G$ and ![]() $X_{\check G}$ are) it is enough to show that the morphism is bijective. This comes down to proving that for
$X_{\check G}$ are) it is enough to show that the morphism is bijective. This comes down to proving that for ![]() $(\varphi,N)\in X_{\check G}(k)$, for an algebraically closed field
$(\varphi,N)\in X_{\check G}(k)$, for an algebraically closed field ![]() $k$, there exists
$k$, there exists ![]() $\varphi '\in \check G(k)$ such that
$\varphi '\in \check G(k)$ such that
By (the proof of) Lemma 2.5 we may assume that ![]() $\varphi \in \check B$ and
$\varphi \in \check B$ and ![]() $N\in \operatorname {Lie}\check B$ for some Borel
$N\in \operatorname {Lie}\check B$ for some Borel ![]() $\check B\subset \check G$. Let
$\check B\subset \check G$. Let ![]() $\mathbb {G}_m$ act on
$\mathbb {G}_m$ act on ![]() $X_{\check G}$ by the sum of the positive roots. Then the closure of
$X_{\check G}$ by the sum of the positive roots. Then the closure of ![]() $\mathbb {G}_m\cdot (\varphi,N)$ contains in addition the point
$\mathbb {G}_m\cdot (\varphi,N)$ contains in addition the point ![]() $(\varphi ',0)$ for some
$(\varphi ',0)$ for some ![]() $\varphi '\in \check G$ such that
$\varphi '\in \check G$ such that ![]() $\varphi$ and
$\varphi$ and ![]() $\varphi '$ have the same image in the adjoint quotient
$\varphi '$ have the same image in the adjoint quotient ![]() $\check G/\hspace {-.1cm}/\check G$.
$\check G/\hspace {-.1cm}/\check G$.
Let us write ![]() $\mathfrak {Z}(G)$ for the Bernstein center of the category
$\mathfrak {Z}(G)$ for the Bernstein center of the category ![]() ${\rm Rep}(G)$. Given a Bernstein component
${\rm Rep}(G)$. Given a Bernstein component ![]() $\Omega$ of
$\Omega$ of ![]() ${\rm Rep}(G)$, we denote its center by
${\rm Rep}(G)$, we denote its center by ![]() $\mathfrak {Z}_\Omega (G)$. Moreover, we denote by
$\mathfrak {Z}_\Omega (G)$. Moreover, we denote by
the ring of functions on the GIT quotient ![]() $X_{\check G}^{\rm WD}/\hspace {-.1cm}/\check G$. If
$X_{\check G}^{\rm WD}/\hspace {-.1cm}/\check G$. If ![]() $X\subset X_{\check G}^{\rm WD}$ is a connected component, we write
$X\subset X_{\check G}^{\rm WD}$ is a connected component, we write ![]() $\mathcal {Z}_X(\check G)$ for the ring of functions on the GIT quotient
$\mathcal {Z}_X(\check G)$ for the ring of functions on the GIT quotient ![]() $X/\hspace {-.1cm}/\check G$.
$X/\hspace {-.1cm}/\check G$.
Remark 3.5 If ![]() $\mathbb {G}=\mathbb {T}$ is a split torus, then the isomorphism
$\mathbb {G}=\mathbb {T}$ is a split torus, then the isomorphism ![]() $F^\times \rightarrow W_F^{\rm ab}$ of local class field theory identifies
$F^\times \rightarrow W_F^{\rm ab}$ of local class field theory identifies ![]() $X_{\check T}^{\rm WD}$ with the scheme representing the functor
$X_{\check T}^{\rm WD}$ with the scheme representing the functor
on the category of ![]() $C$-algebras. In particular, the scheme
$C$-algebras. In particular, the scheme ![]() $X_{\check T}^{\rm WD}$ decomposes into a disjoint union of copies of
$X_{\check T}^{\rm WD}$ decomposes into a disjoint union of copies of ![]() $\check T$ indexed by the smooth characters
$\check T$ indexed by the smooth characters ![]() $\mathcal {O}_F^{\times }\rightarrow \check T(C)$. This decomposition induces an equivalence of categories
$\mathcal {O}_F^{\times }\rightarrow \check T(C)$. This decomposition induces an equivalence of categories
We state a generalization of Conjecture 3.2.
Conjecture 3.6 There exist the following data.
(i) For each
 $(\mathbb {G},\mathbb {B},\mathbb {T},\psi )$ consisting of a reductive group
$(\mathbb {G},\mathbb {B},\mathbb {T},\psi )$ consisting of a reductive group  $\mathbb {G}$, a Borel subgroup
$\mathbb {G}$, a Borel subgroup  $\mathbb {B}$, a split maximal torus
$\mathbb {B}$, a split maximal torus  $\mathbb {T}\subset \mathbb {B}$, and a (conjugacy class of a) generic character
$\mathbb {T}\subset \mathbb {B}$, and a (conjugacy class of a) generic character  $\psi :N\rightarrow C^\times$, there exists an exact and fully faithful functor
$\psi :N\rightarrow C^\times$, there exists an exact and fully faithful functor
 \[ \mathcal{R}_G^\psi:{\bf D}^+({\rm Rep}(G))\longrightarrow {\bf D}^+_{\rm QCoh}([X^{\rm WD}_{\check G}/\check G]). \]
\[ \mathcal{R}_G^\psi:{\bf D}^+({\rm Rep}(G))\longrightarrow {\bf D}^+_{\rm QCoh}([X^{\rm WD}_{\check G}/\check G]). \]
(ii) For
 $(\mathbb {G},\mathbb {B},\mathbb {T},\psi )$ as in (i) and each parabolic subgroup
$(\mathbb {G},\mathbb {B},\mathbb {T},\psi )$ as in (i) and each parabolic subgroup  $\mathbb {P}\subset \mathbb {G}$ containing
$\mathbb {P}\subset \mathbb {G}$ containing  $\mathbb {B}$, there exists a natural isomorphism
of functors
$\mathbb {B}$, there exists a natural isomorphism
of functors \[ \xi_{P}^{G}:\mathcal{R}_{G}^\psi\circ \iota_{\overline{P}}^{G}\longrightarrow (R\beta^{\rm WD}_{\check P,\ast}\circ L\alpha_{\check P}^{{\rm WD},\ast})\circ \mathcal{R}_{M}^{\psi_M} \]
\[ \xi_{P}^{G}:\mathcal{R}_{G}^\psi\circ \iota_{\overline{P}}^{G}\longrightarrow (R\beta^{\rm WD}_{\check P,\ast}\circ L\alpha_{\check P}^{{\rm WD},\ast})\circ \mathcal{R}_{M}^{\psi_M} \]
 ${\bf D}^+({\rm Rep}(M))\rightarrow {\bf D}^+_{\rm QCoh}([X^{\rm WD}_{\check G}/\check G])$. Here
${\bf D}^+({\rm Rep}(M))\rightarrow {\bf D}^+_{\rm QCoh}([X^{\rm WD}_{\check G}/\check G])$. Here  $\mathbb {M}$ is the Levi quotient of
$\mathbb {M}$ is the Levi quotient of  $\mathbb {P}$ and
$\mathbb {P}$ and  $\alpha _{\check P}^{\rm WD}$ and
$\alpha _{\check P}^{\rm WD}$ and  $\beta _{\check P}^{\rm WD}$ are the morphisms defined in (3.8).
$\beta _{\check P}^{\rm WD}$ are the morphisms defined in (3.8).
These data satisfy the following conditions.
(a) If
 $\mathbb {G}=\mathbb {T}$ is a split torus, then
$\mathbb {G}=\mathbb {T}$ is a split torus, then  $\mathcal {R}_T=\mathcal {R}_T^{\psi }$ is induced by the equivalence (3.9) given by local class field theory.
$\mathcal {R}_T=\mathcal {R}_T^{\psi }$ is induced by the equivalence (3.9) given by local class field theory.(b) Let
 $(\mathbb {G},\mathbb {B},\mathbb {T},\psi )$ be as in (i). The morphism
$(\mathbb {G},\mathbb {B},\mathbb {T},\psi )$ be as in (i). The morphism  $\mathcal {Z}(\check G)\rightarrow \mathfrak {Z}(G)$ defined by full faithfulness of
$\mathcal {Z}(\check G)\rightarrow \mathfrak {Z}(G)$ defined by full faithfulness of  $\mathcal {R}_G^\psi$ is independent of the choice of
$\mathcal {R}_G^\psi$ is independent of the choice of  $\psi$ and induces a surjection
$\psi$ and induces a surjection
 \[
\omega_G:\left\{\begin{array}{@{}c@{}} \text{Bernstein
components}\\ \text{of}\ {\rm Rep} (G)
\end{array}\right\}\longrightarrow\left\{\begin{array}{@{}c@{}}
\text{connected components}\\ \text{of}\ X_{\check G}^{\rm
WD} \end{array}\right\}. \]
\[
\omega_G:\left\{\begin{array}{@{}c@{}} \text{Bernstein
components}\\ \text{of}\ {\rm Rep} (G)
\end{array}\right\}\longrightarrow\left\{\begin{array}{@{}c@{}}
\text{connected components}\\ \text{of}\ X_{\check G}^{\rm
WD} \end{array}\right\}. \]
(c) Let
 $(\mathbb {G},\mathbb {B},\mathbb {T},\psi )$ and
$(\mathbb {G},\mathbb {B},\mathbb {T},\psi )$ and  $\mathbb {P}$ be as in (ii). Then the natural isomorphism
$\mathbb {P}$ be as in (ii). Then the natural isomorphism  $\xi _P^G$ is
$\xi _P^G$ is  $\mathcal {Z}(\check G)$-linear for the
$\mathcal {Z}(\check G)$-linear for the  $\mathcal {Z}(\check G)$-linear structure on
$\mathcal {Z}(\check G)$-linear structure on  ${\rm Rep}(M)$ defined by the morphism
that is given by the composition of the morphism
${\rm Rep}(M)$ defined by the morphism
that is given by the composition of the morphism \[ \mathcal{Z}(\check G)\longrightarrow\mathcal{Z}(\check M)\longrightarrow \mathfrak{Z}(M) \]
\[ \mathcal{Z}(\check G)\longrightarrow\mathcal{Z}(\check M)\longrightarrow \mathfrak{Z}(M) \]
 $\mathcal {Z}(\check G)\rightarrow \mathcal {Z}(\check M)$ (which is induced by
$\mathcal {Z}(\check G)\rightarrow \mathcal {Z}(\check M)$ (which is induced by  $X_{\check M}^{\rm WD}/\hspace {-.1cm}/\check M\rightarrow X_{\check G}^{\rm WD}/\hspace {-.1cm}/\check G$) with the morphism
$X_{\check M}^{\rm WD}/\hspace {-.1cm}/\check M\rightarrow X_{\check G}^{\rm WD}/\hspace {-.1cm}/\check G$) with the morphism  $\mathcal {Z}(\check M)\rightarrow \mathfrak {Z}(M)$ of (b).
$\mathcal {Z}(\check M)\rightarrow \mathfrak {Z}(M)$ of (b).(d) Let
 $(\mathbb {G},\mathbb {B},\mathbb {T},\psi )$ as in (i) and let
$(\mathbb {G},\mathbb {B},\mathbb {T},\psi )$ as in (i) and let  $\mathbb {P}_1\subset \mathbb {P}_2\subset \mathbb {G}$ be parabolic subgroups containing
$\mathbb {P}_1\subset \mathbb {P}_2\subset \mathbb {G}$ be parabolic subgroups containing  $\mathbb {B}$ with Levi quotients
$\mathbb {B}$ with Levi quotients  $\mathbb {M}_1$ and
$\mathbb {M}_1$ and  $\mathbb {M}_2$. Let
$\mathbb {M}_2$. Let  $\mathbb {P}_{12}$ denote the image of
$\mathbb {P}_{12}$ denote the image of  $\mathbb {P}_1$ in
$\mathbb {P}_1$ in  $\mathbb {M}_2$. Then the diagram
is a commutative diagram of functors
$\mathbb {M}_2$. Then the diagram
is a commutative diagram of functors Here
Here \[ {\bf D}^+({\rm Rep}(M_1))\longrightarrow {\bf D}^+_{\rm QCoh}([X^{\rm WD}_{\check G}/\check G]). \]
\[ {\bf D}^+({\rm Rep}(M_1))\longrightarrow {\bf D}^+_{\rm QCoh}([X^{\rm WD}_{\check G}/\check G]). \]
 $(\ast )$ is the natural isomorphism given by transitivity of parabolic induction and
$(\ast )$ is the natural isomorphism given by transitivity of parabolic induction and  $(\ast \ast )$ is a base change isomorphism defined by the analogous diagram as in (2.6).
$(\ast \ast )$ is a base change isomorphism defined by the analogous diagram as in (2.6).(e) For
 $(\mathbb {G},\mathbb {B},\mathbb {T},\psi )$ as in (i) there is an isomorphism
$(\mathbb {G},\mathbb {B},\mathbb {T},\psi )$ as in (i) there is an isomorphism
 \[ \mathcal{R}_G^\psi(\operatorname{c-ind}_N^G\psi)\cong \mathcal{O}_{[X^{\rm WD}_{\check G}/\check G]}. \]
\[ \mathcal{R}_G^\psi(\operatorname{c-ind}_N^G\psi)\cong \mathcal{O}_{[X^{\rm WD}_{\check G}/\check G]}. \]
Remark 3.7 (i) It should be possible to construct the expected morphism
of (b) in the conjecture, without referring to the conjectured functor ![]() $\mathcal {R}_G^\psi$. In the case of
$\mathcal {R}_G^\psi$. In the case of ![]() ${\rm GL}_n$ a result like this has been established by Helm and Moss [Reference Helm and MossHM18] (even with
${\rm GL}_n$ a result like this has been established by Helm and Moss [Reference Helm and MossHM18] (even with ![]() $\mathbb {Z}_{\ell }$-coefficients). More generally, Fargues and Scholze [Reference Fargues and ScholzeFS21, Proposition I.9.3] give a construction of such a morphism using the spectral action constructed in [Reference Fargues and ScholzeFS21]. While the morphism is an isomorphism in the
$\mathbb {Z}_{\ell }$-coefficients). More generally, Fargues and Scholze [Reference Fargues and ScholzeFS21, Proposition I.9.3] give a construction of such a morphism using the spectral action constructed in [Reference Fargues and ScholzeFS21]. While the morphism is an isomorphism in the ![]() ${\rm GL}_n$ case of [Reference Helm and MossHM18], this is not true in the general case.
${\rm GL}_n$ case of [Reference Helm and MossHM18], this is not true in the general case.
(ii) In fact ![]() $\mathcal {Z}(\check G)$ coincides with the stable Bernstein center as defined by Haines in [Reference Haines, Diamond, Kassaei and KimHai14, 5.3]. This is a consequence of [Reference Dat, Helm, Kurinczuk and MossDHKM20, Theorem 6.10]. With this identification the morphism
$\mathcal {Z}(\check G)$ coincides with the stable Bernstein center as defined by Haines in [Reference Haines, Diamond, Kassaei and KimHai14, 5.3]. This is a consequence of [Reference Dat, Helm, Kurinczuk and MossDHKM20, Theorem 6.10]. With this identification the morphism ![]() $\mathcal {Z}(\check G)\rightarrow \mathfrak {Z}(G)$ of (b) in the conjecture should coincide with the morphism constructed in [Reference Haines, Diamond, Kassaei and KimHai14, Proposition 5.5.1] assuming the local Langlands correspondence.
$\mathcal {Z}(\check G)\rightarrow \mathfrak {Z}(G)$ of (b) in the conjecture should coincide with the morphism constructed in [Reference Haines, Diamond, Kassaei and KimHai14, Proposition 5.5.1] assuming the local Langlands correspondence.
Let us point out that the morphism ![]() $\omega _G$ from (b) cannot be expected to be a bijection in general, as, for a given Whittaker datum
$\omega _G$ from (b) cannot be expected to be a bijection in general, as, for a given Whittaker datum ![]() $\psi$, not every Bernstein component
$\psi$, not every Bernstein component ![]() $\Omega$ is
$\Omega$ is ![]() $\psi$-genericFootnote 6 in the sense of [Reference Bushnell and HenniartBH03, 4.3] (note that the notions of being
$\psi$-genericFootnote 6 in the sense of [Reference Bushnell and HenniartBH03, 4.3] (note that the notions of being ![]() $\psi$-generic and being simply
$\psi$-generic and being simply ![]() $\psi$-generic of [Reference Bushnell and HenniartBH03] agree by [Reference Bushnell and HenniartBH03, Example 4.5(1)], as
$\psi$-generic of [Reference Bushnell and HenniartBH03] agree by [Reference Bushnell and HenniartBH03, Example 4.5(1)], as ![]() $\mathbb {G}$ is assumed to be (quasi-)split). More precisely, Conjecture 3.6 predicts that the restriction of
$\mathbb {G}$ is assumed to be (quasi-)split). More precisely, Conjecture 3.6 predicts that the restriction of ![]() $\omega _G$ induces a bijection
$\omega _G$ induces a bijection
and that for a ![]() $\psi$-generic Bernstein component
$\psi$-generic Bernstein component ![]() $\Omega$ the induced morphism
$\Omega$ the induced morphism
is an isomorphism. Indeed, combining Corollary 4.2 and Theorem 4.3 of [Reference Bushnell and HenniartBH03], we deduce that the ![]() $\psi$-generic components are precisely those components
$\psi$-generic components are precisely those components ![]() $\Omega$ such that
$\Omega$ such that ![]() $(\operatorname {c-ind}_N^G\psi )_\Omega \neq 0$. Moreover, morphism (3.10) fits in the commutative diagram
$(\operatorname {c-ind}_N^G\psi )_\Omega \neq 0$. Moreover, morphism (3.10) fits in the commutative diagram

where ![]() $X_{\check G,\Omega }^{\rm WD}\subset X_{\check G}^{\rm WD}$ denotes the connected component defined by
$X_{\check G,\Omega }^{\rm WD}\subset X_{\check G}^{\rm WD}$ denotes the connected component defined by ![]() $\omega _G(\Omega )$. Here the upper horizontal arrow is an isomorphism by (e) and full faithfulness in the conjecture, the right vertical arrow is an isomorphism by definition and the left vertical arrow is an isomorphism by [Reference Bushnell and HenniartBH03, 4.3. Theorem].
$\omega _G(\Omega )$. Here the upper horizontal arrow is an isomorphism by (e) and full faithfulness in the conjecture, the right vertical arrow is an isomorphism by definition and the left vertical arrow is an isomorphism by [Reference Bushnell and HenniartBH03, 4.3. Theorem].
Remark 3.8 Conjecture 3.2 is concerned with the principal component ![]() ${\rm Rep}_{[T,1]}(G)$. This Bernstein component is
${\rm Rep}_{[T,1]}(G)$. This Bernstein component is ![]() $\psi$-generic for any choice of
$\psi$-generic for any choice of ![]() $\psi$.
$\psi$.
Remark 3.9 In the case of ![]() $\mathbb {G}={\rm GL}_n$ there is (up to conjugation) a unique choice of
$\mathbb {G}={\rm GL}_n$ there is (up to conjugation) a unique choice of ![]() $(\mathbb {B},\psi )$ and every Bernstein component of
$(\mathbb {B},\psi )$ and every Bernstein component of ![]() ${\rm Rep}({\rm GL}_n(F))$ is
${\rm Rep}({\rm GL}_n(F))$ is ![]() $\psi$-generic (see, for example, [Reference Bushnell and HenniartBH03, 4.5, Examples (2)]). Moreover, in this case one can show that
$\psi$-generic (see, for example, [Reference Bushnell and HenniartBH03, 4.5, Examples (2)]). Moreover, in this case one can show that ![]() $X_{\check G}^{\rm WD}$ decomposes into a disjoint union
$X_{\check G}^{\rm WD}$ decomposes into a disjoint union
where ![]() $\underline {n}=(n_{[\tau ]})$ is a tuple of non-negative integers
$\underline {n}=(n_{[\tau ]})$ is a tuple of non-negative integers ![]() $n_{[\tau ]}$ indexed by the
$n_{[\tau ]}$ indexed by the ![]() $W_F$-conjugacy classes
$W_F$-conjugacy classes ![]() $[\tau ]$ of irreducible
$[\tau ]$ of irreducible ![]() $I_F$-representations
$I_F$-representations ![]() $\tau :I_F\rightarrow {\rm GL}_{d_\tau }(C)$ such that
$\tau :I_F\rightarrow {\rm GL}_{d_\tau }(C)$ such that
Here ![]() $W_\tau \subset W_F$ is the
$W_\tau \subset W_F$ is the ![]() $W_F$-stabilizer of a representative
$W_F$-stabilizer of a representative ![]() $\tau$ of
$\tau$ of ![]() $[\tau ]$. Moreover, each
$[\tau ]$. Moreover, each ![]() $X_{\underline {n}}$ is connected and decomposes into a product where each factor is a space of
$X_{\underline {n}}$ is connected and decomposes into a product where each factor is a space of ![]() $(\varphi,N)$-modules for a finite extension
$(\varphi,N)$-modules for a finite extension ![]() $F'$ of
$F'$ of ![]() $F$. On the other hand, the local Langlands correspondence for
$F$. On the other hand, the local Langlands correspondence for ![]() ${\rm GL}_n(F)$ induces a bijection
${\rm GL}_n(F)$ induces a bijection
 \[
\left\{\begin{array}{@{}c@{}} W_F\text{-conjugacy classes
of}\\ \text{irreducible smooth representations}\\
\tau:I_F\rightarrow {\rm GL}_m(C),\quad m\geq 1
\end{array}\right\}\longleftrightarrow
\left\{\begin{array}{@{}c@{}} \text{equivalence classes
of}\\ \text{cuspidal representations}\\ {\rm GL}_r(F),\quad
r\geq 1 \end{array}\right\} \]
\[
\left\{\begin{array}{@{}c@{}} W_F\text{-conjugacy classes
of}\\ \text{irreducible smooth representations}\\
\tau:I_F\rightarrow {\rm GL}_m(C),\quad m\geq 1
\end{array}\right\}\longleftrightarrow
\left\{\begin{array}{@{}c@{}} \text{equivalence classes
of}\\ \text{cuspidal representations}\\ {\rm GL}_r(F),\quad
r\geq 1 \end{array}\right\} \]
where two cuspidal representations are said to be equivalent if they differ by the twist by an unramified character. Hence, we obtain a bijection between the Bernstein components of ![]() ${\rm Rep}({\rm GL}_n(F))$ and the connected components of
${\rm Rep}({\rm GL}_n(F))$ and the connected components of ![]() $X_{{\rm GL}_n}^{\rm WD}$. By results of Bushnell and Kutzko [Reference Bushnell and KutzkoBK99] every Bernstein component of
$X_{{\rm GL}_n}^{\rm WD}$. By results of Bushnell and Kutzko [Reference Bushnell and KutzkoBK99] every Bernstein component of ![]() ${\rm Rep}({\rm GL}_n(F))$ can be described by a semi-simple type and the corresponding Hecke algebra is in fact isomorphic to a tensor product of Iwahori–Hecke algebras. This corresponds to the decomposition of the connected components
${\rm Rep}({\rm GL}_n(F))$ can be described by a semi-simple type and the corresponding Hecke algebra is in fact isomorphic to a tensor product of Iwahori–Hecke algebras. This corresponds to the decomposition of the connected components ![]() $X_{\underline {n}}$ of
$X_{\underline {n}}$ of ![]() $X_{{\rm GL}_n}^{\rm WD}$ into a product of spaces of
$X_{{\rm GL}_n}^{\rm WD}$ into a product of spaces of ![]() $(\varphi,N)$-modules. In fact, in the case of
$(\varphi,N)$-modules. In fact, in the case of ![]() ${\rm GL}_n$ type theory and a closer inspection of these decompositions should reduce Conjecture 3.6 to Conjecture 3.2 (in the case of
${\rm GL}_n$ type theory and a closer inspection of these decompositions should reduce Conjecture 3.6 to Conjecture 3.2 (in the case of ![]() ${\rm GL}_r$ for various
${\rm GL}_r$ for various ![]() $r$). In particular, it should be possible to generalize all results proven in the following section for the block
$r$). In particular, it should be possible to generalize all results proven in the following section for the block ![]() ${\rm Rep}_{[T,1]}({\rm GL}_n(F))$ to the whole category
${\rm Rep}_{[T,1]}({\rm GL}_n(F))$ to the whole category ![]() ${\rm Rep}({\rm GL}_n(F))$. This generalization using type theory is discussed in details in [Reference Ben-Zvi, Chen, Helm and NadlerBCHN20, 5].
${\rm Rep}({\rm GL}_n(F))$. This generalization using type theory is discussed in details in [Reference Ben-Zvi, Chen, Helm and NadlerBCHN20, 5].
4. The case of  ${\rm GL}_n$
${\rm GL}_n$
In this section we consider the group ![]() $G={\rm GL}_n(F)$ and make Conjecture 3.2 more explicit in this case. We will provide a candidate for the conjectured functor and prove that it satisfies compatibility with parabolic induction on the dense open subset of regular elements. In the case of
$G={\rm GL}_n(F)$ and make Conjecture 3.2 more explicit in this case. We will provide a candidate for the conjectured functor and prove that it satisfies compatibility with parabolic induction on the dense open subset of regular elements. In the case of ![]() $\operatorname {GL}_2$ we give a full proof of the conjecture.
$\operatorname {GL}_2$ we give a full proof of the conjecture.
We fix ![]() $\mathbb {G}=\operatorname {GL}_n$ and choose the canonical integral model of
$\mathbb {G}=\operatorname {GL}_n$ and choose the canonical integral model of ![]() $\mathbb {G}$ over
$\mathbb {G}$ over ![]() $\mathcal {O}_F$ corresponding to the maximal compact subgroup
$\mathcal {O}_F$ corresponding to the maximal compact subgroup ![]() $K=\operatorname {GL}_n(\mathcal {O}_F)$ of
$K=\operatorname {GL}_n(\mathcal {O}_F)$ of ![]() $G$. In particular, we assume that the hyperspecial vertex defined by
$G$. In particular, we assume that the hyperspecial vertex defined by ![]() $K$ is contained in the apartment defined by the maximal split torus
$K$ is contained in the apartment defined by the maximal split torus ![]() $\mathbb {T}\subset \operatorname {GL}_n$, and
$\mathbb {T}\subset \operatorname {GL}_n$, and ![]() $I\subset K$. We use this to obtain canonical integral models for the choice of a Borel
$I\subset K$. We use this to obtain canonical integral models for the choice of a Borel ![]() $\mathbb {B}\supset \mathbb {T}$ and for parabolic subgroups
$\mathbb {B}\supset \mathbb {T}$ and for parabolic subgroups ![]() $\mathbb {P}\supset \mathbb {B}$ as well as for their Levi quotients. We will use the same symbols for these integral models. We will often simply write
$\mathbb {P}\supset \mathbb {B}$ as well as for their Levi quotients. We will use the same symbols for these integral models. We will often simply write ![]() $\mathfrak {Z}=\mathfrak {Z}_G$ for the Bernstein center of the category
$\mathfrak {Z}=\mathfrak {Z}_G$ for the Bernstein center of the category ![]() ${\rm Rep}_{[T,1]}(G)$.
${\rm Rep}_{[T,1]}(G)$.
4.1 The modified Langlands correspondence
We recall the construction of the modified local Langlands correspondence defined by Breuil and Schneider in [Reference Breuil and SchneiderBS07, 4] (see also [Reference Emerton and HelmEH14, 4.2]). We restrict ourselves to the Bernstein block ![]() ${\rm Rep}_{[T,1]}(G)$.
${\rm Rep}_{[T,1]}(G)$.
Let ![]() $\varpi$ be a uniformizer of
$\varpi$ be a uniformizer of ![]() $F$. For any field extension
$F$. For any field extension ![]() $L$ of
$L$ of ![]() $C$ and
$C$ and ![]() $\lambda \in L^\times$ we write
$\lambda \in L^\times$ we write ![]() ${\rm unr}_\lambda :F^\times \rightarrow L^\times$ for the unramified character mapping
${\rm unr}_\lambda :F^\times \rightarrow L^\times$ for the unramified character mapping ![]() $\varpi$ to
$\varpi$ to ![]() $\lambda$. More generally, for
$\lambda$. More generally, for ![]() $\underline {\lambda }=(\lambda _1,\ldots,\lambda _n)\in (L^\times )^n$ we write
$\underline {\lambda }=(\lambda _1,\ldots,\lambda _n)\in (L^\times )^n$ we write ![]() ${\rm unr}_{\underline {\lambda }}={\rm unr}_{\lambda _1}\otimes \cdots \otimes {\rm unr}_{\lambda _n}:T\rightarrow L^\times$ for the unramified character of the torus
${\rm unr}_{\underline {\lambda }}={\rm unr}_{\lambda _1}\otimes \cdots \otimes {\rm unr}_{\lambda _n}:T\rightarrow L^\times$ for the unramified character of the torus ![]() $T=(F^\times )^n$ whose restriction to the
$T=(F^\times )^n$ whose restriction to the ![]() $i$th coordinate is
$i$th coordinate is ![]() ${\rm unr}_{\lambda _i}$.
${\rm unr}_{\lambda _i}$.
Write ![]() $|-|={\rm unr}_{q^{-1}}:F^\times \rightarrow C^\times$ for the unramified character such that
$|-|={\rm unr}_{q^{-1}}:F^\times \rightarrow C^\times$ for the unramified character such that ![]() $|\varpi |=q^{-1}$. Let
$|\varpi |=q^{-1}$. Let ![]() $L$ be a field extension of
$L$ be a field extension of ![]() $C$ and let
$C$ and let ![]() $(\varphi,N)\in X_{\check G}(L)$ be a
$(\varphi,N)\in X_{\check G}(L)$ be a ![]() $(\varphi,N)$-module such that
$(\varphi,N)$-module such that ![]() $\varphi$ is semi-simple. Then Breuil and Schneider associate to
$\varphi$ is semi-simple. Then Breuil and Schneider associate to ![]() $(\varphi,N)$ a smooth, absolutely indecomposable representation
$(\varphi,N)$ a smooth, absolutely indecomposable representation ![]() ${\rm LL^{mod}}(\varphi,N)$ of
${\rm LL^{mod}}(\varphi,N)$ of ![]() ${\rm GL}_n(F)$ with coefficients in
${\rm GL}_n(F)$ with coefficients in ![]() $L$ as follows.
$L$ as follows.
Fix an algebraic closure ![]() $\bar L$ of
$\bar L$ of ![]() $L$. Given a scalar
$L$. Given a scalar ![]() $\lambda \in \bar L^\times$ and
$\lambda \in \bar L^\times$ and ![]() $r\geq 0$, let
$r\geq 0$, let ![]() ${\rm Sp}(\lambda,r)$ denote as usual the
${\rm Sp}(\lambda,r)$ denote as usual the ![]() $(\varphi,N)$-module structure on
$(\varphi,N)$-module structure on ![]() $\bar L^r=\bar Le_0\oplus \cdots \oplus \bar Le_{r-1}$ defined by
$\bar L^r=\bar Le_0\oplus \cdots \oplus \bar Le_{r-1}$ defined by
 \begin{equation} \begin{aligned} \varphi(e_i) & =q^{-i}\lambda,\\ N(e_i) & =\begin{cases} e_{i+1}, & i< r-1,\\ 0, & i=r-1.\end{cases} \end{aligned} \end{equation}
\begin{equation} \begin{aligned} \varphi(e_i) & =q^{-i}\lambda,\\ N(e_i) & =\begin{cases} e_{i+1}, & i< r-1,\\ 0, & i=r-1.\end{cases} \end{aligned} \end{equation}
Let ![]() ${\rm St}(\lambda,r)$ denote the generalized Steinberg representation of
${\rm St}(\lambda,r)$ denote the generalized Steinberg representation of ![]() ${\rm GL}_r(F)$ with coefficients in
${\rm GL}_r(F)$ with coefficients in ![]() $\bar L$, that is, the unique simple quotient of
$\bar L$, that is, the unique simple quotient of ![]() $\iota _B^G({\rm unr}_\lambda \otimes {\rm unr}_\lambda |-|\otimes \cdots \otimes {\rm unr}_\lambda |-|^{n-1})$.
$\iota _B^G({\rm unr}_\lambda \otimes {\rm unr}_\lambda |-|\otimes \cdots \otimes {\rm unr}_\lambda |-|^{n-1})$.
Given some ![]() $(\varphi,N)\in X_{\check G}(L)$ with
$(\varphi,N)\in X_{\check G}(L)$ with ![]() $\varphi$ semi-simple, we decompose (after enlarging
$\varphi$ semi-simple, we decompose (after enlarging ![]() $L$ if necessary)
$L$ if necessary)
 \[ (L^n,\varphi,N)\cong\bigoplus_{i=1}^s {\rm Sp}(\lambda_i,r_i) \]
\[ (L^n,\varphi,N)\cong\bigoplus_{i=1}^s {\rm Sp}(\lambda_i,r_i) \]
and define ![]() ${\rm LL}^{\rm mod}(\varphi,N)$ as the unique
${\rm LL}^{\rm mod}(\varphi,N)$ as the unique ![]() $L$-model of the
$L$-model of the ![]() $\bar L$ representation
$\bar L$ representation
Here ![]() $P$ is the block upper triangular parabolic whose Levi quotient is identified with the block diagonal subgroup
$P$ is the block upper triangular parabolic whose Levi quotient is identified with the block diagonal subgroup ![]() ${\rm GL}_{r_1}\times \cdots \times {\rm GL}_{r_s}$ and the
${\rm GL}_{r_1}\times \cdots \times {\rm GL}_{r_s}$ and the ![]() $\lambda _i$ are ordered so that they satisfy the condition of [Reference KudlaKud94, Definition 1.2.4].
$\lambda _i$ are ordered so that they satisfy the condition of [Reference KudlaKud94, Definition 1.2.4].
Remark 4.1 Note that the normalization we use differs from the one in [Reference Breuil and SchneiderBS07, Reference Emerton and HelmEH14]. There the representation ![]() ${\rm LL^{mod}}(\varphi,N)$ is modified by the twist by
${\rm LL^{mod}}(\varphi,N)$ is modified by the twist by ![]() $|\det |^{-(n-1)/2}$. This has the advantage that the resulting
$|\det |^{-(n-1)/2}$. This has the advantage that the resulting ![]() $\operatorname {GL}_n(F)$ representation has a unique model over
$\operatorname {GL}_n(F)$ representation has a unique model over ![]() $L$, without assuming the existence (or fixing a choice) of
$L$, without assuming the existence (or fixing a choice) of ![]() $q^{1/2}$, as proven in [Reference Breuil and SchneiderBS07, Lemma 4.2]. As we have fixed a choice
$q^{1/2}$, as proven in [Reference Breuil and SchneiderBS07, Lemma 4.2]. As we have fixed a choice ![]() $q^{1/2}$ in the base field
$q^{1/2}$ in the base field ![]() $C$, and hence a choice of
$C$, and hence a choice of ![]() $|\det |^{-(n-1)/2}$, their argument also implies that our representation
$|\det |^{-(n-1)/2}$, their argument also implies that our representation ![]() ${\rm LL^{mod}}(\varphi,N)$ has a (unique) model over
${\rm LL^{mod}}(\varphi,N)$ has a (unique) model over ![]() $L$. The reason for these two different normalizations is the following. In [Reference Breuil and SchneiderBS07] the representation should be canonically defined over
$L$. The reason for these two different normalizations is the following. In [Reference Breuil and SchneiderBS07] the representation should be canonically defined over ![]() $L$, without choosing
$L$, without choosing ![]() $q^{1/2}$; moreover, in [Reference Emerton and HelmEH14] the representations should (conjecturally) satisfy some local-global compatibility. In our case we work purely locally and we are aiming for a compatibility with normalized parabolic induction. More precisely, we need Lemma 4.3 below to be true as stated (i.e. not a twisted version of it). Anyway, the definition of normalized parabolic induction forces us to choose a square root
$q^{1/2}$; moreover, in [Reference Emerton and HelmEH14] the representations should (conjecturally) satisfy some local-global compatibility. In our case we work purely locally and we are aiming for a compatibility with normalized parabolic induction. More precisely, we need Lemma 4.3 below to be true as stated (i.e. not a twisted version of it). Anyway, the definition of normalized parabolic induction forces us to choose a square root ![]() $q^{1/2}$.
$q^{1/2}$.
If ![]() $(\varphi,N)\in X_{\check G}$ with non-semi-simple
$(\varphi,N)\in X_{\check G}$ with non-semi-simple ![]() $\varphi$, we write
$\varphi$, we write ![]() ${\rm LL^{\rm mod}}(\varphi,N)={\rm LL^{mod}}(\varphi ^{\rm ss},N)$. Moreover, if
${\rm LL^{\rm mod}}(\varphi,N)={\rm LL^{mod}}(\varphi ^{\rm ss},N)$. Moreover, if ![]() $(\varphi,N)$ is such that
$(\varphi,N)$ is such that ![]() ${\rm LL}^{\rm mod}(\varphi,N)$ is absolutely irreducible (i.e. if the
${\rm LL}^{\rm mod}(\varphi,N)$ is absolutely irreducible (i.e. if the ![]() $\check G$-conjugacy class
$\check G$-conjugacy class ![]() $[\varphi ^{\rm ss},N]$ is a generic L-parameter), we usually just write
$[\varphi ^{\rm ss},N]$ is a generic L-parameter), we usually just write ![]() ${\rm LL}(\varphi,N)$ instead of
${\rm LL}(\varphi,N)$ instead of ![]() ${\rm LL^{mod}}(\varphi,N)$. Note that in this case
${\rm LL^{mod}}(\varphi,N)$. Note that in this case ![]() ${\rm LL}(\varphi,N)^\vee \cong {\rm LL}((\varphi,N)^\vee )$, as normalized parabolic induction commutes with contragredients and as in this case the parabolic induction of the contragredient representation still satisfies the condition of [Reference KudlaKud94, Definition 1.2.4].
${\rm LL}(\varphi,N)^\vee \cong {\rm LL}((\varphi,N)^\vee )$, as normalized parabolic induction commutes with contragredients and as in this case the parabolic induction of the contragredient representation still satisfies the condition of [Reference KudlaKud94, Definition 1.2.4].
Lemma 4.2 Let ![]() $x=(\varphi _x,N_x)\in X_{\check G}$. Then, using the notation of (3.1), the center
$x=(\varphi _x,N_x)\in X_{\check G}$. Then, using the notation of (3.1), the center ![]() $\mathfrak {Z}$ acts on the representation
$\mathfrak {Z}$ acts on the representation ![]() ${\rm LL^{mod}}((\varphi,N)^\vee )^\vee$ via the character
${\rm LL^{mod}}((\varphi,N)^\vee )^\vee$ via the character ![]() $\chi _x:\mathfrak {Z}\rightarrow k(x)$ of
$\chi _x:\mathfrak {Z}\rightarrow k(x)$ of ![]() $\mathfrak {Z}$ that is defined by the point
$\mathfrak {Z}$ that is defined by the point ![]() $\chi (x)\in \check T/W=\operatorname {Spec} \mathfrak {Z}$
$\chi (x)\in \check T/W=\operatorname {Spec} \mathfrak {Z}$
Proof. By definition of ![]() ${\rm LL^{mod}}$ we may assume that
${\rm LL^{mod}}$ we may assume that ![]() $\varphi$ is semi-simple. Then the representation
$\varphi$ is semi-simple. Then the representation ![]() ${\rm LL^{mod}}((\varphi,N)^\vee )^\vee$ embeds into
${\rm LL^{mod}}((\varphi,N)^\vee )^\vee$ embeds into
for some ordering ![]() $\underline {\lambda }=(\lambda _1,\ldots,\lambda _n)$ of the eigenvalues of
$\underline {\lambda }=(\lambda _1,\ldots,\lambda _n)$ of the eigenvalues of ![]() $\varphi$. Hence, it follows that
$\varphi$. Hence, it follows that ![]() $({\rm LL^{mod}}((\varphi,N)^\vee )^\vee )^I$ embeds into
$({\rm LL^{mod}}((\varphi,N)^\vee )^\vee )^I$ embeds into ![]() $\mathcal {H}_G\otimes _{\mathcal {H}_T}{\rm unr}_{\underline {\lambda }}$ and it is enough to prove that
$\mathcal {H}_G\otimes _{\mathcal {H}_T}{\rm unr}_{\underline {\lambda }}$ and it is enough to prove that ![]() $\mathfrak {Z}\subset \mathcal {H}_G$ acts on
$\mathfrak {Z}\subset \mathcal {H}_G$ acts on ![]() $\mathcal {H}_G\otimes _{\mathcal {H}_T}{\rm unr}_{\underline {\lambda }}$ as asserted. But as
$\mathcal {H}_G\otimes _{\mathcal {H}_T}{\rm unr}_{\underline {\lambda }}$ as asserted. But as ![]() $\mathfrak {Z}\subset \mathcal {H}_T$ is the center of
$\mathfrak {Z}\subset \mathcal {H}_T$ is the center of ![]() $\mathcal {H}_G$, it acts on
$\mathcal {H}_G$, it acts on ![]() $\mathcal {H}_G\otimes _{\mathcal {H}_T}{\rm unr}_{\lambda }$ via the same character as on
$\mathcal {H}_G\otimes _{\mathcal {H}_T}{\rm unr}_{\lambda }$ via the same character as on ![]() ${\rm unr}_{\underline {\lambda }}$. The claim follows from this.
${\rm unr}_{\underline {\lambda }}$. The claim follows from this.
Recall that for a regular semi-simple endomorphism ![]() $\varphi$ of an
$\varphi$ of an ![]() $L$-vector space
$L$-vector space ![]() $L^n$ with eigenvalues in
$L^n$ with eigenvalues in ![]() $L$ there is a canonical bijection
$L$ there is a canonical bijection
If ![]() $\mathcal {F}$ is a flag corresponding to an ordering
$\mathcal {F}$ is a flag corresponding to an ordering ![]() $\underline {\lambda }=(\lambda _1,\ldots,\lambda _n)$ of the eigenvalues of
$\underline {\lambda }=(\lambda _1,\ldots,\lambda _n)$ of the eigenvalues of ![]() $\varphi$, we denote by
$\varphi$, we denote by ![]() ${\rm unr}_{\mathcal {F}}={\rm unr}_{\underline {\lambda }}$ the
${\rm unr}_{\mathcal {F}}={\rm unr}_{\underline {\lambda }}$ the ![]() $L$-valued unramified character defined by this ordering.
$L$-valued unramified character defined by this ordering.
Lemma 4.3 Let ![]() $x=(\varphi _x,N_x)\in X_{\check G}$ with
$x=(\varphi _x,N_x)\in X_{\check G}$ with ![]() $\varphi _x$ regular semi-simple and let
$\varphi _x$ regular semi-simple and let ![]() $L$ be an (algebraic) extension of
$L$ be an (algebraic) extension of ![]() $k(x)$ containing the eigenvalues of
$k(x)$ containing the eigenvalues of ![]() $\varphi _x$. Then
$\varphi _x$. Then
where the direct sum runs over all flags of ![]() $L^n$ stable under
$L^n$ stable under ![]() $\varphi _x$ and
$\varphi _x$ and ![]() $N_x$.
$N_x$.
Proof. The lemma is an application of the geometrical lemma [Reference Bernstein and ZelevinskyBZ77, 2.11, p. 448] describing the composition of parabolic induction with the Jacquet functor.
Assume first that ![]() $(\varphi,N)\otimes _{k(x)}L={\rm Sp}(\lambda,r)$ (see (4.1)). Then we need to compute the Jacquet module of the generalized Steinberg representation
$(\varphi,N)\otimes _{k(x)}L={\rm Sp}(\lambda,r)$ (see (4.1)). Then we need to compute the Jacquet module of the generalized Steinberg representation
Here we view ![]() ${\rm unr}_\lambda |-|^{(n-1)/2}$ as a character of
${\rm unr}_\lambda |-|^{(n-1)/2}$ as a character of ![]() $M$ for any (standard) Levi
$M$ for any (standard) Levi ![]() $M$. Computing
$M$. Computing ![]() $r_B^G(\iota _P^G(\delta ^{-1/2}\otimes {\rm unr}_\lambda |-|^{(n-1)/2}))$ using the geometrical lemma of [Reference Bernstein and ZelevinskyBZ77], it follows that
$r_B^G(\iota _P^G(\delta ^{-1/2}\otimes {\rm unr}_\lambda |-|^{(n-1)/2}))$ using the geometrical lemma of [Reference Bernstein and ZelevinskyBZ77], it follows that
This is the character corresponding to the ordering ![]() $q^{-(r-1)} \lambda,\ldots,\lambda q^{-1},\lambda$, that is, to the ordering defined by the unique
$q^{-(r-1)} \lambda,\ldots,\lambda q^{-1},\lambda$, that is, to the ordering defined by the unique ![]() $(\varphi,N)$-stable flag of
$(\varphi,N)$-stable flag of ![]() ${\rm Sp}(\lambda,r)$.
${\rm Sp}(\lambda,r)$.
In the general case we decompose ![]() $(\varphi,N)\otimes _{k(x)}L=\bigoplus _{i=1}^s {\rm St}(\lambda _i,r_i)$ and write
$(\varphi,N)\otimes _{k(x)}L=\bigoplus _{i=1}^s {\rm St}(\lambda _i,r_i)$ and write
as in (4.2). Then again the geometrical lemma of [Reference Bernstein and ZelevinskyBZ77] computes that its Jacquet module is the desired one, and the claim follows from compatibility with contragredients.
Remark 4.4 For ![]() $C=\mathbb {C}$ the lemma can be interpreted as a consequence of the classification of Kazhdan and Lusztig [Reference Kazhdan and LusztigKL87] using equivariant
$C=\mathbb {C}$ the lemma can be interpreted as a consequence of the classification of Kazhdan and Lusztig [Reference Kazhdan and LusztigKL87] using equivariant ![]() $K$-theory, or its formulation using Borel–Moore homology in [Reference Chriss and GinzburgCG97, 8.1]. For
$K$-theory, or its formulation using Borel–Moore homology in [Reference Chriss and GinzburgCG97, 8.1]. For ![]() $(\varphi,N)\in X_{\check G}(C)$ as in the lemma the fiber
$(\varphi,N)\in X_{\check G}(C)$ as in the lemma the fiber ![]() $\tilde \beta _{\check B}^{-1}(\varphi,N)$ of the map
$\tilde \beta _{\check B}^{-1}(\varphi,N)$ of the map ![]() $\tilde \beta _{\check B}:\tilde X_{\check B}\rightarrow X_{\check G}$ is identified with the
$\tilde \beta _{\check B}:\tilde X_{\check B}\rightarrow X_{\check G}$ is identified with the ![]() $\varphi$-fixed points
$\varphi$-fixed points ![]() $\mathfrak {B}_N^\varphi$ of the variety
$\mathfrak {B}_N^\varphi$ of the variety ![]() $\mathfrak {B}_N$ of
$\mathfrak {B}_N$ of ![]() $N$-stable complete flags, compare [Reference Chriss and GinzburgCG97, 8.1]. Using the induction theorem [Reference Kazhdan and LusztigKL87, 6] one can deduce that the
$N$-stable complete flags, compare [Reference Chriss and GinzburgCG97, 8.1]. Using the induction theorem [Reference Kazhdan and LusztigKL87, 6] one can deduce that the ![]() $\mathcal {H}_G$-module
$\mathcal {H}_G$-module ![]() ${\rm LL^{mod}}(\varphi,N)$ is precisely the standard module constructed in [Reference Chriss and GinzburgCG97, Definition 8.1.9](note that the group
${\rm LL^{mod}}(\varphi,N)$ is precisely the standard module constructed in [Reference Chriss and GinzburgCG97, Definition 8.1.9](note that the group ![]() $C(\varphi,N)$ in that definition is trivial in the
$C(\varphi,N)$ in that definition is trivial in the ![]() ${\rm GL}_n$ case). However, as
${\rm GL}_n$ case). However, as ![]() $\varphi$ is regular semi-simple the variety
$\varphi$ is regular semi-simple the variety ![]() $\mathfrak {B}_N^\varphi$ is a finite union of points, namely, the complete
$\mathfrak {B}_N^\varphi$ is a finite union of points, namely, the complete ![]() $(\varphi,N)$-stable flags. Hence, its Borel-Moore homology is the direct sum of copies of
$(\varphi,N)$-stable flags. Hence, its Borel-Moore homology is the direct sum of copies of ![]() $C$ indexed by these points. By construction the Hecke algebra
$C$ indexed by these points. By construction the Hecke algebra ![]() $\mathcal {H}_T$ acts on this direct sum as asserted in the lemma.
$\mathcal {H}_T$ acts on this direct sum as asserted in the lemma.
4.2 The work of Helm and of Emerton and Helm
Emerton and Helm [Reference Emerton and HelmEH14] proposed the existence of a family of ![]() $G$-representations over a deformation space of
$G$-representations over a deformation space of ![]() $\ell$-adic Galois (or Weil–Deligne) representations that interpolates the modified local Langlands correspondence in a certain sense. A candidate for such a family was constructed in subsequent work of Helm [Reference HelmHel16].Footnote 7 Rather than working over
$\ell$-adic Galois (or Weil–Deligne) representations that interpolates the modified local Langlands correspondence in a certain sense. A candidate for such a family was constructed in subsequent work of Helm [Reference HelmHel16].Footnote 7 Rather than working over ![]() $\ell$-adic deformation rings we want to work with the stacks of L-parameters defined above. We review the work of Emerton and Helm and of Helm in this setup in order to construct a family of
$\ell$-adic deformation rings we want to work with the stacks of L-parameters defined above. We review the work of Emerton and Helm and of Helm in this setup in order to construct a family of ![]() $G$-representation on the stack
$G$-representation on the stack ![]() $[X_{\check G}/\check G]$.
$[X_{\check G}/\check G]$.
In this subsection we need to work with families of admissible smooth representations (compare [Reference Emerton and HelmEH14, 2.1]). We make precise what we mean by this. Let ![]() $A$ be a noetherian
$A$ be a noetherian ![]() $C$-algebra and let
$C$-algebra and let ![]() $V$ be a finitely generated
$V$ be a finitely generated ![]() $A[G]$-module. We say that
$A[G]$-module. We say that ![]() $V$ is an admissible smooth family of
$V$ is an admissible smooth family of ![]() $G$ representations over
$G$ representations over ![]() $A$ if the
$A$ if the ![]() $G$-representation on
$G$-representation on ![]() $V$ is smooth and if
$V$ is smooth and if ![]() $V^{K'}$ is a finitely generated
$V^{K'}$ is a finitely generated ![]() $A$-module for every compact open subgroup
$A$-module for every compact open subgroup ![]() $K'\subset G$.
$K'\subset G$.
Denote by ![]() $N\subset B$ the unipotent radical and let
$N\subset B$ the unipotent radical and let ![]() $\psi :N\rightarrow C^\times$ be a generic character. Recall that an irreducible
$\psi :N\rightarrow C^\times$ be a generic character. Recall that an irreducible ![]() $G$-representation
$G$-representation ![]() $\pi$ is called generic if there exists an embedding
$\pi$ is called generic if there exists an embedding ![]() $\pi \hookrightarrow {\rm Ind}_N^G\psi$. Equivalently,
$\pi \hookrightarrow {\rm Ind}_N^G\psi$. Equivalently, ![]() $\pi$ is generic if there is a surjection
$\pi$ is generic if there is a surjection ![]() $\operatorname {c-ind}_N^G\psi \twoheadrightarrow \pi$.
$\operatorname {c-ind}_N^G\psi \twoheadrightarrow \pi$.
We write ![]() $(\operatorname {c-ind}_N^G\psi )_{[T,1]}$ for the image of the compactly induced representation
$(\operatorname {c-ind}_N^G\psi )_{[T,1]}$ for the image of the compactly induced representation ![]() $\operatorname {c-ind}_N^G\psi$ in the Bernstein component
$\operatorname {c-ind}_N^G\psi$ in the Bernstein component ![]() ${\rm Rep}_{[T,1]}(G)={\rm Rep}^IG$. As in the case of
${\rm Rep}_{[T,1]}(G)={\rm Rep}^IG$. As in the case of ![]() ${\rm GL}_n$ a Whittaker datum is unique up to isomorphism, this representation (up to isomorphism) does not depend on the Whittaker datum
${\rm GL}_n$ a Whittaker datum is unique up to isomorphism, this representation (up to isomorphism) does not depend on the Whittaker datum ![]() $(B,\psi )$.
$(B,\psi )$.
Recall that we have fixed ![]() $K=\operatorname {GL}_n(\mathcal {O}_F)\supset I$ and consider the induced representation
$K=\operatorname {GL}_n(\mathcal {O}_F)\supset I$ and consider the induced representation ![]() ${\rm Ind}_I^K \mathbf {1}_I$. By [Reference Schneider and ZinkSZ99] this induced representation decomposes into a direct sum
${\rm Ind}_I^K \mathbf {1}_I$. By [Reference Schneider and ZinkSZ99] this induced representation decomposes into a direct sum
indexed by the set of partitions ![]() $\mathcal {P}$ of the positive integer
$\mathcal {P}$ of the positive integer ![]() $n$ which is partially ordered (see [Reference Schneider and ZinkSZ99, p. 169]) and has a unique minimalFootnote 8 element
$n$ which is partially ordered (see [Reference Schneider and ZinkSZ99, p. 169]) and has a unique minimalFootnote 8 element ![]() $\mathcal {P}_{\rm min}$ and a unique maximal element
$\mathcal {P}_{\rm min}$ and a unique maximal element ![]() $\mathcal {P}_{\rm max}$. Let
$\mathcal {P}_{\rm max}$. Let ![]() ${\rm st}={\rm st}_G=\sigma _{\mathcal {P}_{\rm min}}$ denote the finite-dimensional Steinberg representation. This representation occurs with multiplicity
${\rm st}={\rm st}_G=\sigma _{\mathcal {P}_{\rm min}}$ denote the finite-dimensional Steinberg representation. This representation occurs with multiplicity ![]() $m_{\mathcal {P}_{\rm min}}=1$. As
$m_{\mathcal {P}_{\rm min}}=1$. As ![]() $\operatorname {c-ind}_K^G{\rm st}$ lies in the Bernstein component
$\operatorname {c-ind}_K^G{\rm st}$ lies in the Bernstein component ![]() $[T,1]$ it carries a natural action of
$[T,1]$ it carries a natural action of ![]() $\mathfrak {Z}$.
$\mathfrak {Z}$.
We further recall from [Reference Bernstein and ZelevinskyBZ77, 3.2 and 3.5] the definition of the ![]() $r$th derivative
$r$th derivative ![]() $V^{(r)}$ of a
$V^{(r)}$ of a ![]() ${\rm GL}_n(F)$-representation
${\rm GL}_n(F)$-representation ![]() $V$ which is a smooth representation of
$V$ which is a smooth representation of ![]() ${\rm GL}_{n-r}(F)$. In particular,
${\rm GL}_{n-r}(F)$. In particular, ![]() $V^{(n)}$ is just a
$V^{(n)}$ is just a ![]() $C$-vector space. By [Reference HelmHel16, p.5, (2)] there is natural isomorphism
$C$-vector space. By [Reference HelmHel16, p.5, (2)] there is natural isomorphism
If ![]() $0\neq v\in V^{(n)}$ and
$0\neq v\in V^{(n)}$ and ![]() $V$ lies in the Bernstein component
$V$ lies in the Bernstein component ![]() $[T,1]$, then the morphism defined by
$[T,1]$, then the morphism defined by ![]() $v$ obviously factors through
$v$ obviously factors through ![]() $(\operatorname {c-ind}_I^G\psi )_{[T,1]}$.
$(\operatorname {c-ind}_I^G\psi )_{[T,1]}$.
The following theorem is a summary of the results in [Reference HelmHel16, §§ 3,4] (translated to the easier situation considered here).
Theorem 4.5 Let ![]() $\pi$ be one of the representations
$\pi$ be one of the representations ![]() $(\operatorname {c-ind}_N^G\psi )_{[T,1]}$ and
$(\operatorname {c-ind}_N^G\psi )_{[T,1]}$ and ![]() $\operatorname {c-ind}_K^G{\rm st}$. Then
$\operatorname {c-ind}_K^G{\rm st}$. Then ![]() $\pi$ is a smooth
$\pi$ is a smooth ![]() $\mathfrak {Z}$-representation and the
$\mathfrak {Z}$-representation and the ![]() $n$th derivative
$n$th derivative ![]() $\pi ^{(n)}$ is a free
$\pi ^{(n)}$ is a free ![]() $\mathfrak {Z}$-module of rank one. Moreover, let
$\mathfrak {Z}$-module of rank one. Moreover, let ![]() $\mathfrak {p}\in {\rm Spec}\,\mathfrak {Z}$. Then the following properties hold.
$\mathfrak {p}\in {\rm Spec}\,\mathfrak {Z}$. Then the following properties hold.
(a) The representation
 $\pi \otimes k(\mathfrak {p})$ is a direct sum of finite-length representations.
$\pi \otimes k(\mathfrak {p})$ is a direct sum of finite-length representations.(b) The cosocle
 ${\rm cosoc}(\mathfrak {p})$ of
${\rm cosoc}(\mathfrak {p})$ of  $\pi \otimes k(\mathfrak {p})$ is absolutely irreducible and generic.
$\pi \otimes k(\mathfrak {p})$ is absolutely irreducible and generic.(c) The representation
 $\ker (\pi \otimes k(\mathfrak {p})\rightarrow {\rm cosoc}(\mathfrak {p}))$ does not contain any generic subquotient.
$\ker (\pi \otimes k(\mathfrak {p})\rightarrow {\rm cosoc}(\mathfrak {p}))$ does not contain any generic subquotient.
Finally, the representation ![]() $\operatorname {c-ind}_K^G{\rm st}$ is admissible as a
$\operatorname {c-ind}_K^G{\rm st}$ is admissible as a ![]() $\mathfrak {Z}$-representation.
$\mathfrak {Z}$-representation.
Proof. We cite the proof from [Reference HelmHel16]. All references in this proof refer to that paper. In Helm's situation the coefficients are ![]() $W(k)$ for a finite field
$W(k)$ for a finite field ![]() $k$, instead of the characteristic-zero field
$k$, instead of the characteristic-zero field ![]() $C$ in our case. The arguments literally do not change in our setup; except for one argument, where the classification of irreducible, smooth mod
$C$ in our case. The arguments literally do not change in our setup; except for one argument, where the classification of irreducible, smooth mod ![]() $\ell$ representations in terms of parabolic induction has to be replaced by the corresponding classification of irreducible, smooth representations in characteristic zero.
$\ell$ representations in terms of parabolic induction has to be replaced by the corresponding classification of irreducible, smooth representations in characteristic zero.
The case of ![]() $(\operatorname {c-ind}_I^G\psi )_{[T,1]}$ follows from Lemmas 3.2 and 3.4. In the case
$(\operatorname {c-ind}_I^G\psi )_{[T,1]}$ follows from Lemmas 3.2 and 3.4. In the case ![]() $\pi =\operatorname {c-ind}_K^G{\rm st}$ admissibility follows from Theorem 4.1, and part (a) is Lemma 4.2. Properties (b) and (c) are proven in Proposition 4.9. Finally the claim on
$\pi =\operatorname {c-ind}_K^G{\rm st}$ admissibility follows from Theorem 4.1, and part (a) is Lemma 4.2. Properties (b) and (c) are proven in Proposition 4.9. Finally the claim on ![]() $\pi ^{(n)}$ is Corollary 4.10.
$\pi ^{(n)}$ is Corollary 4.10.
The proof of Helm's Proposition 4.9 uses the classification of irreducible smooth mod ![]() $\ell$ representations of
$\ell$ representations of ![]() ${\rm GL}_n(F)$ in terms of parabolic induction, and has to be replaced by the usual Bernstein–Zelevinsky classification of irreducible, smooth representations in characteristic zero [Reference ZelevinskyZel80]. With this change of reference the proof in [Reference HelmHel16] literally does not change.
${\rm GL}_n(F)$ in terms of parabolic induction, and has to be replaced by the usual Bernstein–Zelevinsky classification of irreducible, smooth representations in characteristic zero [Reference ZelevinskyZel80]. With this change of reference the proof in [Reference HelmHel16] literally does not change.
We note the following consequence (which is also a special case of [Reference Chan and SavinCS19, Theorem 1.1]) of the results in Theorem 4.5.
Corollary 4.6 There is an isomorphism of ![]() $\mathfrak {Z}[G]$-modules,
$\mathfrak {Z}[G]$-modules,
unique up to a scalar in ![]() $\mathfrak {Z}^\times$.
$\mathfrak {Z}^\times$.
Proof. By Theorem 4.5 the ![]() $n$th derivative
$n$th derivative ![]() $(\operatorname {c-ind}_K^G{\rm st})^{(n)}$ is locally free of rank one over
$(\operatorname {c-ind}_K^G{\rm st})^{(n)}$ is locally free of rank one over ![]() $\mathfrak {Z}$. As
$\mathfrak {Z}$. As ![]() $\mathfrak {Z}\cong C[X_1,\ldots, X_{n-1},X_n^{\pm 1}]$ every line bundle on
$\mathfrak {Z}\cong C[X_1,\ldots, X_{n-1},X_n^{\pm 1}]$ every line bundle on ![]() $\operatorname {Spec}\mathfrak {Z}$ is trivial and hence
$\operatorname {Spec}\mathfrak {Z}$ is trivial and hence ![]() $(\operatorname {c-ind}_K^G{\rm st})^{(n)}\cong \mathfrak {Z}$. By the discussion preceding Theorem 4.5, a choice of a basis vector (which is unique up to a scalar in
$(\operatorname {c-ind}_K^G{\rm st})^{(n)}\cong \mathfrak {Z}$. By the discussion preceding Theorem 4.5, a choice of a basis vector (which is unique up to a scalar in ![]() $\mathfrak {Z}^\times$) gives rise to a morphism
$\mathfrak {Z}^\times$) gives rise to a morphism
We claim that ![]() $\alpha$ is an isomorphism.
$\alpha$ is an isomorphism.
We first show that ![]() $\alpha$ is surjective. Let
$\alpha$ is surjective. Let ![]() $W$ denote the cokernel of
$W$ denote the cokernel of ![]() $\alpha$. Then
$\alpha$. Then ![]() $W$ is generated by its Iwahori fixed vectors
$W$ is generated by its Iwahori fixed vectors ![]() $W^I$ and, by admissibility of
$W^I$ and, by admissibility of ![]() $\operatorname {c-ind}_K^G{\rm st}$, the
$\operatorname {c-ind}_K^G{\rm st}$, the ![]() $\mathfrak {Z}$-module
$\mathfrak {Z}$-module ![]() $W^I$ is finitely generated.
$W^I$ is finitely generated.
As ![]() $(-)^I$ is an exact functor,
$(-)^I$ is an exact functor, ![]() $W^I\otimes k(\mathfrak {p})=(W\otimes k(\mathfrak {p}))^I$ and hence
$W^I\otimes k(\mathfrak {p})=(W\otimes k(\mathfrak {p}))^I$ and hence ![]() $W=0$ if and only if
$W=0$ if and only if ![]() $W\otimes k(\mathfrak {p})=0$ for all
$W\otimes k(\mathfrak {p})=0$ for all ![]() $\mathfrak {p}\in {\rm Spec}\, \mathfrak {Z}$.
$\mathfrak {p}\in {\rm Spec}\, \mathfrak {Z}$.
As ![]() $\alpha$ by definition induces an isomorphism
$\alpha$ by definition induces an isomorphism
and as the functor ![]() $(-)^{(n)}$ is exact (see, for example, [Reference Bernstein and ZelevinskyBZ77, 3.2, Proposition]), it follows that
$(-)^{(n)}$ is exact (see, for example, [Reference Bernstein and ZelevinskyBZ77, 3.2, Proposition]), it follows that ![]() $W^{(n)}=0$ and
$W^{(n)}=0$ and ![]() $(W\otimes k(\mathfrak {p}))^{(n)}=0$ for all
$(W\otimes k(\mathfrak {p}))^{(n)}=0$ for all ![]() $\mathfrak {p}\in {\rm Spec}\, \mathfrak {Z}$. Assume that
$\mathfrak {p}\in {\rm Spec}\, \mathfrak {Z}$. Assume that ![]() $W\otimes k(\mathfrak {p})\neq 0$. As
$W\otimes k(\mathfrak {p})\neq 0$. As ![]() $W\otimes k(\mathfrak {p})$ is a quotient of
$W\otimes k(\mathfrak {p})$ is a quotient of ![]() $\operatorname {c-ind}_K^G{\rm st}\otimes k(\mathfrak {p})$, Theorem 4.5(b),(c) implies that there exists a non-zero morphism
$\operatorname {c-ind}_K^G{\rm st}\otimes k(\mathfrak {p})$, Theorem 4.5(b),(c) implies that there exists a non-zero morphism
contradicting ![]() $(W\otimes k(\mathfrak {p}))^{(n)}=0$
$(W\otimes k(\mathfrak {p}))^{(n)}=0$
Now ![]() $\operatorname {c-ind}_K^G {\rm st}$ is projective as a
$\operatorname {c-ind}_K^G {\rm st}$ is projective as a ![]() $G$-representation and hence the surjection
$G$-representation and hence the surjection ![]() $\alpha$ has a splitting
$\alpha$ has a splitting
As ![]() $\alpha$ induces an isomorphism after applying the
$\alpha$ induces an isomorphism after applying the ![]() $n$th derivative
$n$th derivative ![]() $(-)^{(n)}$, it follows that
$(-)^{(n)}$, it follows that ![]() $(W')^{(n)}=0$. By the adjointness property (4.5) is follows that the canonical projection
$(W')^{(n)}=0$. By the adjointness property (4.5) is follows that the canonical projection
is zero and hence ![]() $W'=0$, as
$W'=0$, as ![]() $\beta$ is surjective.
$\beta$ is surjective.
Following [Reference HelmHel16], we construct a family ![]() $\mathcal {V}_G$ of
$\mathcal {V}_G$ of ![]() $G$-representations on
$G$-representations on ![]() $[X_{\check G}/\check G]$ that conjecturally interpolates the modified local Langlands correspondence (see Conjecture 4.8 below for the precise meaning). Rather than constructing
$[X_{\check G}/\check G]$ that conjecturally interpolates the modified local Langlands correspondence (see Conjecture 4.8 below for the precise meaning). Rather than constructing ![]() $\mathcal {V}_G$ directly on
$\mathcal {V}_G$ directly on ![]() $[X_{\check G}/\check G]$ we construct a family
$[X_{\check G}/\check G]$ we construct a family ![]() $\tilde {\mathcal {V}}_G$ on the affine scheme
$\tilde {\mathcal {V}}_G$ on the affine scheme ![]() $X_{\check G}=:{\rm Spec}\, A_{\check G}$ that is
$X_{\check G}=:{\rm Spec}\, A_{\check G}$ that is ![]() $\check G$-equivariant and hence descends to
$\check G$-equivariant and hence descends to ![]() $[X_{\check G}/\check G]$.
$[X_{\check G}/\check G]$.
Lemma 4.7 Let ![]() $x=(\varphi _x,N_x)\in X_{\check G}$. There exists a canonical surjection
$x=(\varphi _x,N_x)\in X_{\check G}$. There exists a canonical surjection
that is unique up to a scalar.
Proof. This follows from the argument in the proof of [Reference HelmHel16, Theorem 7.9], using Lemma 4.2 instead of [Reference HelmHel16, Conjecture 7.5].
Let ![]() $\eta =(\varphi _\eta,N_\eta )\in X_{\check G}$ be a generic point. Then
$\eta =(\varphi _\eta,N_\eta )\in X_{\check G}$ be a generic point. Then
is an irreducible generic representation. We obtain a morphism
where the second morphism is the choice of a surjection as in Lemma 4.7.
Let ![]() $\eta _i$,
$\eta _i$, ![]() $i\in I$, denote the generic points of
$i\in I$, denote the generic points of ![]() $X_{\check G}=\operatorname {Spec} A_{\check G}$. We define
$X_{\check G}=\operatorname {Spec} A_{\check G}$. We define ![]() $\tilde {\mathcal {V}}_{G}$ to be the (admissible smooth) family of
$\tilde {\mathcal {V}}_{G}$ to be the (admissible smooth) family of ![]() $G$-representations over
$G$-representations over ![]() $A_{\check G}$ that is the image of the morphism
$A_{\check G}$ that is the image of the morphism
Up to isomorphism, this image does not depend on the choice of the surjection
By abuse of notation we also write ![]() $\tilde {\mathcal {V}}_G$ for the corresponding sheaf on
$\tilde {\mathcal {V}}_G$ for the corresponding sheaf on ![]() $X_{\check G}$.
$X_{\check G}$.
It can easily be seen that ![]() $\tilde {\mathcal {V}}_G$ is a
$\tilde {\mathcal {V}}_G$ is a ![]() $\check G$-equivariant quotient of
$\check G$-equivariant quotient of ![]() $(\operatorname {c-ind}_N^G\psi )_{[T,1]}\otimes _{\mathfrak {Z}}A_{\check G}$ (equipped with the obvious
$(\operatorname {c-ind}_N^G\psi )_{[T,1]}\otimes _{\mathfrak {Z}}A_{\check G}$ (equipped with the obvious ![]() $\check G$-equivariant structure). Hence,
$\check G$-equivariant structure). Hence, ![]() $\tilde {\mathcal {V}}_G$ descends to a quasi-coherent sheaf
$\tilde {\mathcal {V}}_G$ descends to a quasi-coherent sheaf ![]() $\mathcal {V}_G$ on
$\mathcal {V}_G$ on ![]() $[X_{\check G}/\check G]$ that carries an action of
$[X_{\check G}/\check G]$ that carries an action of ![]() $G$. We will often refer to this family of
$G$. We will often refer to this family of ![]() $G$-representation as the Emerton–Helm family. Conjecturally this family interpolates the modified local Langlands correspondence.
$G$-representation as the Emerton–Helm family. Conjecturally this family interpolates the modified local Langlands correspondence.
Conjecture 4.8 (compare [Reference Emerton and HelmEH14])
Let ![]() $x=(\varphi,N)\in X_{\check G}$ be any point. Then
$x=(\varphi,N)\in X_{\check G}$ be any point. Then
4.3 Idempotents in the Iwahori–Hecke algebra
We will describe the family of Hecke modules associated to the Emerton–Helm family ![]() $\mathcal {V}_G$ in the next subsection, and relate this construction to Conjecture 3.2. Before we do so, we need some preparation about idempotent elements in the Iwahori–Hecke algebra.
$\mathcal {V}_G$ in the next subsection, and relate this construction to Conjecture 3.2. Before we do so, we need some preparation about idempotent elements in the Iwahori–Hecke algebra.
Let ![]() $J\subset G$ be a compact open subgroup and
$J\subset G$ be a compact open subgroup and ![]() $(\lambda,W)$ be a smooth representation of
$(\lambda,W)$ be a smooth representation of ![]() $J$ on a finite-dimensional
$J$ on a finite-dimensional ![]() $C$-vector space with contragredient representation
$C$-vector space with contragredient representation ![]() $(\lambda ^\vee, W^\vee )$. Then we have a natural identification of
$(\lambda ^\vee, W^\vee )$. Then we have a natural identification of ![]() $C$-algebras
$C$-algebras
 \begin{equation}
\begin{aligned} {\rm
End}_G(\operatorname{c-ind}_J^G\lambda)\cong\left\{\begin{array}{@{}c@{}}
\text{compactly supported}\ f:G\rightarrow {\rm
End}_C(W^\vee)\\ \text{such that}\
f(j_1gj_2)=\lambda^\vee(j_1)\circ f(g)\circ
\lambda^\vee(j_2)\\ \text{for all}\ g\in G,\ j_1,j_2\in J
\end{array}\right\}, \end{aligned}
\end{equation}
\begin{equation}
\begin{aligned} {\rm
End}_G(\operatorname{c-ind}_J^G\lambda)\cong\left\{\begin{array}{@{}c@{}}
\text{compactly supported}\ f:G\rightarrow {\rm
End}_C(W^\vee)\\ \text{such that}\
f(j_1gj_2)=\lambda^\vee(j_1)\circ f(g)\circ
\lambda^\vee(j_2)\\ \text{for all}\ g\in G,\ j_1,j_2\in J
\end{array}\right\}, \end{aligned}
\end{equation}
where, as usual, the algebra structure on the right-hand side is given by convolution. Given ![]() $f\in \mathcal {H}(G,\lambda )$, one defines
$f\in \mathcal {H}(G,\lambda )$, one defines ![]() $\check f:g\mapsto f(g^{-1})^\vee \in {\rm End}_C(W)$. Then
$\check f:g\mapsto f(g^{-1})^\vee \in {\rm End}_C(W)$. Then ![]() $f\mapsto \check f$ induces an isomorphism of
$f\mapsto \check f$ induces an isomorphism of ![]() $C$-algebras
$C$-algebras
Recall that ![]() $\mathcal {H}_G={\rm End}_G(\operatorname {c-ind}_I^G\mathbf {1}_I)={\rm End}_G(\operatorname {c-ind}_K^G V)$, where
$\mathcal {H}_G={\rm End}_G(\operatorname {c-ind}_I^G\mathbf {1}_I)={\rm End}_G(\operatorname {c-ind}_K^G V)$, where ![]() $V={\rm Ind}_I^K\mathbf {1}_I$. From now on we write
$V={\rm Ind}_I^K\mathbf {1}_I$. From now on we write ![]() $\lambda$ for the
$\lambda$ for the ![]() $K$-representation on
$K$-representation on ![]() $V$. As in (4.4), the representation
$V$. As in (4.4), the representation ![]() $V$ decomposes as a direct sum of the representations isomorphic to
$V$ decomposes as a direct sum of the representations isomorphic to ![]() $\sigma _\mathcal {P}$. Note that
$\sigma _\mathcal {P}$. Note that
where ![]() $B(k)\subset {\rm GL}_n(k)$ is the special fiber of the Borel subgroup and
$B(k)\subset {\rm GL}_n(k)$ is the special fiber of the Borel subgroup and ![]() $K$ acts via the quotient map
$K$ acts via the quotient map ![]() $K\rightarrow \operatorname {GL}_n(k)$. For a partition
$K\rightarrow \operatorname {GL}_n(k)$. For a partition ![]() $\mathcal {P}$ we write
$\mathcal {P}$ we write ![]() $\Sigma _\mathcal {P}\subset V$ for the
$\Sigma _\mathcal {P}\subset V$ for the ![]() $\sigma _\mathcal {P}$-isotypical component of
$\sigma _\mathcal {P}$-isotypical component of ![]() $V$. In particular, we have
$V$. In particular, we have ![]() $\Sigma _\mathcal {P}\cong \sigma _\mathcal {P}^{m_\mathcal {P}}$. The direct summand
$\Sigma _\mathcal {P}\cong \sigma _\mathcal {P}^{m_\mathcal {P}}$. The direct summand ![]() $\operatorname {c-ind}_K^G\Sigma _\mathcal {P}$ of
$\operatorname {c-ind}_K^G\Sigma _\mathcal {P}$ of ![]() $\operatorname {c-ind}_K^GV=\operatorname {c-ind}_I^G\mathbf {1}_I$ defines an idempotent element
$\operatorname {c-ind}_K^GV=\operatorname {c-ind}_I^G\mathbf {1}_I$ defines an idempotent element ![]() $e_\mathcal {P}\in \mathcal {H}_G$. If
$e_\mathcal {P}\in \mathcal {H}_G$. If ![]() $\mathcal {P}=\mathcal {P}_{\rm min}$ we will usually write
$\mathcal {P}=\mathcal {P}_{\rm min}$ we will usually write ![]() $e_{\rm st}$ (or
$e_{\rm st}$ (or ![]() $e_{G,{\rm st}}$ if we need to refer to the group
$e_{G,{\rm st}}$ if we need to refer to the group ![]() $G$) instead of
$G$) instead of ![]() $e_{\mathcal {P}_{\rm min}}$. Further, we usually write
$e_{\mathcal {P}_{\rm min}}$. Further, we usually write ![]() $e_K=e_{\mathcal {P}_{\rm max}}$, which is identified with the characteristic function of
$e_K=e_{\mathcal {P}_{\rm max}}$, which is identified with the characteristic function of ![]() $K$.
$K$.
Using the description of the Hecke algebra (4.7), the idempotent elements ![]() $e_\mathcal {P}$ can be described as follows. Let
$e_\mathcal {P}$ can be described as follows. Let ![]() $f_\mathcal {P}:V^\vee \rightarrow V^\vee$ denote the endomorphism that is the identity on
$f_\mathcal {P}:V^\vee \rightarrow V^\vee$ denote the endomorphism that is the identity on ![]() $\Sigma _\mathcal {P}^\vee$ and zero on
$\Sigma _\mathcal {P}^\vee$ and zero on ![]() $\Sigma _{\mathcal {P}'}^\vee$ for
$\Sigma _{\mathcal {P}'}^\vee$ for ![]() $\mathcal {P}'\neq \mathcal {P}$. Then the idempotent element
$\mathcal {P}'\neq \mathcal {P}$. Then the idempotent element ![]() $e_\mathcal {P}$ is defined by
$e_\mathcal {P}$ is defined by
 \[ e_\mathcal{P}:g\longmapsto\begin{cases} 0, & g\notin K,\\ \lambda^\vee(g)\circ f_\mathcal{P}=f_\mathcal{P}\circ \lambda^\vee(g), & g\in K. \end{cases} \]
\[ e_\mathcal{P}:g\longmapsto\begin{cases} 0, & g\notin K,\\ \lambda^\vee(g)\circ f_\mathcal{P}=f_\mathcal{P}\circ \lambda^\vee(g), & g\in K. \end{cases} \]
Note that the representation ![]() $V={\rm Ind}_K^G\mathbf {1}_I$ and the irreducible representations
$V={\rm Ind}_K^G\mathbf {1}_I$ and the irreducible representations ![]() $\sigma _\mathcal {P}$ are self-dual. In the case of
$\sigma _\mathcal {P}$ are self-dual. In the case of ![]() $V$ this follows from the computation of the smooth dual of an induced representation. In particular, the canonical identification
$V$ this follows from the computation of the smooth dual of an induced representation. In particular, the canonical identification ![]() $\mathbf {1}_I=(\mathbf {1}_I)^\vee$ gives a canonical isomorphism
$\mathbf {1}_I=(\mathbf {1}_I)^\vee$ gives a canonical isomorphism ![]() $\alpha :V\rightarrow V^\vee$. In the case of
$\alpha :V\rightarrow V^\vee$. In the case of ![]() $\sigma _\mathcal {P}$ we proceed by descending induction: the claim is obviously true for
$\sigma _\mathcal {P}$ we proceed by descending induction: the claim is obviously true for ![]() $\mathbf {1}_K=\sigma _{\mathcal {P}_{\rm max}}$, and for each
$\mathbf {1}_K=\sigma _{\mathcal {P}_{\rm max}}$, and for each ![]() $\mathcal {P}$ we can find some (integral model of a) parabolic subgroup
$\mathcal {P}$ we can find some (integral model of a) parabolic subgroup ![]() $\mathbb {P}\subset {\rm GL}_n$ such that
$\mathbb {P}\subset {\rm GL}_n$ such that
for some integers ![]() $a_{\mathcal {P}'}$. As the induced representation on the left-hand side is self-dual, so must
$a_{\mathcal {P}'}$. As the induced representation on the left-hand side is self-dual, so must ![]() $\sigma _\mathcal {P}$ be.
$\sigma _\mathcal {P}$ be.
It follows that we can identify ![]() $\mathcal {H}_G=\mathcal {H}_G(V,\lambda )$ with
$\mathcal {H}_G=\mathcal {H}_G(V,\lambda )$ with ![]() $\mathcal {H}_G(V,\lambda ^\vee )$. In particular, we obtain a canonical isomorphism
$\mathcal {H}_G(V,\lambda ^\vee )$. In particular, we obtain a canonical isomorphism ![]() $\mathcal {H}_G\cong \mathcal {H}_G^{\rm op}$.
$\mathcal {H}_G\cong \mathcal {H}_G^{\rm op}$.
Lemma 4.9 Let ![]() $\mathcal {P}$ be a partition. Then
$\mathcal {P}$ be a partition. Then ![]() $\check e_{\mathcal {P}}=e_{\mathcal {P}}$.
$\check e_{\mathcal {P}}=e_{\mathcal {P}}$.
Proof. The canonical isomorphism ![]() $\alpha$ allows us to identify
$\alpha$ allows us to identify ![]() ${\rm End}_C(V^\vee,V^\vee )$ with
${\rm End}_C(V^\vee,V^\vee )$ with ![]() ${\rm End}_C(V,V)$ and
${\rm End}_C(V,V)$ and ![]() $\mathcal {H}_G=\mathcal {H}(G,\lambda )$ with
$\mathcal {H}_G=\mathcal {H}(G,\lambda )$ with ![]() $\mathcal {H}(G,\lambda ^\vee )$. By definition
$\mathcal {H}(G,\lambda ^\vee )$. By definition ![]() $\check e_\mathcal {P}$ is the element
$\check e_\mathcal {P}$ is the element
under this identification. We calculate that
 \[ \check e_\mathcal{P}(g)=\begin{cases} 0, & g\notin K,\\ f_\mathcal{P}^\vee\circ (\lambda^\vee(k^{-1}))^\vee=f_\mathcal{P}^\vee\circ \lambda(k), & g\in K. \end{cases} \]
\[ \check e_\mathcal{P}(g)=\begin{cases} 0, & g\notin K,\\ f_\mathcal{P}^\vee\circ (\lambda^\vee(k^{-1}))^\vee=f_\mathcal{P}^\vee\circ \lambda(k), & g\in K. \end{cases} \]
Here ![]() $f_\mathcal {P}^\vee$ is the idempotent endomorphism of
$f_\mathcal {P}^\vee$ is the idempotent endomorphism of ![]() $V$ defined by the direct summand
$V$ defined by the direct summand ![]() $\Sigma _\mathcal {P}$. As the
$\Sigma _\mathcal {P}$. As the ![]() $\sigma _\mathcal {P}$ are self-dual the isomorphism
$\sigma _\mathcal {P}$ are self-dual the isomorphism ![]() $\alpha$ maps
$\alpha$ maps ![]() $\Sigma _{\mathcal {P}}$ to
$\Sigma _{\mathcal {P}}$ to ![]() $\Sigma ^\vee _{\mathcal {P}}$. Hence, we conclude that (under the identification
$\Sigma ^\vee _{\mathcal {P}}$. Hence, we conclude that (under the identification ![]() ${\rm End}_C(V^\vee,V^\vee )={\rm End}_C(V,V)$ using
${\rm End}_C(V^\vee,V^\vee )={\rm End}_C(V,V)$ using ![]() $\alpha$) the element
$\alpha$) the element ![]() $\check e_\mathcal {P}$ equals
$\check e_\mathcal {P}$ equals ![]() $e_\mathcal {P}$.
$e_\mathcal {P}$.
Recall that ![]() $\mathcal {H}_G$ contains the finite Hecke algebra
$\mathcal {H}_G$ contains the finite Hecke algebra
 \begin{align*}
\mathcal{H}_{G,0}=\mathcal{C}_c^\infty(I\backslash
K/I)&=\{f:\mathbb{B}(k)\backslash {\rm
GL}_n(k)/\mathbb{B}(k)\rightarrow C\}\\
&=\left\{f:K\rightarrow {\rm End}_CV\, \left|\!\begin{array}{c@{}}
f(k_1kk_2)=\lambda(k_1)\circ f(k)\circ \lambda(k_2)\\
\text{for all}\ k,k_1,k_2\in K \end{array}\right.\right\}\\
&={\rm End}_K(V) \end{align*}
\begin{align*}
\mathcal{H}_{G,0}=\mathcal{C}_c^\infty(I\backslash
K/I)&=\{f:\mathbb{B}(k)\backslash {\rm
GL}_n(k)/\mathbb{B}(k)\rightarrow C\}\\
&=\left\{f:K\rightarrow {\rm End}_CV\, \left|\!\begin{array}{c@{}}
f(k_1kk_2)=\lambda(k_1)\circ f(k)\circ \lambda(k_2)\\
\text{for all}\ k,k_1,k_2\in K \end{array}\right.\right\}\\
&={\rm End}_K(V) \end{align*}
as a subalgebra. This algebra contains the idempotent elements ![]() $e_\mathcal {P}$. Further, recall that for a parabolic subgroup
$e_\mathcal {P}$. Further, recall that for a parabolic subgroup ![]() $\mathbb {P}\subset \mathbb {G}$ containing
$\mathbb {P}\subset \mathbb {G}$ containing ![]() $\mathbb {B}$ we have an embedding
$\mathbb {B}$ we have an embedding ![]() $\mathcal {H}_M\hookrightarrow \mathcal {H}_G$ of Hecke algebras, where
$\mathcal {H}_M\hookrightarrow \mathcal {H}_G$ of Hecke algebras, where ![]() $M=\mathbb {M}(F)$ is the Levi of
$M=\mathbb {M}(F)$ is the Levi of ![]() $\mathbb {P}$. If
$\mathbb {P}$. If ![]() $\mathbb {P}=\mathbb {B}$ this gives an embedding
$\mathbb {P}=\mathbb {B}$ this gives an embedding
By [Reference Haines, Kottwitz and PrasadHKP10, Lemma 1.7.1] the morphism
induced by multiplication is an isomorphism of ![]() $C$-vector spaces.
$C$-vector spaces.
(i) The canonical inclusion
 $\mathcal {H}_T e_{G,{\rm st}}\subset \mathcal {H}_G e_{G,{\rm st}}$ is an equality. Moreover, this module is free of rank one with basis
$\mathcal {H}_T e_{G,{\rm st}}\subset \mathcal {H}_G e_{G,{\rm st}}$ is an equality. Moreover, this module is free of rank one with basis  $e_{G,{\rm st}}$ as an
$e_{G,{\rm st}}$ as an  $\mathcal {H}_T$-module.
$\mathcal {H}_T$-module.(ii) Let
 $\mathbb {P}\subset \mathbb {G}$ be a parabolic as above and let
$\mathbb {P}\subset \mathbb {G}$ be a parabolic as above and let  $M=\mathbb {M}(F)\subset G$ be the corresponding Levi subgroup. The isomorphism
of free
$M=\mathbb {M}(F)\subset G$ be the corresponding Levi subgroup. The isomorphism
of free \[ \mathcal{H}_Me_{M,{\rm st}}=\mathcal{H}_T e_{M,{\rm st}}\longrightarrow \mathcal{H}_Ge_{G,{\rm st}}=\mathcal{H}_Te_{G,{\rm st}} \]
\[ \mathcal{H}_Me_{M,{\rm st}}=\mathcal{H}_T e_{M,{\rm st}}\longrightarrow \mathcal{H}_Ge_{G,{\rm st}}=\mathcal{H}_Te_{G,{\rm st}} \]
 $\mathcal {H}_T$-modules of rank one defined by
$\mathcal {H}_T$-modules of rank one defined by  $e_{M,{\rm st}}\mapsto e_{G,{\rm st}}$ is an
$e_{M,{\rm st}}\mapsto e_{G,{\rm st}}$ is an  $\mathcal {H}_M$-module homomorphism.
$\mathcal {H}_M$-module homomorphism.
Proof. (i) It follows directly from (4.8) that ![]() $\mathcal {H}_Te_{G,{\rm st}}$ is free of rank one as an
$\mathcal {H}_Te_{G,{\rm st}}$ is free of rank one as an ![]() $\mathcal {H}_T$-module. Moreover, note that
$\mathcal {H}_T$-module. Moreover, note that
is a one-dimensional ![]() $C$-vector space. This implies that
$C$-vector space. This implies that ![]() $f\in \mathcal {H}_G$ can be written as the sum
$f\in \mathcal {H}_G$ can be written as the sum ![]() $f=f_0e_{G,{\rm st}} +f_1(1-e_{G,{\rm st}})$ with
$f=f_0e_{G,{\rm st}} +f_1(1-e_{G,{\rm st}})$ with ![]() $f_0\in \mathcal {H}_T$ and
$f_0\in \mathcal {H}_T$ and ![]() $f_1\in \mathcal {H}_G$. It follows that
$f_1\in \mathcal {H}_G$. It follows that
(ii) As the inclusion ![]() $\mathcal {H}_Te_{G,{\rm st}}\subset \mathcal {H}_Ge_{G,{\rm st}}$ is an equality, we also have an equality
$\mathcal {H}_Te_{G,{\rm st}}\subset \mathcal {H}_Ge_{G,{\rm st}}$ is an equality, we also have an equality ![]() $\mathcal {H}_Me_{G,{\rm st}}=\mathcal {H}_Ge_{G,{\rm st}}$. Therefore, it is enough to show that the
$\mathcal {H}_Me_{G,{\rm st}}=\mathcal {H}_Ge_{G,{\rm st}}$. Therefore, it is enough to show that the ![]() $\mathcal {H}_M$-module homomorphism
$\mathcal {H}_M$-module homomorphism
mapping ![]() $1$ to
$1$ to ![]() $e_{G,{\rm st}}$ factors through
$e_{G,{\rm st}}$ factors through ![]() $\mathcal {H}_M\rightarrow \mathcal {H}_Me_{M,{\rm st}}$. That is, we need to show
$\mathcal {H}_M\rightarrow \mathcal {H}_Me_{M,{\rm st}}$. That is, we need to show ![]() $(1-e_{M, {\rm st}})e_{G,{\rm st}}=0$ in
$(1-e_{M, {\rm st}})e_{G,{\rm st}}=0$ in ![]() $\mathcal {H}_G$. We can check this equality in the subalgebra
$\mathcal {H}_G$. We can check this equality in the subalgebra ![]() $\mathcal {H}_{G,0}$. Translating the claim back to representation theory, it comes down to the claim that
$\mathcal {H}_{G,0}$. Translating the claim back to representation theory, it comes down to the claim that
contains the direct summand ![]() ${\rm st}_G$, where
${\rm st}_G$, where ![]() $\mathbb {B}_M=\mathbb {B}\cap \mathbb {M}$ is a Borel in
$\mathbb {B}_M=\mathbb {B}\cap \mathbb {M}$ is a Borel in ![]() $\mathbb {M}$. This is true, as
$\mathbb {M}$. This is true, as ![]() ${\rm st}_G$ is the only constituent of the right-hand side that does not occur in
${\rm st}_G$ is the only constituent of the right-hand side that does not occur in ![]() ${\rm Ind}_{\mathbb {P}'(k)}^{{\rm GL}_n(k)}\mathbf {1}_{\mathbb {P}'(k)}$ for any parabolic
${\rm Ind}_{\mathbb {P}'(k)}^{{\rm GL}_n(k)}\mathbf {1}_{\mathbb {P}'(k)}$ for any parabolic ![]() $\mathbb {P}'$ strictly larger than
$\mathbb {P}'$ strictly larger than ![]() $\mathbb {B}$.
$\mathbb {B}$.
Corollary 4.11 Let ![]() $x=(\varphi _x,N_x)\in X_{\check G}$ with
$x=(\varphi _x,N_x)\in X_{\check G}$ with ![]() $\varphi _x$ regular semi-simple and let
$\varphi _x$ regular semi-simple and let ![]() $L$ be an extension of
$L$ be an extension of ![]() $k(x)$ containing all the eigenvalues of
$k(x)$ containing all the eigenvalues of ![]() $\varphi _x$. Then
$\varphi _x$. Then
and after extending scalars to ![]() $L$ its Jacquet module is given by
$L$ its Jacquet module is given by
where the sum is indexed by the ![]() $\varphi _x$-stable flags
$\varphi _x$-stable flags ![]() $\mathcal {F}$ of
$\mathcal {F}$ of ![]() $L^n$. Moreover, the kernel of the quotient map of
$L^n$. Moreover, the kernel of the quotient map of ![]() $\mathcal {H}_T$-modules
$\mathcal {H}_T$-modules
is ![]() $\mathcal {H}_G$-stable and the induced
$\mathcal {H}_G$-stable and the induced ![]() $\mathcal {H}_G$-module structure on the quotient identifies the right-hand side with the
$\mathcal {H}_G$-module structure on the quotient identifies the right-hand side with the ![]() $I$-invariants of (the scalar extension to
$I$-invariants of (the scalar extension to ![]() $L$ of) the quotient
$L$ of) the quotient ![]() ${\rm LL^{mod}}((\varphi _x,N_x)^\vee )^\vee$ in Lemma 4.7.
${\rm LL^{mod}}((\varphi _x,N_x)^\vee )^\vee$ in Lemma 4.7.
Proof. The first claim is a direct consequence of ![]() $(\operatorname {c-ind}_N^G\psi )_{[T,1]}\cong \operatorname {c-ind}_K^G{\rm st}_G$ and the identification
$(\operatorname {c-ind}_N^G\psi )_{[T,1]}\cong \operatorname {c-ind}_K^G{\rm st}_G$ and the identification
The claim on the Jacquet module follows from ![]() $\mathcal {H}_Ge_{G,{\rm st}}=\mathcal {H}_Te_{G,{\rm st}}$ and (3.6).
$\mathcal {H}_Ge_{G,{\rm st}}=\mathcal {H}_Te_{G,{\rm st}}$ and (3.6).
For the second part, note that the right-hand side in (4.9) is uniquely determined as an ![]() $\mathcal {H}_T$-module, as the characters
$\mathcal {H}_T$-module, as the characters ![]() ${\rm unr}_{\mathcal {F}}$ are pairwise distinct. Hence, it is enough to prove that the quotient
${\rm unr}_{\mathcal {F}}$ are pairwise distinct. Hence, it is enough to prove that the quotient
given by Lemma 4.7 induces this quotient map on the underlying ![]() $\mathcal {H}_T$-modules (and after extending scalars to
$\mathcal {H}_T$-modules (and after extending scalars to ![]() $L$). This is a consequence of the computation of
$L$). This is a consequence of the computation of ![]() $r^G_B({\rm LL^{mod}}((\varphi _x,N_x)^\vee )^\vee \otimes _{k(x)}L)$ (see Lemma 4.3).
$r^G_B({\rm LL^{mod}}((\varphi _x,N_x)^\vee )^\vee \otimes _{k(x)}L)$ (see Lemma 4.3).
We finish this subsection by recalling some easy facts about the passage from left to right modules over ![]() $\mathcal {H}_G$. Given a left
$\mathcal {H}_G$. Given a left ![]() $\mathcal {H}_G$-module
$\mathcal {H}_G$-module ![]() $\pi$, one can view
$\pi$, one can view ![]() $\pi$ as a right
$\pi$ as a right ![]() $\mathcal {H}_G$-module via the isomorphism
$\mathcal {H}_G$-module via the isomorphism ![]() $\mathcal {H}_G\cong \mathcal {H}_G^{\rm op}$. We write
$\mathcal {H}_G\cong \mathcal {H}_G^{\rm op}$. We write ![]() ${}^t\pi$ for this right module structure on
${}^t\pi$ for this right module structure on ![]() $\pi$.
$\pi$.
Lemma 4.12 Let ![]() $M\subset G$ be a Levi and let
$M\subset G$ be a Levi and let ![]() $\pi$ be a left
$\pi$ be a left ![]() $\mathcal {H}_M$-module. Then there is a canonical and functorial isomorphism of right
$\mathcal {H}_M$-module. Then there is a canonical and functorial isomorphism of right ![]() $\mathcal {H}_G$-modules
$\mathcal {H}_G$-modules
where the ![]() $\mathcal {H}_G$-module structure on the right-hand side is given by right multiplication.
$\mathcal {H}_G$-module structure on the right-hand side is given by right multiplication.
Proof. It is easily checked that ![]() $\varphi \otimes v\longmapsto v\otimes \check \varphi$ defines the desired isomorphism.
$\varphi \otimes v\longmapsto v\otimes \check \varphi$ defines the desired isomorphism.
Lemma 4.13 Let ![]() $\pi$ be an
$\pi$ be an ![]() $\mathcal {H}_G$-module and let
$\mathcal {H}_G$-module and let ![]() $e\in \mathcal {H}_G$ be an idempotent element.
$e\in \mathcal {H}_G$ be an idempotent element.
(i) There is a canonical equality of
 $\mathfrak {Z}$-modules
$\mathfrak {Z}$-modules
 \[ {\rm Hom}_{\mathcal{H}_G}(\mathcal{H}_Ge,\pi)=e\pi=e\mathcal{H}_G\otimes_{\mathcal{H}_G}\pi. \]
\[ {\rm Hom}_{\mathcal{H}_G}(\mathcal{H}_Ge,\pi)=e\pi=e\mathcal{H}_G\otimes_{\mathcal{H}_G}\pi. \]
(ii) There is a canonical identification
 ${}^t(\mathcal {H}_Ge)=\check e\mathcal {H}$ as
${}^t(\mathcal {H}_Ge)=\check e\mathcal {H}$ as  $\mathcal {H}_G$ right modules.
$\mathcal {H}_G$ right modules.(iii) Let
 $\mathcal {P}$ be a partition. Then
$\mathcal {P}$ be a partition. Then
 \[ {\rm Hom}_{\mathcal{H}_G}(\mathcal{H}_Ge_\mathcal{P},\pi)={}^t(\mathcal{H}_Ge_\mathcal{P})\otimes_{\mathcal{H}_G}\pi. \]
\[ {\rm Hom}_{\mathcal{H}_G}(\mathcal{H}_Ge_\mathcal{P},\pi)={}^t(\mathcal{H}_Ge_\mathcal{P})\otimes_{\mathcal{H}_G}\pi. \]
(iv) For two partitions
 $\mathcal {P},\mathcal {P}'$ we have
$\mathcal {P},\mathcal {P}'$ we have
 \[ e_{\mathcal{P}}\mathcal{H}_Ge_{\mathcal{P}'}\cong \mathfrak{Z}^{m_{\mathcal{P}}^2m_{\mathcal{P}'}^2}. \]
\[ e_{\mathcal{P}}\mathcal{H}_Ge_{\mathcal{P}'}\cong \mathfrak{Z}^{m_{\mathcal{P}}^2m_{\mathcal{P}'}^2}. \]
Proof. Part (i) and (ii) are obvious, and (iii) is a direct consequence of (i), (ii) and ![]() $\check e_{\mathcal {P}}=e_{\mathcal {P}}$. Finally, we find
$\check e_{\mathcal {P}}=e_{\mathcal {P}}$. Finally, we find
 \begin{align*} e_{\mathcal{P}}\mathcal{H}_Ge_{\mathcal{P}'}={\rm Hom}_{\mathcal{H}_G} (\mathcal{H}_G e_{\mathcal{P}},\mathcal{H}_Ge_{\mathcal{P}'})&={\rm Hom}_G(\operatorname{c-ind}_K^G\Sigma_\mathcal{P}, \operatorname{c-ind}_K^G\Sigma_{\mathcal{P}'})\\ &={\rm Hom}_G(\operatorname{c-ind}_K^G\sigma_\mathcal{P},\operatorname{c-ind}_K^G\sigma_{\mathcal{P}'})^{m_{\mathcal{P}}m_{\mathcal{P}'}}. \end{align*}
\begin{align*} e_{\mathcal{P}}\mathcal{H}_Ge_{\mathcal{P}'}={\rm Hom}_{\mathcal{H}_G} (\mathcal{H}_G e_{\mathcal{P}},\mathcal{H}_Ge_{\mathcal{P}'})&={\rm Hom}_G(\operatorname{c-ind}_K^G\Sigma_\mathcal{P}, \operatorname{c-ind}_K^G\Sigma_{\mathcal{P}'})\\ &={\rm Hom}_G(\operatorname{c-ind}_K^G\sigma_\mathcal{P},\operatorname{c-ind}_K^G\sigma_{\mathcal{P}'})^{m_{\mathcal{P}}m_{\mathcal{P}'}}. \end{align*}
Now (iv) follows from [Reference PyvovarovPyv20a, Theorem 1.4].
4.4 The Hecke module of the interpolating family
In § 4.2 we constructed a family of ![]() $G$-representations
$G$-representations ![]() $\mathcal {V}_G$ on the stack
$\mathcal {V}_G$ on the stack ![]() $[X_{\check G}/\check G]$. Let
$[X_{\check G}/\check G]$. Let
denote the corresponding module over the Iwahori–Hecke algebra. We write ![]() $\tilde {\mathcal {M}}_G$ for the corresponding
$\tilde {\mathcal {M}}_G$ for the corresponding ![]() $\check G$-equivariant sheaf of
$\check G$-equivariant sheaf of ![]() $\mathcal {O}_{X_{\check G}}\otimes _{\mathfrak {Z}}\mathcal {H}_G$-modules on
$\mathcal {O}_{X_{\check G}}\otimes _{\mathfrak {Z}}\mathcal {H}_G$-modules on ![]() $X_{\check G}$.
$X_{\check G}$.
We write ![]() $A_{\check G}$ for the coordinate ring of
$A_{\check G}$ for the coordinate ring of ![]() $X_{\check G}$. Similarly, given a Levi subgroup
$X_{\check G}$. Similarly, given a Levi subgroup ![]() $\mathbb {M}\subset \mathbb {G}$, we write
$\mathbb {M}\subset \mathbb {G}$, we write ![]() $A_{\check M}$ for the coordinate ring of
$A_{\check M}$ for the coordinate ring of ![]() $X_{\check M}$. Recall that we have embeddings
$X_{\check M}$. Recall that we have embeddings ![]() $\mathcal {H}_M\hookrightarrow \mathcal {H}_G$ and a canonical isomorphism
$\mathcal {H}_M\hookrightarrow \mathcal {H}_G$ and a canonical isomorphism ![]() $\mathcal {H}_T=\mathfrak {Z}_T\cong A_{\check T}$.
$\mathcal {H}_T=\mathfrak {Z}_T\cong A_{\check T}$.
Recall the following diagram of ![]() $C$-schemes from § 2:
$C$-schemes from § 2:

Assuming Conjecture 2.17, the complex
is concentrated in degree zero and, as ![]() $\beta '$ is affine, so is
$\beta '$ is affine, so is ![]() $R\tilde \gamma _\ast \mathcal {O}_{\tilde {\mathbf {X}}_{\check B}}$. Hence, the formulation of the following conjecture makes sense.
$R\tilde \gamma _\ast \mathcal {O}_{\tilde {\mathbf {X}}_{\check B}}$. Hence, the formulation of the following conjecture makes sense.
Conjecture 4.14 Let ![]() $\mathbb {G}={\rm GL}_n$ and assume Conjecture 2.17. Then the canonical map
$\mathbb {G}={\rm GL}_n$ and assume Conjecture 2.17. Then the canonical map
is a surjection.
Note that Conjecture 4.14 would imply that we have a canonical surjection
Remark 4.15 We point out that Conjecture 4.14 is a conjecture for the group ![]() ${\rm GL}_n$ and will fail for other groups. In fact it already fails for
${\rm GL}_n$ and will fail for other groups. In fact it already fails for ![]() ${\rm SL}_2$ and its failure seems to be related to the existence of non-trivial L-packets. We refer to Example 4.33 below for a discussion of this point.
${\rm SL}_2$ and its failure seems to be related to the existence of non-trivial L-packets. We refer to Example 4.33 below for a discussion of this point.
The restriction of the above diagram to the regular locus yields the following diagram.

Theorem 4.16 Conjecture 4.14 is true over the regular locus. That is, the canonical morphism
is a surjection. Moreover, the restriction of the induced surjection (4.10) to the regular locus and the identification
equips ![]() $R\tilde \beta _{B,\ast }\mathcal {O}_{\tilde X_{\check B}^{\rm reg}}$ with the structure of an
$R\tilde \beta _{B,\ast }\mathcal {O}_{\tilde X_{\check B}^{\rm reg}}$ with the structure of an ![]() $\mathcal {O}_{X_{\check G}^{\rm reg}}\otimes _{\mathfrak {Z}}\mathcal {H}_G$-module that identifies this sheaf with the restriction
$\mathcal {O}_{X_{\check G}^{\rm reg}}\otimes _{\mathfrak {Z}}\mathcal {H}_G$-module that identifies this sheaf with the restriction ![]() $\tilde {\mathcal {M}}_G|_{X_{\check G}^{\rm reg}}$ of the Hecke module defined by the Emerton–Helm family.
$\tilde {\mathcal {M}}_G|_{X_{\check G}^{\rm reg}}$ of the Hecke module defined by the Emerton–Helm family.
Remark 4.17 We point out that proving Conjecture 4.14 would automatically imply that the identification of ![]() $R\tilde \beta _{B,\ast }\mathcal {O}_{\tilde {\mathbf {X}}_{\check B}}$ with the Hecke module underlying the Emerton–Helm family holds true without restricting to the regular locus.
$R\tilde \beta _{B,\ast }\mathcal {O}_{\tilde {\mathbf {X}}_{\check B}}$ with the Hecke module underlying the Emerton–Helm family holds true without restricting to the regular locus.
Lemma 4.18 The morphism
is a closed immersion.
Proof. Clearly ![]() $\gamma$ is a finite morphism, by the very definition of the regular locus. Hence, it is enough to show that
$\gamma$ is a finite morphism, by the very definition of the regular locus. Hence, it is enough to show that ![]() $\gamma$ induces an injection on
$\gamma$ induces an injection on ![]() $k$-valued points, for algebraically closed fields
$k$-valued points, for algebraically closed fields ![]() $k$, and a surjection on complete local rings.
$k$, and a surjection on complete local rings.
Let ![]() $k$ be an algebraically closed extension of
$k$ be an algebraically closed extension of ![]() $C$ and let
$C$ and let ![]() $(A,\mathfrak {m})$ be a local Artinian
$(A,\mathfrak {m})$ be a local Artinian ![]() $C$-algebra with residue field
$C$-algebra with residue field ![]() $k$. Let
$k$. Let ![]() $(\varphi,N)\in X_{\check G}^{\rm reg}(A)$ and let
$(\varphi,N)\in X_{\check G}^{\rm reg}(A)$ and let ![]() $\lambda _1,\ldots,\lambda _n\in A$. Then we have to show that there is at most one complete flag
$\lambda _1,\ldots,\lambda _n\in A$. Then we have to show that there is at most one complete flag ![]() $\mathcal {F}_\bullet$ of
$\mathcal {F}_\bullet$ of ![]() $A^n$ stable under
$A^n$ stable under ![]() $\varphi$ and
$\varphi$ and ![]() $N$ such that
$N$ such that ![]() $\varphi$ acts on
$\varphi$ acts on ![]() $\mathcal {F}_i/\mathcal {F}_{i-1}$ by multiplication with
$\mathcal {F}_i/\mathcal {F}_{i-1}$ by multiplication with ![]() $\lambda _i$.
$\lambda _i$.
Assume first ![]() $A=k$. We prove the claim by induction on
$A=k$. We prove the claim by induction on ![]() $n$. The case
$n$. The case ![]() $n=1$ is trivial. Assume the claim is true for
$n=1$ is trivial. Assume the claim is true for ![]() $n-1$. Then it is enough to show that there is a unique
$n-1$. Then it is enough to show that there is a unique ![]() $(\varphi,N)$-stable line
$(\varphi,N)$-stable line ![]() $\mathcal {F}_1$ in
$\mathcal {F}_1$ in ![]() $k^n$ on which
$k^n$ on which ![]() $\varphi$ acts by multiplication with
$\varphi$ acts by multiplication with ![]() $\lambda _1$. Obviously this forces
$\lambda _1$. Obviously this forces ![]() $\mathcal {F}\subset \ker N$ and we need to show that the
$\mathcal {F}\subset \ker N$ and we need to show that the ![]() $\varphi$-eigenspace in
$\varphi$-eigenspace in ![]() $\ker N$ of eigenvalue
$\ker N$ of eigenvalue ![]() $\lambda _1$ is one-dimensional. However, if this is not the case then there are infinitely many pairwise distinct
$\lambda _1$ is one-dimensional. However, if this is not the case then there are infinitely many pairwise distinct ![]() $(\varphi,N)$-stable lines in
$(\varphi,N)$-stable lines in ![]() $k^n$, and each can be completed to a complete
$k^n$, and each can be completed to a complete ![]() $(\varphi,N)$-stable flag. This contradicts the regularity of
$(\varphi,N)$-stable flag. This contradicts the regularity of ![]() $(\varphi,N)$.
$(\varphi,N)$.
Now assume that ![]() $(A,\mathfrak {m})$ is a general Artinian
$(A,\mathfrak {m})$ is a general Artinian ![]() $C$-algebra with residue field
$C$-algebra with residue field ![]() $k$. Again it suffices to show that there is a unique
$k$. Again it suffices to show that there is a unique ![]() $(\varphi,N)$-stable
$(\varphi,N)$-stable ![]() $A$-line in
$A$-line in ![]() $A^n$, such that the quotient of
$A^n$, such that the quotient of ![]() $A^n$ by this line is free, on which
$A^n$ by this line is free, on which ![]() $\varphi$ acts as multiplication by
$\varphi$ acts as multiplication by ![]() $\lambda _1$. By induction on the length of
$\lambda _1$. By induction on the length of ![]() $A$ we can reduce to the following situation: there exists
$A$ we can reduce to the following situation: there exists ![]() $f\in A$ such that
$f\in A$ such that ![]() $\mathfrak {m}f=0$, and if
$\mathfrak {m}f=0$, and if ![]() $A'=A/(f)$ and
$A'=A/(f)$ and ![]() $(\varphi ',N')$ is the image of
$(\varphi ',N')$ is the image of ![]() $(\varphi,N)$ in
$(\varphi,N)$ in ![]() $X_{\check G}^{\rm reg}(A')$, then there is a unique
$X_{\check G}^{\rm reg}(A')$, then there is a unique ![]() $(\varphi ',N')$ stable
$(\varphi ',N')$ stable ![]() $A'$-line in
$A'$-line in ![]() $A'^n$ on which
$A'^n$ on which ![]() $\varphi '$ acts by multiplication with
$\varphi '$ acts by multiplication with ![]() $\lambda _1\ {\rm mod}\,(f)$. Let
$\lambda _1\ {\rm mod}\,(f)$. Let ![]() $(\bar \varphi,\bar N)\in X_{\check G}^{\rm reg}(k)$ denote the reduction of
$(\bar \varphi,\bar N)\in X_{\check G}^{\rm reg}(k)$ denote the reduction of ![]() $(\varphi,N)$ modulo
$(\varphi,N)$ modulo ![]() $\mathfrak {m}$ and let
$\mathfrak {m}$ and let ![]() $\bar \lambda _1\in k$ denote the reduction of
$\bar \lambda _1\in k$ denote the reduction of ![]() $\lambda _1$. Then multiplication by
$\lambda _1$. Then multiplication by ![]() $f$ induces an embedding of
$f$ induces an embedding of ![]() $k^n\hookrightarrow A^n$ of
$k^n\hookrightarrow A^n$ of ![]() $(\varphi,N)$-modules with cokernel
$(\varphi,N)$-modules with cokernel ![]() $A'^n$. Assume that
$A'^n$. Assume that ![]() $\mathcal {F}_1=Ae_1$ and
$\mathcal {F}_1=Ae_1$ and ![]() $\mathcal {F}'_1=Ae'_1$ are two
$\mathcal {F}'_1=Ae'_1$ are two ![]() $(\varphi,N)$-stable
$(\varphi,N)$-stable ![]() $A$-lines on which
$A$-lines on which ![]() $\varphi$ acts by multiplication with
$\varphi$ acts by multiplication with ![]() $\lambda _1$. Then the assumption implies
$\lambda _1$. Then the assumption implies ![]() $e'_1=\alpha e_1+fv$ for some
$e'_1=\alpha e_1+fv$ for some ![]() $\alpha \in A^\times$ and
$\alpha \in A^\times$ and ![]() $v\in k^n$. Let
$v\in k^n$. Let ![]() $\bar e_1\in k^n$ denote the reduction of
$\bar e_1\in k^n$ denote the reduction of ![]() $e_1$ modulo
$e_1$ modulo ![]() $\mathfrak {m}$, then it remains to show
$\mathfrak {m}$, then it remains to show ![]() $v\in k\bar e_1$. As
$v\in k\bar e_1$. As ![]() $\varphi (e_1)=\lambda _1 e_1$ and
$\varphi (e_1)=\lambda _1 e_1$ and ![]() $\varphi (e'_1)=\lambda _1 e'_1$ we deduce
$\varphi (e'_1)=\lambda _1 e'_1$ we deduce ![]() $\bar \varphi (v)=\bar \lambda _1v$. The discussion of the case of an algebraically closed field
$\bar \varphi (v)=\bar \lambda _1v$. The discussion of the case of an algebraically closed field ![]() $k$ above implies that it is enough to prove that
$k$ above implies that it is enough to prove that ![]() $v\in \ker \bar N$. However, we assume that
$v\in \ker \bar N$. However, we assume that ![]() $\mathcal {F}_1$ and
$\mathcal {F}_1$ and ![]() $\mathcal {F}'_1$ are defined by points
$\mathcal {F}'_1$ are defined by points ![]() $(\varphi,N,\mathcal {F}_\bullet ), (\varphi,N,\mathcal {F}'_\bullet )\in X_{\check G}^{\rm reg}(A)$. As
$(\varphi,N,\mathcal {F}_\bullet ), (\varphi,N,\mathcal {F}'_\bullet )\in X_{\check G}^{\rm reg}(A)$. As ![]() $X_{\check G}^{\rm reg}$ is reduced by Lemma 2.7 and as
$X_{\check G}^{\rm reg}$ is reduced by Lemma 2.7 and as ![]() $N$ is nilpotent we deduce that
$N$ is nilpotent we deduce that ![]() $N(\mathcal {F}_1)=N(\mathcal {F}'_1)=0$ and hence
$N(\mathcal {F}_1)=N(\mathcal {F}'_1)=0$ and hence ![]() $N(fv)=0$, which implies
$N(fv)=0$, which implies ![]() $\bar N(v)=0$.
$\bar N(v)=0$.
We use the lemma to identify ![]() $\tilde X_{\check B}^{\rm reg}$ with a closed subscheme
$\tilde X_{\check B}^{\rm reg}$ with a closed subscheme ![]() $Y_{\check G}^{\rm reg}$ of
$Y_{\check G}^{\rm reg}$ of ![]() $X_{\check G}^{\rm reg}\times _{\check T/W}\check T$. We denote by
$X_{\check G}^{\rm reg}\times _{\check T/W}\check T$. We denote by
the closure of ![]() $Y_{\check G}^{\rm reg}$ equipped with its canonical scheme structure (which is the reduced structure, as
$Y_{\check G}^{\rm reg}$ equipped with its canonical scheme structure (which is the reduced structure, as ![]() $\tilde X_{\check B}^{\rm reg}$ is reduced). Let us write
$\tilde X_{\check B}^{\rm reg}$ is reduced). Let us write ![]() $\tilde A_{\check G}$ for the corresponding quotient of
$\tilde A_{\check G}$ for the corresponding quotient of ![]() $A_{\check G}\otimes _{\mathfrak {Z}}A_{\check T}$ and
$A_{\check G}\otimes _{\mathfrak {Z}}A_{\check T}$ and ![]() $\beta :Y_{\check G}\rightarrow X_{\check G}$ for the canonical projection.
$\beta :Y_{\check G}\rightarrow X_{\check G}$ for the canonical projection.
We can use Lemma 4.10 to equip
with an ![]() $\mathcal {H}_G$-module structure.
$\mathcal {H}_G$-module structure.
(i) The kernel of the canonical morphism
 $A_{\check G}\otimes _{\mathfrak {Z}}A_{\check T}\rightarrow \tilde A_{\check G}$ is stable under the action of
$A_{\check G}\otimes _{\mathfrak {Z}}A_{\check T}\rightarrow \tilde A_{\check G}$ is stable under the action of  $\mathcal {H}_G$.
$\mathcal {H}_G$.(ii) There is a canonical isomorphism
of \[ \tilde{\mathcal{M}}_G\cong \beta_\ast \mathcal{O}_{Y_{\check G}} \]
\[ \tilde{\mathcal{M}}_G\cong \beta_\ast \mathcal{O}_{Y_{\check G}} \]
 $\check G$-equivariant
$\check G$-equivariant  $\mathcal {O}_{X_{\check G}}\otimes _{\mathfrak {Z}}\mathcal {H}_G$-modules.
$\mathcal {O}_{X_{\check G}}\otimes _{\mathfrak {Z}}\mathcal {H}_G$-modules.
Proof. (i) By Lemmas 2.5 and 2.7 the scheme ![]() $Y_{\check G}$ is reduced and every irreducible component of
$Y_{\check G}$ is reduced and every irreducible component of ![]() $Y_{\check G}$ dominates an irreducible component of
$Y_{\check G}$ dominates an irreducible component of ![]() $X_{\check G}$. In particular, the canonical morphism
$X_{\check G}$. In particular, the canonical morphism
is an injection. Here the product runs over all generic points ![]() $\eta$ of
$\eta$ of ![]() $X_{\check G}$. It is therefore enough to prove that for all generic points
$X_{\check G}$. It is therefore enough to prove that for all generic points ![]() $\eta$ of
$\eta$ of ![]() $X_{\check G}$ the kernel of the canonical map
$X_{\check G}$ the kernel of the canonical map
is stable under the ![]() $\mathcal {H}_G$-action. This follows from Corollary 4.11 applied to the generic point
$\mathcal {H}_G$-action. This follows from Corollary 4.11 applied to the generic point ![]() $\eta =(\varphi _\eta,N_\eta )$.
$\eta =(\varphi _\eta,N_\eta )$.
(ii) Consider the diagram

where the left vertical arrow comes from the identification of
and the right vertical arrow comes from the identification of the Jacquet module of ![]() ${\rm LL}(\varphi _\eta,N_\eta )$ in Corollary 4.11. By construction the diagram is a commutative diagram of
${\rm LL}(\varphi _\eta,N_\eta )$ in Corollary 4.11. By construction the diagram is a commutative diagram of ![]() $A_{\check G}\otimes _{\mathfrak {Z}}\mathcal {H}_{\check G}$-modules; moreover, all morphisms are compatible with the
$A_{\check G}\otimes _{\mathfrak {Z}}\mathcal {H}_{\check G}$-modules; moreover, all morphisms are compatible with the ![]() $\check G$-action. Hence, these morphisms induce a canonical isomorphism
$\check G$-action. Hence, these morphisms induce a canonical isomorphism
as claimed.
As a consequence we can easily deduce Conjecture 4.8 for regular semi-simple points. We refer to point (d) in § 4.7 for a discussion of non-regular points.
Corollary 4.20 Let ![]() $x=(\varphi,N)\in X_{\check G}$ with
$x=(\varphi,N)\in X_{\check G}$ with ![]() $\varphi$ regular semi-simple. Then
$\varphi$ regular semi-simple. Then
Proof. It follows from the proof of Proposition 4.19 that
is a surjection of ![]() $\mathcal {H}_T\otimes k(x)$-modules. The claim now follows from Corollary 4.11.
$\mathcal {H}_T\otimes k(x)$-modules. The claim now follows from Corollary 4.11.
The module of ![]() $I$-invariants in the family of smooth representation over
$I$-invariants in the family of smooth representation over ![]() $\ell$-adic deformation rings proposed by Emerton and Helm [Reference Emerton and HelmEH14] (and constructed by Helm in [Reference HelmHel16]) is expected to have a close relation with patched modules in the Taylor–Wiles method (for Iwahori level at
$\ell$-adic deformation rings proposed by Emerton and Helm [Reference Emerton and HelmEH14] (and constructed by Helm in [Reference HelmHel16]) is expected to have a close relation with patched modules in the Taylor–Wiles method (for Iwahori level at ![]() $p$). In fact the Taylor–Wiles patching modules automatically produces maximal Cohen–Macaulay modules (which are in fact self-dual for Grothendieck–Serre duality). The family defined in [Reference HelmHel16] is related to the family
$p$). In fact the Taylor–Wiles patching modules automatically produces maximal Cohen–Macaulay modules (which are in fact self-dual for Grothendieck–Serre duality). The family defined in [Reference HelmHel16] is related to the family ![]() $\mathcal {V}_G$ by the twist with
$\mathcal {V}_G$ by the twist with ![]() $|{\rm det}|^{-(n-1)/2}$ and by some flat base changes. This motivates the following conjecture which also would be a direct consequence of Conjecture 4.14 and the self-duality statement in Conjecture 2.17
$|{\rm det}|^{-(n-1)/2}$ and by some flat base changes. This motivates the following conjecture which also would be a direct consequence of Conjecture 4.14 and the self-duality statement in Conjecture 2.17
Conjecture 4.21 The Hecke module ![]() $\tilde {\mathcal {M}}_G=(\tilde {\mathcal {V}}_G)^I$ underlying the Emerton–Helm family
$\tilde {\mathcal {M}}_G=(\tilde {\mathcal {V}}_G)^I$ underlying the Emerton–Helm family ![]() $\tilde {\mathcal {V}}_G$ on
$\tilde {\mathcal {V}}_G$ on ![]() $X_{\check G}$ is a Cohen–Macaulay module over
$X_{\check G}$ is a Cohen–Macaulay module over ![]() $\mathcal {O}_{X_{\check G}}$.
$\mathcal {O}_{X_{\check G}}$.
Remark 4.22 One deduces easily from Proposition 4.19 that ![]() $\tilde {\mathcal {M}}_G$ cannot be flat as an
$\tilde {\mathcal {M}}_G$ cannot be flat as an ![]() $\mathcal {O}_{X_{\check G}}$-module. On the other hand, as explained above, the family
$\mathcal {O}_{X_{\check G}}$-module. On the other hand, as explained above, the family ![]() $\tilde {\mathcal {M}}_G$ should have some relation with patching modules and hence should satisfy some local-global compatibility with the cohomology of certain locally symmetric spaces. We do not give a very precise formulation of this here, but it would include the (derived) base change to a global Galois deformation ring. In the neighborhood of generic L-parameters there should be no obstruction for this base change to sit in a single cohomological degree. This motivates the following observation.
$\tilde {\mathcal {M}}_G$ should have some relation with patching modules and hence should satisfy some local-global compatibility with the cohomology of certain locally symmetric spaces. We do not give a very precise formulation of this here, but it would include the (derived) base change to a global Galois deformation ring. In the neighborhood of generic L-parameters there should be no obstruction for this base change to sit in a single cohomological degree. This motivates the following observation.
Corollary 4.23 Let ![]() $x=(\varphi,N)\in X_{\check G}^{\rm reg}$ such that the
$x=(\varphi,N)\in X_{\check G}^{\rm reg}$ such that the ![]() $\check G$-conjugacy class of
$\check G$-conjugacy class of ![]() $(\varphi,N)$ is a generic
$(\varphi,N)$ is a generic ![]() $L$-parameter. Then
$L$-parameter. Then ![]() $\tilde {\mathcal {M}}_G$ is locally free (as an
$\tilde {\mathcal {M}}_G$ is locally free (as an ![]() $\mathcal {O}_{X_{\check G}}$-module) in a neighborhood of
$\mathcal {O}_{X_{\check G}}$-module) in a neighborhood of ![]() $x$.
$x$.
Proof. As a maximal Cohen–Macaulay module over a regular local ring is automatically free, this follows from Remark 2.23 and the identification of ![]() $\tilde {\mathcal {M}}_G|_{X_{\check G}^{\rm reg}}$ above.
$\tilde {\mathcal {M}}_G|_{X_{\check G}^{\rm reg}}$ above.
4.5 The main conjecture in the regular case
After restricting to the regular case we give a candidate for the functor ![]() $R_G^\psi$ in Conjecture 3.2, as well as functors
$R_G^\psi$ in Conjecture 3.2, as well as functors ![]() $R_M^{\psi _M}$ for all (standard) Levi subgroups, and prove compatibility with parabolic induction. As in the case of
$R_M^{\psi _M}$ for all (standard) Levi subgroups, and prove compatibility with parabolic induction. As in the case of ![]() ${\rm GL}_n$ the choice of
${\rm GL}_n$ the choice of ![]() $(\mathbb {B},\psi )$ is unique up to conjugation, we will always omit the superscript
$(\mathbb {B},\psi )$ is unique up to conjugation, we will always omit the superscript ![]() $\psi$ from the notation. By abuse of notation we will also use the symbols
$\psi$ from the notation. By abuse of notation we will also use the symbols ![]() $\iota _P^G(-)$ and
$\iota _P^G(-)$ and ![]() $\iota _{\overline {P}}^G(-)$ to denote the functors on Hecke modules corresponding to parabolic induction (3.5).
$\iota _{\overline {P}}^G(-)$ to denote the functors on Hecke modules corresponding to parabolic induction (3.5).
For a standard Levi subgroup ![]() $\prod _{i=1}^s \operatorname {GL}_{r_i}=\mathbb {M}\subset \mathbb {G}=\operatorname {GL}_n$ we write
$\prod _{i=1}^s \operatorname {GL}_{r_i}=\mathbb {M}\subset \mathbb {G}=\operatorname {GL}_n$ we write ![]() $\tilde {\mathcal {M}}_M$ for the tensor product of the pullbacks of the
$\tilde {\mathcal {M}}_M$ for the tensor product of the pullbacks of the ![]() $\tilde {\mathcal {M}}_{\operatorname {GL}_{r_i}(F)}$ on
$\tilde {\mathcal {M}}_{\operatorname {GL}_{r_i}(F)}$ on ![]() $X_{\operatorname {GL}_{r_i}}$ to
$X_{\operatorname {GL}_{r_i}}$ to ![]() $X_{\check M}=\prod _{i=1}^s X_{\operatorname {GL}_{r_i}}$. This is an
$X_{\check M}=\prod _{i=1}^s X_{\operatorname {GL}_{r_i}}$. This is an ![]() $\check M$-equivariant sheaf of
$\check M$-equivariant sheaf of ![]() $\mathcal {O}_{X_{\check M}}\otimes _{\mathfrak {Z}_M}\mathcal {H}_M$-modules, and again we write
$\mathcal {O}_{X_{\check M}}\otimes _{\mathfrak {Z}_M}\mathcal {H}_M$-modules, and again we write ![]() $\mathcal {M}_M$ for the sheaf on
$\mathcal {M}_M$ for the sheaf on ![]() $[X_{\check M}/\check M]$ defined by
$[X_{\check M}/\check M]$ defined by ![]() $\tilde {\mathcal {M}}_M$. We define the functor
$\tilde {\mathcal {M}}_M$. We define the functor
 \begin{equation} \begin{aligned} R_M:{\bf D}^+(\mathcal{H}_M\text{-mod}) & \longrightarrow {\bf D}^+_{\rm QCoh}([X_{\check M}/\check M])\\ \pi^\bullet & \longmapsto {}^t\pi^\bullet\otimes^L_{\mathcal{H}_M}\mathcal{M}_M. \end{aligned} \end{equation}
\begin{equation} \begin{aligned} R_M:{\bf D}^+(\mathcal{H}_M\text{-mod}) & \longrightarrow {\bf D}^+_{\rm QCoh}([X_{\check M}/\check M])\\ \pi^\bullet & \longmapsto {}^t\pi^\bullet\otimes^L_{\mathcal{H}_M}\mathcal{M}_M. \end{aligned} \end{equation}
The derived tensor product in the formula can be defined for objects ![]() $\pi ^\bullet \in {\bf D}^+(\mathcal {H}_M\text {-mod})$ that are bounded above using finite projective resolutions (recall that
$\pi ^\bullet \in {\bf D}^+(\mathcal {H}_M\text {-mod})$ that are bounded above using finite projective resolutions (recall that ![]() $\mathcal {H}_M$ has finite global dimension). In general an object
$\mathcal {H}_M$ has finite global dimension). In general an object ![]() $\pi ^\bullet \in {\bf D}^+(\mathcal {H}_M\text {-mod})$ can be written as the direct limit of its truncations
$\pi ^\bullet \in {\bf D}^+(\mathcal {H}_M\text {-mod})$ can be written as the direct limit of its truncations
and we can define
Note that by definition ![]() $R_M$ preserves the truncation
$R_M$ preserves the truncation ![]() $\tau _{< m}$.
$\tau _{< m}$.
We will write ![]() $R_M^{\rm reg}$ for the composition of
$R_M^{\rm reg}$ for the composition of ![]() $R_M$ with the restriction to the regular locus
$R_M$ with the restriction to the regular locus ![]() $[X_{\check M}^{\rm reg}/\check M]\subset [X_{\check M}/\check M]$. Obviously the functors
$[X_{\check M}^{\rm reg}/\check M]\subset [X_{\check M}/\check M]$. Obviously the functors ![]() $R_M$ and
$R_M$ and ![]() $R_M^{\rm reg}$ are
$R_M^{\rm reg}$ are ![]() $\mathfrak {Z}_M$-linear.
$\mathfrak {Z}_M$-linear.
We restrict ourselves to the regular case. In order to have a compatible choice of the ![]() $\mathcal {M}_M$ (which are a priori only defined up to isomorphism) for various Levi subgroups of
$\mathcal {M}_M$ (which are a priori only defined up to isomorphism) for various Levi subgroups of ![]() $\operatorname {GL}_n$, let us set
$\operatorname {GL}_n$, let us set
where ![]() $B_M=B\cap M\subset M$ is a Borel and
$B_M=B\cap M\subset M$ is a Borel and ![]() $\beta _{B_M}$ is the restriction of the canonical projection
$\beta _{B_M}$ is the restriction of the canonical projection ![]() $[X_{\check B}/\check B]\rightarrow [X_{\check G}/\check G]$ to the regular locus. By abuse of notation we drop the restriction to the regular locus in the notation and just write
$[X_{\check B}/\check B]\rightarrow [X_{\check G}/\check G]$ to the regular locus. By abuse of notation we drop the restriction to the regular locus in the notation and just write ![]() $\mathcal {M}_M$ instead of
$\mathcal {M}_M$ instead of ![]() $\mathcal {M}_M^{\rm reg}$. We now use Proposition 4.19 to define the
$\mathcal {M}_M^{\rm reg}$. We now use Proposition 4.19 to define the ![]() $\mathcal {H}_M$-module structure on
$\mathcal {H}_M$-module structure on ![]() $\mathcal {M}_M$, that is, we let
$\mathcal {M}_M$, that is, we let ![]() $\mathcal {H}_M$ act on
$\mathcal {H}_M$ act on
by letting it act on ![]() $A_{\check T}=\mathcal {H}_T\cong \mathcal {H}_Me_{M,{\rm st}}$ (the fact that this
$A_{\check T}=\mathcal {H}_T\cong \mathcal {H}_Me_{M,{\rm st}}$ (the fact that this ![]() $\mathcal {H}_M$-action extends to the quotient is the content of Proposition 4.19).
$\mathcal {H}_M$-action extends to the quotient is the content of Proposition 4.19).
Let ![]() $\mathbb {P}_1\subset \mathbb {P}_2$ be parabolic subgroups containing
$\mathbb {P}_1\subset \mathbb {P}_2$ be parabolic subgroups containing ![]() $\mathbb {B}$ with Levi quotients
$\mathbb {B}$ with Levi quotients ![]() $\mathbb {M}_1$ and
$\mathbb {M}_1$ and ![]() $\mathbb {M}_2$ and write
$\mathbb {M}_2$ and write ![]() $\mathbb {P}_{12}$ for the image of
$\mathbb {P}_{12}$ for the image of ![]() $\mathbb {P}_1$ in
$\mathbb {P}_1$ in ![]() $\mathbb {M}_2$. We will define a natural
$\mathbb {M}_2$. We will define a natural ![]() $\mathfrak {Z}_{M_2}$-linear transformation
$\mathfrak {Z}_{M_2}$-linear transformation
where ![]() $\alpha _{12}$ and
$\alpha _{12}$ and ![]() $\beta _{12}$ are the morphisms in the following diagram.
$\beta _{12}$ are the morphisms in the following diagram.

Note that the square on the right-hand side is cartesian and Tor-independent by Lemma 2.9 and Corollary 2.11.
Let ![]() $\pi$ be a complex of
$\pi$ be a complex of ![]() $\mathcal {H}_{M_1}$-modules. Giving
$\mathcal {H}_{M_1}$-modules. Giving ![]() $\xi _{P_1}^{P_2}(\pi )$ is equivalent to defining its adjoint morphism
$\xi _{P_1}^{P_2}(\pi )$ is equivalent to defining its adjoint morphism
Using Lemma 4.12 and compatibility of pullbacks with tensor products, we need to define a morphism
that is, we need to define a morphism of ![]() $\mathcal {H}_{M_1}\otimes _{\mathfrak {Z}_{M_2}}\mathcal {O}_{[X_{\check P_{12}}^{\rm reg}/\check P_{12}]}$-modules
$\mathcal {H}_{M_1}\otimes _{\mathfrak {Z}_{M_2}}\mathcal {O}_{[X_{\check P_{12}}^{\rm reg}/\check P_{12}]}$-modules
Using the above identifications, we can define this as the composition
 \begin{align} & L\beta_{12}^\ast \mathcal{M}_{M_2}=(L\beta_{12}^\ast\circ R\beta_{12,\ast}\circ R\beta_\ast) (\mathcal{O}_{[X_{\check B_{M_2}}^{\rm reg}/\check B_{M_2}]}) \nonumber\\ &\quad \longrightarrow R\beta_\ast L\alpha^\ast(\mathcal{O}_{[X_{\check B_{M_1}}^{\rm reg}/\check B_{M_1}]}) \xrightarrow{\cong} L\alpha_{12}^\ast R\beta_{M_1,\ast}(\mathcal{O}_{[X_{\check B_{M_1}}^{\rm reg}/\check B_{M_1}]})= L\alpha_{12}^\ast\mathcal{M}_{M_1}, \end{align}
\begin{align} & L\beta_{12}^\ast \mathcal{M}_{M_2}=(L\beta_{12}^\ast\circ R\beta_{12,\ast}\circ R\beta_\ast) (\mathcal{O}_{[X_{\check B_{M_2}}^{\rm reg}/\check B_{M_2}]}) \nonumber\\ &\quad \longrightarrow R\beta_\ast L\alpha^\ast(\mathcal{O}_{[X_{\check B_{M_1}}^{\rm reg}/\check B_{M_1}]}) \xrightarrow{\cong} L\alpha_{12}^\ast R\beta_{M_1,\ast}(\mathcal{O}_{[X_{\check B_{M_1}}^{\rm reg}/\check B_{M_1}]})= L\alpha_{12}^\ast\mathcal{M}_{M_1}, \end{align}where the first morphism is given by adjunction and the second morphism is given by the base change morphism in the cartesian square in (4.13).
A priori this is only a morphism of ![]() $\mathcal {O}_{[X^{\rm reg}_{\check P_{12}}/\check P_{12}]}$-modules.
$\mathcal {O}_{[X^{\rm reg}_{\check P_{12}}/\check P_{12}]}$-modules.
Lemma 4.24 The morphism (4.14) is a morphism of ![]() $\mathcal {H}_{M_1}$-modules.
$\mathcal {H}_{M_1}$-modules.
Proof. We prove the claim after pulling back to ![]() $\tilde X_{\check P_{12}}^{\rm reg}$ in (4.13).
$\tilde X_{\check P_{12}}^{\rm reg}$ in (4.13).
We write ![]() $\tilde \alpha$,
$\tilde \alpha$, ![]() $\tilde \beta$ etc. for the corresponding morphisms of schemes. As all the maps
$\tilde \beta$ etc. for the corresponding morphisms of schemes. As all the maps ![]() $\tilde \beta$ (with various subscripts) are affine, all but the first object in (4.14) are concentrated in degree 0. Moreover, all schemes are reduced, and hence it is enough to prove the claim after restricting to the dense open subscheme where
$\tilde \beta$ (with various subscripts) are affine, all but the first object in (4.14) are concentrated in degree 0. Moreover, all schemes are reduced, and hence it is enough to prove the claim after restricting to the dense open subscheme where ![]() $\varphi$ is regular semi-simple. We denote these open subschemes by
$\varphi$ is regular semi-simple. We denote these open subschemes by ![]() $\tilde X_{\check B_{M_2}}^{\text{reg-ss}}$, etc. Consider the following diagram.
$\tilde X_{\check B_{M_2}}^{\text{reg-ss}}$, etc. Consider the following diagram.

Here, the vertical arrow ![]() $(\ast )$ on the right-hand side is induced by the identification
$(\ast )$ on the right-hand side is induced by the identification
By definition the ![]() $\mathcal {H}_{M_1}$-module structures on source and target of
$\mathcal {H}_{M_1}$-module structures on source and target of
are induced by two (a priori perhaps different) ![]() $\mathcal {H}_{M_1}$-module structures of the structure sheaves
$\mathcal {H}_{M_1}$-module structures of the structure sheaves
which in turn are given by the pullback of an ![]() $\mathcal {H}_{M_1}$-action on
$\mathcal {H}_{M_1}$-action on ![]() $A_{\check T}$. These
$A_{\check T}$. These ![]() $\mathcal {H}_{M_1}$-actions are given by
$\mathcal {H}_{M_1}$-actions are given by
– the
 $\mathcal {H}_{M_1}$ action on
$\mathcal {H}_{M_1}$ action on  $A_{\check T}$ given by
$A_{\check T}$ given by  $A_{\check T}\cong \mathcal {H}_Te_{M_1,{\rm st}}$,
$A_{\check T}\cong \mathcal {H}_Te_{M_1,{\rm st}}$,– the restriction of the
 $\mathcal {H}_{M_2}$ action on
$\mathcal {H}_{M_2}$ action on  $A_{\check T}$ given by
$A_{\check T}$ given by  $A_{\check T}\cong \mathcal {H}_Te_{M_2,{\rm st}}$.
$A_{\check T}\cong \mathcal {H}_Te_{M_2,{\rm st}}$.
By Lemma 4.10(ii) these actions coincide.
We obtain the following first step towards Conjecture 3.2.
Theorem 4.25 For each parabolic ![]() $\mathbb {B}\subset \mathbb {P}\subset \mathbb {G}$ with Levi
$\mathbb {B}\subset \mathbb {P}\subset \mathbb {G}$ with Levi ![]() $\mathbb {M}$ the restriction of (4.11) to the regular locus is a
$\mathbb {M}$ the restriction of (4.11) to the regular locus is a ![]() $\mathfrak {Z}_M$-linear functor
$\mathfrak {Z}_M$-linear functor
Moreover, for two parabolic subgroups ![]() $\mathbb {B}\subset \mathbb {P}_1\subset \mathbb {P}_2$ the natural transformation
$\mathbb {B}\subset \mathbb {P}_1\subset \mathbb {P}_2$ the natural transformation ![]() $\xi _{P_{12}}^{M_2}$ defined in (4.12) is a
$\xi _{P_{12}}^{M_2}$ defined in (4.12) is a ![]() $\mathfrak {Z}_{M_2}$-linear isomorphism.
$\mathfrak {Z}_{M_2}$-linear isomorphism.
For parabolic subgroups ![]() $\mathbb {P}_1\subset \mathbb {P}_2\subset \mathbb {P}_3$ let
$\mathbb {P}_1\subset \mathbb {P}_2\subset \mathbb {P}_3$ let ![]() $\mathbb {M}_3$ denote the Levi quotient of
$\mathbb {M}_3$ denote the Levi quotient of ![]() $\mathbb {P}_3$ and
$\mathbb {P}_3$ and ![]() $\mathbb {P}_{13}\subset \mathbb {P}_{23}$ denote the images of
$\mathbb {P}_{13}\subset \mathbb {P}_{23}$ denote the images of ![]() $\mathbb {P}_1\subset \mathbb {P}_2$ in
$\mathbb {P}_1\subset \mathbb {P}_2$ in ![]() $\mathbb {M}_3$. Then the diagram in Conjecture 3.2(b), applied to
$\mathbb {M}_3$. Then the diagram in Conjecture 3.2(b), applied to ![]() $\mathbb {P}_{13}\subset \mathbb {P}_{23}\subset \mathbb {M}_3$, commutes.
$\mathbb {P}_{13}\subset \mathbb {P}_{23}\subset \mathbb {M}_3$, commutes.
Proof. We are left to prove that ![]() $\xi _{P_{12}}^{M_2}$ is an isomorphism and that the diagram in Conjecture 3.2(b) commutes. Using truncations and resolutions by free modules, it is enough to prove that
$\xi _{P_{12}}^{M_2}$ is an isomorphism and that the diagram in Conjecture 3.2(b) commutes. Using truncations and resolutions by free modules, it is enough to prove that
 \begin{align*} \xi_{P_{12}}^{M_2}(\mathcal{H}_{M_1}):&\ \mathcal{M}_{M_2}={}^t(\mathcal{H}_{M_2}\otimes_{\mathcal{H}_{M_1}} \mathcal{H}_{M_1})\otimes_{\mathcal{H}_{M_2}}\mathcal{M}_{M_2} \\ &\longrightarrow R\beta_{12,\ast}(L\alpha_{12}^\ast \mathcal{M}_{M_1})\cong R\beta_{12,\ast}R\beta_\ast \mathcal{O}_{[X_{\check B_{M_2}}^{\rm reg}/\check B_{M_2}]}=\mathcal{M}_{M_2} \end{align*}
\begin{align*} \xi_{P_{12}}^{M_2}(\mathcal{H}_{M_1}):&\ \mathcal{M}_{M_2}={}^t(\mathcal{H}_{M_2}\otimes_{\mathcal{H}_{M_1}} \mathcal{H}_{M_1})\otimes_{\mathcal{H}_{M_2}}\mathcal{M}_{M_2} \\ &\longrightarrow R\beta_{12,\ast}(L\alpha_{12}^\ast \mathcal{M}_{M_1})\cong R\beta_{12,\ast}R\beta_\ast \mathcal{O}_{[X_{\check B_{M_2}}^{\rm reg}/\check B_{M_2}]}=\mathcal{M}_{M_2} \end{align*}
is an isomorphism. However, this is a direct consequence of the construction of ![]() $\xi _{P_{12}}^{M_2}$ in (4.14) using the base change isomorphism in the cartesian square of (4.13).
$\xi _{P_{12}}^{M_2}$ in (4.14) using the base change isomorphism in the cartesian square of (4.13).
As ![]() $\xi _{P_{12}}^{M_2}$ is the composition of an adjunction morphism and a base change map, the commutativity of (b) in the conjecture is a consequence of standard compatibilities of base change morphisms and adjunctions.
$\xi _{P_{12}}^{M_2}$ is the composition of an adjunction morphism and a base change map, the commutativity of (b) in the conjecture is a consequence of standard compatibilities of base change morphisms and adjunctions.
Remark 4.26 We point out that the arguments above extend directly from the regular locus to all of ![]() $X_{\check G}$ once Conjecture 4.14 is known.
$X_{\check G}$ once Conjecture 4.14 is known.
4.6 Compactly induced representations
We describe the image of the functor ![]() $R_G$ defined in (4.11) on (the
$R_G$ defined in (4.11) on (the ![]() $I$-invariants in) the compactly induced representations
$I$-invariants in) the compactly induced representations ![]() $\operatorname {c-ind}_K^G\sigma _{\mathcal {P}}$. The result parallels, and is motivated by, results of Pyvovarov in [Reference PyvovarovPyv20c].
$\operatorname {c-ind}_K^G\sigma _{\mathcal {P}}$. The result parallels, and is motivated by, results of Pyvovarov in [Reference PyvovarovPyv20c].
Recall from Proposition 2.1(ii) that the irreducible components of ![]() $X_{\check G}$ are in bijection with the possible Jordan canonical forms of the nilpotent endomorphism
$X_{\check G}$ are in bijection with the possible Jordan canonical forms of the nilpotent endomorphism ![]() $N$. For a partition
$N$. For a partition ![]() $\mathcal {P}$ let
$\mathcal {P}$ let ![]() $Z_{\check G,\mathcal {P}}$ denote the irreducible component of
$Z_{\check G,\mathcal {P}}$ denote the irreducible component of ![]() $X_{\check G,\mathcal {P}}$ such that the Jordan canonical form of
$X_{\check G,\mathcal {P}}$ such that the Jordan canonical form of ![]() $N$ at the generic point of
$N$ at the generic point of ![]() $Z_{\check G,\mathcal {P}}$ is given by the partition
$Z_{\check G,\mathcal {P}}$ is given by the partition ![]() $\mathcal {P}$. Then we set
$\mathcal {P}$. Then we set
In particular, we have that ![]() $X_{\check G,\mathcal {P}_{\rm min}}=X_{\check G}$, and
$X_{\check G,\mathcal {P}_{\rm min}}=X_{\check G}$, and ![]() $X_{\check G,\mathcal {P}_{\rm max}}=Z_{\check G,\mathcal {P}_{\rm max}}$ is irreducible. We will sometimes write
$X_{\check G,\mathcal {P}_{\rm max}}=Z_{\check G,\mathcal {P}_{\rm max}}$ is irreducible. We will sometimes write ![]() $X_{\check G,0}$ for this irreducible component, as it is the irreducible component defined by
$X_{\check G,0}$ for this irreducible component, as it is the irreducible component defined by ![]() $N=0$. We write
$N=0$. We write ![]() $\eta _\mathcal {P}$ for the generic point of the irreducible component
$\eta _\mathcal {P}$ for the generic point of the irreducible component ![]() $Z_{\check G,\mathcal {P}}$.
$Z_{\check G,\mathcal {P}}$.
Proposition 4.27 Let ![]() $\mathcal {P}$ be a partition. Then
$\mathcal {P}$ be a partition. Then ![]() $R_G(\operatorname {c-ind}_K^G\sigma _\mathcal {P})$ is concentrated in degree zero and, viewed as a
$R_G(\operatorname {c-ind}_K^G\sigma _\mathcal {P})$ is concentrated in degree zero and, viewed as a ![]() $\check G$-equivariant coherent sheaf on
$\check G$-equivariant coherent sheaf on ![]() $X_{\check G}$, has support
$X_{\check G}$, has support ![]() $X_{\check G,\mathcal {P}}$. Moreover,
$X_{\check G,\mathcal {P}}$. Moreover,
 \begin{align*} R_G((\operatorname{c-ind}_K^G\mathbf{1}_K)^I)&=\mathcal{O}_{X_{\check G,0}},\\ R_G((\operatorname{c-ind}_K^G{\rm st}_G)^I) &=\mathcal{O}_{X_{\check G}}, \end{align*}
\begin{align*} R_G((\operatorname{c-ind}_K^G\mathbf{1}_K)^I)&=\mathcal{O}_{X_{\check G,0}},\\ R_G((\operatorname{c-ind}_K^G{\rm st}_G)^I) &=\mathcal{O}_{X_{\check G}}, \end{align*}
equipped with their canonical ![]() $\check G$-equivariant structures. In particular,
$\check G$-equivariant structures. In particular,
Proof. We will rather calculate the images of
Recall that ![]() $m_{\mathcal {P}_{\rm min}}=m_{\mathcal {P}_{\rm max}}=1$. Using Lemma 4.9, we see that the
$m_{\mathcal {P}_{\rm min}}=m_{\mathcal {P}_{\rm max}}=1$. Using Lemma 4.9, we see that the ![]() $\check G$-equivariant coherent sheaf on
$\check G$-equivariant coherent sheaf on ![]() $X_{\check G}$ defined by
$X_{\check G}$ defined by ![]() $R_G((\operatorname {c-ind}_K^G\Sigma _P)^I)$ is
$R_G((\operatorname {c-ind}_K^G\Sigma _P)^I)$ is ![]() $e_{\mathcal {P}}\mathcal {H}_{G}\otimes _{\mathcal {H}_G}\tilde {\mathcal {M}}_G$.
$e_{\mathcal {P}}\mathcal {H}_{G}\otimes _{\mathcal {H}_G}\tilde {\mathcal {M}}_G$.
Recall that by definition the sheaf ![]() $\tilde {\mathcal {M}}_G$ is the sheaf attached to the image of
$\tilde {\mathcal {M}}_G$ is the sheaf attached to the image of
induced by the surjections ![]() $\mathcal {H}_Ge_{\rm st}\otimes _\mathfrak {Z}k(\eta _{\mathcal {P}'})\rightarrow {\rm LL}(\varphi _{\eta _{\mathcal {P}'}},N_{\eta _{\mathcal {P}'}})^I$ of Lemma 4.7. Consequently,
$\mathcal {H}_Ge_{\rm st}\otimes _\mathfrak {Z}k(\eta _{\mathcal {P}'})\rightarrow {\rm LL}(\varphi _{\eta _{\mathcal {P}'}},N_{\eta _{\mathcal {P}'}})^I$ of Lemma 4.7. Consequently, ![]() $e_{\mathcal {P}}\mathcal {H}_{G}\otimes _{\mathcal {H}_G}\tilde {\mathcal {M}}_G$ is the sheaf defined by the image of the morphism
$e_{\mathcal {P}}\mathcal {H}_{G}\otimes _{\mathcal {H}_G}\tilde {\mathcal {M}}_G$ is the sheaf defined by the image of the morphism
Note that ![]() $A_{\check G}\otimes _{\mathfrak {Z}}e_\mathcal {P}\mathcal {H}_Ge_{\rm st}$ is a free
$A_{\check G}\otimes _{\mathfrak {Z}}e_\mathcal {P}\mathcal {H}_Ge_{\rm st}$ is a free ![]() $A_{\check G}$-module of rank
$A_{\check G}$-module of rank ![]() $m_\mathcal {P}^2$, by Lemma 4.13(iv). To show that the sheaf
$m_\mathcal {P}^2$, by Lemma 4.13(iv). To show that the sheaf ![]() $R_G(\mathcal {H}_Ge_\mathcal {P})$ has support
$R_G(\mathcal {H}_Ge_\mathcal {P})$ has support ![]() $X_{\check G,\mathcal {P}}$ it remains to show that
$X_{\check G,\mathcal {P}}$ it remains to show that
The left-hand side can be identified with
 \begin{align*} {\rm Hom}_{\mathcal{H}_G}(\mathcal{H}_Ge_\mathcal{P},{\rm LL} (\varphi_{\eta_{\mathcal{P}'}},N_{\eta_{\mathcal{P}'}})^I)&= {\rm Hom}_G(\operatorname{c-ind}_K^G\Sigma_\mathcal{P},{\rm LL}(\varphi_{\eta_{\mathcal{P}'}},N_{\eta_{\mathcal{P}'}}))\\ &={\rm Hom}_K(\sigma_{\mathcal{P}},{\rm LL}(\varphi_{\eta_{\mathcal{P}'}},N_{\eta_{\mathcal{P}'}}))^{m_\mathcal{P}}. \end{align*}
\begin{align*} {\rm Hom}_{\mathcal{H}_G}(\mathcal{H}_Ge_\mathcal{P},{\rm LL} (\varphi_{\eta_{\mathcal{P}'}},N_{\eta_{\mathcal{P}'}})^I)&= {\rm Hom}_G(\operatorname{c-ind}_K^G\Sigma_\mathcal{P},{\rm LL}(\varphi_{\eta_{\mathcal{P}'}},N_{\eta_{\mathcal{P}'}}))\\ &={\rm Hom}_K(\sigma_{\mathcal{P}},{\rm LL}(\varphi_{\eta_{\mathcal{P}'}},N_{\eta_{\mathcal{P}'}}))^{m_\mathcal{P}}. \end{align*}
As ![]() ${\rm LL}(\varphi _{\eta _{\mathcal {P}'}},N_{\eta _{\mathcal {P}'}})$ is absolutely irreducible and generic, [Reference ShottonSho18, Theorem 3.7] implies the claim.
${\rm LL}(\varphi _{\eta _{\mathcal {P}'}},N_{\eta _{\mathcal {P}'}})$ is absolutely irreducible and generic, [Reference ShottonSho18, Theorem 3.7] implies the claim.
If ![]() $\mathcal {P}\in \{\mathcal {P}_{\rm min},\mathcal {P}_{\rm max}\}$, then
$\mathcal {P}\in \{\mathcal {P}_{\rm min},\mathcal {P}_{\rm max}\}$, then ![]() $\Sigma _\mathcal {P}=\sigma _\mathcal {P}$ and
$\Sigma _\mathcal {P}=\sigma _\mathcal {P}$ and ![]() $A_{\check G}\otimes _{\mathfrak {Z}}e_\mathcal {P}\mathcal {H}_Ge_{\rm st}\cong A_{\check G}$. In this case the above discussion shows that
$A_{\check G}\otimes _{\mathfrak {Z}}e_\mathcal {P}\mathcal {H}_Ge_{\rm st}\cong A_{\check G}$. In this case the above discussion shows that ![]() $R_G((\operatorname {c-ind}_K^G\sigma _\mathcal {P})^I)$ is the structure sheaf of the union of those irreducible components
$R_G((\operatorname {c-ind}_K^G\sigma _\mathcal {P})^I)$ is the structure sheaf of the union of those irreducible components ![]() $Z_{\check G,\mathcal {P}'}$ such that
$Z_{\check G,\mathcal {P}'}$ such that ![]() ${\rm Hom}_K(\sigma _\mathcal {P},{\rm LL}(\varphi _{\eta _{\mathcal {P}'}},N_{\eta _{\mathcal {P}'}}))\neq 0$. If
${\rm Hom}_K(\sigma _\mathcal {P},{\rm LL}(\varphi _{\eta _{\mathcal {P}'}},N_{\eta _{\mathcal {P}'}}))\neq 0$. If ![]() $\mathcal {P}=\mathcal {P}_{\rm max}$ this implies
$\mathcal {P}=\mathcal {P}_{\rm max}$ this implies ![]() $\mathcal {P}'=\mathcal {P}$ as above. On the other hand, if
$\mathcal {P}'=\mathcal {P}$ as above. On the other hand, if ![]() $\mathcal {P}=\mathcal {P}_{\rm min}$, then
$\mathcal {P}=\mathcal {P}_{\rm min}$, then ![]() ${\rm Hom}_K(\sigma _\mathcal {P},{\rm LL}(\varphi _{\eta _{\mathcal {P}'}},N_{\eta _{\mathcal {P}'}}))\neq 0$ for all
${\rm Hom}_K(\sigma _\mathcal {P},{\rm LL}(\varphi _{\eta _{\mathcal {P}'}},N_{\eta _{\mathcal {P}'}}))\neq 0$ for all ![]() $\mathcal {P}'$ by [Reference PyvovarovPyv20b, Theorem 1.3].
$\mathcal {P}'$ by [Reference PyvovarovPyv20b, Theorem 1.3].
Remark 4.28 A closer analysis of the proof shows that ![]() $R_G(\operatorname {c-ind}_K^G\sigma _\mathcal {P})$ can never be (locally) free over its support
$R_G(\operatorname {c-ind}_K^G\sigma _\mathcal {P})$ can never be (locally) free over its support ![]() $X_{\check G,\mathcal {P}}$ unless
$X_{\check G,\mathcal {P}}$ unless ![]() $m_\mathcal {P}=1$. Indeed, generically on
$m_\mathcal {P}=1$. Indeed, generically on ![]() $Z_{\check G,\mathcal {P}}$ the sheaf
$Z_{\check G,\mathcal {P}}$ the sheaf ![]() $R_G(\operatorname {c-ind}_K^G\sigma _\mathcal {P})$ is free of rank one, using [Reference ShottonSho18, Theorem 3.7 (ii)]. On the other hand, generically on
$R_G(\operatorname {c-ind}_K^G\sigma _\mathcal {P})$ is free of rank one, using [Reference ShottonSho18, Theorem 3.7 (ii)]. On the other hand, generically on ![]() $X_{\check G,0}$ this sheaf is free of rank
$X_{\check G,0}$ this sheaf is free of rank ![]() $m_{\mathcal {P}}$. Indeed, let
$m_{\mathcal {P}}$. Indeed, let ![]() $L$ be the algebraic closure of
$L$ be the algebraic closure of ![]() $k(\eta _{\mathcal {P}_{\rm max}})$. Then
$k(\eta _{\mathcal {P}_{\rm max}})$. Then ![]() ${\rm LL}(\varphi _{\mathcal {P}_{\rm max}},N_{\mathcal {P}_{\rm max}})\otimes _{k(\eta _{\mathcal {P}_{\rm max}})}L$ is an irreducible representation induced from the upper triangular Borel. On the other hand,
${\rm LL}(\varphi _{\mathcal {P}_{\rm max}},N_{\mathcal {P}_{\rm max}})\otimes _{k(\eta _{\mathcal {P}_{\rm max}})}L$ is an irreducible representation induced from the upper triangular Borel. On the other hand, ![]() $\operatorname {c-ind}_K^G\sigma _\mathcal {P}\otimes _{\mathfrak {Z}}K$ is a direct sum of
$\operatorname {c-ind}_K^G\sigma _\mathcal {P}\otimes _{\mathfrak {Z}}K$ is a direct sum of ![]() $m_{\mathcal {P}}$ copies of the same irreducible principal series representation by Corollary 6.1 and Lemma 6.4 of [Reference PyvovarovPyv20a].
$m_{\mathcal {P}}$ copies of the same irreducible principal series representation by Corollary 6.1 and Lemma 6.4 of [Reference PyvovarovPyv20a].
4.7 Remarks about the relation of the various conjectures
In this section we add a few remarks about the relation of Conjecture 4.14 with Conjectures 3.2 and 2.17. This should give some evidence for Conjecture 4.14 which in turn would imply that ![]() $R\tilde \beta _{B,\ast }\mathcal {O}_{\tilde {\mathbf {X}}_{\check B}}$ agrees with the
$R\tilde \beta _{B,\ast }\mathcal {O}_{\tilde {\mathbf {X}}_{\check B}}$ agrees with the ![]() $\mathcal {O}_{X_{\check G}}$-module underlying the Hecke module
$\mathcal {O}_{X_{\check G}}$-module underlying the Hecke module ![]() $\tilde {\mathcal {M}}_G$ defined by the Emerton–Helm family. Moreover, we explain the relation of the main conjecture with Conjecture 4.8.
$\tilde {\mathcal {M}}_G$ defined by the Emerton–Helm family. Moreover, we explain the relation of the main conjecture with Conjecture 4.8.
(a) Before we come to this point, we mention that our expectations about ![]() $R\beta _{B,\ast }\mathcal {O}_{\tilde {\mathbf {X}}_{\check B}}$ imply that, for
$R\beta _{B,\ast }\mathcal {O}_{\tilde {\mathbf {X}}_{\check B}}$ imply that, for ![]() $G={\rm GL}_n$, the functor
$G={\rm GL}_n$, the functor ![]() $R_G$ is uniquely determined by the requirements in Conjecture 3.2. If
$R_G$ is uniquely determined by the requirements in Conjecture 3.2. If ![]() $R_G$ is any functor satisfying the main conjecture, then
$R_G$ is any functor satisfying the main conjecture, then
 \begin{align*} R_G(\operatorname{c-ind}_I^G\mathbf{1}_I)&=R_G(\iota_{\overline B}^G (\operatorname{c-ind}_{T^\circ}\mathbf{1}_{T^\circ}))=R\beta_{B,\ast} (L\alpha_{B}^\ast R_T(\operatorname{c-ind}_{T^\circ}^T \mathbf{1}_{T^\circ}))\\ &=R\beta_{B,\ast}(L\alpha^\ast_B(\mathcal{O}_{[X_{\check T}/\check T]}))=R\beta_{B,\ast} \mathcal{O}_{\tilde{\mathbf{X}}_{\check B}} \end{align*}
\begin{align*} R_G(\operatorname{c-ind}_I^G\mathbf{1}_I)&=R_G(\iota_{\overline B}^G (\operatorname{c-ind}_{T^\circ}\mathbf{1}_{T^\circ}))=R\beta_{B,\ast} (L\alpha_{B}^\ast R_T(\operatorname{c-ind}_{T^\circ}^T \mathbf{1}_{T^\circ}))\\ &=R\beta_{B,\ast}(L\alpha^\ast_B(\mathcal{O}_{[X_{\check T}/\check T]}))=R\beta_{B,\ast} \mathcal{O}_{\tilde{\mathbf{X}}_{\check B}} \end{align*}
which is equipped with a faithful action of ![]() $\mathcal {H}_G={\rm End}_{G}(\operatorname {c-ind}_I^G\mathbf {1}_I)$. Using the identification
$\mathcal {H}_G={\rm End}_{G}(\operatorname {c-ind}_I^G\mathbf {1}_I)$. Using the identification ![]() ${\rm Rep}_{[T,1]}G\cong \mathcal {H}_G\text {-}{\rm mod}$ and resolutions by free
${\rm Rep}_{[T,1]}G\cong \mathcal {H}_G\text {-}{\rm mod}$ and resolutions by free ![]() $\mathcal {H}_G$-modules, we deduce that the functor
$\mathcal {H}_G$-modules, we deduce that the functor ![]() $R_G$ on the category
$R_G$ on the category ![]() $\mathcal {H}_G\text {-}{\rm mod}$ necessarily has to be of the form
$\mathcal {H}_G\text {-}{\rm mod}$ necessarily has to be of the form
As we expect that ![]() $R\beta _{B,\ast }\mathcal {O}_{\tilde {\mathbf {X}}_{\check B}}$ is concentrated in one degree and is a maximal Cohen–Macaulay module the
$R\beta _{B,\ast }\mathcal {O}_{\tilde {\mathbf {X}}_{\check B}}$ is concentrated in one degree and is a maximal Cohen–Macaulay module the ![]() $\mathcal {H}_G$-action (if it exists) is uniquely determined by its specialization at the generic points of
$\mathcal {H}_G$-action (if it exists) is uniquely determined by its specialization at the generic points of ![]() $X_{\check G}$. At these points the Frobenius
$X_{\check G}$. At these points the Frobenius ![]() $\varphi$ is regular semi-simple and we will see in Corollary 4.44 below that in this case the completion of the functor (with respect to the corresponding character of the center
$\varphi$ is regular semi-simple and we will see in Corollary 4.44 below that in this case the completion of the functor (with respect to the corresponding character of the center ![]() $\mathfrak {Z}$) is uniquely determined by the conditions in Conjecture 3.2.
$\mathfrak {Z}$) is uniquely determined by the conditions in Conjecture 3.2.
(b) One could hope that (if Conjecture 2.17 holds true) the Cohen–Macaulay property of ![]() $R\tilde \beta _{B,\ast }\mathcal {O}_{\tilde {\mathbf {X}}_{\check B}}$ implies that the
$R\tilde \beta _{B,\ast }\mathcal {O}_{\tilde {\mathbf {X}}_{\check B}}$ implies that the ![]() $\mathcal {H}_G$-action extends from its restriction to the regular locus to all of
$\mathcal {H}_G$-action extends from its restriction to the regular locus to all of ![]() $X_{\check G}$. Indeed, this would be automatic if the complement of the open dense subset
$X_{\check G}$. Indeed, this would be automatic if the complement of the open dense subset ![]() $X_{\check G}^{\rm reg}$ had codimension greater than or equal to two in
$X_{\check G}^{\rm reg}$ had codimension greater than or equal to two in ![]() $X_{\check G}$. Unfortunately this is not true in general, not even in the case
$X_{\check G}$. Unfortunately this is not true in general, not even in the case ![]() $G={\rm GL}_n$. However, the generic points of
$G={\rm GL}_n$. However, the generic points of ![]() $X_{\check G}\backslash X_{\check G}^{\rm reg}$ that are of codimension one in
$X_{\check G}\backslash X_{\check G}^{\rm reg}$ that are of codimension one in ![]() $X_{\check G}$ can be described rather explicitly. In fact it turns out that they are generic L-parameters and hence
$X_{\check G}$ can be described rather explicitly. In fact it turns out that they are generic L-parameters and hence ![]() $X_{\check G}$ is smooth at these points. It seems likely that Conjecture 4.14 can be checked explicitly (‘by hand’) at these points. This would imply that the
$X_{\check G}$ is smooth at these points. It seems likely that Conjecture 4.14 can be checked explicitly (‘by hand’) at these points. This would imply that the ![]() $\mathcal {H}_G$-action on
$\mathcal {H}_G$-action on ![]() $R\tilde \beta _{B,\ast }\mathcal {O}_{\tilde {\mathbf {X}}_{\check B}}$ is well defined on an open subset
$R\tilde \beta _{B,\ast }\mathcal {O}_{\tilde {\mathbf {X}}_{\check B}}$ is well defined on an open subset ![]() $U$ whose complement has codimension at least
$U$ whose complement has codimension at least ![]() $2$ and hence (using Conjecture 2.17) the Hecke action extends to all of
$2$ and hence (using Conjecture 2.17) the Hecke action extends to all of ![]() $R\tilde \beta _{B,\ast }\mathcal {O}_{\tilde {\mathbf {X}}_{\check B}}$.
$R\tilde \beta _{B,\ast }\mathcal {O}_{\tilde {\mathbf {X}}_{\check B}}$.
(c) We assume Conjectures 2.17 and 3.2 and explain that in this case Conjecture 4.14 can be attacked using the functor ![]() $R_G$. The sheaf
$R_G$. The sheaf
is an ![]() $\mathcal {O}_{X_{\check G}}\otimes _{\mathfrak {Z}}\mathcal {H}_G$-module that is Cohen–Macaulay as an
$\mathcal {O}_{X_{\check G}}\otimes _{\mathfrak {Z}}\mathcal {H}_G$-module that is Cohen–Macaulay as an ![]() $\mathcal {O}_{X_{\check G}}$-module. In particular, its direct summand
$\mathcal {O}_{X_{\check G}}$-module. In particular, its direct summand ![]() $e_{G,{\rm st}}\tilde {\mathcal {M}}'_G$ is a Cohen–Macaulay module as well. If Conjecture 4.14 can be checked on an open subset
$e_{G,{\rm st}}\tilde {\mathcal {M}}'_G$ is a Cohen–Macaulay module as well. If Conjecture 4.14 can be checked on an open subset ![]() $U$ as in (b) above, then
$U$ as in (b) above, then ![]() $e_{G,{\rm st}}\tilde {\mathcal {M}}'_G|_U\cong \mathcal {O}_U$ as in the proof of Proposition 4.27. The Cohen–Macaulay property hence implies that
$e_{G,{\rm st}}\tilde {\mathcal {M}}'_G|_U\cong \mathcal {O}_U$ as in the proof of Proposition 4.27. The Cohen–Macaulay property hence implies that ![]() $e_{G,{\rm st}}\tilde {\mathcal {M}}'_G\cong \mathcal {O}_{X_{\check G}}$ and hence by (4.5) there is a canonical morphism
$e_{G,{\rm st}}\tilde {\mathcal {M}}'_G\cong \mathcal {O}_{X_{\check G}}$ and hence by (4.5) there is a canonical morphism
We expect that this morphism is a surjection, and that this surjection agrees with the surjection in Conjecture 4.14. In fact it seems that this can be checked using properties of the conjectured functor ![]() $R_G(-)={}^t(-)\otimes _{\mathcal {H}_G}^L\tilde {\mathcal {M}}'_G$ (compare (a) above for the fact that
$R_G(-)={}^t(-)\otimes _{\mathcal {H}_G}^L\tilde {\mathcal {M}}'_G$ (compare (a) above for the fact that ![]() $R_G$ necessarily is of this form): We only need to check that for each point
$R_G$ necessarily is of this form): We only need to check that for each point ![]() $x\in X_{\check G}$ the canonical map
$x\in X_{\check G}$ the canonical map
is surjective. As ![]() $e_{G,{\rm st}}\tilde {\mathcal {M}}'_G\otimes k(x)=k(x)$ is one-dimensional there is a unique generic Jordan–Hölder factor
$e_{G,{\rm st}}\tilde {\mathcal {M}}'_G\otimes k(x)=k(x)$ is one-dimensional there is a unique generic Jordan–Hölder factor ![]() $\pi _x$ in
$\pi _x$ in ![]() $\tilde {\mathcal {M}}'_G\otimes k(x)$ and (4.15) is surjective if any only if
$\tilde {\mathcal {M}}'_G\otimes k(x)$ and (4.15) is surjective if any only if ![]() $\pi _x$ is the cosocle of
$\pi _x$ is the cosocle of ![]() $\tilde {\mathcal {M}}'_G\otimes k(x)$. The center
$\tilde {\mathcal {M}}'_G\otimes k(x)$. The center ![]() $\mathfrak {Z}$ acts on
$\mathfrak {Z}$ acts on ![]() $\pi _x$ via a character
$\pi _x$ via a character ![]() $\chi _x:\mathfrak {Z}\rightarrow k(x)$ and there are only finitely many irreducible representations
$\chi _x:\mathfrak {Z}\rightarrow k(x)$ and there are only finitely many irreducible representations ![]() $\pi$ on which
$\pi$ on which ![]() $\mathfrak {Z}$ acts via
$\mathfrak {Z}$ acts via ![]() $\chi _x$. Among those,
$\chi _x$. Among those, ![]() $\pi _x$ is the unique generic one. We expect that for irreducible
$\pi _x$ is the unique generic one. We expect that for irreducible ![]() $\pi$ the complex of coherent sheaves
$\pi$ the complex of coherent sheaves ![]() $R_G(\pi )$ (which is supported in non-positive degrees) has cohomology in degree zero if and only if
$R_G(\pi )$ (which is supported in non-positive degrees) has cohomology in degree zero if and only if ![]() $\pi$ is generic. This implies in particular that
$\pi$ is generic. This implies in particular that ![]() ${}^t\pi \otimes _{\mathcal {H}_G}\tilde {\mathcal {M}}'_G\otimes k(x)=0$ unless
${}^t\pi \otimes _{\mathcal {H}_G}\tilde {\mathcal {M}}'_G\otimes k(x)=0$ unless ![]() $\pi$ is generic. Using the Tensor-Hom adjunction
$\pi$ is generic. Using the Tensor-Hom adjunction
this expectation would imply that the cosocle of ![]() $\tilde {\mathcal {M}}'_G\otimes k(x)$ has to be generic and hence (4.15) must be a surjection.
$\tilde {\mathcal {M}}'_G\otimes k(x)$ has to be generic and hence (4.15) must be a surjection.
(d) We discuss how Conjecture 4.8 relates to Conjecture 3.2 in the cases where ![]() $\varphi$ is not regular semi-simple (i.e. in the cases that are not covered by Corollary 4.20). For
$\varphi$ is not regular semi-simple (i.e. in the cases that are not covered by Corollary 4.20). For ![]() $(\varphi,N)\in X_{\check G}(C)$ let
$(\varphi,N)\in X_{\check G}(C)$ let ![]() $\varphi ^{\rm ss}$ denote the semi-simplification of
$\varphi ^{\rm ss}$ denote the semi-simplification of ![]() $\varphi$. Generalizing Remark 3.3(b), we define a closed
$\varphi$. Generalizing Remark 3.3(b), we define a closed ![]() $\check G$-stable subscheme
$\check G$-stable subscheme ![]() $X_{\check G,[\varphi,N]}\subset X_{\check G}$ as the closed subscheme whose
$X_{\check G,[\varphi,N]}\subset X_{\check G}$ as the closed subscheme whose ![]() $C$-points are the pairs
$C$-points are the pairs ![]() $(\varphi ',N')$ such that
$(\varphi ',N')$ such that ![]() $\varphi '^{\rm ss}\in \check G\cdot \varphi ^{\rm ss}$ and such that
$\varphi '^{\rm ss}\in \check G\cdot \varphi ^{\rm ss}$ and such that ![]() $N'$ lies in the closure of
$N'$ lies in the closure of ![]() $\check G\cdot N$. While it turns out that this closed subscheme still contains
$\check G\cdot N$. While it turns out that this closed subscheme still contains
as an open subscheme, we caution the reader that it is not true in general that ![]() $X^{\circ }_{\check G,[\varphi,N]}$ is dense in
$X^{\circ }_{\check G,[\varphi,N]}$ is dense in ![]() $X_{\check G,[\varphi,N]}$. In fact
$X_{\check G,[\varphi,N]}$. In fact ![]() $X_{\check G,[\varphi,N]}$ can have several irreducible components in general (the lowest-dimensional case where this phenomenon occurs is
$X_{\check G,[\varphi,N]}$ can have several irreducible components in general (the lowest-dimensional case where this phenomenon occurs is ![]() ${\rm GL}_4$ with
${\rm GL}_4$ with ![]() $\varphi ={\rm diag}(1,q,q,q^2)$ and
$\varphi ={\rm diag}(1,q,q,q^2)$ and ![]() $N$ of maximal possible rank).
$N$ of maximal possible rank).
According to the discussion above and assuming Conjecture 4.14, the functor ![]() $R_G$ coincides with the functor
$R_G$ coincides with the functor ![]() $\pi \mapsto {}^t\pi \otimes ^L_{\mathcal {H}_G}\mathcal {M}_G$, and if
$\pi \mapsto {}^t\pi \otimes ^L_{\mathcal {H}_G}\mathcal {M}_G$, and if ![]() $\pi$ is a representation (not just a complex of representations) concentrated in degree zero the complex
$\pi$ is a representation (not just a complex of representations) concentrated in degree zero the complex ![]() $R_G(\pi )$ is concentrated in non-positive degrees. If
$R_G(\pi )$ is concentrated in non-positive degrees. If ![]() $\pi$ is a representation concentrated in degree zero its zeroth cohomology sheaf
$\pi$ is a representation concentrated in degree zero its zeroth cohomology sheaf ![]() $H^0(R_G(\pi ))$ is identified with the non-derived tensor product
$H^0(R_G(\pi ))$ is identified with the non-derived tensor product ![]() ${}^t\pi \otimes _{\mathcal {H}_G}\mathcal {M}_G$ Similarly to (c), we compute that the fiber
${}^t\pi \otimes _{\mathcal {H}_G}\mathcal {M}_G$ Similarly to (c), we compute that the fiber ![]() $H^0(R_G(\pi ))\otimes k(x)$ as the
$H^0(R_G(\pi ))\otimes k(x)$ as the ![]() $k(x)$-dual to
$k(x)$-dual to
Given a point ![]() $x=(\varphi,N)\in X_{\check G}$, we apply this to the modified representations
$x=(\varphi,N)\in X_{\check G}$, we apply this to the modified representations ![]() ${\rm LL}^{\rm mod}(\varphi,N')$ for the various
${\rm LL}^{\rm mod}(\varphi,N')$ for the various ![]() $N'$ such that
$N'$ such that ![]() $(\varphi,N')\in X_{\check G}$. We expect that, generalizing Remark 3.3(b), the sheaf
$(\varphi,N')\in X_{\check G}$. We expect that, generalizing Remark 3.3(b), the sheaf ![]() $H^0(R_G({\rm LL}^{\rm mod}(\varphi,N')))$ has support
$H^0(R_G({\rm LL}^{\rm mod}(\varphi,N')))$ has support ![]() $X_{\check G,[\varphi,N']}$ (we are slightly sloppy about viewing
$X_{\check G,[\varphi,N']}$ (we are slightly sloppy about viewing ![]() $R_G(\pi )$ as a complex of sheaves on
$R_G(\pi )$ as a complex of sheaves on ![]() $[X_{\check G}/\check G]$ or on
$[X_{\check G}/\check G]$ or on ![]() $X_{\check G}$). Hence, we expect that there is a non-trivial morphism
$X_{\check G}$). Hence, we expect that there is a non-trivial morphism
if and only if ![]() $N$ lies in the closure of the
$N$ lies in the closure of the ![]() $\check G$-orbit of
$\check G$-orbit of ![]() $N'$. As the left-hand side and the right-hand side have exactly one generic irreducible constituent which appears as the unique subrepresentation, this morphism (if non-zero) is automatically injective. In particular,
$N'$. As the left-hand side and the right-hand side have exactly one generic irreducible constituent which appears as the unique subrepresentation, this morphism (if non-zero) is automatically injective. In particular, ![]() $(\mathcal {M}_G\otimes k(x))^\vee$ contains
$(\mathcal {M}_G\otimes k(x))^\vee$ contains ![]() ${\rm LL}^{\rm mod}((\varphi,N)^\vee )$. A closer analysis of the representations
${\rm LL}^{\rm mod}((\varphi,N)^\vee )$. A closer analysis of the representations ![]() $(\operatorname {c-ind}_N^G\psi )_{[T,1]}\otimes _\mathfrak {Z}k(x)$, of which
$(\operatorname {c-ind}_N^G\psi )_{[T,1]}\otimes _\mathfrak {Z}k(x)$, of which ![]() $\mathcal {M}_G\otimes k(x)$ is a quotient (again we are sloppy and do not distinguish between a representation and the Hecke module defined by the representation), yields that this inclusion in fact has to be an equality as otherwise there is a non-zero map
$\mathcal {M}_G\otimes k(x)$ is a quotient (again we are sloppy and do not distinguish between a representation and the Hecke module defined by the representation), yields that this inclusion in fact has to be an equality as otherwise there is a non-zero map
for some ![]() $N'$ such that
$N'$ such that ![]() $N$ is not contained in the
$N$ is not contained in the ![]() $\check G$-orbit of
$\check G$-orbit of ![]() $N'$, contradicting our expectations about the support of the sheaf
$N'$, contradicting our expectations about the support of the sheaf ![]() $H^0(R_G({\rm LL}^{\rm mod}(\varphi,N')))$.
$H^0(R_G({\rm LL}^{\rm mod}(\varphi,N')))$.
We note that the discussion above automatically would imply that (4.16) is one-dimensional if non-zero. Hence, it seems reasonable to expect that ![]() $H^0(R_G({\rm LL}^{\rm mod}(\varphi,N)))$ is the structure sheaf of
$H^0(R_G({\rm LL}^{\rm mod}(\varphi,N)))$ is the structure sheaf of ![]() $X_{\check G,[\varphi,N]}$, generalizing the expectations in Remark 3.3(b) (which is Theorem 4.34 below in the case of
$X_{\check G,[\varphi,N]}$, generalizing the expectations in Remark 3.3(b) (which is Theorem 4.34 below in the case of ![]() ${\rm GL}_n$). However, we do not know whether one should expect that
${\rm GL}_n$). However, we do not know whether one should expect that ![]() $R_G({\rm LL}^{\rm mod}(\varphi,N))$ is always concentrated in degree zero.
$R_G({\rm LL}^{\rm mod}(\varphi,N))$ is always concentrated in degree zero.
4.8 Proof of the conjecture for  ${\rm GL}_2$
${\rm GL}_2$
We prove Conjecture 3.2 in the two-dimensional case. In this subsection we use the notation ![]() $G=\operatorname {GL}_2(F)$ and
$G=\operatorname {GL}_2(F)$ and ![]() $\check G$ is the algebraic group
$\check G$ is the algebraic group ![]() $\operatorname {GL}_2$ over
$\operatorname {GL}_2$ over ![]() $C$. In this case the
$C$. In this case the ![]() $\check B$-action on
$\check B$-action on ![]() $\operatorname {Lie} \check B\cap \mathcal {N}_{{\rm GL}_2}$ has two orbits and hence
$\operatorname {Lie} \check B\cap \mathcal {N}_{{\rm GL}_2}$ has two orbits and hence ![]() $X_{\check B}$ is a complete intersection and
$X_{\check B}$ is a complete intersection and ![]() $\mathbf {X}_{\check B}=X_{\check B}$ (see Remark 2.8). Moreover, this remark implies that
$\mathbf {X}_{\check B}=X_{\check B}$ (see Remark 2.8). Moreover, this remark implies that ![]() $X_{\check B}$ is reduced, and both of its irreducible components are the closure of an irreducible component of
$X_{\check B}$ is reduced, and both of its irreducible components are the closure of an irreducible component of ![]() $X_{\check B}^{\rm reg}$. To simplify notation, we will write
$X_{\check B}^{\rm reg}$. To simplify notation, we will write ![]() $X_0=X_{\check G,0}=Z_{\check G,\mathcal {P}_{\rm max}}\subset X_{\check G}$ for the component given by
$X_0=X_{\check G,0}=Z_{\check G,\mathcal {P}_{\rm max}}\subset X_{\check G}$ for the component given by ![]() $N=0$ and
$N=0$ and ![]() $X=X_{\check G}$. Moreover, we sometimes write
$X=X_{\check G}$. Moreover, we sometimes write ![]() $X_1=Z_{\check G,\mathcal {P}_{\rm min}}\subset X$ for the component on which
$X_1=Z_{\check G,\mathcal {P}_{\rm min}}\subset X$ for the component on which ![]() $N$ is generically non-trivial.
$N$ is generically non-trivial.
Proposition 4.29 Conjecture 4.14 is true for ![]() ${\rm GL}_2$. In particular, we obtain an identification
${\rm GL}_2$. In particular, we obtain an identification
Proof. As already discussed above, the claim holds over the open subset ![]() $X_{\check G}^{\rm reg}\subset X=X_{\check G}$. On the other hand, the closed complement of
$X_{\check G}^{\rm reg}\subset X=X_{\check G}$. On the other hand, the closed complement of ![]() $X_{\check G}^{\rm reg}$ has the open neighborhood
$X_{\check G}^{\rm reg}$ has the open neighborhood ![]() $X\backslash X_1$ which is an open subset of
$X\backslash X_1$ which is an open subset of ![]() $\check G$. The claim now follows from the well known fact that
$\check G$. The claim now follows from the well known fact that
has vanishing higher direct images, and its global sections are given by
As a consequence we still can use (4.14) to define a natural transformation
where ![]() $\alpha :[X_{\check B}/\check B]\rightarrow [X_{\check T}/\check T]$ and
$\alpha :[X_{\check B}/\check B]\rightarrow [X_{\check T}/\check T]$ and ![]() $\beta :[X_{\check B}/\check B]\rightarrow [X_{\check G}/\check G]$ are the canonical morphisms. The same computation as in the proof of Theorem 4.25 again shows that this natural transformation is a
$\beta :[X_{\check B}/\check B]\rightarrow [X_{\check G}/\check G]$ are the canonical morphisms. The same computation as in the proof of Theorem 4.25 again shows that this natural transformation is a ![]() $\mathfrak {Z}$-linear isomorphism (compare Remark 4.26).
$\mathfrak {Z}$-linear isomorphism (compare Remark 4.26).
Theorem 4.30 Let ![]() $G={\rm GL}_2(F)$ and
$G={\rm GL}_2(F)$ and ![]() $T\subset B\subset G$ denote the standard maximal torus and the standard Borel, respectively. The functors
$T\subset B\subset G$ denote the standard maximal torus and the standard Borel, respectively. The functors ![]() $R_G$ and
$R_G$ and ![]() $R_T$ defined by (4.11) are fully faithful and the natural transformation
$R_T$ defined by (4.11) are fully faithful and the natural transformation ![]() $\xi _B^G$ defined by (4.17) is a
$\xi _B^G$ defined by (4.17) is a ![]() $\mathfrak {Z}$-linear isomorphism. Moreover,
$\mathfrak {Z}$-linear isomorphism. Moreover,
for a choice of a generic character ![]() $\psi :N\rightarrow C^\times$ of the unipotent radical
$\psi :N\rightarrow C^\times$ of the unipotent radical ![]() $N$ of
$N$ of ![]() $B$.
$B$.
By the above discussion, it remains to show that ![]() $R_G$ is fully faithful. Let us write
$R_G$ is fully faithful. Let us write ![]() $f\in \mathfrak {Z}$ for the element corresponding to the characteristic polynomials of the form
$f\in \mathfrak {Z}$ for the element corresponding to the characteristic polynomials of the form ![]() $(T-\lambda )(T-q\lambda )$ for some indeterminate
$(T-\lambda )(T-q\lambda )$ for some indeterminate ![]() $\lambda$. Then the morphism
$\lambda$. Then the morphism
factors through ![]() $\mathcal {O}_{[X/\check G]}\twoheadrightarrow \mathcal {O}_{[X_0/\check G]}$ and yields a morphism
$\mathcal {O}_{[X/\check G]}\twoheadrightarrow \mathcal {O}_{[X_0/\check G]}$ and yields a morphism
with image ![]() $f\mathcal {O}_{[X/\check G]}$ and cokernel
$f\mathcal {O}_{[X/\check G]}$ and cokernel ![]() $\mathcal {O}_{[X_1/\check G]}$.
$\mathcal {O}_{[X_1/\check G]}$.
Proposition 4.31 Let ![]() $\mathcal {F},\mathcal {G}\in \{\mathcal {O}_{[X/\check G]},\mathcal {O}_{[X_0/\check G]}\}$. Then
$\mathcal {F},\mathcal {G}\in \{\mathcal {O}_{[X/\check G]},\mathcal {O}_{[X_0/\check G]}\}$. Then
 \[ {\rm Ext}^i_{[X/\check G]}(\mathcal{F},\mathcal{G})=\begin{cases}\mathfrak{Z}, & i=0,\\ 0, & i\neq 0.\end{cases} \]
\[ {\rm Ext}^i_{[X/\check G]}(\mathcal{F},\mathcal{G})=\begin{cases}\mathfrak{Z}, & i=0,\\ 0, & i\neq 0.\end{cases} \]
More precisely, a ![]() $\mathfrak {Z}$-basis of
$\mathfrak {Z}$-basis of ![]() ${\rm Hom}={\rm Ext}^0$ is given by the identity if
${\rm Hom}={\rm Ext}^0$ is given by the identity if ![]() $\mathcal {F}=\mathcal {G}$.
$\mathcal {F}=\mathcal {G}$.
If ![]() $\mathcal {F}=\mathcal {O}_{[X/\check G]}$ and
$\mathcal {F}=\mathcal {O}_{[X/\check G]}$ and ![]() $\mathcal {G}=\mathcal {O}_{[X_0/\check G]}$, then a
$\mathcal {G}=\mathcal {O}_{[X_0/\check G]}$, then a ![]() $\mathfrak {Z}$-basis is given by the canonical projection, and if
$\mathfrak {Z}$-basis is given by the canonical projection, and if ![]() $\mathcal {F}=\mathcal {O}_{[X_0/\check G]}$ and
$\mathcal {F}=\mathcal {O}_{[X_0/\check G]}$ and ![]() $\mathcal {G}=\mathcal {O}_{[X/\check G]}$, a
$\mathcal {G}=\mathcal {O}_{[X/\check G]}$, a ![]() $\mathfrak {Z}$-basis is given by the morphism (4.18).
$\mathfrak {Z}$-basis is given by the morphism (4.18).
Proof. We can easily reduce to the case ![]() $C$ algebraically closed.
$C$ algebraically closed.
Consider the canonical projection
We need to compute ![]() $H^i({\rm B}\check G,Rf_\ast R\mathcal {H}om(\mathcal {F},\mathcal {G}))$. As
$H^i({\rm B}\check G,Rf_\ast R\mathcal {H}om(\mathcal {F},\mathcal {G}))$. As ![]() $\check G$ is reductive and the base field
$\check G$ is reductive and the base field ![]() $C$ has characteristic zero, the category of
$C$ has characteristic zero, the category of ![]() $\check G$-representations is semi-simple and hence this vector space is given by
$\check G$-representations is semi-simple and hence this vector space is given by ![]() $H^i(Rf_\ast R\mathcal {H}om(\mathcal {F},\mathcal {G}))^{\check G}$ (compare also [Reference Drinfeld and GaitsgoryDG13, Lemma 2.4.1]). Here we write
$H^i(Rf_\ast R\mathcal {H}om(\mathcal {F},\mathcal {G}))^{\check G}$ (compare also [Reference Drinfeld and GaitsgoryDG13, Lemma 2.4.1]). Here we write ![]() $H^i(Rf_\ast R\mathcal {H}om(\mathcal {F},\mathcal {G}))$ for the
$H^i(Rf_\ast R\mathcal {H}om(\mathcal {F},\mathcal {G}))$ for the ![]() $i$th cohomology sheaf of the complex
$i$th cohomology sheaf of the complex ![]() $Rf_\ast R\mathcal {H}om(\mathcal {F},\mathcal {G})$, which is a sheaf on
$Rf_\ast R\mathcal {H}om(\mathcal {F},\mathcal {G})$, which is a sheaf on ![]() ${\rm B}\check G$, and hence a
${\rm B}\check G$, and hence a ![]() $\check G$-representation.
$\check G$-representation.
Let us write ![]() $\tilde {\mathcal {F}}$ and
$\tilde {\mathcal {F}}$ and ![]() $\tilde {\mathcal {G}}$ for the pullbacks of
$\tilde {\mathcal {G}}$ for the pullbacks of ![]() $\mathcal {F}$ and
$\mathcal {F}$ and ![]() $\mathcal {G}$ to
$\mathcal {G}$ to ![]() $X$. Then, by definition, giving the quasi-coherent sheaf
$X$. Then, by definition, giving the quasi-coherent sheaf ![]() $H^i(Rf_\ast R\mathcal {H}om(\mathcal {F},\mathcal {G}))$ on
$H^i(Rf_\ast R\mathcal {H}om(\mathcal {F},\mathcal {G}))$ on ![]() ${\rm B}\check G$ is the same as giving a
${\rm B}\check G$ is the same as giving a ![]() $\check G$-equivariant structure on
$\check G$-equivariant structure on ![]() $H^i(R\mathcal {H}om(\tilde {\mathcal {F}},\tilde {\mathcal {G}}))$. We conclude that
$H^i(R\mathcal {H}om(\tilde {\mathcal {F}},\tilde {\mathcal {G}}))$. We conclude that
for the canonical ![]() $\check G$-representation on
$\check G$-representation on ![]() ${\rm Ext}^i_X(\tilde {\mathcal {F}},\tilde {\mathcal {G}})$ induced by the
${\rm Ext}^i_X(\tilde {\mathcal {F}},\tilde {\mathcal {G}})$ induced by the ![]() $\check G$-equivariant structures on
$\check G$-equivariant structures on ![]() $\tilde {\mathcal {F}}$ and
$\tilde {\mathcal {F}}$ and ![]() $\tilde {\mathcal {G}}$.
$\tilde {\mathcal {G}}$.
If ![]() $\mathcal {F}=\mathcal {O}_{[X/\check G]}$, then
$\mathcal {F}=\mathcal {O}_{[X/\check G]}$, then
 \[ {\rm Ext}^i_X(\tilde{\mathcal{F}},\tilde{\mathcal{G}})=\begin{cases} \Gamma(X,\tilde{\mathcal{G}}), & i=0,\\ 0, & i\neq 0, \end{cases} \]
\[ {\rm Ext}^i_X(\tilde{\mathcal{F}},\tilde{\mathcal{G}})=\begin{cases} \Gamma(X,\tilde{\mathcal{G}}), & i=0,\\ 0, & i\neq 0, \end{cases} \]
and one easily computes ![]() $\Gamma (X,\tilde {\mathcal {G}})^{\check G}\cong \mathfrak {Z}$ in both cases. Moreover, a
$\Gamma (X,\tilde {\mathcal {G}})^{\check G}\cong \mathfrak {Z}$ in both cases. Moreover, a ![]() $\mathfrak {Z}$-basis is easily identified with the identity or the canonical projection, as claimed.
$\mathfrak {Z}$-basis is easily identified with the identity or the canonical projection, as claimed.
Now assume that ![]() $\mathcal {F}=\mathcal {O}_{[X_0/\check G]}$. We compute
$\mathcal {F}=\mathcal {O}_{[X_0/\check G]}$. We compute
If ![]() $i\neq 0$, the sheaf
$i\neq 0$, the sheaf ![]() $\mathcal {E}xt^i_{\mathcal {O}_X}(\tilde {\mathcal {F}},\tilde {\mathcal {G}})$ clearly is supported on the intersection
$\mathcal {E}xt^i_{\mathcal {O}_X}(\tilde {\mathcal {F}},\tilde {\mathcal {G}})$ clearly is supported on the intersection ![]() $X_0\cap X_1$. We first show that it is a locally free sheaf on
$X_0\cap X_1$. We first show that it is a locally free sheaf on ![]() $X_0\cap X_1$ (equipped with the reduced scheme structure). Let
$X_0\cap X_1$ (equipped with the reduced scheme structure). Let ![]() $X^{\text {reg-ss}}\subset X$ denote the Zariski open subset of
$X^{\text {reg-ss}}\subset X$ denote the Zariski open subset of ![]() $(\varphi,N)$ with
$(\varphi,N)$ with ![]() $\varphi$ regular semi-simple. Then
$\varphi$ regular semi-simple. Then ![]() $X_0\cap X_1\subset X^{\text {reg-ss}}$.
$X_0\cap X_1\subset X^{\text {reg-ss}}$.
Moreover, let ![]() $X'\rightarrow X^{\text {reg-ss}}$ denote the scheme parametrizing a
$X'\rightarrow X^{\text {reg-ss}}$ denote the scheme parametrizing a ![]() $\varphi$-stable subspace. This is an étale Galois cover of degree two and the filtration by the universal
$\varphi$-stable subspace. This is an étale Galois cover of degree two and the filtration by the universal ![]() $\varphi$-stable subspace has a canonical
$\varphi$-stable subspace has a canonical ![]() $\varphi$-stable splitting. Let us write
$\varphi$-stable splitting. Let us write ![]() $V_1$ and
$V_1$ and ![]() $V_2$ for these eigenspaces and let
$V_2$ for these eigenspaces and let ![]() $Y\rightarrow \tilde X'$ denote the
$Y\rightarrow \tilde X'$ denote the ![]() $\check T$-torsor trivializing
$\check T$-torsor trivializing ![]() $V_1$ and
$V_1$ and ![]() $V_2$. Moreover, let
$V_2$. Moreover, let
equipped with the ![]() $\check T=\operatorname {Spec} C[s_1^{\pm 1},s_2^{\pm 1}]$-action that is trivial on
$\check T=\operatorname {Spec} C[s_1^{\pm 1},s_2^{\pm 1}]$-action that is trivial on ![]() $\check T$ and via multiplication with the character
$\check T$ and via multiplication with the character ![]() $\alpha :(s_1,s_2)\mapsto s_1s_2^{-1}$ on
$\alpha :(s_1,s_2)\mapsto s_1s_2^{-1}$ on ![]() $a$, and via
$a$, and via ![]() $\alpha ^{-1}$ on
$\alpha ^{-1}$ on ![]() $b$. We consider the diagram
$b$. We consider the diagram

where ![]() $\beta$ is the canonical projection, which is
$\beta$ is the canonical projection, which is ![]() $\check G$-equivariant, and
$\check G$-equivariant, and ![]() $\gamma$ is the
$\gamma$ is the ![]() $\check T$-equivariant
$\check T$-equivariant ![]() $\check G$-torsor that is given by writing the matrices of
$\check G$-torsor that is given by writing the matrices of ![]() $\varphi$ and
$\varphi$ and ![]() $N$ over
$N$ over ![]() $Y$ as
$Y$ as
in the chosen basis of ![]() $V_1$ and
$V_1$ and ![]() $V_2$.
$V_2$.
Let ![]() $x=(\varphi _0,0)\in X_0\cap X_1$ be a
$x=(\varphi _0,0)\in X_0\cap X_1$ be a ![]() $C$-valued point. Without loss of generality we may assume
$C$-valued point. Without loss of generality we may assume ![]() $\varphi _0={\rm diag}(\lambda _0,q\lambda _0)$. Let
$\varphi _0={\rm diag}(\lambda _0,q\lambda _0)$. Let ![]() $y\in Y$ be a pre-image of
$y\in Y$ be a pre-image of ![]() $x$ and let
$x$ and let ![]() $z$ denote its image in
$z$ denote its image in ![]() $Z$, such that
$Z$, such that ![]() $z=(\lambda _0,q\lambda _0,0,0)$. Consider the closed subscheme
$z=(\lambda _0,q\lambda _0,0,0)$. Consider the closed subscheme ![]() $Z_0=V(a,b)\subset Z$ and write
$Z_0=V(a,b)\subset Z$ and write ![]() $\mathcal {F}_Z=\mathcal {O}_{Z_0}$ and
$\mathcal {F}_Z=\mathcal {O}_{Z_0}$ and
 \[ \mathcal{G}_Z=\begin{cases} \mathcal{O}_Z, & \text{if}\ \tilde{\mathcal{G}}=\mathcal{O}_X,\\ \mathcal{O}_{Z_0}, & \text{if}\ \tilde{\mathcal{G}}=\mathcal{O}_{X_0}. \end{cases} \]
\[ \mathcal{G}_Z=\begin{cases} \mathcal{O}_Z, & \text{if}\ \tilde{\mathcal{G}}=\mathcal{O}_X,\\ \mathcal{O}_{Z_0}, & \text{if}\ \tilde{\mathcal{G}}=\mathcal{O}_{X_0}. \end{cases} \]
Then ![]() $\mathcal {E}xt^i_{\mathcal {O}_X}(\tilde {\mathcal {F}},\tilde {\mathcal {G}})$ is locally free on
$\mathcal {E}xt^i_{\mathcal {O}_X}(\tilde {\mathcal {F}},\tilde {\mathcal {G}})$ is locally free on ![]() $X_0\cap X_1$ if and only if
$X_0\cap X_1$ if and only if ![]() $\mathcal {E}xt^i_{\mathcal {O}_Z}(\mathcal {F}_Z,\mathcal {G}_Z)$ is locally free on
$\mathcal {E}xt^i_{\mathcal {O}_Z}(\mathcal {F}_Z,\mathcal {G}_Z)$ is locally free on ![]() $Z_0$. Let
$Z_0$. Let ![]() $S=\hat {\mathcal {O}}_{Z,z}\cong C[\![t_1,t_2,a]\!]/((t_1-t_2)a)$ be the complete local ring at
$S=\hat {\mathcal {O}}_{Z,z}\cong C[\![t_1,t_2,a]\!]/((t_1-t_2)a)$ be the complete local ring at ![]() $z$ with
$z$ with ![]() $\lambda _1=\lambda _0+t_1$ and
$\lambda _1=\lambda _0+t_1$ and ![]() $\lambda _2=q(\lambda _0+t_2)$, and consider the
$\lambda _2=q(\lambda _0+t_2)$, and consider the ![]() $\check T$-equivariant resolution of
$\check T$-equivariant resolution of ![]() $\hat {\mathcal {F}}_{Z,z}=S/(a)$ given by
$\hat {\mathcal {F}}_{Z,z}=S/(a)$ given by
Here ![]() $S(m)$ is the free
$S(m)$ is the free ![]() $S$-module of rank one with the
$S$-module of rank one with the ![]() $\check T$-action twisted by the multiplication with
$\check T$-action twisted by the multiplication with ![]() $\alpha ^m$. It follows that
$\alpha ^m$. It follows that
 \[ {\rm Ext}^i_S(S/(a),S)=\begin{cases} S/(a), & i=0,\\ 0, & i\geq 1, \end{cases} \]
\[ {\rm Ext}^i_S(S/(a),S)=\begin{cases} S/(a), & i=0,\\ 0, & i\geq 1, \end{cases} \]
and
 \[ {\rm Ext}^i_A(S/(a),S/(a))=\begin{cases} S/(a), & i=0,\\ 0, & i\ \text{odd}, \\ (S/(t_1-t_2,a))(-i/2), & i\geq 2\ \text{even}. \end{cases} \]
\[ {\rm Ext}^i_A(S/(a),S/(a))=\begin{cases} S/(a), & i=0,\\ 0, & i\ \text{odd}, \\ (S/(t_1-t_2,a))(-i/2), & i\geq 2\ \text{even}. \end{cases} \]
In particular, ![]() $\mathcal {E}xt^i_{\mathcal {O}_Z}(\mathcal {F}_Z,\mathcal {O}_Z)$ vanishes for
$\mathcal {E}xt^i_{\mathcal {O}_Z}(\mathcal {F}_Z,\mathcal {O}_Z)$ vanishes for ![]() $i\neq 0$, and
$i\neq 0$, and ![]() $\mathcal {E}xt^i_{\mathcal {O}_Z}(\mathcal {F}_Z,\mathcal {O}_{Z_0})$ vanishes for odd
$\mathcal {E}xt^i_{\mathcal {O}_Z}(\mathcal {F}_Z,\mathcal {O}_{Z_0})$ vanishes for odd ![]() $i$ and is locally free of rank one over
$i$ and is locally free of rank one over ![]() $Z_0$ for non-zero even
$Z_0$ for non-zero even ![]() $i$. We deduce
$i$. We deduce
Moreover, it follows that ![]() $\mathcal {E}xt^i_{\mathcal {O}_X}(\tilde {\mathcal {F}},\mathcal {O}_{X_0})$ vanishes for odd
$\mathcal {E}xt^i_{\mathcal {O}_X}(\tilde {\mathcal {F}},\mathcal {O}_{X_0})$ vanishes for odd ![]() $i$ and is locally free of rank one on
$i$ and is locally free of rank one on ![]() $X_0\cap X_1$ for non-zero even
$X_0\cap X_1$ for non-zero even ![]() $i$. In particular, a
$i$. In particular, a ![]() $\check G$-invariant global section
$\check G$-invariant global section
vanishes if
for all ![]() $x'\in X_0\cap X_1$. Hence, we have to show
$x'\in X_0\cap X_1$. Hence, we have to show ![]() $h(x')=0$ for all
$h(x')=0$ for all ![]() $x'\in X_0\cap X_1$ for even
$x'\in X_0\cap X_1$ for even ![]() $i\neq 0$. Again it is enough to check this for our choice
$i\neq 0$. Again it is enough to check this for our choice ![]() $x=(\varphi _0,0)$. Then
$x=(\varphi _0,0)$. Then ![]() $\check T={\rm Stab}_{\operatorname {GL}_2}(\varphi _0)$ acts on the fiber
$\check T={\rm Stab}_{\operatorname {GL}_2}(\varphi _0)$ acts on the fiber ![]() $\mathcal {E}xt^i_{\mathcal {O}_X}(\tilde {\mathcal {F}},\mathcal {O}_{X_0})\otimes k(x)$, and
$\mathcal {E}xt^i_{\mathcal {O}_X}(\tilde {\mathcal {F}},\mathcal {O}_{X_0})\otimes k(x)$, and ![]() $h(x)$ is
$h(x)$ is ![]() $\check T$-invariant. By the above diagram the
$\check T$-invariant. By the above diagram the ![]() $\check T$-action on this fiber is the same as the
$\check T$-action on this fiber is the same as the ![]() $\check T$-action on
$\check T$-action on
 \[ \mathcal{E}xt^i_{\mathcal{O}_Z}(\mathcal{F}_Z,\mathcal{O}_{Z_0})\otimes k(z)=\begin{cases} 0, & i\ \text{odd},\\ C(-i/2), & i\geq 2\ \text{even}. \end{cases} \]
\[ \mathcal{E}xt^i_{\mathcal{O}_Z}(\mathcal{F}_Z,\mathcal{O}_{Z_0})\otimes k(z)=\begin{cases} 0, & i\ \text{odd},\\ C(-i/2), & i\geq 2\ \text{even}. \end{cases} \]
Obviously, for ![]() $i\neq 0$, there are no non-trivial
$i\neq 0$, there are no non-trivial ![]() $\check T$-invariants.
$\check T$-invariants.
It remains to show that ![]() ${\rm Hom}_{[X/\check G]}(\mathcal {O}_{[X_0/\check G]},{\mathcal {G}})\cong \mathfrak {Z}$, and to identify the basis vector. If
${\rm Hom}_{[X/\check G]}(\mathcal {O}_{[X_0/\check G]},{\mathcal {G}})\cong \mathfrak {Z}$, and to identify the basis vector. If ![]() $\mathcal {G}=\mathcal {O}_{[X_0/\check G]}$ this is clear, and a
$\mathcal {G}=\mathcal {O}_{[X_0/\check G]}$ this is clear, and a ![]() $\mathfrak {Z}$-basis is clearly given by the identity. If
$\mathfrak {Z}$-basis is clearly given by the identity. If ![]() $\mathcal {G}=\mathcal {O}_{[X/\check G]}$, one computes that the pullback of the morphism (4.18) to
$\mathcal {G}=\mathcal {O}_{[X/\check G]}$, one computes that the pullback of the morphism (4.18) to ![]() $Y$ specializes to the pullback of a basis vector of
$Y$ specializes to the pullback of a basis vector of ![]() $\mathcal {H}om_{\mathcal {O}_{Z}}(\mathcal {O}_{Z_0},\mathcal {O}_Z)\otimes k(\gamma (y))$ at every point of
$\mathcal {H}om_{\mathcal {O}_{Z}}(\mathcal {O}_{Z_0},\mathcal {O}_Z)\otimes k(\gamma (y))$ at every point of ![]() $y\in Y$. The claim easily follows from this.
$y\in Y$. The claim easily follows from this.
Corollary 4.32 Let ![]() $D_1,D_2\in \{\mathcal {H}_G e_K,\mathcal {H}_G e_{\rm st}\}$. The functor
$D_1,D_2\in \{\mathcal {H}_G e_K,\mathcal {H}_G e_{\rm st}\}$. The functor ![]() $R_G$ induces isomorphisms
$R_G$ induces isomorphisms
Proof. Note that ![]() $\mathcal {H}_G e_K$ and
$\mathcal {H}_G e_K$ and ![]() $\mathcal {H}_G e_{\rm st}$ are projective and
$\mathcal {H}_G e_{\rm st}$ are projective and ![]() ${\rm Hom}_{\mathcal {H}_G}(D_1,D_2)\cong \mathfrak {Z}$. By Proposition 4.31 the claim is true for
${\rm Hom}_{\mathcal {H}_G}(D_1,D_2)\cong \mathfrak {Z}$. By Proposition 4.31 the claim is true for ![]() $i\neq 0$ and we are left to show that in degree zero the canonical morphism identifies basis vectors. This is clear if
$i\neq 0$ and we are left to show that in degree zero the canonical morphism identifies basis vectors. This is clear if ![]() $D_1=D_2$. Let us write
$D_1=D_2$. Let us write ![]() $\gamma _1:\mathcal {H}_G e_K\rightarrow \mathcal {H}_G e_{\rm st}$ and
$\gamma _1:\mathcal {H}_G e_K\rightarrow \mathcal {H}_G e_{\rm st}$ and ![]() $\gamma _2:\mathcal {H}_G e_{\rm st}\rightarrow \mathcal {H}_G e_K$ for choices of basis vectors and let
$\gamma _2:\mathcal {H}_G e_{\rm st}\rightarrow \mathcal {H}_G e_K$ for choices of basis vectors and let ![]() $f\in \mathfrak {Z}$ as defined before Proposition 4.31. Then, up to scalars in
$f\in \mathfrak {Z}$ as defined before Proposition 4.31. Then, up to scalars in ![]() $\mathfrak {Z}^\times$, we have
$\mathfrak {Z}^\times$, we have
Writing ![]() $\delta _i=R_G(\gamma _i)$ one checks that the equalities
$\delta _i=R_G(\gamma _i)$ one checks that the equalities
enforce that
are basis vectors.
Proof of Theorem 4.30 We show that
is fully faithful. The general case then follows from a limit argument as in Remark 3.3(a).
By standard arguments the proof boils down to Corollary 4.32. Let ![]() $D_1^\bullet, D_2^\bullet$ be complexes in
$D_1^\bullet, D_2^\bullet$ be complexes in ![]() ${\bf D}^b(\mathcal {H}_G\text {-mod}_{\text {fg}})$. We may choose representatives of
${\bf D}^b(\mathcal {H}_G\text {-mod}_{\text {fg}})$. We may choose representatives of ![]() $D_i^\bullet$ consisting of bounded complexes whose entries are direct sums of copies of
$D_i^\bullet$ consisting of bounded complexes whose entries are direct sums of copies of ![]() $\mathcal {H}_G e_K$ and
$\mathcal {H}_G e_K$ and ![]() $\mathcal {H}_G e_{\rm st}$. Assume first
$\mathcal {H}_G e_{\rm st}$. Assume first ![]() $D_1^\bullet =\mathcal {H}_G e_K$ or
$D_1^\bullet =\mathcal {H}_G e_K$ or ![]() $\mathcal {H}_G e_{\rm st}$ concentrated in degree zero. We prove the claim by induction on the length of
$\mathcal {H}_G e_{\rm st}$ concentrated in degree zero. We prove the claim by induction on the length of ![]() $D_2^\bullet$. By Corollary 4.32 the claim is true if
$D_2^\bullet$. By Corollary 4.32 the claim is true if ![]() $D_2^\bullet$ has length zero, that is, if
$D_2^\bullet$ has length zero, that is, if ![]() $D_2^\bullet$ is concentrated in a single degree. Assume the claim is true for all complexes of length less than or equal to
$D_2^\bullet$ is concentrated in a single degree. Assume the claim is true for all complexes of length less than or equal to ![]() $m$ and let
$m$ and let ![]() $D_2^\bullet$ be a complex in degrees
$D_2^\bullet$ be a complex in degrees ![]() $[r,r+m+1]$ for some
$[r,r+m+1]$ for some ![]() $r\in \mathbb {Z}$. Then
$r\in \mathbb {Z}$. Then ![]() $D_2^\bullet$ can be identified with the mapping cone of a morphism of complexes
$D_2^\bullet$ can be identified with the mapping cone of a morphism of complexes
with ![]() $\tilde {D}_2^\bullet$ concentrated in degree
$\tilde {D}_2^\bullet$ concentrated in degree ![]() $[r,r+m]$. The claim follows from the induction hypothesis, Corollary 4.32 and the long exact cohomology sequence.
$[r,r+m]$. The claim follows from the induction hypothesis, Corollary 4.32 and the long exact cohomology sequence.
The general case follows by a similar induction on the length of ![]() $D_1^\bullet$.
$D_1^\bullet$.
Example 4.33 We finish this section with some remarks about the case ![]() $G={\rm SL}_2(F)$ and
$G={\rm SL}_2(F)$ and ![]() $\check G={\rm PGL}_2$. As already pointed out above, Conjecture 4.14 fails for
$\check G={\rm PGL}_2$. As already pointed out above, Conjecture 4.14 fails for ![]() ${\rm SL}_2$.
${\rm SL}_2$.
In this case ![]() $\check T=\mathbb {G}_m$ and
$\check T=\mathbb {G}_m$ and ![]() $W=\mathcal {S}_2$. Let us write
$W=\mathcal {S}_2$. Let us write
for the Grothendieck resolution of ![]() ${\rm PGL}_2$, that is for the closed subscheme of
${\rm PGL}_2$, that is for the closed subscheme of ![]() $(g,L)\in {\rm PGL}_2\times \mathbb {P}^1$ such that the line
$(g,L)\in {\rm PGL}_2\times \mathbb {P}^1$ such that the line ![]() $L$ is stable under
$L$ is stable under ![]() $g$. We consider the following canonical diagram.
$g$. We consider the following canonical diagram.

Again it is well known that ![]() $Rf_\ast \mathcal {O}_{\widetilde {\rm PGL}_2}$ is concentrated in degree zero and in fact locally free (necessarily of rank two). However, the canonical map
$Rf_\ast \mathcal {O}_{\widetilde {\rm PGL}_2}$ is concentrated in degree zero and in fact locally free (necessarily of rank two). However, the canonical map
where ![]() $C[T]=\Gamma (\mathbb {G}_m/\mathcal {S}_2, \mathcal {O}_{\mathbb {G}_m/\mathcal {S}_2})$ and
$C[T]=\Gamma (\mathbb {G}_m/\mathcal {S}_2, \mathcal {O}_{\mathbb {G}_m/\mathcal {S}_2})$ and ![]() $C[X,X^{-1}]=\Gamma (\mathbb {G}_m,\mathcal {O}_{\mathbb {G}_m})$, is not surjective. Indeed, consider the point
$C[X,X^{-1}]=\Gamma (\mathbb {G}_m,\mathcal {O}_{\mathbb {G}_m})$, is not surjective. Indeed, consider the point ![]() $x\in {\rm PGL}_2$ given by the class of the diagonal matrix
$x\in {\rm PGL}_2$ given by the class of the diagonal matrix ![]() ${\rm diag}(-1,1)$. Then
${\rm diag}(-1,1)$. Then ![]() $f^{-1}(x)=\{0,\infty \}$ is the disjoint union of two points and hence
$f^{-1}(x)=\{0,\infty \}$ is the disjoint union of two points and hence
as a ![]() $k(x)$-algebra. On the other hand, the morphism
$k(x)$-algebra. On the other hand, the morphism ![]() $C[T]\rightarrow C[X,X^{-1}]$ is given by
$C[T]\rightarrow C[X,X^{-1}]$ is given by ![]() $T\mapsto X+X^{-1}$ and
$T\mapsto X+X^{-1}$ and ![]() $x$ maps to the point
$x$ maps to the point ![]() $\{T=-2\}$ in
$\{T=-2\}$ in ![]() $\operatorname {Spec} C[T]=\mathbb {G}_m/\mathcal {S}_2$. We find that the canonical map (4.20) specializes to
$\operatorname {Spec} C[T]=\mathbb {G}_m/\mathcal {S}_2$. We find that the canonical map (4.20) specializes to
which cannot be surjective. In fact ![]() ${\rm Pic}({\rm PGL}_2)={\rm Hom}(\pi _1({\rm PGL_2}),\mathbb {G}_m)=\mathbb {Z}/2\mathbb {Z}$ and hence there is (up to isomorphism) a unique non-trivial line bundle
${\rm Pic}({\rm PGL}_2)={\rm Hom}(\pi _1({\rm PGL_2}),\mathbb {G}_m)=\mathbb {Z}/2\mathbb {Z}$ and hence there is (up to isomorphism) a unique non-trivial line bundle ![]() $\mathcal {L}$ (which comes with a canonical
$\mathcal {L}$ (which comes with a canonical ![]() ${\rm PGL}_2$-equivariant structure). In fact
${\rm PGL}_2$-equivariant structure). In fact ![]() $\mathcal {L}$ can be identified with the ideal sheaf of the closed subscheme
$\mathcal {L}$ can be identified with the ideal sheaf of the closed subscheme ![]() $\check G\cdot x$ and
$\check G\cdot x$ and ![]() $\mathcal {L}^\vee \cong \mathcal {L}$. It is not hard to show that
$\mathcal {L}^\vee \cong \mathcal {L}$. It is not hard to show that
Let us also mention what ![]() $R\tilde \beta _{B,\ast }\mathcal {O}_{{X}_{\check B}}$ looks like. As in the case of
$R\tilde \beta _{B,\ast }\mathcal {O}_{{X}_{\check B}}$ looks like. As in the case of ![]() ${\rm GL}_2$, the scheme
${\rm GL}_2$, the scheme ![]() $X_{\check G}$ has two irreducible components
$X_{\check G}$ has two irreducible components ![]() $X_{\check G,0}$ and
$X_{\check G,0}$ and ![]() $X_{\check G,1}$, where
$X_{\check G,1}$, where ![]() $N=0$ on
$N=0$ on ![]() $X_{\check G,0}$. Using (4.21), we obtain a decomposition
$X_{\check G,0}$. Using (4.21), we obtain a decomposition
where ![]() $\mathcal {F}$ (respectively,
$\mathcal {F}$ (respectively, ![]() $\mathcal {F}_0$) is the twist of
$\mathcal {F}_0$) is the twist of ![]() $\mathcal {O}_{X_{\check G}}$ (respectively,
$\mathcal {O}_{X_{\check G}}$ (respectively, ![]() $\mathcal {O}_{X_{\check G,0}}$) by the pullback of the non-trivial line bundle
$\mathcal {O}_{X_{\check G,0}}$) by the pullback of the non-trivial line bundle ![]() $\mathcal {L}$ on
$\mathcal {L}$ on ![]() $\check G={\rm PGL}_2$. Indeed, the same computation as for
$\check G={\rm PGL}_2$. Indeed, the same computation as for ![]() ${\rm GL}_2$ yields that
${\rm GL}_2$ yields that
and we can use (4.21) and the canonical morphism ![]() $\mathcal {O}_{X_{\check G}}\rightarrow R\tilde \beta _{B,\ast }\mathcal {O}_{\tilde X_{\check B}}$ to obtain a short exact sequence
$\mathcal {O}_{X_{\check G}}\rightarrow R\tilde \beta _{B,\ast }\mathcal {O}_{\tilde X_{\check B}}$ to obtain a short exact sequence
which has to split using the computation of Ext-groups. Note that the pullback of ![]() $\mathcal {L}$ to
$\mathcal {L}$ to ![]() $\widetilde {\rm PGL}_2$ is the trivial line bundle, and hence twisting this sequence by the line bundle
$\widetilde {\rm PGL}_2$ is the trivial line bundle, and hence twisting this sequence by the line bundle ![]() $\mathcal {F}$ and using the projection formula, we obtain a short exact sequence
$\mathcal {F}$ and using the projection formula, we obtain a short exact sequence
which has to split as well.
We point out that in light of the main conjecture the decompositions (4.22) correspond to the two decompositions
of representation of ![]() $G={\rm SL}_2(F)$, where
$G={\rm SL}_2(F)$, where ![]() $I$ is a choice of an Iwahori and
$I$ is a choice of an Iwahori and ![]() $K_1$ and
$K_1$ and ![]() $K_2$ are the two non-conjugate hyperspecial subgroups of
$K_2$ are the two non-conjugate hyperspecial subgroups of ![]() $G$ with
$G$ with ![]() $I=K_1\cap K_2$. Moreover,
$I=K_1\cap K_2$. Moreover, ![]() $K_1\cong K_2\cong {\rm SL}_2(\mathcal {O}_F)$ and
$K_1\cong K_2\cong {\rm SL}_2(\mathcal {O}_F)$ and ![]() ${\rm st}_{K_i}$ is the respective inflation of the finite-dimensional Steinberg representation of
${\rm st}_{K_i}$ is the respective inflation of the finite-dimensional Steinberg representation of ![]() ${\rm SL}_2(k_F)$.
${\rm SL}_2(k_F)$.
Let us finally comment on the comparison with the Emerton–Helm construction (for a choice of a Whittaker datum ![]() $\psi$). Indeed, choosing
$\psi$). Indeed, choosing ![]() $\psi$, we can again compute that
$\psi$, we can again compute that ![]() $\mathcal {H}_G e_{\psi }=(\operatorname {c-ind}_N^G\psi )^I$ for some idempotent element
$\mathcal {H}_G e_{\psi }=(\operatorname {c-ind}_N^G\psi )^I$ for some idempotent element ![]() $e_\psi$ and this module is free of rank one over
$e_\psi$ and this module is free of rank one over ![]() $\mathcal {H}_T$. We can define an ‘Emerton–Helm family’
$\mathcal {H}_T$. We can define an ‘Emerton–Helm family’ ![]() $\mathcal {V}_{G,\psi }$ as the quotient
$\mathcal {V}_{G,\psi }$ as the quotient
with prescribed fibers at the generic points of ![]() $X_{\check G}$. The fiber of
$X_{\check G}$. The fiber of ![]() $\mathcal {V}_{G,\psi }$ at the point
$\mathcal {V}_{G,\psi }$ at the point ![]() $(x,0)\in X_{\check G}$, for
$(x,0)\in X_{\check G}$, for ![]() $x\in {\rm PGL}_2$ as above, is the representation
$x\in {\rm PGL}_2$ as above, is the representation ![]() $\operatorname {c-ind}_N^G\psi \otimes _{\mathfrak {Z}}k(x)$ which is the unique non-split extension
$\operatorname {c-ind}_N^G\psi \otimes _{\mathfrak {Z}}k(x)$ which is the unique non-split extension
where ![]() $\pi _{x}^{\psi \text {-}{\rm gen}}$ is the
$\pi _{x}^{\psi \text {-}{\rm gen}}$ is the ![]() $\psi$-generic representation on the L-packet defined by
$\psi$-generic representation on the L-packet defined by ![]() $(x,0)$ and
$(x,0)$ and ![]() $\psi '$ is (a choice of) the Whittaker datum not conjugate to
$\psi '$ is (a choice of) the Whittaker datum not conjugate to ![]() $\psi$.
$\psi$.
On the other hand, we obtain a diagram

of ![]() $\mathcal {O}_{X_{\check G}}$-modules. The morphism
$\mathcal {O}_{X_{\check G}}$-modules. The morphism ![]() $g$ is an injection and induces an isomorphism on the open complement
$g$ is an injection and induces an isomorphism on the open complement ![]() $U$ of the Cartier divisor
$U$ of the Cartier divisor ![]() $\check G\cdot (x,0)\subset X_{\check G}$, and
$\check G\cdot (x,0)\subset X_{\check G}$, and
is stable under the action of ![]() $\mathcal {H}_G$, where
$\mathcal {H}_G$, where ![]() $j_U:U\hookrightarrow X_{\check G}$ is the canonical embedding.
$j_U:U\hookrightarrow X_{\check G}$ is the canonical embedding.
This construction equips ![]() $\tilde \beta _{B,\ast }\mathcal {O}_{\tilde {X}_{\check B}} =R\tilde \beta _{B,\ast }\mathcal {O}_{\tilde {X}_{\check B}}$ with an action of
$\tilde \beta _{B,\ast }\mathcal {O}_{\tilde {X}_{\check B}} =R\tilde \beta _{B,\ast }\mathcal {O}_{\tilde {X}_{\check B}}$ with an action of ![]() $\mathcal {H}_G$, depending on the choice of the Whittaker datum
$\mathcal {H}_G$, depending on the choice of the Whittaker datum ![]() $\psi$, such that
$\psi$, such that
is the desired functor in the case of ![]() $G={\rm SL}_2$. Computing the fibers of
$G={\rm SL}_2$. Computing the fibers of ![]() $\tilde \beta _{B,\ast }\mathcal {O}_{\tilde {X}_{\check B}}$, we find
$\tilde \beta _{B,\ast }\mathcal {O}_{\tilde {X}_{\check B}}$, we find
and the action of the centralizer of ![]() $x$ is trivial on
$x$ is trivial on ![]() $(\pi _{x}^{\psi \text {-}{\rm gen}})^I$ and non-trivial on
$(\pi _{x}^{\psi \text {-}{\rm gen}})^I$ and non-trivial on ![]() $(\pi _{x}^{\psi '\text {-}{\rm gen}})^I$.
$(\pi _{x}^{\psi '\text {-}{\rm gen}})^I$.
4.9 Calculation of examples
We finish by computing the image of some special representations under the functor ![]() $R_G$ defined in (4.11). In particular, we are in the situation
$R_G$ defined in (4.11). In particular, we are in the situation ![]() $G={\rm GL}_n(F)$ and
$G={\rm GL}_n(F)$ and ![]() $\check G$ is the algebraic group
$\check G$ is the algebraic group ![]() $\operatorname {GL}_n$ over
$\operatorname {GL}_n$ over ![]() $C$. For simplicity we assume that
$C$. For simplicity we assume that ![]() $C$ is algebraically closed. We fix the choice of the diagonal torus
$C$ is algebraically closed. We fix the choice of the diagonal torus ![]() $\mathbb {T}$ and the upper triangular Borel subgroup
$\mathbb {T}$ and the upper triangular Borel subgroup ![]() $\mathbb {B}$.
$\mathbb {B}$.
Let ![]() $x=(\varphi,N)\in X_{\check G}$. In the examples calculated in this section we will assume that
$x=(\varphi,N)\in X_{\check G}$. In the examples calculated in this section we will assume that ![]() $\varphi$ is regular semi-simple. As in Remark 3.3(b), we write
$\varphi$ is regular semi-simple. As in Remark 3.3(b), we write
for the ![]() $\check G$-orbit of
$\check G$-orbit of ![]() $(\varphi,N)$ and
$(\varphi,N)$ and ![]() $X_{\check G,[\varphi,N]}$ for its closure.
$X_{\check G,[\varphi,N]}$ for its closure.
Theorem 4.34 Let ![]() $(\varphi,N)\in X_{\check G}(C)$ and assume that
$(\varphi,N)\in X_{\check G}(C)$ and assume that ![]() $\varphi$ is regular semi-simple. Then
$\varphi$ is regular semi-simple. Then
To prove this, we will use compatibility with parabolic induction. Hence, the main step will be to calculate the image of the generalized Steinberg representations.
Let ![]() $\chi :\mathfrak {Z}\rightarrow C$ be the character defined by the characteristic polynomial of
$\chi :\mathfrak {Z}\rightarrow C$ be the character defined by the characteristic polynomial of ![]() $\varphi$. We write
$\varphi$. We write ![]() $\hat {\mathfrak {Z}}_\chi$ for the completion of
$\hat {\mathfrak {Z}}_\chi$ for the completion of ![]() $\mathfrak {Z}$ with respect to the kernel
$\mathfrak {Z}$ with respect to the kernel ![]() $\mathfrak {m}_\chi$ of
$\mathfrak {m}_\chi$ of ![]() $\chi$ and
$\chi$ and
for the ![]() $\mathfrak {m}_\chi$-adic completion of
$\mathfrak {m}_\chi$-adic completion of ![]() $\mathcal {H}_G$. Similarly, if
$\mathcal {H}_G$. Similarly, if ![]() $M\subset G$ is a Levi subgroup, we write
$M\subset G$ is a Levi subgroup, we write ![]() $\hat{\mathcal {H}}_{M,\chi }$ for the corresponding completion of
$\hat{\mathcal {H}}_{M,\chi }$ for the corresponding completion of ![]() $\mathcal {H}_M$.
$\mathcal {H}_M$.
Assume that ![]() $\varphi ={\rm diag}(\varphi _1,\ldots,\varphi _n)$. For
$\varphi ={\rm diag}(\varphi _1,\ldots,\varphi _n)$. For ![]() $w\in W=\mathcal {S}_n$ we write
$w\in W=\mathcal {S}_n$ we write ![]() $w\varphi$ for the diagonal matrix
$w\varphi$ for the diagonal matrix ![]() ${\rm diag}(\varphi _{w(1)},\ldots,\varphi _{w(n)})$. We use the notation
${\rm diag}(\varphi _{w(1)},\ldots,\varphi _{w(n)})$. We use the notation ![]() $\delta _w$ to denote the
$\delta _w$ to denote the ![]() $\mathcal {H}_T$-module defined by the unramified character
$\mathcal {H}_T$-module defined by the unramified character ![]() ${\rm unr}_{w\varphi }$ (i.e. the residue field at the point
${\rm unr}_{w\varphi }$ (i.e. the residue field at the point ![]() $w\varphi \in {\rm Spec}\,\mathcal {H}_T$), and
$w\varphi \in {\rm Spec}\,\mathcal {H}_T$), and ![]() $\hat \delta _w$ to denote the completion of
$\hat \delta _w$ to denote the completion of ![]() $\mathcal {H}_T$ at the point
$\mathcal {H}_T$ at the point ![]() $w\varphi \in {\operatorname {Spec}}\, \mathcal {H}_T$. Then
$w\varphi \in {\operatorname {Spec}}\, \mathcal {H}_T$. Then ![]() $\delta _w$ and
$\delta _w$ and ![]() $\hat \delta _w$ are
$\hat \delta _w$ are ![]() $\hat{\mathcal {H}}_{T,\chi }$-modules.
$\hat{\mathcal {H}}_{T,\chi }$-modules.
We recall intertwining operators for parabolic induction. Let ![]() $\mathbb {P},\mathbb {P'}\subset \mathbb {G}$ be parabolic subgroups (containing
$\mathbb {P},\mathbb {P'}\subset \mathbb {G}$ be parabolic subgroups (containing ![]() $\mathbb {T}$) with Levi subgroups
$\mathbb {T}$) with Levi subgroups ![]() $\mathbb {M}$ and
$\mathbb {M}$ and ![]() $\mathbb {M}'$ and let
$\mathbb {M}'$ and let ![]() $w\in W$ such that
$w\in W$ such that ![]() $M'=wMw^{-1}$. Let
$M'=wMw^{-1}$. Let ![]() $\pi$ (respectively,
$\pi$ (respectively, ![]() $\pi '$) be smooth representations of
$\pi '$) be smooth representations of ![]() $M$ (respectively,
$M$ (respectively, ![]() $M'$) and let
$M'$) and let ![]() $f:\pi ^w\rightarrow \pi '$ be a morphism of
$f:\pi ^w\rightarrow \pi '$ be a morphism of ![]() $M'$-representations. Then there is a canonical morphism of
$M'$-representations. Then there is a canonical morphism of ![]() $G$-representations
$G$-representations
associated to ![]() $f$ (and similarly for
$f$ (and similarly for ![]() $\iota _{P}^G$ and
$\iota _{P}^G$ and ![]() $\iota _{P'}^G$). Moreover, this construction extends to (morphisms of) complexes of
$\iota _{P'}^G$). Moreover, this construction extends to (morphisms of) complexes of ![]() $M$ (respectively,
$M$ (respectively, ![]() $M'$) representations. We also note that the formation of these intertwining operators is transitive in the following sense. Let
$M'$) representations. We also note that the formation of these intertwining operators is transitive in the following sense. Let ![]() $\mathbb {P}_1,\mathbb {P}'_1\subset \mathbb {P}\subset \mathbb {G}$ be parabolic subgroups. Let
$\mathbb {P}_1,\mathbb {P}'_1\subset \mathbb {P}\subset \mathbb {G}$ be parabolic subgroups. Let ![]() $\mathbb {M}_1,\mathbb {M}'_1$ and
$\mathbb {M}_1,\mathbb {M}'_1$ and ![]() $\mathbb {M}$ denote the corresponding Levi quotients and let
$\mathbb {M}$ denote the corresponding Levi quotients and let ![]() $\mathbb {P}_{1,M}$ be the image of
$\mathbb {P}_{1,M}$ be the image of ![]() $\mathbb {P}_1$ in
$\mathbb {P}_1$ in ![]() $\mathbb {M}$ (and similarly
$\mathbb {M}$ (and similarly ![]() $\mathbb {P}'_{1,M}$). Let
$\mathbb {P}'_{1,M}$). Let ![]() $w\in W_M\subset W$ be a Weyl group element such that
$w\in W_M\subset W$ be a Weyl group element such that ![]() $wM_1w^{-1}=M'_1$ (as subgroups of
$wM_1w^{-1}=M'_1$ (as subgroups of ![]() $G$, and hence also as subgroups of
$G$, and hence also as subgroups of ![]() $M$). Moreover, let
$M$). Moreover, let ![]() $\pi$ be a representation of
$\pi$ be a representation of ![]() $M_1$,
$M_1$, ![]() $\pi '$ be a representation of
$\pi '$ be a representation of ![]() $M'_1$, and
$M'_1$, and ![]() $f:\pi ^w\rightarrow \pi '$ be a morphism of
$f:\pi ^w\rightarrow \pi '$ be a morphism of ![]() $M'_1$-representations. Then, under the canonical identifications
$M'_1$-representations. Then, under the canonical identifications
the morphism ![]() $\iota _{\overline {P}}^G(F_M(w,f))$ is identified with
$\iota _{\overline {P}}^G(F_M(w,f))$ is identified with ![]() $F_G(w,f)$.
$F_G(w,f)$.
Now fix ![]() $\lambda \in C^\times$ and let
$\lambda \in C^\times$ and let ![]() $\varphi ={\rm diag}(\lambda, q^{-1}\lambda,\ldots, q^{-(n-1)}\lambda )$. For
$\varphi ={\rm diag}(\lambda, q^{-1}\lambda,\ldots, q^{-(n-1)}\lambda )$. For ![]() $w,w'\in W$ the identity of
$w,w'\in W$ the identity of ![]() $\delta _{w'}$ and
$\delta _{w'}$ and ![]() $\hat \delta _{w'}$, respectively, induces intertwining operators
$\hat \delta _{w'}$, respectively, induces intertwining operators
 \begin{equation} \begin{aligned} f(w,w'):\iota_{\overline{B}}^G(\delta_w) & \longrightarrow \iota_{\overline{B}}^G(\delta_{w'}),\\ \hat f(w,w'):\iota_{\overline{B}}^G(\hat\delta_w) & \longrightarrow \hat \iota_{\overline{B}}^G(\hat\delta_{w'}). \end{aligned} \end{equation}
\begin{equation} \begin{aligned} f(w,w'):\iota_{\overline{B}}^G(\delta_w) & \longrightarrow \iota_{\overline{B}}^G(\delta_{w'}),\\ \hat f(w,w'):\iota_{\overline{B}}^G(\hat\delta_w) & \longrightarrow \hat \iota_{\overline{B}}^G(\hat\delta_{w'}). \end{aligned} \end{equation}
Note that these morphisms are isomorphisms (with inverse ![]() $f(w',w)$ and
$f(w',w)$ and ![]() $\hat f(w',w)$, respectively) if and only if for each
$\hat f(w',w)$, respectively) if and only if for each ![]() $i$ the entries
$i$ the entries ![]() $q^{-i}\lambda$ and
$q^{-i}\lambda$ and ![]() $q^{-(i+1)}\lambda$ appear in the same order in
$q^{-(i+1)}\lambda$ appear in the same order in ![]() $w\varphi$ and
$w\varphi$ and ![]() $w'\varphi$. Moreover,
$w'\varphi$. Moreover,
is a free ![]() $\hat {\mathfrak {Z}}_\chi$-module of rank one. We define the (universal) deformation of the generalized Steinberg representation
$\hat {\mathfrak {Z}}_\chi$-module of rank one. We define the (universal) deformation of the generalized Steinberg representation
Here we write ![]() $\widehat {\rm unr}_\lambda$ for the universal (unramified) deformation of the character
$\widehat {\rm unr}_\lambda$ for the universal (unramified) deformation of the character ![]() ${\rm unr}_{\lambda }$ and denote the target of
${\rm unr}_{\lambda }$ and denote the target of ![]() $\widehat {\rm unr}_\lambda$ by
$\widehat {\rm unr}_\lambda$ by ![]() $C[\![t]\!]$. Then
$C[\![t]\!]$. Then
 \begin{align*} \widehat{\rm unr}_\lambda\otimes_{C[\![t]\!]}C[\![t]\!]/(t)&={\rm unr}_\lambda,\\ \hat{\rm St}(\lambda,r)\otimes_{C[\![t]\!]}C[\![t]\!]/(t)&={\rm St}(\lambda,r). \end{align*}
\begin{align*} \widehat{\rm unr}_\lambda\otimes_{C[\![t]\!]}C[\![t]\!]/(t)&={\rm unr}_\lambda,\\ \hat{\rm St}(\lambda,r)\otimes_{C[\![t]\!]}C[\![t]\!]/(t)&={\rm St}(\lambda,r). \end{align*}
Note that by definition ![]() $\hat {\rm St}(\lambda,n)$ is a quotient of
$\hat {\rm St}(\lambda,n)$ is a quotient of ![]() $\iota _{\overline {B}}^G\hat \delta _{w_0}$, where
$\iota _{\overline {B}}^G\hat \delta _{w_0}$, where ![]() $w_0\in W$ is the longest element.
$w_0\in W$ is the longest element.
By abuse of notation we will also write ![]() ${\rm St}(\lambda,n)$ (respectively,
${\rm St}(\lambda,n)$ (respectively, ![]() $\hat {\rm St}(\lambda,n)$) for the
$\hat {\rm St}(\lambda,n)$) for the ![]() $\mathcal {H}_G$-module (respectively,
$\mathcal {H}_G$-module (respectively, ![]() $\hat{\mathcal {H}}_{G,\chi }$-module) given by the
$\hat{\mathcal {H}}_{G,\chi }$-module) given by the ![]() $I$-invariants in the respective representations. Similarly, we will continue to write
$I$-invariants in the respective representations. Similarly, we will continue to write ![]() $\iota _{\overline {B}}^G\delta _w$, etc. for the Hecke modules defined by these representations. In the following we will only work with Hecke modules, hence no confusion should arise.
$\iota _{\overline {B}}^G\delta _w$, etc. for the Hecke modules defined by these representations. In the following we will only work with Hecke modules, hence no confusion should arise.
We construct a projective resolution ![]() $\hat C^\bullet _{n,\lambda }$ of the
$\hat C^\bullet _{n,\lambda }$ of the ![]() $\hat{\mathcal {H}}_{G,\chi }$-module
$\hat{\mathcal {H}}_{G,\chi }$-module ![]() $\hat {\rm St}(\lambda,n)$ concentrated in (cohomological) degrees
$\hat {\rm St}(\lambda,n)$ concentrated in (cohomological) degrees ![]() $[-(n-1),0]$ such that all objects in the complex are direct sums of induced representations
$[-(n-1),0]$ such that all objects in the complex are direct sums of induced representations ![]() ${\iota }_{\overline {B}}^G\hat \delta _w$ and the differentials are given by combinations of the intertwining morphisms (4.23). We construct the complex by induction.
${\iota }_{\overline {B}}^G\hat \delta _w$ and the differentials are given by combinations of the intertwining morphisms (4.23). We construct the complex by induction.
If ![]() $n=2$, then
$n=2$, then ![]() $\varphi ={\rm diag}(\lambda, q^{-1}\lambda )$ and we consider the complex
$\varphi ={\rm diag}(\lambda, q^{-1}\lambda )$ and we consider the complex
where ![]() $s\in \mathcal {S}_2$ is the unique non-trivial element. It can easily be checked that the morphism
$s\in \mathcal {S}_2$ is the unique non-trivial element. It can easily be checked that the morphism ![]() $\hat f(1,s)$ is injective and that its cokernel is
$\hat f(1,s)$ is injective and that its cokernel is ![]() $\hat {\rm St}(\lambda,2)$.
$\hat {\rm St}(\lambda,2)$.
Assume we have constructed ![]() $\hat C^\bullet _{n-1,\lambda }$. For
$\hat C^\bullet _{n-1,\lambda }$. For ![]() $i=1,2$ consider the upper triangular block parabolic subgroup
$i=1,2$ consider the upper triangular block parabolic subgroup ![]() $\mathbb {P}_i\subset \mathbb {G}$ with Levi subgroup
$\mathbb {P}_i\subset \mathbb {G}$ with Levi subgroup ![]() $\mathbb {M}_i$ such that
$\mathbb {M}_i$ such that ![]() $\mathbb {M}_1$ has block sizes
$\mathbb {M}_1$ has block sizes ![]() $(n-1,1)$ and
$(n-1,1)$ and ![]() $\mathbb {M}_2$ has block sizes
$\mathbb {M}_2$ has block sizes ![]() $(1,n-1)$. We consider
$(1,n-1)$. We consider
as a complex of ![]() $\hat{\mathcal {H}}_{M_1,\chi }$-modules and
$\hat{\mathcal {H}}_{M_1,\chi }$-modules and
as a complex of ![]() $\hat{\mathcal {H}}_{M_2,\chi }$-modules. Let
$\hat{\mathcal {H}}_{M_2,\chi }$-modules. Let ![]() $\sigma \in \mathcal {S}_n$ be the cycle
$\sigma \in \mathcal {S}_n$ be the cycle ![]() $(12\cdots n)$. Then
$(12\cdots n)$. Then ![]() $M_1$ and
$M_1$ and ![]() $M_2$ satisfy
$M_2$ satisfy ![]() $\sigma M_1\sigma ^{-1}=M_2$ and the identity
$\sigma M_1\sigma ^{-1}=M_2$ and the identity ![]() $(D_1^\bullet )^\sigma \rightarrow D_2^\bullet$, as a morphism of complexes of
$(D_1^\bullet )^\sigma \rightarrow D_2^\bullet$, as a morphism of complexes of ![]() $\hat{\mathcal {H}}_{M_2,\chi }$-modules, induces a morphism of complexes
$\hat{\mathcal {H}}_{M_2,\chi }$-modules, induces a morphism of complexes
We define ![]() $\hat C_{n,\lambda }^\bullet$ as the mapping cone of this complex. Then
$\hat C_{n,\lambda }^\bullet$ as the mapping cone of this complex. Then ![]() $\hat C_{n,\lambda }^\bullet$ obviously is a complex in degree
$\hat C_{n,\lambda }^\bullet$ obviously is a complex in degree ![]() $[-(n-1),0]$ whose entries are (by transitivity of parabolic induction) direct sums of
$[-(n-1),0]$ whose entries are (by transitivity of parabolic induction) direct sums of ![]() $\iota _{\overline {B}}^G(\hat \delta _w)$ for some
$\iota _{\overline {B}}^G(\hat \delta _w)$ for some ![]() $w\in W$ (each isomorphism class appearing exactly once) and the differentials are given by intertwining operators (by transitivity of intertwining operators).
$w\in W$ (each isomorphism class appearing exactly once) and the differentials are given by intertwining operators (by transitivity of intertwining operators).
Lemma 4.35 The complex ![]() $\hat C^\bullet _{n,\lambda }$ is exact in negative degrees and
$\hat C^\bullet _{n,\lambda }$ is exact in negative degrees and
Proof. We proceed by induction. If ![]() $n=2$ this was already remarked above. Assume that
$n=2$ this was already remarked above. Assume that ![]() $\hat C^\bullet _{n-1,\lambda }$ is quasi-isomorphic to
$\hat C^\bullet _{n-1,\lambda }$ is quasi-isomorphic to ![]() $\hat {\rm St}(\lambda,n-1)$. Then
$\hat {\rm St}(\lambda,n-1)$. Then ![]() $\hat C^\bullet _{n,\lambda }$ is quasi-isomorphic to the complex
$\hat C^\bullet _{n,\lambda }$ is quasi-isomorphic to the complex
in degrees ![]() $-1$ and
$-1$ and ![]() $0$, where the morphism is given by the obvious intertwining map. One can easily check that this morphism is injective and its cokernel is
$0$, where the morphism is given by the obvious intertwining map. One can easily check that this morphism is injective and its cokernel is ![]() $\hat {\rm St}(\lambda,n)$.
$\hat {\rm St}(\lambda,n)$.
Similarly to the definition of ![]() $\hat{\mathcal {H}}_{G,\chi }$, we define
$\hat{\mathcal {H}}_{G,\chi }$, we define ![]() $\mathfrak {m}_\chi$-adic completions on the side of stacks of L-parameters. Let
$\mathfrak {m}_\chi$-adic completions on the side of stacks of L-parameters. Let ![]() $\hat X_{\check G,\chi }$ denote the completion of
$\hat X_{\check G,\chi }$ denote the completion of ![]() $X_{\check G}$ along the pre-image of
$X_{\check G}$ along the pre-image of ![]() $\chi \in {\rm Spec}\,\mathfrak {Z}=\check T/W$ under the canonical morphism
$\chi \in {\rm Spec}\,\mathfrak {Z}=\check T/W$ under the canonical morphism ![]() $X_{\check G}\rightarrow \check T/W$. This formal scheme is still equipped with an action of
$X_{\check G}\rightarrow \check T/W$. This formal scheme is still equipped with an action of ![]() $\check G$ and we can form the stack quotient
$\check G$ and we can form the stack quotient ![]() $[\hat X_{\check G,\chi }/\check G]$. Similarly, we write
$[\hat X_{\check G,\chi }/\check G]$. Similarly, we write ![]() $\hat X_{\check P,\chi }$ and
$\hat X_{\check P,\chi }$ and ![]() $\hat X_{\check M,\chi }$ for the corresponding completions of
$\hat X_{\check M,\chi }$ for the corresponding completions of ![]() $X_{\check P}$ and
$X_{\check P}$ and ![]() $X_{\check M}$. The functor
$X_{\check M}$. The functor ![]() $R_G$ defined in (4.11) naturally extends to a functor
$R_G$ defined in (4.11) naturally extends to a functor
As a consequence of Theorem 4.25 the functor ![]() $\hat R_{G,\chi }$ also satisfies compatibility with parabolic induction similarly to Conjecture 3.2(ii), but for the induced morphism between the formal completions of the stacks involved.
$\hat R_{G,\chi }$ also satisfies compatibility with parabolic induction similarly to Conjecture 3.2(ii), but for the induced morphism between the formal completions of the stacks involved.
Let us build a more explicit model of these stacks. We consider the closed formal subscheme
where ![]() $C[u_1,\ldots,u_{n-1}][\![t_1,\ldots,t_n]\!]/((t_{i+1}-t_i)u_i)$ is equipped with the
$C[u_1,\ldots,u_{n-1}][\![t_1,\ldots,t_n]\!]/((t_{i+1}-t_i)u_i)$ is equipped with the ![]() $(t_1,\ldots,t_n)$-adic topology. The embedding into
$(t_1,\ldots,t_n)$-adic topology. The embedding into ![]() $\hat X_{\check G,\chi }$ is defined by the
$\hat X_{\check G,\chi }$ is defined by the ![]() $(\varphi,N)$-module
$(\varphi,N)$-module
 \begin{align*} \varphi_{\hat Y}&={\rm diag}(\lambda+t_1,q^{-1}(\lambda+t_2),\ldots, q^{-(n-1)}(\lambda+t_n)),\\ N_{\hat Y}(e_i)&=\begin{cases} u_ie_{i+1}, & i< n-1,\\ 0, & i=n-1, \end{cases} \end{align*}
\begin{align*} \varphi_{\hat Y}&={\rm diag}(\lambda+t_1,q^{-1}(\lambda+t_2),\ldots, q^{-(n-1)}(\lambda+t_n)),\\ N_{\hat Y}(e_i)&=\begin{cases} u_ie_{i+1}, & i< n-1,\\ 0, & i=n-1, \end{cases} \end{align*}
over ![]() $\hat Y$. This formal scheme comes equipped with a canonical
$\hat Y$. This formal scheme comes equipped with a canonical ![]() $\check T$-action (which is trivial on the
$\check T$-action (which is trivial on the ![]() $t_i$ and via the adjoint action on the
$t_i$ and via the adjoint action on the ![]() $u_i$) such that
$u_i$) such that ![]() $[\hat Y/\check T]=[\hat X_{\check G,\chi }/\check G]$.
$[\hat Y/\check T]=[\hat X_{\check G,\chi }/\check G]$.
For ![]() $w\in W$ we define a closed
$w\in W$ we define a closed ![]() $\check T$-equivariant formal subscheme
$\check T$-equivariant formal subscheme ![]() $\hat Y(w)$ by adding the equation
$\hat Y(w)$ by adding the equation ![]() $u_i=0$ if
$u_i=0$ if ![]() $q^{-(i-1)}\lambda$ precedes
$q^{-(i-1)}\lambda$ precedes ![]() $q^{-i}\lambda$ in
$q^{-i}\lambda$ in ![]() $w\varphi$. In particular,
$w\varphi$. In particular, ![]() $\hat Y({w_0})=\hat Y$ if
$\hat Y({w_0})=\hat Y$ if ![]() $w_0\in W$ is the longest element. We denote by
$w_0\in W$ is the longest element. We denote by ![]() $\hat X_{\check G,\chi }(w)$ the corresponding
$\hat X_{\check G,\chi }(w)$ the corresponding ![]() $\check G$-equivariant closed formal subscheme of
$\check G$-equivariant closed formal subscheme of ![]() $\hat X_{\check G,\chi }$.
$\hat X_{\check G,\chi }$.
Lemma 4.36 There is an isomorphism
where we view ![]() $\hat R_{G,\chi }(\iota _{\overline {B}}^G\hat \delta _w)$ as a
$\hat R_{G,\chi }(\iota _{\overline {B}}^G\hat \delta _w)$ as a ![]() $\check G$-equivariant sheaf on
$\check G$-equivariant sheaf on ![]() $\hat X_{\check G,\chi }$.
$\hat X_{\check G,\chi }$.
Proof. This is a straightforward calculation using the compatibility of ![]() $\hat R_{G,\chi }$ with parabolic induction.
$\hat R_{G,\chi }$ with parabolic induction.
The lemma identifies the images of parabolically induced representations under ![]() $\hat R_{G,\chi }$. Next we identify the images of intertwining operators. For
$\hat R_{G,\chi }$. Next we identify the images of intertwining operators. For ![]() $w,w'\in W$ there is a canonical
$w,w'\in W$ there is a canonical ![]() $\check T$-equivariant morphism
$\check T$-equivariant morphism
defined as follows. Let ![]() $I_w=\{i=1,\ldots, n-1|\ q^{-(i-1)}\lambda\ \text {precedes}\ q^{-i}\lambda \ \text {in}\ w\varphi \}$, that is,
$I_w=\{i=1,\ldots, n-1|\ q^{-(i-1)}\lambda\ \text {precedes}\ q^{-i}\lambda \ \text {in}\ w\varphi \}$, that is,
and let us write
for the moment. Then, similarly to (4.18), multiplication by ![]() $\prod _{i\in I_w\backslash I_{w'}} (t_{i+1}-t_i)$ induces a morphism
$\prod _{i\in I_w\backslash I_{w'}} (t_{i+1}-t_i)$ induces a morphism ![]() $\mathcal {O}_{\hat Y(w)}\rightarrow \mathcal {O}_{\hat Y(w,w')}$ and we define
$\mathcal {O}_{\hat Y(w)}\rightarrow \mathcal {O}_{\hat Y(w,w')}$ and we define ![]() $\hat g(w,w')$ to be its composition with the canonical projection to
$\hat g(w,w')$ to be its composition with the canonical projection to ![]() $\mathcal {O}_{\hat Y(w')}$.
$\mathcal {O}_{\hat Y(w')}$.
Lemma 4.37 For ![]() $w,w'\in W$ the
$w,w'\in W$ the ![]() $\hat {\mathfrak {Z}}_\chi$-module
$\hat {\mathfrak {Z}}_\chi$-module
is free of rank one with basis ![]() $\hat g(w,w')$.
$\hat g(w,w')$.
Proof. This is a straightforward computation.
By the following theorem the images of the intertwining operators ![]() $\hat R_{G,\chi }(\hat f(w,w'))$ can be identified (up to isomorphism) with the morphisms
$\hat R_{G,\chi }(\hat f(w,w'))$ can be identified (up to isomorphism) with the morphisms ![]() $\hat g(w,w')$ just constructed.
$\hat g(w,w')$ just constructed.
Theorem 4.38 Let ![]() $\varphi ={\rm diag}(\lambda,q^{-1}\lambda,\ldots, q^{-(n-1)}\lambda )\in \check T(C)$ and
$\varphi ={\rm diag}(\lambda,q^{-1}\lambda,\ldots, q^{-(n-1)}\lambda )\in \check T(C)$ and ![]() $\chi :\mathfrak {Z}\rightarrow C$ be the character defined by the image of
$\chi :\mathfrak {Z}\rightarrow C$ be the character defined by the image of ![]() $\varphi$ in
$\varphi$ in ![]() $\check T/W$. The set of functors
$\check T/W$. The set of functors
for standard Levi subgroups ![]() $M\subset G$, is uniquely determined (up to isomorphism) by requiring that they are
$M\subset G$, is uniquely determined (up to isomorphism) by requiring that they are ![]() $\hat {\mathfrak {Z}}_{M,\chi }$-linear, compatible with parabolic induction, and that
$\hat {\mathfrak {Z}}_{M,\chi }$-linear, compatible with parabolic induction, and that ![]() $\hat R_{T,\chi }$ is induced by the identification
$\hat R_{T,\chi }$ is induced by the identification
More precisely, let ![]() $\hat R'_{G,\chi }$ be any functor satisfying these conditions. Then for each
$\hat R'_{G,\chi }$ be any functor satisfying these conditions. Then for each ![]() $w\in W$, there are isomorphisms
$w\in W$, there are isomorphisms
such that for ![]() $w,w'\in W$ the diagram
$w,w'\in W$ the diagram

commutes.
Remark 4.39 (a) Note that we do not need to add the requirement
which also would be a consequence of the requirements in Conjecture 3.2. In the situation considered here, there is an isomorphism
and hence the above isomorphism is automatic.
(b) It seems possible to compute that
for ![]() $w,w'\in W$ and
$w,w'\in W$ and ![]() $i\neq 0$ by a similar explicit computation to that in Proposition 4.31. This would imply the conjectured full faithfulness of
$i\neq 0$ by a similar explicit computation to that in Proposition 4.31. This would imply the conjectured full faithfulness of ![]() $\hat R_{G,\chi }$.
$\hat R_{G,\chi }$.
Proof. Let us first justify that the second assertion implies the first. Note that
 \[ \hat{\mathcal{H}}_{M,\chi}=\hat{\mathcal{H}}_{M,\chi}\otimes_{\hat{\mathcal{H}}_{T,\chi}} \hat{\mathcal{H}}_{T,\chi}=\hat{\mathcal{H}}_{M,\chi}\otimes_{\hat{\mathcal{H}}_{T,\chi}} \bigg(\bigoplus_{w\in W_M} \hat\delta_w\bigg)=\bigoplus_{w\in W_M}\iota_{\overline{B}_M}^M\hat\delta_w. \]
\[ \hat{\mathcal{H}}_{M,\chi}=\hat{\mathcal{H}}_{M,\chi}\otimes_{\hat{\mathcal{H}}_{T,\chi}} \hat{\mathcal{H}}_{T,\chi}=\hat{\mathcal{H}}_{M,\chi}\otimes_{\hat{\mathcal{H}}_{T,\chi}} \bigg(\bigoplus_{w\in W_M} \hat\delta_w\bigg)=\bigoplus_{w\in W_M}\iota_{\overline{B}_M}^M\hat\delta_w. \]
Using free resolutions of bounded-above objects in ![]() $\mathbf {D}^+(\hat{\mathcal {H}}_{M,\chi }\text {-mod})$, it is hence enough control the images of parabolically induced representations and the images of the intertwining operators. Then a limit argument deals with the general case.
$\mathbf {D}^+(\hat{\mathcal {H}}_{M,\chi }\text {-mod})$, it is hence enough control the images of parabolically induced representations and the images of the intertwining operators. Then a limit argument deals with the general case.
Given ![]() $\hat R'_{G,\chi }$ as in the formulation of the theorem, compatibility with parabolic induction forces the existence of isomorphisms
$\hat R'_{G,\chi }$ as in the formulation of the theorem, compatibility with parabolic induction forces the existence of isomorphisms ![]() $\alpha _w$. Note that
$\alpha _w$. Note that ![]() $\alpha _w$ is unique up to a unit in
$\alpha _w$ is unique up to a unit in ![]() $\hat {\mathfrak {Z}}_\chi$. We claim that we can choose the isomorphisms such that the diagrams (4.26) are commutative. In order to do so, we proceed by induction. By assumption the claim is true for
$\hat {\mathfrak {Z}}_\chi$. We claim that we can choose the isomorphisms such that the diagrams (4.26) are commutative. In order to do so, we proceed by induction. By assumption the claim is true for ![]() $n=1$. We also make
$n=1$. We also make ![]() $n=2$ explicit. In this case we can identify
$n=2$ explicit. In this case we can identify
One calculates that the intertwining operators ![]() $\hat f(1,s)$ and
$\hat f(1,s)$ and ![]() $\hat f(s,1)$ are identified with a
$\hat f(s,1)$ are identified with a ![]() $\hat {\mathfrak {Z}}_\chi$-basis of
$\hat {\mathfrak {Z}}_\chi$-basis of
respectively. Moreover, the compositions ![]() $\hat f(1,s)\circ \hat f(s,1)$ and
$\hat f(1,s)\circ \hat f(s,1)$ and ![]() $\hat f(s,1)\circ \hat f(1,s)$ are the multiplications with
$\hat f(s,1)\circ \hat f(1,s)$ are the multiplications with ![]() $f\in \hat {\mathfrak {Z}}^\times _\chi$, with
$f\in \hat {\mathfrak {Z}}^\times _\chi$, with ![]() $f$ as defined just before Proposition 4.31. The calculation in the rank-two case, Proposition 4.31, yields the claim.
$f$ as defined just before Proposition 4.31. The calculation in the rank-two case, Proposition 4.31, yields the claim.
Assume now that the claim is true for ![]() $n-1$ and view
$n-1$ and view ![]() $\mathcal {S}_{n-1}$ as the subgroup of
$\mathcal {S}_{n-1}$ as the subgroup of ![]() $W=\mathcal {S}_n$ permuting the elements
$W=\mathcal {S}_n$ permuting the elements ![]() $1,\ldots, n-1$. Recall the parabolic subgroups
$1,\ldots, n-1$. Recall the parabolic subgroups ![]() $P_1$ and
$P_1$ and ![]() $P_2$ from the inductive construction of the complex
$P_2$ from the inductive construction of the complex ![]() $\hat C^\bullet _{n,\lambda }$. Using parabolic induction
$\hat C^\bullet _{n,\lambda }$. Using parabolic induction ![]() $\iota _{\overline {P}_1}^G$ and the induction hypothesis, we may assume that we have constructed
$\iota _{\overline {P}_1}^G$ and the induction hypothesis, we may assume that we have constructed ![]() $\alpha _w$ for all
$\alpha _w$ for all ![]() $w\in \mathcal {S}_{n-1}\subset W$ such that the diagram (4.26) commutes for all
$w\in \mathcal {S}_{n-1}\subset W$ such that the diagram (4.26) commutes for all ![]() $w,w'\in \mathcal {S}_{n-1}$. Let
$w,w'\in \mathcal {S}_{n-1}$. Let ![]() $\sigma =(12\cdots n)$ as above. We first show that we can choose
$\sigma =(12\cdots n)$ as above. We first show that we can choose
such that (4.26) commutes for the pairs ![]() $w,\sigma w\sigma ^{-1}$ and
$w,\sigma w\sigma ^{-1}$ and ![]() $\sigma w \sigma ^{-1},w$. Let
$\sigma w \sigma ^{-1},w$. Let ![]() $\tau _{i,i+1}$ denote the transposition of
$\tau _{i,i+1}$ denote the transposition of ![]() $i$ and
$i$ and ![]() $i+1$. Inductively we define
$i+1$. Inductively we define ![]() $w_1=\tau _{n,n-1}w\tau _{n,n-1}$ and
$w_1=\tau _{n,n-1}w\tau _{n,n-1}$ and ![]() $w_i=\tau _{n-i,n-i-1}w_{i-1}\tau _{n-i,n-i-1}$. Then the composition of intertwining operators
$w_i=\tau _{n-i,n-i-1}w_{i-1}\tau _{n-i,n-i-1}$. Then the composition of intertwining operators
is identified with ![]() $\beta \hat f(w,\sigma w \sigma ^{-1})$ for some
$\beta \hat f(w,\sigma w \sigma ^{-1})$ for some ![]() $\beta \in \hat {\mathfrak {Z}}_\chi ^\times$. Similarly, the composition
$\beta \in \hat {\mathfrak {Z}}_\chi ^\times$. Similarly, the composition
is identified with ![]() $\beta \hat f(\sigma w \sigma ^{-1},w)$ for the same unit
$\beta \hat f(\sigma w \sigma ^{-1},w)$ for the same unit ![]() $\beta$. In this composition all the intertwining maps are isomorphisms, except for the morphisms
$\beta$. In this composition all the intertwining maps are isomorphisms, except for the morphisms
where the position of ![]() $n$ and
$n$ and ![]() $n-1$ in
$n-1$ in ![]() $(w_i(1),\ldots, w_i(n))$ and
$(w_i(1),\ldots, w_i(n))$ and ![]() $(w_{i+1}(1),\ldots, w_{i+1}(n))$ is interchanged. By the computation in the two-dimensional case and compatibility with parabolic induction this intertwining morphism is given by the multiplication with
$(w_{i+1}(1),\ldots, w_{i+1}(n))$ is interchanged. By the computation in the two-dimensional case and compatibility with parabolic induction this intertwining morphism is given by the multiplication with ![]() $\beta '(t_n-t_{n-1})$ for some unit
$\beta '(t_n-t_{n-1})$ for some unit ![]() $\beta '\in \hat {\mathfrak {Z}}_\chi ^\times$ or by canonical projection multiplied with
$\beta '\in \hat {\mathfrak {Z}}_\chi ^\times$ or by canonical projection multiplied with ![]() $\beta '$. Modifying
$\beta '$. Modifying ![]() $\alpha _{\sigma w\sigma ^{-1}}$ by
$\alpha _{\sigma w\sigma ^{-1}}$ by ![]() $(\beta \beta ')^{-1}$, we deduce the commutativity of the diagrams (4.26) for the pairs
$(\beta \beta ')^{-1}$, we deduce the commutativity of the diagrams (4.26) for the pairs ![]() $w,\sigma w\sigma ^{-1}$ and
$w,\sigma w\sigma ^{-1}$ and ![]() $\sigma w \sigma ^{-1},w$.
$\sigma w \sigma ^{-1},w$.
Now consider the general case. Note that for any ![]() $w\in W$ there exists
$w\in W$ there exists ![]() $\tilde w\in \mathcal {S}_{n-1}$ such that
$\tilde w\in \mathcal {S}_{n-1}$ such that
Hence, we can choose ![]() $\alpha _w$ such that all the diagrams (4.26) commute, provided we can check commutativity of these diagrams for
$\alpha _w$ such that all the diagrams (4.26) commute, provided we can check commutativity of these diagrams for ![]() $w,w'\in \mathcal {S}_{n-1}\cup \sigma \mathcal {S}_{n-1}\sigma ^{-1}$. If both elements
$w,w'\in \mathcal {S}_{n-1}\cup \sigma \mathcal {S}_{n-1}\sigma ^{-1}$. If both elements ![]() $w,w'$ lie in
$w,w'$ lie in ![]() $\mathcal {S}_{n-1}$, this follows from the induction hypothesis. Let us check the claim for
$\mathcal {S}_{n-1}$, this follows from the induction hypothesis. Let us check the claim for ![]() $w,w''\in \mathcal {S}_{n-1}$ and
$w,w''\in \mathcal {S}_{n-1}$ and ![]() $w'=\sigma w''\sigma ^{-1}$ (the argument in the other cases being similar). By
$w'=\sigma w''\sigma ^{-1}$ (the argument in the other cases being similar). By ![]() $\hat {\mathfrak {Z}}_{\chi }$-linearity it is enough to check that
$\hat {\mathfrak {Z}}_{\chi }$-linearity it is enough to check that

commutes for any choice of ![]() $0\neq \gamma \in \hat {\mathfrak {Z}}_\chi$. In particular, we may check it for the element
$0\neq \gamma \in \hat {\mathfrak {Z}}_\chi$. In particular, we may check it for the element ![]() $\gamma$ defined by
$\gamma$ defined by
This follows from functoriality and the cases already treated above.
We now continue to calculate the image ![]() $\hat R_{G,\chi }(\hat {\rm St}(\lambda,n))$ of the deformed Steinberg representation. Let us write
$\hat R_{G,\chi }(\hat {\rm St}(\lambda,n))$ of the deformed Steinberg representation. Let us write
for the formal subscheme defined by ![]() $t:=t_1=\cdots =t_n$. We write
$t:=t_1=\cdots =t_n$. We write ![]() $\hat X_{\check G,\chi }^{\rm St}$ for the corresponding
$\hat X_{\check G,\chi }^{\rm St}$ for the corresponding ![]() $\check G$-equivariant scheme.
$\check G$-equivariant scheme.
We inductively construct a ![]() $\check T$-equivariant resolution
$\check T$-equivariant resolution ![]() $\hat E^\bullet _{n,\lambda }$ of
$\hat E^\bullet _{n,\lambda }$ of ![]() $\mathcal {O}_{\hat Y^{\rm St}}$.
$\mathcal {O}_{\hat Y^{\rm St}}$.
(i) If ![]() $n=2$ we set
$n=2$ we set
where again ![]() $s\in \mathcal {S}_2$ is the unique non-trivial element. It can easily be checked that this morphism is injective and its cokernel is
$s\in \mathcal {S}_2$ is the unique non-trivial element. It can easily be checked that this morphism is injective and its cokernel is ![]() $\mathcal {O}_{\hat Y^{\rm St}}$
$\mathcal {O}_{\hat Y^{\rm St}}$
(ii) Assume that ![]() $\hat E_{n-1,\lambda }^\bullet$ is constructed, then consider the morphism of complexes
$\hat E_{n-1,\lambda }^\bullet$ is constructed, then consider the morphism of complexes
on ![]() $\hat Y$ and define
$\hat Y$ and define ![]() $\hat E^\bullet _{n,\lambda }$ to be its mapping cone. Here we write
$\hat E^\bullet _{n,\lambda }$ to be its mapping cone. Here we write
and
by a slight abuse of notation, where we write
Lemma 4.40 The complex ![]() $\hat E^\bullet _{n,\lambda }$ is exact in negative degrees and
$\hat E^\bullet _{n,\lambda }$ is exact in negative degrees and
Proof. We proceed by induction. For ![]() $n=2$ the claim is clear. Assume the claim is true for
$n=2$ the claim is clear. Assume the claim is true for ![]() $n-1$. Then the long exact cohomology sequence implies that
$n-1$. Then the long exact cohomology sequence implies that ![]() $\hat E^\bullet _{n,\lambda }$ is quasi-isomorphic to the complex
$\hat E^\bullet _{n,\lambda }$ is quasi-isomorphic to the complex
sending ![]() $1$ to
$1$ to ![]() $(t_n-t)$. The claim follows from this.
$(t_n-t)$. The claim follows from this.
Let us denote by ![]() $\hat {\mathcal {E}}_{n,\lambda }^\bullet$ the
$\hat {\mathcal {E}}_{n,\lambda }^\bullet$ the ![]() $\check G$-equivariant complex on
$\check G$-equivariant complex on ![]() $\hat X_{\check G,\chi }$ corresponding to the
$\hat X_{\check G,\chi }$ corresponding to the ![]() $\check T$-equivariant complex
$\check T$-equivariant complex ![]() $\hat E^\bullet _{n,\lambda }$ under the identification
$\hat E^\bullet _{n,\lambda }$ under the identification ![]() $[\hat Y/\check T]=[\hat X_{\check G,\chi }/\check G]$.
$[\hat Y/\check T]=[\hat X_{\check G,\chi }/\check G]$.
Corollary 4.41 There is an isomorphism of complexes
Proof. We prove this using the inductive construction of both complexes. The case ![]() $n=1$ is trivial. Assume now that (4.27) is true for
$n=1$ is trivial. Assume now that (4.27) is true for ![]() $n-1$. Recall the parabolic subgroups
$n-1$. Recall the parabolic subgroups ![]() $P_1$ and
$P_1$ and ![]() $P_2$ from the inductive construction of
$P_2$ from the inductive construction of ![]() $\hat C^\bullet _{n,\lambda }$.
$\hat C^\bullet _{n,\lambda }$.
Let us write ![]() $G_{n-1}=\operatorname {GL}_{n-1}(F)$ and
$G_{n-1}=\operatorname {GL}_{n-1}(F)$ and ![]() $B_{n-1}\subset G_{n-1}$ for the upper triangular Borel. Further, let
$B_{n-1}\subset G_{n-1}$ for the upper triangular Borel. Further, let ![]() $\varphi '={\rm diag}(\lambda,q^{-1}\lambda,\ldots, q^{-(n-2)}\lambda )$. Similarly to the definition of
$\varphi '={\rm diag}(\lambda,q^{-1}\lambda,\ldots, q^{-(n-2)}\lambda )$. Similarly to the definition of ![]() $\delta _w$ and
$\delta _w$ and ![]() $\hat \delta _w$, using
$\hat \delta _w$, using ![]() $w\varphi$, we define
$w\varphi$, we define ![]() $\delta '_w$ and
$\delta '_w$ and ![]() $\hat \delta '_w$ using
$\hat \delta '_w$ using ![]() $w\varphi '$ for
$w\varphi '$ for ![]() $w\in \mathcal {S}_{n-1}$. Then
$w\in \mathcal {S}_{n-1}$. Then
 \begin{align*}
\iota_{\overline{P}_1}^G(\iota_{\overline{B}_{n-1}}^{G_{n-1}}
\hat\delta'_w\widehat\otimes\, \widehat{\rm
unr}_{q^{-(n-1)}\lambda})&=\iota_{\overline{B}}^G\hat\delta_w,\\
\iota_{\overline{P}_2}^G(\widehat{\rm
unr}_{q^{-(n-1)}}\widehat\otimes \,\iota_{\overline{B}_{n-1}}^{G_{n-1}}
\hat\delta'_w\lambda)&=
\iota_{\overline{B}}^G\hat\delta_{\sigma w\sigma^{-1}},
\end{align*}
\begin{align*}
\iota_{\overline{P}_1}^G(\iota_{\overline{B}_{n-1}}^{G_{n-1}}
\hat\delta'_w\widehat\otimes\, \widehat{\rm
unr}_{q^{-(n-1)}\lambda})&=\iota_{\overline{B}}^G\hat\delta_w,\\
\iota_{\overline{P}_2}^G(\widehat{\rm
unr}_{q^{-(n-1)}}\widehat\otimes \,\iota_{\overline{B}_{n-1}}^{G_{n-1}}
\hat\delta'_w\lambda)&=
\iota_{\overline{B}}^G\hat\delta_{\sigma w\sigma^{-1}},
\end{align*}
and the intertwining operator between the representations on the right-hand side translates to the intertwining operator ![]() $\hat f(w,\sigma w\sigma ^{-1})$ under this identification.
$\hat f(w,\sigma w\sigma ^{-1})$ under this identification.
By the same inductive construction, we assume that each entry of ![]() $\hat C^\bullet _{n-1,\lambda }$ is a direct sum of representations
$\hat C^\bullet _{n-1,\lambda }$ is a direct sum of representations ![]() $\iota _{\overline {B}_{n-1}}^{G_{n-1}}\hat \delta '_w$ for
$\iota _{\overline {B}_{n-1}}^{G_{n-1}}\hat \delta '_w$ for ![]() $w\in \mathcal {S}_{n-1}$. By Theorem 4.38 the morphism
$w\in \mathcal {S}_{n-1}$. By Theorem 4.38 the morphism
is (up to a unit) identified with the multiplication by ![]() $(t_n-t_{n-1})$. The inductive construction of
$(t_n-t_{n-1})$. The inductive construction of ![]() $\hat E^\bullet _{n,\lambda }$ hence implies the claim.
$\hat E^\bullet _{n,\lambda }$ hence implies the claim.
Corollary 4.42 Let ![]() $\lambda \in C^\times$ and let
$\lambda \in C^\times$ and let ![]() $(\varphi,N)\in X_{\check G}(C)$ be the L-parameter defined by
$(\varphi,N)\in X_{\check G}(C)$ be the L-parameter defined by ![]() $(C^n,\varphi,N)={\rm Sp}(\lambda,n)$. Then
$(C^n,\varphi,N)={\rm Sp}(\lambda,n)$. Then
where ![]() ${\rm St}(\lambda,n)={\rm LL}(\varphi,N)={\rm LL^{mod}}(\varphi,N)$ is the generalized Steinberg representation.
${\rm St}(\lambda,n)={\rm LL}(\varphi,N)={\rm LL^{mod}}(\varphi,N)$ is the generalized Steinberg representation.
Proof. The corollary above implies
as ![]() $\check G$-equivariant sheaves. Moreover, we have
$\check G$-equivariant sheaves. Moreover, we have
 \begin{align*} \hat{\rm St}(\lambda,n)\otimes^L_{C[\![t]\!]}C[\![t]\!]/(t)&=\hat{\rm St}(\lambda,n) \otimes_{C[\![t]\!]}C[\![t]\!]/(t)={\rm St}(\lambda,n),\\ \mathcal{O}_{\hat X_{\check G,\chi}^{\rm St}}\otimes^L_{C[\![t]\!]}C[\![t]\!]/(t)&= \mathcal{O}_{\hat X_{\check G,\chi}^{\rm St}}\otimes_{C[\![t]\!]}C[\![t]\!]/(t)=\mathcal{O}_{X_{\check G,[\varphi,N]}}. \end{align*}
\begin{align*} \hat{\rm St}(\lambda,n)\otimes^L_{C[\![t]\!]}C[\![t]\!]/(t)&=\hat{\rm St}(\lambda,n) \otimes_{C[\![t]\!]}C[\![t]\!]/(t)={\rm St}(\lambda,n),\\ \mathcal{O}_{\hat X_{\check G,\chi}^{\rm St}}\otimes^L_{C[\![t]\!]}C[\![t]\!]/(t)&= \mathcal{O}_{\hat X_{\check G,\chi}^{\rm St}}\otimes_{C[\![t]\!]}C[\![t]\!]/(t)=\mathcal{O}_{X_{\check G,[\varphi,N]}}. \end{align*}
The center ![]() $\hat {\mathfrak {Z}}_\chi$ acts on
$\hat {\mathfrak {Z}}_\chi$ acts on ![]() $\hat {\rm St}(\lambda,n)$ and
$\hat {\rm St}(\lambda,n)$ and ![]() $\mathcal {O}_{\hat X_{\check G,\chi }^{\rm St}}$ via a surjection
$\mathcal {O}_{\hat X_{\check G,\chi }^{\rm St}}$ via a surjection
Choosing a pre-image ![]() $g$ of
$g$ of ![]() $t$, we obtain isomorphisms
$t$, we obtain isomorphisms
 \begin{align*} \hat{\rm St}(\lambda,n)\otimes^L_{C[\![t]\!]}C[\![t]\!]/(t)&=\hat{\rm St}(\lambda,n) \otimes^L_{\hat{\mathfrak{Z}}_\chi}\hat{\mathfrak{Z}}_\chi/(g),\\ \mathcal{O}_{\hat X_{\check G,\chi}^{\rm St}}\otimes^L_{C[\![t]\!]}C[\![t]\!]/(t)&= \mathcal{O}_{\hat X_{\check G,\chi}^{\rm St}}\otimes^L_{\hat{\mathfrak{Z}}_\chi}\hat{\mathfrak{Z}}_\chi/(g). \end{align*}
\begin{align*} \hat{\rm St}(\lambda,n)\otimes^L_{C[\![t]\!]}C[\![t]\!]/(t)&=\hat{\rm St}(\lambda,n) \otimes^L_{\hat{\mathfrak{Z}}_\chi}\hat{\mathfrak{Z}}_\chi/(g),\\ \mathcal{O}_{\hat X_{\check G,\chi}^{\rm St}}\otimes^L_{C[\![t]\!]}C[\![t]\!]/(t)&= \mathcal{O}_{\hat X_{\check G,\chi}^{\rm St}}\otimes^L_{\hat{\mathfrak{Z}}_\chi}\hat{\mathfrak{Z}}_\chi/(g). \end{align*}
The claim now follows from ![]() $\hat {\mathfrak {Z}}_\chi$-linearity of
$\hat {\mathfrak {Z}}_\chi$-linearity of ![]() $\hat R_{G,\chi }$.
$\hat R_{G,\chi }$.
Remark 4.43 With some extra effort one can use a similar strategy to compute the images of ![]() ${\rm LL}(\varphi,N)$, where
${\rm LL}(\varphi,N)$, where ![]() $\varphi ={\rm diag}(\lambda,q^{-1}\lambda,\ldots, q^{-(n-1)}\lambda )$ and
$\varphi ={\rm diag}(\lambda,q^{-1}\lambda,\ldots, q^{-(n-1)}\lambda )$ and ![]() $N$ is an arbitrary endomorphism such that
$N$ is an arbitrary endomorphism such that ![]() $(\varphi,N)\in X_{\check G}$. Recall that
$(\varphi,N)\in X_{\check G}$. Recall that ![]() ${\rm LL}(\varphi,N)$ is the unique simple quotient of
${\rm LL}(\varphi,N)$ is the unique simple quotient of ![]() ${\rm LL^{mod}}(\varphi,N)$. One needs to build a complex similar to
${\rm LL^{mod}}(\varphi,N)$. One needs to build a complex similar to ![]() $\hat C^\bullet _{n,\lambda }$ which is a resolution of
$\hat C^\bullet _{n,\lambda }$ which is a resolution of ![]() ${\rm LL}(\varphi,N)$. We omit the technical computation, and only describe the result.
${\rm LL}(\varphi,N)$. We omit the technical computation, and only describe the result.
Let us choose such ![]() $y=(\varphi,N)\in Y\subset X_{\check G}$, where
$y=(\varphi,N)\in Y\subset X_{\check G}$, where ![]() $Y\subset \hat Y$ is the closed subscheme
$Y\subset \hat Y$ is the closed subscheme ![]() $t_1=\cdots =t_n=0$. We denote by
$t_1=\cdots =t_n=0$. We denote by ![]() $L(y)$ the sheaf of ideals defining the closed subscheme
$L(y)$ the sheaf of ideals defining the closed subscheme
Obviously this is a ![]() $\check T$-equivariant line bundle, and we write
$\check T$-equivariant line bundle, and we write ![]() $\mathcal {L}(y)$ for the corresponding
$\mathcal {L}(y)$ for the corresponding ![]() $\check G$-equivariant line bundle on
$\check G$-equivariant line bundle on ![]() $X_{\check G}$. Let us denote the number of
$X_{\check G}$. Let us denote the number of ![]() $i\in \{1,\ldots, n-1\}$ such that
$i\in \{1,\ldots, n-1\}$ such that ![]() $u_i(y)=0$ by
$u_i(y)=0$ by ![]() $l_y$. Then
$l_y$. Then
is the equivariant line bundle ![]() $\mathcal {L}(y)$ shifted to (cohomological) degree
$\mathcal {L}(y)$ shifted to (cohomological) degree ![]() $-l_y$.
$-l_y$.
Proof of Theorem 4.34 We assume that ![]() $\varphi$ is an arbitrary regular semi-simple element and choose a decomposition
$\varphi$ is an arbitrary regular semi-simple element and choose a decomposition
 \[ (C^n,\varphi,N)=\bigoplus_{i=1}^s {\rm Sp}(\lambda_i,r_i) \]
\[ (C^n,\varphi,N)=\bigoplus_{i=1}^s {\rm Sp}(\lambda_i,r_i) \]
as in § 4.1. Then
with the ordering of (4.2). Here ![]() $P$ is a block upper triangular parabolic with Levi
$P$ is a block upper triangular parabolic with Levi ![]() $M$ and we set
$M$ and we set ![]() $P'$ to be the block upper triangular parabolic with Levi
$P'$ to be the block upper triangular parabolic with Levi ![]() $M'=w_0Mw_0^{-1}$, where
$M'=w_0Mw_0^{-1}$, where ![]() $w_0\in W$ is the longest element. Write
$w_0\in W$ is the longest element. Write ![]() $\check M'=\operatorname {GL}_{r_s}\times \cdots \times \operatorname {GL}_{r_1}$ and consider the morphisms
$\check M'=\operatorname {GL}_{r_s}\times \cdots \times \operatorname {GL}_{r_1}$ and consider the morphisms
 \[ \begin{aligned} \alpha:{X}_{\check P'} & \longrightarrow X_{\check M'},\\ \beta:\tilde{X}_{\check P'} & \longrightarrow X_{\check G}. \end{aligned} \]
\[ \begin{aligned} \alpha:{X}_{\check P'} & \longrightarrow X_{\check M'},\\ \beta:\tilde{X}_{\check P'} & \longrightarrow X_{\check G}. \end{aligned} \]
The choice of ![]() $\check M'\hookrightarrow \check P'$ defines an embedding
$\check M'\hookrightarrow \check P'$ defines an embedding ![]() $\iota :X_{\check M'}\hookrightarrow X_{\check P'}$. We will write
$\iota :X_{\check M'}\hookrightarrow X_{\check P'}$. We will write ![]() $(x_s,\ldots,x_1)\in X_{\check M'}$ for the point defined by
$(x_s,\ldots,x_1)\in X_{\check M'}$ for the point defined by
and write ![]() $Z_{\check M'}(x_1,\ldots,x_s)$ for the Zariski closure of its
$Z_{\check M'}(x_1,\ldots,x_s)$ for the Zariski closure of its ![]() $\check M'$-orbit
$\check M'$-orbit ![]() $\check M'\cdot (x_s,\ldots,x_1)$. Then one easily checks that the choice of ordering of
$\check M'\cdot (x_s,\ldots,x_1)$. Then one easily checks that the choice of ordering of ![]() $\lambda _1,\ldots,\lambda _s$ implies that
$\lambda _1,\ldots,\lambda _s$ implies that
is the Zariski closure of the ![]() $\check P'$-orbit of
$\check P'$-orbit of ![]() $\iota (x_s,\ldots, x_1)$. Moreover, the choice of ordering implies that
$\iota (x_s,\ldots, x_1)$. Moreover, the choice of ordering implies that ![]() $\alpha$ is smooth along this pre-image. In particular,
$\alpha$ is smooth along this pre-image. In particular,
Let ![]() $Z_{\check G}(x_s,\ldots,x_1)\subset \tilde X_{\check P'}$ denote the
$Z_{\check G}(x_s,\ldots,x_1)\subset \tilde X_{\check P'}$ denote the ![]() $\check G$-invariant closed subscheme of
$\check G$-invariant closed subscheme of ![]() $\tilde X_{\check P'}$ corresponding to the
$\tilde X_{\check P'}$ corresponding to the ![]() $\check P'$-invariant closed subscheme
$\check P'$-invariant closed subscheme ![]() $Z_{\check P'}(x_s,\ldots,x_1)\subset X_{\check P'}$. Using Corollary 4.42 and compatibility of
$Z_{\check P'}(x_s,\ldots,x_1)\subset X_{\check P'}$. Using Corollary 4.42 and compatibility of ![]() $R_G$ with parabolic induction, we are left to show that
$R_G$ with parabolic induction, we are left to show that
This follows, as the construction implies that ![]() $\beta$ maps
$\beta$ maps ![]() $Z_{\check G}(x_s,\ldots,x_1)$ isomorphically onto the Zariski closure
$Z_{\check G}(x_s,\ldots,x_1)$ isomorphically onto the Zariski closure ![]() $X_{\check G,[\varphi,N]}$ of the
$X_{\check G,[\varphi,N]}$ of the ![]() $\check G$-orbit
$\check G$-orbit ![]() $\check G\cdot (\varphi,N)=\check G\cdot \iota (x_s\ldots,x_1)$.
$\check G\cdot (\varphi,N)=\check G\cdot \iota (x_s\ldots,x_1)$.
We also remark that Theorem 4.38 is true for all regular semi-simple elements ![]() $\varphi$.
$\varphi$.
Corollary 4.44 Let ![]() $\varphi \in \check T(C)$ be regular semi-simple and
$\varphi \in \check T(C)$ be regular semi-simple and ![]() $\chi :\mathfrak {Z}\rightarrow C$ the character defined by the image of
$\chi :\mathfrak {Z}\rightarrow C$ the character defined by the image of ![]() $\varphi$ in
$\varphi$ in ![]() $\check T/W$. The set of functors
$\check T/W$. The set of functors
for standard Levi subgroups ![]() $M\subset G$, is uniquely determined (up to isomorphism) by requiring that they are
$M\subset G$, is uniquely determined (up to isomorphism) by requiring that they are ![]() $\hat {\mathfrak {Z}}_{M,\chi }$-linear, compatible with parabolic induction, and that
$\hat {\mathfrak {Z}}_{M,\chi }$-linear, compatible with parabolic induction, and that ![]() $\hat R_{T,\chi }$ is induced by the identification
$\hat R_{T,\chi }$ is induced by the identification
Proof. As in the proof of Theorem 4.38 the images of ![]() $\hat R_{G,\chi }(\hat \delta _w)$ are uniquely determined up to isomorphism and it is enough to prove that the same is true for the images of intertwining operators. Without loss of generality we may assume
$\hat R_{G,\chi }(\hat \delta _w)$ are uniquely determined up to isomorphism and it is enough to prove that the same is true for the images of intertwining operators. Without loss of generality we may assume
with ![]() $q^{-a}\lambda _i\neq q^{-b}\lambda _j$ for
$q^{-a}\lambda _i\neq q^{-b}\lambda _j$ for ![]() $i\neq j, a=0,\ldots,r_i-1,\ b=0,\ldots, r_j-1$, and
$i\neq j, a=0,\ldots,r_i-1,\ b=0,\ldots, r_j-1$, and ![]() $\lambda _i\neq q^{-r_j}\lambda _j$. Let
$\lambda _i\neq q^{-r_j}\lambda _j$. Let ![]() $M={\rm GL}_{r_1}(F)\times \cdots \times {\rm GL}_{r_s}(F)$ be the block diagonal Levi subgroup with block sizes
$M={\rm GL}_{r_1}(F)\times \cdots \times {\rm GL}_{r_s}(F)$ be the block diagonal Levi subgroup with block sizes ![]() $(r_1,\ldots, r_s)$ and
$(r_1,\ldots, r_s)$ and ![]() $P$ the corresponding block upper triangular parabolic subgroup.
$P$ the corresponding block upper triangular parabolic subgroup.
Further, let ![]() $\varphi _i={\rm diag}(\lambda _i,q^{-1}\lambda _i,\ldots,q^{-(r_i-1)}\lambda _i)\in {\rm GL}_{r_i}(F)$. For
$\varphi _i={\rm diag}(\lambda _i,q^{-1}\lambda _i,\ldots,q^{-(r_i-1)}\lambda _i)\in {\rm GL}_{r_i}(F)$. For ![]() $w_i\in \mathcal {S}_{r_i}$ we write
$w_i\in \mathcal {S}_{r_i}$ we write ![]() $\hat \delta ^{(i)}_{w_i}$ for the universal unramified deformation of the character defined by
$\hat \delta ^{(i)}_{w_i}$ for the universal unramified deformation of the character defined by ![]() $w_i\varphi _i$. Then, by means of an intertwining operator, every
$w_i\varphi _i$. Then, by means of an intertwining operator, every ![]() $\iota _{\overline {B}}^G\hat \delta _w$ is isomorphic to
$\iota _{\overline {B}}^G\hat \delta _w$ is isomorphic to
for some ![]() $(w_1,\ldots,w_s)\in \mathcal {S}_{r_1}\times \cdots \times \mathcal {S}_{r_s}=W_M$. As in the proof of Theorem 4.38 we deduce that, given two functors
$(w_1,\ldots,w_s)\in \mathcal {S}_{r_1}\times \cdots \times \mathcal {S}_{r_s}=W_M$. As in the proof of Theorem 4.38 we deduce that, given two functors ![]() $\hat R_{G,\chi }$ and
$\hat R_{G,\chi }$ and ![]() $\hat R'_{G,\chi }$ satisfying the assumptions, it is enough to show that for all
$\hat R'_{G,\chi }$ satisfying the assumptions, it is enough to show that for all ![]() $w\in W_M$ there are isomorphisms
$w\in W_M$ there are isomorphisms
such that the diagrams

commute for all ![]() $w,w'\in W_M$. This follows from the statement of Theorem 4.38 and transitivity of intertwining operators under parabolic induction.
$w,w'\in W_M$. This follows from the statement of Theorem 4.38 and transitivity of intertwining operators under parabolic induction.
We finish by giving more details on the behavior of ![]() $R_G(\operatorname {c-ind}_K^G\sigma _\mathcal {P})$ in the three-dimensional case.
$R_G(\operatorname {c-ind}_K^G\sigma _\mathcal {P})$ in the three-dimensional case.
Example 4.45 In the case ![]() $n=3$ there are three partitions
$n=3$ there are three partitions ![]() $\mathcal {P}_{\rm min},\mathcal {P}_0,\mathcal {P}_{\rm max}$ of
$\mathcal {P}_{\rm min},\mathcal {P}_0,\mathcal {P}_{\rm max}$ of ![]() $n=3$. We have
$n=3$. We have
where the multiplicities are defined as in (4.4).
The sheaves ![]() $R_G((\operatorname {c-ind}_K^G\sigma _{\rm min})^I)$ and
$R_G((\operatorname {c-ind}_K^G\sigma _{\rm min})^I)$ and ![]() $R_G((\operatorname {c-ind}_K^G\sigma _{\rm max})^I)$ are determined in Proposition 4.27. Let us give a closer description of
$R_G((\operatorname {c-ind}_K^G\sigma _{\rm max})^I)$ are determined in Proposition 4.27. Let us give a closer description of
As discussed in Remark 4.28, the generic rank of ![]() $\mathcal {F}$ on
$\mathcal {F}$ on ![]() $Z_{\check G,\mathcal {P}'}$ is zero if
$Z_{\check G,\mathcal {P}'}$ is zero if ![]() $\mathcal {P}'=\mathcal {P}_{\rm min}$, one if
$\mathcal {P}'=\mathcal {P}_{\rm min}$, one if ![]() $\mathcal {P}'=\mathcal {P}_0$, and two if
$\mathcal {P}'=\mathcal {P}_0$, and two if ![]() $\mathcal {P}'=\mathcal {P}_{\rm max}$.
$\mathcal {P}'=\mathcal {P}_{\rm max}$.
We describe the completed stalks ![]() $\hat {\mathcal {F}}_x$ as modules over the complete local rings
$\hat {\mathcal {F}}_x$ as modules over the complete local rings ![]() $\hat {\mathcal {O}}_{X_{\check G},x}$ for
$\hat {\mathcal {O}}_{X_{\check G},x}$ for ![]() $C$-valued points
$C$-valued points ![]() $x=(\varphi,N)\in X_{\check G}$. To simplify the exposition we restrict ourselves to regular semi-simple
$x=(\varphi,N)\in X_{\check G}$. To simplify the exposition we restrict ourselves to regular semi-simple ![]() $\varphi$. Recall that
$\varphi$. Recall that ![]() $X_{\check G,\mathcal {P}_0}=Z_{\check G,\mathcal {P}_0}\cup Z_{\check G,\mathcal {P}_{\rm max}}$ is a union of two irreducible components in this case. Moreover, recall that we write
$X_{\check G,\mathcal {P}_0}=Z_{\check G,\mathcal {P}_0}\cup Z_{\check G,\mathcal {P}_{\rm max}}$ is a union of two irreducible components in this case. Moreover, recall that we write ![]() $X_{\check G,0}=Z_{\check G,\mathcal {P}_{\rm max}}$ for the irreducible component defined by
$X_{\check G,0}=Z_{\check G,\mathcal {P}_{\rm max}}$ for the irreducible component defined by ![]() $N=0$.
$N=0$.
(a) Assume ![]() $x\in Z_{\check G,\mathcal {P}_{\rm min}}\backslash X_{\check G,\mathcal {P}_0}$. Then
$x\in Z_{\check G,\mathcal {P}_{\rm min}}\backslash X_{\check G,\mathcal {P}_0}$. Then ![]() $\hat {\mathcal {F}}_x=0$.
$\hat {\mathcal {F}}_x=0$.
(b) Assume ![]() $x\in Z_{\check G,\mathcal {P}_0}\backslash Z_{\check G,\mathcal {P}_{\rm max}}$. Then
$x\in Z_{\check G,\mathcal {P}_0}\backslash Z_{\check G,\mathcal {P}_{\rm max}}$. Then ![]() $\hat {\mathcal {F}}_x\cong \hat {\mathcal {O}}_{X_{\check G},x}$.
$\hat {\mathcal {F}}_x\cong \hat {\mathcal {O}}_{X_{\check G},x}$.
(c) Assume ![]() $x\in Z_{\check G,\mathcal {P}_{\rm max}}\backslash Z_{\check G,\mathcal {P}_0}$. Then
$x\in Z_{\check G,\mathcal {P}_{\rm max}}\backslash Z_{\check G,\mathcal {P}_0}$. Then ![]() $\hat {\mathcal {F}}_x\cong \hat {\mathcal {O}}_{X_{\check G},x}^2$.
$\hat {\mathcal {F}}_x\cong \hat {\mathcal {O}}_{X_{\check G},x}^2$.
(d) Assume ![]() $x\in Z_{\check G,\mathcal {P}_{\rm max}}\cap Z_{\check G,\mathcal {P}_0}$. Without loss of generality we may assume
$x\in Z_{\check G,\mathcal {P}_{\rm max}}\cap Z_{\check G,\mathcal {P}_0}$. Without loss of generality we may assume ![]() $\varphi ={\rm diag}(\lambda _1,\lambda _2,\lambda _3)$. As before, we write
$\varphi ={\rm diag}(\lambda _1,\lambda _2,\lambda _3)$. As before, we write ![]() $\chi :\mathfrak {Z}\rightarrow C$ for the character defined by the characteristic polynomial of
$\chi :\mathfrak {Z}\rightarrow C$ for the character defined by the characteristic polynomial of ![]() $\varphi$. Up to renumbering, we have to distinguish two cases.
$\varphi$. Up to renumbering, we have to distinguish two cases.
(d1) ![]() $\lambda _2=q^{-1}\lambda _1$ and
$\lambda _2=q^{-1}\lambda _1$ and ![]() $\lambda _3\notin \{q^{-1}\lambda _2,q\lambda _1\}$. In this case
$\lambda _3\notin \{q^{-1}\lambda _2,q\lambda _1\}$. In this case ![]() $Z_{\check G,\mathcal {P}_0}$ and
$Z_{\check G,\mathcal {P}_0}$ and ![]() $Z_{\check G,\mathcal {P}_{\rm max}}$ are smooth at
$Z_{\check G,\mathcal {P}_{\rm max}}$ are smooth at ![]() $x$. Moreover (using the notation introduced above),
$x$. Moreover (using the notation introduced above),
for some ![]() $w_1,w_2\in W$ and (with appropriate numeration)
$w_1,w_2\in W$ and (with appropriate numeration)
We then can use compatibility of ![]() $R_G$ with parabolic induction to deduce that
$R_G$ with parabolic induction to deduce that
(d2) ![]() $\lambda _3=q^{-1}\lambda _2=q^{-2}\lambda _1$. In this case
$\lambda _3=q^{-1}\lambda _2=q^{-2}\lambda _1$. In this case ![]() $Z_{\check G,\mathcal {P}_0}$ is no longer smooth at
$Z_{\check G,\mathcal {P}_0}$ is no longer smooth at ![]() $x$, but has a self-intersection as can be seen from the description of the complete local ring: using a local presentation as in (4.25), we can compute that the complete local ring of
$x$, but has a self-intersection as can be seen from the description of the complete local ring: using a local presentation as in (4.25), we can compute that the complete local ring of ![]() $\hat {\mathcal {O}}_{X_{\check G},x}$ is smoothly equivalent to
$\hat {\mathcal {O}}_{X_{\check G},x}$ is smoothly equivalent to
With these coordinates the completion of ![]() $Z_{\check G,\mathcal {P}_{\rm min}}$ at
$Z_{\check G,\mathcal {P}_{\rm min}}$ at ![]() $x$ is given by the vanishing locus
$x$ is given by the vanishing locus ![]() $V(t_1-t_2,t_2-t_3)$, and the completion of
$V(t_1-t_2,t_2-t_3)$, and the completion of ![]() $Z_{\check G,{\mathcal {P}_{\rm max}}}$ is given by
$Z_{\check G,{\mathcal {P}_{\rm max}}}$ is given by ![]() $V(u_1,u_2)$. Moreover, both are smooth at
$V(u_1,u_2)$. Moreover, both are smooth at ![]() $x$. However, the completion of
$x$. However, the completion of ![]() $Z_{\check G,\mathcal {P}_0}$ is given by
$Z_{\check G,\mathcal {P}_0}$ is given by ![]() $V(t_1-t_2,u_2)\cup V(u_1,t_2-t_3)$, that is, it decomposes into two components, say
$V(t_1-t_2,u_2)\cup V(u_1,t_2-t_3)$, that is, it decomposes into two components, say ![]() $\hat {Z}_1$ and
$\hat {Z}_1$ and ![]() $\hat {Z}_2$. Note that this computation implies that
$\hat {Z}_2$. Note that this computation implies that ![]() $Z_{\check G,\mathcal {P}_0}$ cannot be Cohen–Macaulay at
$Z_{\check G,\mathcal {P}_0}$ cannot be Cohen–Macaulay at ![]() $x$, as it has a self-intersection in codimension two. We can compute the completions of the compactly induced representation:
$x$, as it has a self-intersection in codimension two. We can compute the completions of the compactly induced representation:
 \begin{align*} \operatorname{c-ind}_K^G\sigma_{\mathcal{P}_{\rm max}}\otimes_{\mathfrak{Z}}\hat{\mathfrak{Z}}_\chi&\cong \iota_{\overline{B}}^G \hat\delta_{1},\\ \operatorname{c-ind}_K^G\sigma_{\mathcal{P}_0}\otimes_{\mathfrak{Z}}\hat{\mathfrak{Z}}_\chi&\cong \iota_{\overline{B}}^G \hat\delta_{w_1}\oplus \iota_{\overline{B}}^G \hat\delta_{w_2},\\ \operatorname{c-ind}_K^G\sigma_{\mathcal{P}_{\rm min}}\otimes_{\mathfrak{Z}}\hat{\mathfrak{Z}}_\chi&\cong \iota_{\overline{B}}^G \hat\delta_{w_0}, \end{align*}
\begin{align*} \operatorname{c-ind}_K^G\sigma_{\mathcal{P}_{\rm max}}\otimes_{\mathfrak{Z}}\hat{\mathfrak{Z}}_\chi&\cong \iota_{\overline{B}}^G \hat\delta_{1},\\ \operatorname{c-ind}_K^G\sigma_{\mathcal{P}_0}\otimes_{\mathfrak{Z}}\hat{\mathfrak{Z}}_\chi&\cong \iota_{\overline{B}}^G \hat\delta_{w_1}\oplus \iota_{\overline{B}}^G \hat\delta_{w_2},\\ \operatorname{c-ind}_K^G\sigma_{\mathcal{P}_{\rm min}}\otimes_{\mathfrak{Z}}\hat{\mathfrak{Z}}_\chi&\cong \iota_{\overline{B}}^G \hat\delta_{w_0}, \end{align*}
where ![]() $w_0\in W$ is the longest element and
$w_0\in W$ is the longest element and ![]() $w_1,w_2\in W\backslash \{1,w_0\}$. Here the elements
$w_1,w_2\in W\backslash \{1,w_0\}$. Here the elements ![]() $w_1,w_2$ are chosen such that
$w_1,w_2$ are chosen such that
is the set (consisting of four pairwise non-isomorphic elements) of induced representations of the form ![]() $\iota _{\overline {B}}^G \hat \delta _{w}$. Using compatibility with parabolic induction, we deduce that (in the coordinates introduced above)
$\iota _{\overline {B}}^G \hat \delta _{w}$. Using compatibility with parabolic induction, we deduce that (in the coordinates introduced above)
 \begin{align*} \hat{\mathcal{F}}_x&=C[\![t_1,t_2,t_3,u_1,u_2]\!]/((t_1-t_2)u_1,u_2)\\ &\quad \oplus C[\![t_1,t_2,t_3,u_1,u_2]\!]/(u_1,(t_2-t_3)u_2). \end{align*}
\begin{align*} \hat{\mathcal{F}}_x&=C[\![t_1,t_2,t_3,u_1,u_2]\!]/((t_1-t_2)u_1,u_2)\\ &\quad \oplus C[\![t_1,t_2,t_3,u_1,u_2]\!]/(u_1,(t_2-t_3)u_2). \end{align*}
In other words, the completion ![]() $\hat {\mathcal {F}}_x$ is the direct sum of the structure sheaves of
$\hat {\mathcal {F}}_x$ is the direct sum of the structure sheaves of ![]() $\hat X_{\check G,0,x}\cup \hat Z_1$ and
$\hat X_{\check G,0,x}\cup \hat Z_1$ and ![]() $\hat X_{\check G,0,x}\cup \hat Z_2$.
$\hat X_{\check G,0,x}\cup \hat Z_2$.
Acknowledgements
I would very much like to thank Christophe Breuil, Michael Rapoport, Timo Richarz, Peter Schneider, Jakob Scholbach, Benjamin Schraen and Matthias Strauch for many helpful discussions and for their interest. Moreover, I would like to thank Johannes Anschütz and Arthur-César Le-Bras for asking many helpful questions and pointing out some mistakes in an earlier version of the paper. Special thanks go to Peter Scholze for his constant interest and encouragement after I explained my first computations to him. I finally would like to thank the referee for his/her careful reading and comments.