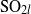Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Soudry, David
and
Tanay, Yaacov
2015.
On local descent for unitary groups.
Journal of Number Theory,
Vol. 146,
Issue. ,
p.
557.
Kaplan, Eyal
2015.
Complementary results on the Rankin–Selberg gamma factors of classical groups.
Journal of Number Theory,
Vol. 146,
Issue. ,
p.
390.
Cai, Yuanqing
Friedberg, Solomon
Ginzburg, David
and
Kaplan, Eyal
2019.
Doubling constructions and tensor product L-functions: the linear case.
Inventiones mathematicae,
Vol. 217,
Issue. 3,
p.
985.
Jo, Yeongseong
2020.
Rankin–Selberg L-functions via good sections.
Forum Mathematicum,
Vol. 32,
Issue. 4,
p.
1039.
Jo, Yeongseong
2021.
RANKIN–SELBERG INTEGRALS FOR LOCAL SYMMETRIC SQUARE FACTORS ON GL(2).
Mathematika,
Vol. 67,
Issue. 2,
p.
388.
Cheng, Yao
2022.
Rankin–Selberg integrals for $$\mathrm{SO}_{2n+1}{\times }\mathrm{GL}_r$$ attached to newforms and oldforms.
Mathematische Zeitschrift,
Vol. 301,
Issue. 4,
p.
3973.
Cai, Yuanqing
Friedberg, Solomon
and
Kaplan, Eyal
2022.
The generalized doubling method: local theory.
Geometric and Functional Analysis,
Vol. 32,
Issue. 6,
p.
1233.
Kaplan, Eyal
Lau, Jing Feng
and
Liu, Baiying
2023.
Local descent to quasi-split even general spin groups.
Mathematische Zeitschrift,
Vol. 303,
Issue. 3,
Cheng, Yao
2024.
On the Rankin–Selberg L-factors for SO5 × GL2.
Israel Journal of Mathematics,
Vol. 261,
Issue. 1,
p.
313.
Luo, Caihua
2024.
Holomorphy of normalized intertwining operators for certain induced representations.
Mathematische Annalen,
Vol. 389,
Issue. 4,
p.
4019.
Adrian, Moshe
Henniart, Guy
Kaplan, Eyal
and
Oi, Masao
2025.
Simple supercuspidal L$L$‐packets of split special orthogonal groups over dyadic fields.
Journal of the London Mathematical Society,
Vol. 112,
Issue. 1,
Hazeltine, Alexander
and
Liu, Baiying
2025.
On the local converse theorem for split 𝑆𝑂_{2𝑙}.
Representation Theory,
Vol. 29,
Issue. 7,
p.
209.