Article contents
On the metric theory of approximations by reduced fractions: a quantitative Koukoulopoulos–Maynard theorem
Published online by Cambridge University Press: 03 February 2023
Abstract
Let 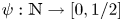 $\psi : \mathbb {N} \to [0,1/2]$ be given. The Duffin–Schaeffer conjecture, recently resolved by Koukoulopoulos and Maynard, asserts that for almost all reals
$\psi : \mathbb {N} \to [0,1/2]$ be given. The Duffin–Schaeffer conjecture, recently resolved by Koukoulopoulos and Maynard, asserts that for almost all reals 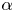 $\alpha$ there are infinitely many coprime solutions
$\alpha$ there are infinitely many coprime solutions 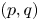 $(p,q)$ to the inequality
$(p,q)$ to the inequality 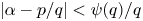 $|\alpha - p/q| < \psi (q)/q$, provided that the series
$|\alpha - p/q| < \psi (q)/q$, provided that the series 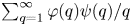 $\sum _{q=1}^\infty \varphi (q) \psi (q) / q$ is divergent. In the present paper, we establish a quantitative version of this result, by showing that for almost all
$\sum _{q=1}^\infty \varphi (q) \psi (q) / q$ is divergent. In the present paper, we establish a quantitative version of this result, by showing that for almost all 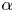 $\alpha$ the number of coprime solutions
$\alpha$ the number of coprime solutions 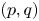 $(p,q)$, subject to
$(p,q)$, subject to 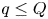 $q \leq Q$, is of asymptotic order
$q \leq Q$, is of asymptotic order 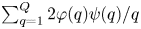 $\sum _{q=1}^Q 2 \varphi (q) \psi (q) / q$. The proof relies on the method of GCD graphs as invented by Koukoulopoulos and Maynard, together with a refined overlap estimate from sieve theory, and number-theoretic input on the ‘anatomy of integers’. The key phenomenon is that the system of approximation sets exhibits ‘asymptotic independence on average’ as the total mass of the set system increases.
$\sum _{q=1}^Q 2 \varphi (q) \psi (q) / q$. The proof relies on the method of GCD graphs as invented by Koukoulopoulos and Maynard, together with a refined overlap estimate from sieve theory, and number-theoretic input on the ‘anatomy of integers’. The key phenomenon is that the system of approximation sets exhibits ‘asymptotic independence on average’ as the total mass of the set system increases.
Keywords
Information
- Type
- Research Article
- Information
- Copyright
- © 2023 The Author(s). The publishing rights in this article are licensed to Foundation Compositio Mathematica under an exclusive licence
References
- 3
- Cited by


