Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Paškūnas, Vytautas
2010.
Admissible unitary completions of locally ℚ_{𝕡}-rational representations of 𝔾𝕃₂(𝔽).
Representation Theory of the American Mathematical Society,
Vol. 14,
Issue. 9,
p.
324.
Berger, Laurent
2010.
On some modular representations of the Borel subgroup of GL2(Qp).
Compositio Mathematica,
Vol. 146,
Issue. 1,
p.
58.
Hu, Yongquan
2012.
Diagrammes canoniques et représentations modulo p de GL2(F).
Journal of the Institute of Mathematics of Jussieu,
Vol. 11,
Issue. 1,
p.
67.
Chojecki, Przemysław
2015.
On non-abelian Lubin–Tate theory for .
Compositio Mathematica,
Vol. 151,
Issue. 8,
p.
1433.
Hu, Yongquan
2017.
An application of a theorem of Emerton to mod p representations of GL 2.
Journal of the London Mathematical Society,
Vol. 96,
Issue. 3,
p.
545.
Herzig, Florian
Le, Daniel
and
Morra, Stefano
2017.
On mod local-global compatibility for in the ordinary case.
Compositio Mathematica,
Vol. 153,
Issue. 11,
p.
2215.
Xu, Peng
2025.
Restriction of p-modular representations of U(2,1) to a Borel subgroup.
International Journal of Number Theory,
Vol. 21,
Issue. 06,
p.
1229.

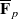 -vector spaces to
-vector spaces to 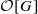 -modules of finite length and unitary
-modules of finite length and unitary 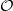 is the ring of integers of a complete discretely valued field
is the ring of integers of a complete discretely valued field 