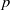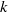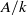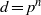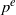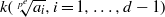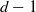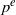Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Chapman, Adam
2017.
Symbol length of p-algebras of prime exponent.
Journal of Algebra and Its Applications,
Vol. 16,
Issue. 07,
p.
1750136.
Pumplün, S.
2018.
Algebras whose right nucleus is a central simple algebra.
Journal of Pure and Applied Algebra,
Vol. 222,
Issue. 9,
p.
2773.
Chapman, Adam
and
McKinnie, Kelly
2020.
Essential Dimension, Symbol Length and -rank.
Canadian Mathematical Bulletin,
Vol. 63,
Issue. 4,
p.
882.
Becher, Karim Johannes
Bi̇ngöl, Fatma Kader
and
Leep, David B.
2022.
Splitting quaternion algebras defined over a finite field extension.
Journal of Algebra and Its Applications,
Vol. 21,
Issue. 03,
Bingöl, Fatma Kader
2024.
Symbol length in positive characteristic.
Journal of Pure and Applied Algebra,
Vol. 228,
Issue. 6,
p.
107613.