Article contents
On the u∞-torsion submodule of prismatic cohomology
Published online by Cambridge University Press: 30 June 2023
Abstract
We investigate the maximal finite length submodule of the Breuil–Kisin prismatic cohomology of a smooth proper formal scheme over a 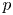 $p$-adic ring of integers. This submodule governs pathology phenomena in integral
$p$-adic ring of integers. This submodule governs pathology phenomena in integral 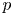 $p$-adic cohomology theories. Geometric applications include a control, in low degrees and mild ramifications, of (1) the discrepancy between two naturally associated Albanese varieties in characteristic
$p$-adic cohomology theories. Geometric applications include a control, in low degrees and mild ramifications, of (1) the discrepancy between two naturally associated Albanese varieties in characteristic 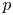 $p$, and (2) the kernel of the specialization map in
$p$, and (2) the kernel of the specialization map in 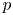 $p$-adic étale cohomology. As an arithmetic application, we study the boundary case of the theory due to Fontaine and Laffaille, Fontaine and Messing, and Kato. Also included is an interesting example, generalized from a construction in Bhatt, Morrow and Scholze's work, which illustrates some of our theoretical results being sharp, and negates a question of Breuil.
$p$-adic étale cohomology. As an arithmetic application, we study the boundary case of the theory due to Fontaine and Laffaille, Fontaine and Messing, and Kato. Also included is an interesting example, generalized from a construction in Bhatt, Morrow and Scholze's work, which illustrates some of our theoretical results being sharp, and negates a question of Breuil.
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- © 2023 The Author(s). The publishing rights in this article are licensed to Foundation Compositio Mathematica under an exclusive licence
References
- 1
- Cited by


