Article contents
On two arithmetic theta lifts
Published online by Cambridge University Press: 07 September 2018
Abstract
Our aim is to clarify the relationship between Kudla’s and Bruinier’s Green functions attached to special cycles on Shimura varieties of orthogonal and unitary type, which play a key role in the arithmetic geometry of these cycles in the context of Kudla’s program. In particular, we show that the generating series obtained by taking the differences of the two families of Green functions is a non-holomorphic modular form and has trivial (cuspidal) holomorphic projection. Along the way, we construct a section of the Maaß lowering operator for moderate growth forms valued in the Weil representation using a regularized theta lift, which may be of independent interest, as it in particular has applications to mock modular forms. We also consider arithmetic-geometric applications to integral models of 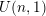 $U(n,1)$ Shimura varieties. Each family of Green functions gives rise to a formal arithmetic theta function, valued in an arithmetic Chow group, that is conjectured to be modular; our main result is the modularity of the difference of the two arithmetic theta functions. Finally, we relate the arithmetic heights of the special cycles to special derivatives of Eisenstein series, as predicted by Kudla’s conjecture, and describe a refinement of a theorem of Bruinier, Howard and Yang on arithmetic intersections against CM points.
$U(n,1)$ Shimura varieties. Each family of Green functions gives rise to a formal arithmetic theta function, valued in an arithmetic Chow group, that is conjectured to be modular; our main result is the modularity of the difference of the two arithmetic theta functions. Finally, we relate the arithmetic heights of the special cycles to special derivatives of Eisenstein series, as predicted by Kudla’s conjecture, and describe a refinement of a theorem of Bruinier, Howard and Yang on arithmetic intersections against CM points.
Information
- Type
- Research Article
- Information
- Copyright
- © The Authors 2018
References
- 6
- Cited by

