Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-26T09:12:21.923Z Has data issue: false hasContentIssue false
  • English
  • Français

On uniqueness of p-adic period morphisms, II

Published online by Cambridge University Press:  10 November 2020

Wiesława Nizioł
Wiesława Nizioł*
Affiliation:
CNRS, IMJ-PRG, Sorbonne Université, 4 place Jussieu, 75005Paris, Francewieslawa.niziol@imj-prg.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove equality of the various rational 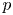$p$-adic period morphisms for smooth, not necessarily proper, schemes. We start with showing that the 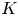$K$-theoretical uniqueness criterion we had found earlier for proper smooth schemes extends to proper finite simplicial schemes in the good reduction case and to cohomology with compact support in the semistable reduction case. It yields the equality of the period morphisms for cohomology with compact support defined using the syntomic, almost étale, and motivic constructions. We continue with showing that the 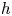$h$-cohomology period morphism agrees with the syntomic and almost étale period morphisms whenever the latter morphisms are defined (and up to a change of Hyodo–Kato cohomology). We do it by lifting the syntomic and almost étale period morphisms to the 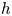$h$-site of varieties over a field, where their equality with the 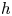$h$-cohomology period morphism can be checked directly using the Beilinson Poincaré lemma and the case of dimension 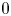$0$. This also shows that the syntomic and almost étale period morphisms have a natural extension to the Voevodsky triangulated category of motives and enjoy many useful properties (since so does the 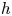$h$-cohomology period morphism).

Keywords

p-adic period morphismsK-theorymotives
Type
Research Article
Information
Compositio Mathematica , Volume 156 , Issue 9 , September 2020 , pp. 1915 - 1964
Check for updates
Copyright
Copyright © The Author(s) 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This research was supported in part by the NSF grant DMS0703696 and the grant ANR-14-CE25.

References

Abbes, A. and Gros, M., Covanishing topos and generalizations, in The p-adic Simpson correspondence, Annals of Mathematics Studies, vol. 193 (Princeton University Press, Princeton, NJ, 2016), 485–576.10.1515/9781400881239-007CrossRefGoogle Scholar
Achinger, P., $K(\pi ,1)$-neighborhoods and comparison theorems, Compos. Math. 151 (2015), 1945–1964.10.1112/S0010437X15007319CrossRefGoogle Scholar
Akhtar, R., A mod-l vanishing theorem of Beilinson–Soulé type, J. Pure Appl. Algebra 208 (2007), 555–560.10.1016/j.jpaa.2006.01.017CrossRefGoogle Scholar
Artin, M., Grothendieck, A. and Verdier, J. L., Théorie des topos et cohomologie étale des schémas. Tome 3. Séminaire de Géométrie Algébrique du Bois-Marie 1963–1964 (SGA 4), Lecture Notes in Mathematics, vol. 305 (Springer, Berlin–New York, 1973).Google Scholar
Beilinson, A., p-adic periods and derived de Rham cohomology, J. Amer. Math. Soc. 25 (2012), 715–738.10.1090/S0894-0347-2012-00729-2CrossRefGoogle Scholar
Beilinson, A., On the crystalline period map, Preprint (2013), arXiv:1111.3316v4. This is an extended version of Camb. J. Math. 1 (2013), 1–51.Google Scholar
Berthelot, P. and Ogus, A., F-isocrystals and de Rham cohomology. I, Invent. Math. 72 (1983), 159–199.10.1007/BF01389319CrossRefGoogle Scholar
Bhatt, B., p-adic derived de Rham cohomology, Preprint (2012), arXiv:1204.6560.Google Scholar
Bhatt, B., Morrow, M. and Scholze, P., Integral p-adic Hodge theory, Publ. Math. Inst. Hautes Études Sci. 128 (2018), 219–397.10.1007/s10240-019-00102-zCrossRefGoogle Scholar
Bhatt, B., Morrow, M. and Scholze, P., Topological Hochschild homology and integral p-adic Hodge theory, Publ. Math. Inst. Hautes Études Sci. 129 (2019), 199–310.10.1007/s10240-019-00106-9CrossRefGoogle Scholar
Bousfield, A. K. and Kan, D., Homotopy limits, completions and localizations, Lecture Notes in Mathematics, vol. 304 (Springer, Berlin–New York, 1972).10.1007/978-3-540-38117-4CrossRefGoogle Scholar
Česnavičius, K. and Koshikawa, T., The $\mathbf {A}_{\rm inf}$-cohomology in the semistable case, Compos. Math. 155 (2019), 2039–2128.10.1112/S0010437X1800790XCrossRefGoogle Scholar
Cisinski, D.-C. and Déglise, F., Integral mixed motives in equal characteristic, Doc. Math. Extra Vol. Merkurjev (2015), 145–194.Google Scholar
Cisinski, D.-C. and Déglise, F., Triangulated categories of mixed motives, Springer Monographs in Mathematics (Springer, 2019).10.1007/978-3-030-33242-6CrossRefGoogle Scholar
Colmez, P., Espaces de Banach de dimension finite, J. Inst. Math. Jussieu 1 (2002), 331–439.10.1017/S1474748002000099CrossRefGoogle Scholar
Colmez, P., Dospinescu, G. and Nizioł, W., Integral p-adic étale cohomology of Drinfeld symmetric spaces, Preprint (2019), arXiv:1905.11495.Google Scholar
Colmez, P., Dospinescu, G. and Nizioł, W., Cohomology of p-adic Stein spaces, Invent. Math. 219 (2020), 873–985.10.1007/s00222-019-00923-zCrossRefGoogle Scholar
Colmez, P. and Nizioł, W., Syntomic complexes and p-adic nearby cycles, Invent. Math. 208 (2017), 1–108.10.1007/s00222-016-0683-3CrossRefGoogle Scholar
Deligne, P., Théorie de Hodge. III, Publ. Math. Inst. Hautes Études Sci. 44 (1974), 5–77.10.1007/BF02685881CrossRefGoogle Scholar
Deligne, P. and Illusie, L., Relévements modulo $p^2$ et décomposition du complexe de de Rham, Invent. Math. 89 (1987), 247–270.10.1007/BF01389078CrossRefGoogle Scholar
Déglise, F. and Nizioł, W., On p-adic absolute Hodge cohomology and syntomic coefficients, I, Comment. Math. Helv. 93 (2018), 71–131.10.4171/CMH/430CrossRefGoogle Scholar
Diao, H., Lan, K.-W., Liu, R. and Zhu, X., Logarithmic Riemann–Hilbert correspondences for rigid varieties, Preprint (2019), arXiv:1803.05786.Google Scholar
Faltings, G., p-adic Hodge-theory, J. Amer. Math. Soc. 1 (1988), 255–299.Google Scholar
Faltings, G., Crystalline cohomology and p-adic Galois representations, in Algebraic analysis, geometry and number theory, ed. Igusa, J. I. (Johns Hopkins University Press, Baltimore, MD, 1989), 25–80.Google Scholar
Faltings, G., Almost étale extensions, Cohomologies p-adiques et applications arithmétiques, II, Astérisque 279 (2002), 185–270.Google Scholar
Fontaine, J.-M., Le corps des périodes p-adiques, Astérisque 223 (1994), 59–111.Google Scholar
Fontaine, J.-M. and Lafaille, G., Construction de représentations p-adiques, Ann. Sci. Éc. Norm. Supér. (4) 15 (1982), 547–608.10.24033/asens.1437CrossRefGoogle Scholar
Fontaine, J.-M. and Messing, W., p-adic periods and p-adic étale cohomology, in Current trends in arithmetical algebraic geometry, ed. Ribet, K., Contemporary Mathematics, vol. 67 (American Mathematical Society, Providence, RI, 1987), 179–207.10.1090/conm/067/902593CrossRefGoogle Scholar
Geisser, T., Arithmetic homology and an integral version of Kato's conjecture, J. Reine Angew. Math. 644 (2010), 1–22.10.1515/crelle.2010.050CrossRefGoogle Scholar
Hyodo, O. and Kato, K., Semistable reduction and crystalline cohomology with logarithmic poles, Astérisque 223 (1994), 221–268.Google Scholar
Kato, K., Semistable reduction and p-adic étale cohomology, Astérisque 223 (1994), 269–293.Google Scholar
Kato, K., Toric singularities, Amer. J. Math. 116 (1994), 1073–1099.10.2307/2374941CrossRefGoogle Scholar
Kato, K. and Messing, W., Syntomic cohomology and p-adic étale cohomology, Tohoku Math. J. 44 (1992), 1–9.10.2748/tmj/1178227370CrossRefGoogle Scholar
Kisin, M., Potential semi-stability of p-adic étale cohomology, Israel J. Math. 129 (2002), 157–173.10.1007/BF02773161CrossRefGoogle Scholar
Levine, M., K-theory and motivic cohomology of schemes, Preprint (2004).Google Scholar
Li, Sh. and Pan, X., Logarithmic de Rham comparison for open rigid spaces, Forum Math. Sigma 7 (2019), e32.10.1017/fms.2019.27CrossRefGoogle Scholar
Nekovář, J. and Nizioł, W., Syntomic cohomology and p-adic regulators for varieties over p-adic fields, Algebra Number Theory 10 (2016), 1695–1790.10.2140/ant.2016.10.1695CrossRefGoogle Scholar
Nizioł, W., Crystalline conjecture via K-theory, Ann. Sci. Éc. Norm. Supér. (4) 31 (1998), 659–681.10.1016/S0012-9593(98)80003-7CrossRefGoogle Scholar
Nizioł, W., Toric singularities: log-blow-ups and global resolutions, J. Algebraic Geom. 15 (2006), 1–29.10.1090/S1056-3911-05-00409-1CrossRefGoogle Scholar
Nizioł, W., p-adic motivic cohomology and arithmetic, Proc. Int. Congr. Mathematicians, vol. II (European Mathematical Society, Zürich, 2006), 459–472.Google Scholar
Nizioł, W., Semistable conjecture via K-theory, Duke Math. J. 141 (2008), 151–178.10.1215/S0012-7094-08-14114-6CrossRefGoogle Scholar
Nizioł, W., On uniqueness of p-adic period morphisms, Pure Appl. Math. Q. 5 (2009), 163–212.Google Scholar
Nizioł, W., On syntomic regulators, I: constructions, Preprint (2016), arXiv:1607.04975.Google Scholar
Saito, T., Log smooth extension of a family of curves and semi-stable reduction, J. Algebraic Geom. 13 (2004), 287–321.CrossRefGoogle Scholar
Scholze, P., p-adic Hodge theory for rigid-analytic varieties, Forum Math. Pi 1 (2013), e1.10.1017/fmp.2013.1CrossRefGoogle Scholar
Soulé, C., Operations on étale K-theory. Applications, in Algebraic K-theory I, Lecture Notes in Mathematics, vol. 966 (Springer, Berlin–Heidelberg–New York, 1982), 271–303.10.1007/BFb0062180CrossRefGoogle Scholar
Suslin, A., Higher Chow groups and étale cohomology, in Cycles, transfers, and motivic homology theories, Annals of Mathematics Studies, vol. 143 (Princeton University Press, Princeton, NJ, 2000), 239– 254.Google Scholar
Tan, F. and Tong, J., Crystalline comparison isomorphisms in p-adic Hodge theory: the absolutely unramified case, Algebra Number Theory 13 (2019), 1509–1581.10.2140/ant.2019.13.1509CrossRefGoogle Scholar
Thomason, R., Algebraic K-theory and étale cohomology, Ann. Sci. Éc. Norm. Supér. (4) 18 (1985), 437–552.CrossRefGoogle Scholar
Tsuji, T., p-adic Hodge theory in the semi-stable reduction case, in Proc. Int. Congr. Mathematicians, vol. II (Berlin, 1998), Doc. Math. (1998), Extra Vol. II, 207–216 (electronic).Google Scholar
Tsuji, T., p-adic étale and crystalline cohomology in the semistable reduction case, Invent. Math. 137 (1999), 233–411.Google Scholar
Tsuji, T., Poincaré duality for logarithmic crystalline cohomology, Compos. Math. 118 (1999), 11–41.10.1023/A:1001020809306CrossRefGoogle Scholar
Tsuji, T., On the maximal unramified quotients of p-adic étale cohomology groups and logarithmic Hodge–Witt sheaves, Doc. Math. (2003), Extra Vol., 833–890.Google Scholar
Yamashita, G., p-adic Hodge theory for open varieties, C. R. Math. Acad. Sci. Paris 349 (2011), 1127–1130.10.1016/j.crma.2011.10.016CrossRefGoogle Scholar