Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-10T11:49:16.670Z Has data issue: false hasContentIssue false
  • English
  • Français

A 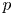$p$-adic monodromy theorem for de Rham local systems

Part of: Families, fibrations Arithmetic problems. Diophantine geometry Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  15 December 2022

Koji Shimizu
Koji Shimizu*
Affiliation:
Department of Mathematics, UC Berkeley, 943 Evans Hall, Berkeley, CA 94720-3840, USA shimizu@tsinghua.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

We study horizontal semistable and horizontal de Rham representations of the absolute Galois group of a certain smooth affinoid over a 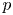$p$-adic field. In particular, we prove that a horizontal de Rham representation becomes horizontal semistable after a finite extension of the base field. As an application, we show that every de Rham local system on a smooth rigid analytic variety becomes horizontal semistable étale locally around every classical point. We also discuss potentially crystalline loci of de Rham local systems and cohomologically potentially good reduction loci of smooth proper morphisms.

Keywords

rigid analytic geometryp-adic Hodge theory

MSC classification

Primary: 14G22: Rigid analytic geometry
Secondary: 11F80: Galois representations 11F85: $p$-adic theory, local fields 14D10: Arithmetic ground fields (finite, local, global)
Type
Research Article
Information
Compositio Mathematica , Volume 158 , Issue 12 , December 2022 , pp. 2157 - 2205
Check for updates
Copyright
© 2022 The Author(s). The publishing rights in this article are licensed to Foundation Compositio Mathematica under an exclusive licence

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Current address: Yau Mathematical Sciences Center, Tsinghua University, W10 Ningzhai, Haidian, Beijing 100084, China

The author was supported by the National Science Foundation under Grant No. DMS-1638352 through membership of the Institute for Advanced Study.

References

Abramovich, D. and Karu, K., Weak semistable reduction in characteristic $0$, Invent. Math. 139 (2000), 241–273.CrossRefGoogle Scholar
Adiprasito, K., Liu, G. and Temkin, M., Semistable reduction in characteristic 0, Preprint (2018), arXiv:1810.03131v2.Google Scholar
Andreatta, F. and Iovita, A., Semistable sheaves and comparison isomorphisms in the semistable case, Rend. Semin. Mat. Univ. Padova 128 (2012), 131–285.CrossRefGoogle Scholar
Andreatta, F. and Iovita, A., Comparison isomorphisms for smooth formal schemes, J. Inst. Math. Jussieu 12 (2013), 77–151.CrossRefGoogle Scholar
Berger, L., Représentations $p$-adiques et équations différentielles, Invent. Math. 148 (2002), 219–284.CrossRefGoogle Scholar
Berger, L. and Colmez, P., Familles de représentations de de Rham et monodromie $p$-adique, Astérisque 319 (2008), 303–337, Représentations $p$-adiques de groupes $p$-adiques. I. Représentations galoisiennes et $(\phi, \Gamma )$-modules.Google Scholar
Berkovich, V. G., Spectral theory and analytic geometry over non-Archimedean fields, Mathematical Surveys and Monographs, vol. 33 (American Mathematical Society, Providence, RI, 1990).Google Scholar
Berkovich, V. G., Étale cohomology for non-Archimedean analytic spaces, Publ. Math. Inst. Hautes Études Sci. 78 (1993), 5–161 (1994).CrossRefGoogle Scholar
Berthelot, P. and Ogus, A., $F$-isocrystals and de Rham cohomology. I, Invent. Math. 72 (1983), 159–199.CrossRefGoogle Scholar
Bosch, S., Güntzer, U. and Remmert, R., A systematic approach to rigid analytic geometry, in Non-Archimedean analysis, Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], vol. 261 (Springer, Berlin, 1984).CrossRefGoogle Scholar
Brinon, O., Représentations cristallines dans le cas d'un corps résiduel imparfait, Ann. Inst. Fourier (Grenoble) 56 (2006), 919–999.CrossRefGoogle Scholar
Brinon, O., Représentations $p$-adiques cristallines et de de Rham dans le cas relatif, Mém. Soc. Math. Fr. (N.S.) 112 (2008.Google Scholar
Colmez, P., Espaces de Banach de dimension finie, J. Inst. Math. Jussieu 1 (2002), 331–439.CrossRefGoogle Scholar
Colmez, P. and Fontaine, J.-M., Construction des représentations $p$-adiques semi-stables, Invent. Math. 140 (2000), 1–43.CrossRefGoogle Scholar
de Jong, A. J., Smoothness, semi-stability and alterations, Publ. Math. Inst. Hautes Études Sci. 83 (1996), 51–93.CrossRefGoogle Scholar
Deligne, P., La conjecture de Weil. II, Publ. Math. Inst. Hautes Études Sci. 52 (1980), 137–252.CrossRefGoogle Scholar
Dwork, B., Gerotto, G. and Sullivan, F. J., An introduction to G-functions, Annals of Mathematics Studies, vol. 133 (Princeton University Press, Princeton, NJ, 1994).Google Scholar
Faltings, G., $p$-adic Hodge theory, J. Amer. Math. Soc. 1 (1988), 255–299.Google Scholar
Faltings, G., Crystalline cohomology and p-adic Galois-representations, in Algebraic analysis, geometry, and number theory (Baltimore, MD, 1988) (Johns Hopkins University Press, Baltimore, MD, 1989), 25–80.Google Scholar
Faltings, G., F-isocrystals on open varieties: results and conjectures, in The Grothendieck Festschrift, Vol. II, Progress in Mathematics, vol. 87 (Birkhäuser, Boston, MA, 1990), 219–248.Google Scholar
Faltings, G., Almost étale extensions, in Cohomologies p-adiques et applications arithmétiques (II), Astérisque, vol. 279 (Société mathématique de France, 2002), 185–270.Google Scholar
Faltings, G., Coverings of $p$-adic period domains, J. Reine Angew. Math. 643 (2010), 111–139.Google Scholar
Fargues, L., La courbe, in Proceedings of the International Congress of Mathematicians (Rio de Janeiro 2018): Vol. II, Invited lectures (World Scientific Publishing, Hackensack, NJ, 2018), 291–319.Google Scholar
Fontaine, J.-M., Le corps des périodes $p$-adiques, in Périodes p-adiques – Séminaire de Bures sur Yvette, 1988, Astérisque, vol. 223 (Société mathématique de France, 1994), 59–111.Google Scholar
Fontaine, J.-M., Représentations $p$-adiques semi-stables, in Périodes p-adiques – Séminaire de Bures sur Yvette, 1988, Astérisque, vol. 223 (Société mathématique de France, 1994), 113–184.Google Scholar
Fontaine, J.-M., Représentations $\ell$-adiques potentiellement semi-stables, in Périodes p-adiques – Séminaire de Bures sur Yvette, 1988, Astérisque, vol. 223 (Société mathématique de France, 1994), 321–347.Google Scholar
Hartl, U., On a conjecture of Rapoport and Zink, Invent. Math. 193 (2013), 627–696.CrossRefGoogle Scholar
Houzel, C., Géométrie analytique locale, II. Théorie des morphismes finis, Séminaire Henri Cartan 13 (1960–1961), talk no. 19.Google Scholar
Huber, R., A generalization of formal schemes and rigid analytic varieties, Math. Z. 217 (1994), 513–551.CrossRefGoogle Scholar
Huber, R., Étale cohomology of rigid analytic varieties and adic spaces, Aspects of Mathematics, vol. E30 (Friedr. Vieweg & Sohn, Braunschweig, 1996).CrossRefGoogle Scholar
Hyodo, O., On variation of Hodge-Tate structures, Math. Ann. 284 (1989), 7–22.CrossRefGoogle Scholar
Imai, N. and Mieda, Y., Potentially good reduction loci of Shimura varieties, Tunis. J. Math. 2 (2020), 399–454.CrossRefGoogle Scholar
Jannsen, U., On the Galois cohomology of ℓ-adic representations attached to varieties over local or global fields, in Séminaire de Théorie des Nombres, Paris 1986–87, Progress in Mathematics, vol. 75 (Birkhäuser, Boston, MA, 1988), 165–182.Google Scholar
Jannsen, U., Weights in arithmetic geometry, Jpn. J. Math. 5 (2010), 73–102.CrossRefGoogle Scholar
Katz, N. M., Nilpotent connections and the monodromy theorem: applications of a result of Turrittin, Publ. Math. Inst. Hautes Études Sci. 39 (1970), 175–232.CrossRefGoogle Scholar
Katz, N. M., Travaux de Dwork, in Séminaire Bourbaki, 24ème année (1971/1972), Exp. No. 409, Lecture Notes in Mathematics, vol. 317 (Springer, Berlin, 1973), 167–200.Google Scholar
Katz, N. M. and Messing, W., Some consequences of the Riemann hypothesis for varieties over finite fields, Invent. Math. 23 (1974), 73–77.CrossRefGoogle Scholar
Kedlaya, K. S., p-adic differential equations, Cambridge Studies in Advanced Mathematics, vol. 125 (Cambridge University Press, Cambridge, 2010).CrossRefGoogle Scholar
Kedlaya, K. S., Relative p-adic Hodge theory and Rapoport-Zink period domains, in Proceedings of the International Congress of Mathematicians. Volume II (Hindustan Book Agency, New Delhi, 2010), 258–279.Google Scholar
Kedlaya, K. S. and Liu, R., Relative $p$-adic Hodge theory: foundations, Astérisque 371 (2015), 239.Google Scholar
Kisin, M., Local constancy in $p$-adic families of Galois representations, Math. Z. 230 (1999), 569–593.CrossRefGoogle Scholar
Lawrence, B. and Li, S., A counterexample to an optimistic guess about étale local systems, C. R. Math. 359 (2021), 923–924 (en).Google Scholar
Liu, R. and Zhu, X., Rigidity and a Riemann-Hilbert correspondence for $p$-adic local systems, Invent. Math. 207 (2017), 291–343.CrossRefGoogle Scholar
Mokrane, A., La suite spectrale des poids en cohomologie de Hyodo-Kato, Duke Math. J. 72 (1993), 301–337.CrossRefGoogle Scholar
Morita, K., Crystalline and semi-stable representations in the imperfect residue field case, Asian J. Math. 18 (2014), 143–157.CrossRefGoogle Scholar
Nakkajima, Y., $p$-adic weight spectral sequences of log varieties, J. Math. Sci. Univ. Tokyo 12 (2005), 513–661.Google Scholar
Nakkajima, Y., Signs in weight spectral sequences, monodromy-weight conjectures, log Hodge symmetry and degenerations of surfaces, Rend. Semin. Mat. Univ. Padova 116 (2006), 71–185.Google Scholar
Noot, R., The $p$-adic representation of the Weil-Deligne group associated to an abelian variety, J. Number Theory 172 (2017), 301–320.CrossRefGoogle Scholar
Ochiai, T., $l$-independence of the trace of monodromy, Math. Ann. 315 (1999), 321–340.Google Scholar
Ohkubo, S., The $p$-adic monodromy theorem in the imperfect residue field case, Algebra Number Theory 7 (2013), 1977–2037.CrossRefGoogle Scholar
Rapoport, M. and Zink, Th., Über die lokale Zetafunktion von Shimuravarietäten. Monodromiefiltration und verschwindende Zyklen in ungleicher Charakteristik, Invent. Math. 68 (1982), 21–101.CrossRefGoogle Scholar
Saito, T., Weight spectral sequences and independence of $\ell$, J. Inst. Math. Jussieu 2 (2003), 583–634.CrossRefGoogle Scholar
Schneider, P., Nonarchimedean functional analysis, Springer Monographs in Mathematics (Springer, Berlin, 2002).CrossRefGoogle Scholar
Scholze, P., Perfectoid spaces, Publ. Math. Inst. Hautes Études Sci. 116 (2012), 245–313.CrossRefGoogle Scholar
Scholze, P., $p$-adic Hodge theory for rigid-analytic varieties, Forum Math. Pi 1 (2013), e1.CrossRefGoogle Scholar
Scholze, P., $p$-adic Hodge theory for rigid-analytic varieties—corrigendum, Forum Math. Pi 4 (2016), e6.CrossRefGoogle Scholar
Grothendieck, A., Revêtements étales et groupe fondamental, Séminaire de Géométrie Algébrique du Bois-Marie 1960–1961 (SGA 1), Lecture Notes in Mathematics, vol. 224 (Springer, Berlin, 1971).CrossRefGoogle Scholar
Grothendieck, A., Groupes de monodromie en géométrie algébrique I, Séminaire de Géométrie Algébrique du Bois-Marie 1967–1969 (SGA 7 I), Lecture Notes in Mathematics, vol. 288 (Springer, Berlin, 1972).Google Scholar
Shimizu, K., Constancy of generalized Hodge-Tate weights of a local system, Compos. Math. 154 (2018), 2606–2642.CrossRefGoogle Scholar
Tan, F. and Tong, J., Crystalline comparison isomorphisms in $p$-adic Hodge theory: the absolutely unramified case, Algebra Number Theory 13 (2019), 1509–1581.CrossRefGoogle Scholar
Tsuji, T., Crsytalline sheaves and filtered convergent $F$-isocrystals on log schemes, Preprint.Google Scholar
Tsuji, T., $p$-adic étale cohomology and crystalline cohomology in the semi-stable reduction case, Invent. Math. 137 (1999), 233–411.CrossRefGoogle Scholar
Tsuji, T., Semi-stable conjecture of Fontaine-Jannsen: a survey, in Cohomologies $p$-adiques et applications arithmétiques (II), Astérisque, vol. 279 (Société mathématique de France, 2002), 323–370.Google Scholar