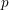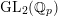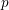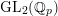Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Hu, Yongquan
and
Paškūnas, Vytautas
2019.
On crystabelline deformation rings of $$\mathrm {Gal}(\overline{\mathbb {Q}}_p/\mathbb {Q}_p)$$ Gal ( Q ¯ p / Q p ) (with an appendix by Jack Shotton).
Mathematische Annalen,
Vol. 373,
Issue. 1-2,
p.
421.
Tung, Shen-Ning
2021.
On the modularity of 2-adic potentially semi-stable deformation rings.
Mathematische Zeitschrift,
Vol. 298,
Issue. 1-2,
p.
107.
Tung, Shen-Ning
2021.
On the automorphy of 2-dimensional potentially
semistable deformation rings of Gℚp.
Algebra & Number Theory,
Vol. 15,
Issue. 9,
p.
2173.
Dotto, Andrea
and
Le, Daniel
2021.
Diagrams in the mod p cohomology of Shimura curves.
Compositio Mathematica,
Vol. 157,
Issue. 8,
p.
1653.
Hu, Yong Quan
2021.
A Note on Integral Structures in Some Locally Algebraic Representations of GL2.
Acta Mathematica Sinica, English Series,
Vol. 37,
Issue. 1,
p.
59.
Gee, Toby
and
Newton, James
2022.
PATCHING AND THE COMPLETED HOMOLOGY OF LOCALLY SYMMETRIC SPACES.
Journal of the Institute of Mathematics of Jussieu,
Vol. 21,
Issue. 2,
p.
395.
Paškūnas, Vytautas
2022.
ON SOME CONSEQUENCES OF A THEOREM OF J. LUDWIG.
Journal of the Institute of Mathematics of Jussieu,
Vol. 21,
Issue. 3,
p.
1067.
Nakamura, Kentaro
2023.
Zeta morphisms for rank two universal deformations.
Inventiones mathematicae,
Vol. 234,
Issue. 1,
p.
171.
Caraiani, Ana
and
Tamiozzo, Matteo
2023.
On the étale cohomology of Hilbert modular varieties with torsion coefficients.
Compositio Mathematica,
Vol. 159,
Issue. 11,
p.
2279.
Hu, Yongquan
and
Wang, Haoran
2024.
On some mod p representations of quaternion algebra over ℚp.
Compositio Mathematica,
Vol. 160,
Issue. 11,
p.
2585.
Banerjee, Debargha
and
Rai, Vivek
2024.
Towards a mod-p Lubin–Tate theory for GL2 over totally real fields.
International Journal of Number Theory,
Vol. 20,
Issue. 01,
p.
199.
Le, Daniel
Hung, Bao
Morra, Stefano
Park, Chol
and
Qian, Zicheng
2025.
Moduli of Fontaine–Laffaille Representations and a mod-𝑝 Local-Global Compatibility Result.
Memoirs of the American Mathematical Society,
Vol. 312,
Issue. 1584,
Tarrach, Guillem
2025.
The p-arithmetic homology of mod p representations of GL 2 (ℚ p ).
Journal de théorie des nombres de Bordeaux,
Vol. 37,
Issue. 1,
p.
299.