Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-26T09:42:45.110Z Has data issue: false hasContentIssue false
  • English
  • Français

Projective objects and the modified trace in factorisable finite tensor categories

Part of: Categories and geometry Lie algebras and Lie superalgebras Categories with structure Homological algebra

Published online by Cambridge University Press:  26 March 2020

Azat M. Gainutdinov  and
Ingo Runkel
Azat M. Gainutdinov
Affiliation:
Institut Denis Poisson, CNRS, Université de Tours, Université d’Orléans, Parc de Grandmont, 37200Tours, France email azat.gainutdinov@lmpt.univ-tours.fr Fachbereich Mathematik, Universität Hamburg, Bundesstraße 55, 20146Hamburg, Germany
Ingo Runkel
Affiliation:
Fachbereich Mathematik, Universität Hamburg, Bundesstraße 55, 20146Hamburg, Germany email ingo.runkel@uni-hamburg.de
Get access Rights & Permissions [Opens in a new window]

Abstract

For 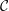${\mathcal{C}}$ a factorisable and pivotal finite tensor category over an algebraically closed field of characteristic zero we show:

  1. (1) 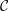${\mathcal{C}}$ always contains a simple projective object;

  2. (2) if 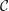${\mathcal{C}}$ is in addition ribbon, the internal characters of projective modules span a submodule for the projective 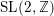$\text{SL}(2,\mathbb{Z})$-action;

  3. (3) the action of the Grothendieck ring of 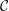${\mathcal{C}}$ on the span of internal characters of projective objects can be diagonalised;

  4. (4) the linearised Grothendieck ring of 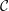${\mathcal{C}}$ is semisimple if and only if 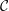${\mathcal{C}}$ is semisimple.

Results (1)–(3) remain true in positive characteristic under an extra assumption. Result (1) implies that the tensor ideal of projective objects in 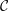${\mathcal{C}}$ carries a unique-up-to-scalars modified trace function. We express the modified trace of open Hopf links coloured by projectives in terms of 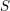$S$-matrix elements. Furthermore, we give a Verlinde-like formula for the decomposition of tensor products of projective objects which uses only the modular 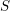$S$-transformation restricted to internal characters of projective objects. We compute the modified trace in the example of symplectic fermion categories, and we illustrate how the Verlinde-like formula for projective objects can be applied there.

Keywords

braided and pivotal categoriesprojective objectsmodified tracesGrothendieck ringsvertex-operator algebrasVerlinde-like formula

MSC classification

Primary: 18D10: Monoidal categories (= multiplicative categories), symmetric monoidal categories, braided categories 18G05: Projectives and injectives 18F30: Grothendieck groups 17B69: Vertex operators; vertex operator algebras and related structures
Type
Research Article
Information
Compositio Mathematica , Volume 156 , Issue 4 , April 2020 , pp. 770 - 821
Copyright
© The Authors 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abe, T., A ℤ2 -orbifold model of the symplectic fermionic vertex operator superalgebra, Math. Z. 255 (2007), 755–792.CrossRefGoogle Scholar
Andruskiewitsch, N., Angiono, I., Garcia Iglesias, A., Torrecillas, B. and Vay, C., From Hopf algebras to tensor categories, in Conformal field theories and tensor categories, Mathematical Lectures from Peking University (Springer, Heidelberg, 2014), 1–31.Google Scholar
Arike, Y. and Nagatomo, K., Some remarks on pseudo-trace functions for orbifold models associated with symplectic fermions, Int. J. Math. 24 (2013), 1350008.CrossRefGoogle Scholar
Bakalov, B. and Kirillov, A. A., Lectures on tensor categories and modular functors (American Mathematical Society, Providence, RI, 2001).Google Scholar
Bartlett, B., Douglas, C. L., Schommer-Pries, C. J. and Vicary, J., Modular categories as representations of the 3-dimensional bordism 2-category, Preprint (2015), arXiv:1509.06811 [math.AT].Google Scholar
Broué, M., Higman’s criterion revisited, Michigan Math. J. 58 (2009), 125–179.CrossRefGoogle Scholar
Cohen, M. and Westreich, S., Characters and a Verlinde-type formula for symmetric Hopf algebras, J. Algebra 320 (2008), 4300–4316.CrossRefGoogle Scholar
Costantino, F., Geer, N. and Patureau-Mirand, B., Some remarks on the unrolled quantum group of sl(2), J. Pure Appl. Algebra 219 (2015), 3238–3262.CrossRefGoogle Scholar
Creutzig, T. and Gannon, T., Logarithmic conformal field theory, log-modular tensor categories and modular forms, J. Phys. A50 (2017), 404004.Google Scholar
Davydov, A. and Runkel, I., ℤ/2ℤ-extensions of Hopf algebra module categories by their base categories, Adv. Math. 247 (2013), 192–265.CrossRefGoogle Scholar
Davydov, A. and Runkel, I., A braided monoidal category for symplectic fermions, in Proceedings of the XXIX international colloquium on group-theoretical methods in physics, Tianjin, August 2012, Nankai Series in Pure, Applied Mathematics and Theoretical Physics, vol. 11 (World Scientific, 2013), 399–404.Google Scholar
Davydov, A. and Runkel, I., Holomorphic symplectic fermions, Math. Z. 285 (2017), 967–1006.CrossRefGoogle Scholar
Deligne, P., La catégorie des représentations du groupe symétrique S t, lorsque t n’est pas un entier naturel, in Algebraic groups and homogeneous spaces, Mumbai, 2004 (TIFR, 2007), 209–273.Google Scholar
Drinfeld, V. G., On almost cocommutative Hopf algebras, Leningrad Math. J. 1 (1990), 321–342.Google Scholar
Etingof, P. I., Gelaki, S., Nikshych, D. and Ostrik, V., Tensor categories, Mathematical Surveys and Monographs, vol. 205 (American Mathematical Society, Providence, RI, 2015).CrossRefGoogle Scholar
Etingof, P. I., Nikshych, D. and Ostrik, V., An analogue of Radford’s S 4 formula for finite tensor categories, Int. Math. Res. Not. IMRN 54 (2004), 2915–2933.CrossRefGoogle Scholar
Etingof, P. I. and Ostrik, V., Finite tensor categories, Mosc. Math. J. 4 (2004), 627–654.CrossRefGoogle Scholar
Farsad, V., Gainutdinov, A. M. and Runkel, I., The symplectic fermion ribbon quasi-Hopf algebra and the $\text{SL}(2,\mathbb{Z})$-action on its centre, Preprint (2017), arXiv:1706.08164 [math.QA].Google Scholar
Farsad, V., Gainutdinov, A. M. and Runkel, I., SL(2, ℤ)-action for ribbon quasi-Hopf algebras, J. Algebra 522 (2019), 243–308.CrossRefGoogle Scholar
Feigin, B. L., Gainutdinov, A. M., Semikhatov, A. M. and Tipunin, I. Y., Modular group representations and fusion in logarithmic conformal field theories and in the quantum group center, Comm. Math. Phys. 265 (2006), 47–93.CrossRefGoogle Scholar
Fuchs, J., On non-semisimple fusion rules and tensor categories, Contemp. Math. 442 (2007), 315–337.CrossRefGoogle Scholar
Fuchs, J., Hwang, S., Semikhatov, A. M. and Tipunin, I. Y., Nonsemisimple fusion algebras and the Verlinde formula, Comm. Math. Phys. 247 (2004), 713–742.CrossRefGoogle Scholar
Fuchs, J. and Schweigert, C., Hopf algebras and finite tensor categories in conformal field theory, Rev. Un. Mat. Argentina 51 (2010), 43–90.Google Scholar
Fuchs, J. and Schweigert, C., Consistent systems of correlators in non-semisimple conformal field theory, Adv. Math. 307 (2017), 598–639.CrossRefGoogle Scholar
Fuchs, J., Schweigert, C. and Stigner, C., From non-semisimple Hopf algebras to correlation functions for logarithmic CFT, J. Phys. A 46 (2013), 494008.Google Scholar
Gaberdiel, M. R. and Kausch, H. G., A rational logarithmic conformal field theory, Phys. Lett. B 386 (1996), 131–137.CrossRefGoogle Scholar
Gainutdinov, A. M. and Runkel, I., Symplectic fermions and a quasi-Hopf algebra structure on Uisℓ (2), J. Algebra 476 (2017), 415–458.CrossRefGoogle Scholar
Gainutdinov, A. M. and Runkel, I., The non-semisimple Verlinde formula and pseudo-trace functions, J. Pure Appl. Algebra 223 (2019), 660–690.CrossRefGoogle Scholar
Geer, N., Kujawa, J. and Patureau-Mirand, B., Generalized trace and modified dimension functions on ribbon categories, Selecta Math. (N.S.) 17 (2011), 453–504.CrossRefGoogle Scholar
Geer, N., Kujawa, J. and Patureau-Mirand, B., Ambidextrous objects and trace functions for nonsemisimple categories, Proc. Amer. Math. Soc. 141 (2013), 2963–2978.CrossRefGoogle Scholar
Geer, N., Patureau-Mirand, B. and Turaev, V., Modified quantum dimensions and re-normalized link invariants, Compos. Math. 145 (2009), 196–212.CrossRefGoogle Scholar
Geer, N., Patureau-Mirand, B. and Virelizier, A., Traces on ideals in pivotal categories, Quantum Topol. 4 (2013), 91–124.CrossRefGoogle Scholar
Hesse, J., An equivalence between Frobenius algebras and Calabi–Yau categories, J. Homotopy Relat. Struct. 13 (2017), 251–272.CrossRefGoogle Scholar
Héthelyi, L., Horváth, E., Külshammer, B. and Murray, J., Central ideals and Cartan invariants of symmetric algebras, J. Algebra 293 (2005), 243–260.CrossRefGoogle Scholar
Huang, Y.-Z., Vertex operator algebras and the Verlinde conjecture, Commun. Contemp. Math. 10 (2008), 103.CrossRefGoogle Scholar
Huang, Y.-Z., Rigidity and modularity of vertex tensor categories, Commun. Contemp. Math. 10 (2008), 871–911.CrossRefGoogle Scholar
Huang, Y.-Z., Cofiniteness conditions, projective covers and the logarithmic tensor product theory, J. Pure Appl. Algebra 213 (2009), 458–475.CrossRefGoogle Scholar
Huang, Y.-Z., Representations of vertex operator algebras and braided finite tensor categories, Contemp. Math. 497 (2009), 97–112.CrossRefGoogle Scholar
Huang, Y.-Z., Lepowsky, J. and Zhang, L., Logarithmic tensor category theory for generalized modules for a conformal vertex algebra, I–VIII, Preprint (2010), arXiv:1012.4193, arXiv:1012.4196, arXiv:1012.4197, arXiv:1012.4198, arXiv:1012.4199, arXiv:1012.4202, arXiv:1110.1929, arXiv:1110.1931.Google Scholar
Kausch, H.G., Curiosities at $c=-2$, Preprint (1995), arXiv:hep-th/9510149.Google Scholar
Kerler, T., Mapping class group action on quantum doubles, Comm. Math. Phys. 168 (1995), 353–388.CrossRefGoogle Scholar
Kerler, T., Genealogy of nonperturbative quantum-invariants of 3-manifolds: The surgical family, in Quantum invariants and low-dimensional topology, eds Andersen, J. E. et al. (Dekker, New York, NY, 1997), 503–547.Google Scholar
Kerler, T. and Lyubashenko, V. V., Non-semisimple topological quantum field theories for 3-manifolds with corners, Lecture Notes in Mathematics, vol. 1765 (Springer, 2001).Google Scholar
Kondo, H. and Saito, Y., Indecomposable decomposition of tensor products of modules over the restricted quantum universal enveloping algebra associated to sl(2), J. Algebra 330 (2011), 103–129.CrossRefGoogle Scholar
Lachowska, A., On the center of the small quantum group, J. Algebra 262 (2003), 313–331.CrossRefGoogle Scholar
Lachowska, A., A counterpart of the Verlinde algebra for the small quantum group, Duke Math. J. 118 (2003), 37–60.CrossRefGoogle Scholar
Liu, Y., Zhou, G. and Zimmermann, A., Higman ideal, stable Hochschild homology and Auslander–Reiten conjecture, Math. Z. 270 (2012), 759–781.CrossRefGoogle Scholar
Lorenz, M., Representations of finite-dimensional hopf algebras, J. Algebra 188 (1997), 476–505.CrossRefGoogle Scholar
Lyubashenko, V. V., Modular transformations for tensor categories, J. Pure Appl. Algebra 98 (1995), 279–327.CrossRefGoogle Scholar
Lyubashenko, V. V., Invariants of three manifolds and projective representations of mapping class groups via quantum groups at roots of unity, Comm. Math. Phys. 172 (1995), 467–516.CrossRefGoogle Scholar
Lyubashenko, V. V. and Majid, S., Braided groups and quantum fourier transform, J. Algebra 166 (1994), 506–528.CrossRefGoogle Scholar
Mac Lane, S., Categories for the working mathematician, second edition (Springer, 1998).Google Scholar
Miyamoto, M., Modular invariance of vertex operator algebras satisfying C (2) cofiniteness, Duke Math. J. 122 (2004), 51–91.CrossRefGoogle Scholar
Nagatomo, K. and Tsuchiya, A., The triplet vertex operator algebra W (p) and the restricted quantum group at root of unity, in Exploring new structures and natural constructions in mathematical physics, Advanced Studies in Pure Mathematics, vol. 61, eds Hasegawa, K. et al. (Mathematical Society of Japan, 2011).Google Scholar
Radford, D. E., The trace function and Hopf algebras, J. Algebra 163 (1994), 583–622.CrossRefGoogle Scholar
Reshetikhin, N. and Turaev, V. G., Invariants of 3-manifolds via link polynomials and quantum groups, Invent. Math. 103 (1991), 547–597.CrossRefGoogle Scholar
Runkel, I., A braided monoidal category for free super-bosons, J. Math. Phys. 55 (2014), 041702.CrossRefGoogle Scholar
Serre, J.-P., Linear representations of finite groups (Springer, 1977).CrossRefGoogle Scholar
Shimizu, K., On unimodular finite tensor categories, Int. Math. Res. Not. IMRN 2017 (2017), 277–322.Google Scholar
Shimizu, K., The monoidal center and the character algebra, J. Pure Appl. Algebra 221 (2017), 2338–2371.CrossRefGoogle Scholar
Shimizu, K., Non-degeneracy conditions for braided finite tensor categories, Adv. Math. 355 (2019), 106778.CrossRefGoogle Scholar
Tsuchiya, A. and Wood, S., The tensor structure on the representation category of the W p triplet algebra, J. Phys. A46 (2013), 445203.Google Scholar
Turaev, V. G., Quantum invariants of knots and 3-manifolds (de Gruyter, 1994).CrossRefGoogle Scholar
Verlinde, E. P., Fusion rules and modular transformations in 2D conformal field theory, Nuclear Phys. B 300 (1988), 360–376.CrossRefGoogle Scholar
Zhu, Y.-C., Modular invariance of vertex operator algebras, J. Amer. Math. Soc. 9 (1996), 237–302.CrossRefGoogle Scholar