Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-10T21:18:39.166Z Has data issue: false hasContentIssue false
  • English
  • Français

Purity for graded potentials and quantum cluster positivity

Part of: Cycles and subschemes Singularities Projective and enumerative geometry Arithmetic rings and other special rings

Published online by Cambridge University Press:  19 May 2015

Ben Davison ,
Davesh Maulik ,
Jörg Schürmann  and
Balázs Szendrői
Ben Davison
Affiliation:
GEOM, EPFL Lausanne, Switzerland email nicholas.davison@epfl.ch
Davesh Maulik
Affiliation:
Department of Mathematics, Columbia University, USA email dmaulik@math.columbia.edu
Jörg Schürmann
Affiliation:
Mathematisches Institut, Universität Münster, Germany email jschuerm@math.uni-muenster.de
Balázs Szendrői
Affiliation:
Mathematical Institute, University of Oxford, UK email szendroi@maths.ox.ac.uk
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Consider a smooth quasi-projective variety 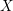$X$ equipped with a 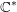$\mathbb{C}^{\ast }$-action, and a regular function 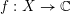$f:X\rightarrow \mathbb{C}$ which is 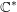$\mathbb{C}^{\ast }$-equivariant with respect to a positive weight action on the base. We prove the purity of the mixed Hodge structure and the hard Lefschetz theorem on the cohomology of the vanishing cycle complex of 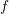$f$ on proper components of the critical locus of 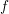$f$, generalizing a result of Steenbrink for isolated quasi-homogeneous singularities. Building on work by Kontsevich and Soibelman, Nagao, and Efimov, we use this result to prove the quantum positivity conjecture for cluster mutations for all quivers admitting a positively graded nondegenerate potential. We deduce quantum positivity for all quivers of rank at most 4; quivers with nondegenerate potential admitting a cut; and quivers with potential associated to triangulations of surfaces with marked points and nonempty boundary.

Keywords

vanishing cycle sheafpurity of mixed Hodge structurecluster algebraquantum cluster positivity

MSC classification

Primary: 14C30: Transcendental methods, Hodge theory , Hodge conjecture 32S35: Mixed Hodge theory of singular varieties 14N35: Gromov-Witten invariants, quantum cohomology, Gopakumar-Vafa invariants, Donaldson-Thomas invariants 13F60: Cluster algebras
Type
Research Article
Information
Compositio Mathematica , Volume 151 , Issue 10 , October 2015 , pp. 1913 - 1944
Copyright
© The Authors 2015 

References

Amiot, C. and Oppermann, S., Cluster equivalence and graded derived equivalence, Doc. Math. 19 (2014), 1155–1206.CrossRefGoogle Scholar
Banagl, M., Budur, N. and Maxim, L., Intersection spaces, perverse sheaves and type IIB string theory, Adv. Theor. Math. Phys. 18 (2014), 363–399.CrossRefGoogle Scholar
Behrend, K., Donaldson–Thomas type invariants via microlocal geometry, Ann. of Math. (2) 170 (2009), 1307–1338.CrossRefGoogle Scholar
Berenstein, A. and Zelevinsky, A., Quantum cluster algebras, Adv. Math. 195 (2005), 405–455.CrossRefGoogle Scholar
Bridgeland, T., Equivalences of triangulated categories and Fourier–Mukai transforms, Bull. Lond. Math. Soc. 31 (1999), 25–34.CrossRefGoogle Scholar
Bridgeland, T., Stability conditions on triangulated categories, Ann. of Math. (2) 166 (2007), 317–345.CrossRefGoogle Scholar
Buan, A., Iyama, O., Rieten, I. and Smith, D., Mutation of cluster-tilting objects and potentials, Amer. J. Math. 133 (2011), 835–887.CrossRefGoogle Scholar
Denef, J. and Loeser, F., Motivic exponential integrals and a motivic Thom–Sebastiani theorem, Duke Math. J. 99 (1999), 285–309.CrossRefGoogle Scholar
Derksen, H., Weyman, J. and Zelevinsky, A., Quivers with potentials and their representations I: Mutations, Selecta Math. (N.S.) 14 (2008), 59–119.CrossRefGoogle Scholar
Dimca, A. and Szendrői, B., The Milnor fibre of the Pfaffian and the Hilbert scheme of four points on ℂ3, Math. Res. Lett. 16 (2009), 1037–1055.CrossRefGoogle Scholar
Efimov, A., Quantum cluster variables via vanishing cycles, Preprint (2011), arXiv:1112.3601.Google Scholar
Fomin, S., Shapiro, M. and Thurston, D., Cluster algebras and triangulated surfaces. Part I: Cluster complexes, Acta Math. 201 (2008), 83–146.CrossRefGoogle Scholar
Fomin, S. and Zelevinsky, A., Cluster algebras I: Foundations, J. Amer. Math. Soc. 15 (2002), 497–529.CrossRefGoogle Scholar
Fordy, A. P. and Marsh, R. J., Cluster mutation-periodic quivers and associated Laurent sequences, J. Algebraic Combin. 34 (2011), 19–66.CrossRefGoogle Scholar
Geiß, C., Labardini-Fragoso, D. and Schröer, J., The representation type of Jacobian algebras, Preprint (2013), arXiv:1308.0478.Google Scholar
Geiß, C., Leclerc, B. and Schröer, J., Preprojective algebras and cluster algebras, in Trends in representation theory of algebras and related topics, EMS Series of Congress Reports, ed. Skowroński, A. (European Mathematical Society, Zurich, 2008), 253–283.CrossRefGoogle Scholar
Ginzburg, V., Calabi–Yau algebras, Preprint (2006), arXiv:0612139.Google Scholar
Guibert, G., Loeser, F. and Merle, M., Iterated vanishing cycles, convolution, and a motivic analogue of a conjecture of Steenbrink, Duke Math. J. 132 (2006), 409–457.CrossRefGoogle Scholar
Katzarkov, L., Kontsevich, M. and Pantev, T., Hodge theoretic aspects of mirror symmetry, in From Hodge theory to integrability and TQFT tt∗-geometry, Proceedings of Symposia in Pure Mathematics, vol. 78 (American Mathematical Society, Providence, RI, 2008), 87–174.CrossRefGoogle Scholar
Keller, B., Cluster algebras, quiver representations and triangulated categories, in Triangulated categories, London Mathematical Society Lecture Note Series, vol. 375 (Cambridge University Press, Cambridge, 2010), 76–160.CrossRefGoogle Scholar
Keller, B. and Yang, D., Derived equivalences from mutations of quivers with potential, Adv. Math. 226 (2011), 2118–2168.CrossRefGoogle Scholar
Kimura, Y. and Qin, F., Graded quiver varieties, quantum cluster algebras and dual canonical basis, Adv. Math. 262 (2014), 261–312.CrossRefGoogle Scholar
King, A., Moduli of representations of finite dimensional algebras, Q. J. Math. 45 (1994), 515–530.CrossRefGoogle Scholar
Kontsevich, M. and Soibelman, Y., Stability structures, motivic Donaldson–Thomas invariants and cluster transformations, Preprint (2008), arXiv:0811.2435.Google Scholar
Kontsevich, M. and Soibelman, Y., Cohomological Hall algebra, exponential Hodge structures and motivic Donaldson–Thomas invariants, Commun. Number Theory Phys. 5 (2011), 231–352.CrossRefGoogle Scholar
Kulikov, V. S., Mixed Hodge structures and singularities, Cambridge Tracts in Mathematics, vol. 132 (Cambridge University Press, Cambridge, 1998).Google Scholar
Labardini-Fragoso, D., Quivers with potentials associated to triangulated surfaces, Proc. Lond. Math. Soc. (3) 98 (2009), 797–839.CrossRefGoogle Scholar
Le Bruyn, L. and Procesi, C., Semisimple representations of quivers, Trans. Amer. Math. Soc. 32 (1990), 585–598.CrossRefGoogle Scholar
Lee, K. and Schiffler, R., Positivity for cluster algebras, Ann. of Math. (2) 182 (2015), 73–125.CrossRefGoogle Scholar
Mozgovoy, S. and Reineke, M., On the noncommutative Donaldson–Thomas invariants arising from brane tilings, Adv. Math. 223 (2010), 1521–1544.CrossRefGoogle Scholar
Musiker, G., Schiffler, R. and Williams, L., Positivity for cluster algebras from surfaces, Adv. Math. 227 (2011), 2241–2308.CrossRefGoogle Scholar
Nagao, K., Donaldson–Thomas theory and cluster algebras, Duke Math. J. 162 (2013), 1313–1367.CrossRefGoogle Scholar
Nagao, K. and Nakajima, H., Counting invariant of perverse coherent sheaves and its wall-crossing, Int. Math. Res. Not. IMRN 2011 3885–3938.Google Scholar
Nakajima, H., Quiver varieties and cluster algebras, Kyoto J. Math. 51 (2011), 71–126.CrossRefGoogle Scholar
Navarro Aznar, V., Sur la théorie de Hodge–Deligne, Invent. Math. 90 (1987), 11–76.CrossRefGoogle Scholar
Plamondon, P., Cluster characters for cluster categories with infinite-dimensional morphism spaces, Adv. Math. 227 (2011), 1–39.CrossRefGoogle Scholar
Saito, M., Modules de Hodge polarisables, Publ. Res. Inst. Math. Sci. 24 (1988), 849–995.CrossRefGoogle Scholar
Saito, M., Mixed Hodge modules, Publ. Res. Inst. Math. Sci. 26 (1990), 221–333.CrossRefGoogle Scholar
Saito, M., Thom–Sebastiani theorem for mixed Hodge modules, Preprint (1990/2011).Google Scholar
Scherk, J. and Steenbrink, J., On the mixed Hodge structure on the cohomology of the milnor fibre, Math. Ann. 271 (1985), 641–665.CrossRefGoogle Scholar
Schmid, W., Variation of Hodge structures: the singularities of the period mapping, Invent. Math. 22 (1973), 211–319.CrossRefGoogle Scholar
Speyer, D. E., Perfect matchings and the octahedron recurrence, J. Algebraic Combin. 25 (2007), 309–348.CrossRefGoogle Scholar
Steenbrink, J., Limits of Hodge structures, Invent. Math. 31 (1976), 229–257.CrossRefGoogle Scholar
Steenbrink, J., Intersection form for quasi-homogeneous singularities, Comput. Math. 34 (1977), 211–223.Google Scholar
Steenbrink, J., Mixed Hodge structure on the vanishing cohomology, in Real and complex singularities (Sijthoff and Noordhoff, Alphen aan den Rijn, 1977), 525–563.Google Scholar
Szendrői, B., Nekrasov’s partition function and refined Donaldson–Thomas theory: the rank one case, SIGMA Symmetry Integrability Geom. Methods Appl. (2012), 088.Google Scholar
Thuong, L. Q., Proofs of the integral identity conjecture over algebraically closed fields, Preprint (2012), arXiv:1206.5334.Google Scholar