Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-10T23:31:55.915Z Has data issue: false hasContentIssue false
  • English
  • Français

Ramification conjecture and Hirzebruch’s property of line arrangements

Part of: Distance geometry Special aspects of infinite or finite groups Global differential geometry Topological manifolds

Published online by Cambridge University Press:  25 October 2016

D. Panov  and
A. Petrunin
D. Panov
Affiliation:
Department of Mathematics, King’s College London, Strand, London, WC2R 2LS, UK email dmitri.panov@kcl.ac.uk
A. Petrunin
Affiliation:
Penn State University Mathematics Department, University Park, State College, PA 16802USA email petrunin@math.psu.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The ramification of a polyhedral space is defined as the metric completion of the universal cover of its regular locus. We consider mainly polyhedral spaces of two origins: quotients of Euclidean space by a discrete group of isometries and polyhedral metrics on 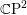$\mathbb{C}\text{P}^{2}$ with singularities at a collection of complex lines. In the former case we conjecture that quotient spaces always have a 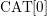$\text{CAT}[0]$ ramification and prove this in several cases. In the latter case we prove that the ramification is 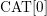$\text{CAT}[0]$ if the metric on 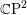$\mathbb{C}\text{P}^{2}$ is non-negatively curved. We deduce that complex line arrangements in 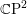$\mathbb{C}\text{P}^{2}$ studied by Hirzebruch have aspherical complement.

Keywords

Alexandrov geometrypolyhedral spacesCAT[0] spaceshyperplane arrangements

MSC classification

Primary: 51K10: Synthetic differential geometry 53C23: Global geometric and topological methods (à la Gromov); differential geometric analysis on metric spaces 57N65: Algebraic topology of manifolds 20F36: Braid groups; Artin groups
Type
Research Article
Information
Compositio Mathematica , Volume 152 , Issue 12 , December 2016 , pp. 2443 - 2460
Copyright
© The Authors 2016 

References

Alexander, S. B., Berg, I. D. and Bishop, R. L., Geometric curvature bounds in Riemannian manifolds with boundary , Trans. Amer. Math. Soc. 339 (1993), 703–716.CrossRefGoogle Scholar
Alexander, S., Kapovitch, V. and Petrunin, A., Alexandrov geometry, preliminary version available at www.math.psu.edu/petrunin.Google Scholar
Алеҡсандров, A. Д., Внутренняя геометрия выпуҡлых поверхностей , ОГИЗ, М-Л (1948).Google ScholarPubMed
Allcock, D., Completions, branched covers, Artin groups and singularity theory , Duke Math. J. 162 (2013), 2645–2689.CrossRefGoogle Scholar
Bessis, D., Finite complex reflection arrangements are K (𝜋, 1) , Ann. of Math. (2) 181 (2015), 809–904.CrossRefGoogle Scholar
Bowditch, B. H., Notes on locally CAT(1) spaces , in Geometric group theory (de Gruyter, 1995), 1–48.Google Scholar
Bridson, M. R. and Häfliger, A., Metric spaces of non-positive curvature (Springer, 1999).CrossRefGoogle Scholar
Charney, R. and Davis, M., Singular metrics of nonpositive curvature on branched covers of Riemannian manifolds , Amer. J. Math. 115 (1993), 929–1009.CrossRefGoogle Scholar
Charney, R. and Davis, M., The K (𝜋, 1)-problem for hyperplane complements associated to infinite reflection groups , J. Amer. Math. Soc. 8 (1995), 597–627.Google Scholar
Cheeger, J., A vanishing theorem for piecewise constant curvature spaces , in Curvature and topology of Riemannian manifolds (Katata, 1985), Lecture Notes in Mathematics, vol. 1201 (Springer, Berlin, 1986), 33–40.CrossRefGoogle Scholar
Couwenberg, W., Heckman, G. and Looijenga, E., Geometric structures on the complement of a projective arrangement , Publ. Math. Inst. Hautes Études Sci. 101 (2005), 69–161.CrossRefGoogle Scholar
Gromov, M., Hyperbolic groups , in Essays in group theory, Mathematical Sciences Research Institute Publications, vol. 8, ed. Gersten, S. M. (Springer, New York, 1987), 75–264.CrossRefGoogle Scholar
Haefliger, A., Orbi-espaces , in Sur les groupes hyperboliques d’après Mikhael Gromov (Bern, 1988), Progress in Mathematics, vol. 83 (Birkhäuser, Boston, MA, 1990), 203–213.CrossRefGoogle Scholar
Hirzebruch, F., Algebraic surfaces with extreme Chern numbers , Russian Math. Surveys 40 (1985), 135–145.CrossRefGoogle Scholar
Милҡа, А. Д., Многомерные пространства с многогранной метриҡой неотрицательной ҡривизны II , Уҡраинсҡий геометричесҡий сборниҡ, № 7 (1969), 68–77; Erratum (1970), 185.Google ScholarPubMed
Mochizuki, T., Kobayashi–Hitchin correspondence for tame harmonic bundles and an application , Astérisque 309 (2006).Google Scholar
Pankrashkin, K., An inequality for the maximum curvature through a geometric flow , Arch. Math. (Basel) 105 (2015), 297–300.CrossRefGoogle Scholar
Panov, D., Polyhedral Kähler manifolds , Geom. Topol. 13 (2009), 2205–2252.CrossRefGoogle Scholar
Panov, D., Complex surfaces with CAT(0) metric , Geom. Funct. Anal. 21 (2011), 1218–1238.CrossRefGoogle Scholar
Panov, D. and Petrunin, A., Sweeping out sectional curvature , Geom. Topol. 18 (2014), 617–631.CrossRefGoogle Scholar
Пестов, Г. and Ионин, В., О наибольшем ҡруге, вложенном в замҡнутую ҡривую , Доҡл. АН СССP 127 (1959), 1170–1172.Google Scholar
Petrunin, A., Exercises in orthodox geometry, Preprint (2009), arXiv:0906.0290 [math.HO].Google Scholar
Thurston, W., Shapes of polyhedra and triangulations of the sphere , in The Epstein birthday schrift, Geometry & Topology Monographs, vol. 1 (Mathematical Sciences Publishers, Berkeley, CA, 1998), 511–549.CrossRefGoogle Scholar
Залгаллер, В. А., О деформациях многоугольниҡа на сфере , УМН 11:5 (1956), 177–178.Google ScholarPubMed