Article contents
Rank 3 quadratic generators of Veronese embeddings
Published online by Cambridge University Press: 02 August 2021
Abstract
Let 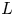 $L$ be a very ample line bundle on a projective scheme
$L$ be a very ample line bundle on a projective scheme 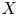 $X$ defined over an algebraically closed field
$X$ defined over an algebraically closed field 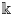 $\Bbbk$ with
$\Bbbk$ with 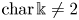 ${\rm char}\,\Bbbk \neq 2$. We say that
${\rm char}\,\Bbbk \neq 2$. We say that 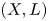 $(X,L)$ satisfies property
$(X,L)$ satisfies property 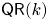 $\mathsf {QR}(k)$ if the homogeneous ideal of the linearly normal embedding
$\mathsf {QR}(k)$ if the homogeneous ideal of the linearly normal embedding 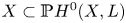 $X \subset {\mathbb {P}} H^{0} (X,L)$ can be generated by quadrics of rank less than or equal to
$X \subset {\mathbb {P}} H^{0} (X,L)$ can be generated by quadrics of rank less than or equal to 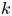 $k$. Many classical varieties, such as Segre–Veronese embeddings, rational normal scrolls and curves of high degree, satisfy property
$k$. Many classical varieties, such as Segre–Veronese embeddings, rational normal scrolls and curves of high degree, satisfy property 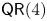 $\mathsf {QR}(4)$. In this paper, we first prove that if
$\mathsf {QR}(4)$. In this paper, we first prove that if 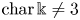 ${\rm char}\,\Bbbk \neq 3$ then
${\rm char}\,\Bbbk \neq 3$ then 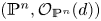 $({\mathbb {P}}^{n} , \mathcal {O}_{{\mathbb {P}}^{n}} (d))$ satisfies property
$({\mathbb {P}}^{n} , \mathcal {O}_{{\mathbb {P}}^{n}} (d))$ satisfies property 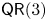 $\mathsf {QR}(3)$ for all
$\mathsf {QR}(3)$ for all 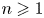 $n \geqslant 1$ and
$n \geqslant 1$ and 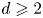 $d \geqslant 2$. We also investigate the asymptotic behavior of property
$d \geqslant 2$. We also investigate the asymptotic behavior of property 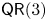 $\mathsf {QR}(3)$ for any projective scheme. Specifically, we prove that (i) if
$\mathsf {QR}(3)$ for any projective scheme. Specifically, we prove that (i) if 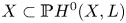 $X \subset {\mathbb {P}} H^{0} (X,L)$ is
$X \subset {\mathbb {P}} H^{0} (X,L)$ is 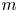 $m$-regular then
$m$-regular then 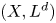 $(X,L^{d} )$ satisfies property
$(X,L^{d} )$ satisfies property  $\mathsf {QR}(3)$ for all
$\mathsf {QR}(3)$ for all 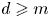 $d \geqslant m$, and (ii) if
$d \geqslant m$, and (ii) if 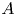 $A$ is an ample line bundle on
$A$ is an ample line bundle on 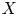 $X$ then
$X$ then 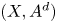 $(X,A^{d} )$ satisfies property
$(X,A^{d} )$ satisfies property 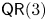 $\mathsf {QR}(3)$ for all sufficiently large even numbers
$\mathsf {QR}(3)$ for all sufficiently large even numbers 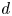 $d$. These results provide affirmative evidence for the expectation that property
$d$. These results provide affirmative evidence for the expectation that property 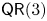 $\mathsf {QR}(3)$ holds for all sufficiently ample line bundles on
$\mathsf {QR}(3)$ holds for all sufficiently ample line bundles on 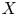 $X$, as in the cases of Green and Lazarsfeld's condition
$X$, as in the cases of Green and Lazarsfeld's condition 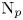 $\mathrm {N}_p$ and the Eisenbud–Koh–Stillman determininantal presentation in Eisenbud et al. [Determinantal equations for curves of high degree, Amer. J. Math. 110 (1988), 513–539]. Finally, when
$\mathrm {N}_p$ and the Eisenbud–Koh–Stillman determininantal presentation in Eisenbud et al. [Determinantal equations for curves of high degree, Amer. J. Math. 110 (1988), 513–539]. Finally, when 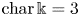 ${\rm char}\,\Bbbk = 3$ we prove that
${\rm char}\,\Bbbk = 3$ we prove that 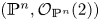 $({\mathbb {P}}^{n} , \mathcal {O}_{{\mathbb {P}}^{n}} (2))$ fails to satisfy property
$({\mathbb {P}}^{n} , \mathcal {O}_{{\mathbb {P}}^{n}} (2))$ fails to satisfy property 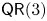 $\mathsf {QR}(3)$ for all
$\mathsf {QR}(3)$ for all 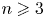 $n \geqslant 3$.
$n \geqslant 3$.
Information
- Type
- Research Article
- Information
- Copyright
- © 2021 The Author(s). The publishing rights in this article are licensed to Foundation Compositio Mathematica under an exclusive licence
References
- 7
- Cited by

