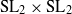Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
BHARGAVA, MANJUL
HO, WEI
and
KUMAR, ABHINAV
2016.
ORBIT PARAMETRIZATIONS FOR K3 SURFACES.
Forum of Mathematics, Sigma,
Vol. 4,
Issue. ,
Gotou, Rin
2023.
Dynamical systems of correspondences on the projective line I: Moduli spaces and multiplier maps.
Conformal Geometry and Dynamics of the American Mathematical Society,
Vol. 27,
Issue. 8,
p.
294.