Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-10T16:18:26.078Z Has data issue: false hasContentIssue false
  • English
  • Français

Refined curve counting with tropical geometry

Part of: Projective and enumerative geometry

Published online by Cambridge University Press:  18 August 2015

Florian Block  and
Lothar Göttsche
Florian Block
Affiliation:
Department of Mathematics, University of California, Berkeley, CA, USA email florian.s.block@gmail.com
Lothar Göttsche
Affiliation:
International Centre for Theoretical Physics, Strada Costiera 11, 34151 Trieste, Italy email gottsche@ictp.it
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

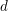The Severi degree is the degree of the Severi variety parametrizing plane curves of degree $d$ with 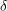${\it\delta}$ nodes. Recently, Göttsche and Shende gave two refinements of Severi degrees, polynomials in a variable 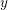$y$, which are conjecturally equal, for large 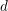$d$. At 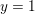$y=1$, one of the refinements, the relative Severi degree, specializes to the (non-relative) Severi degree. We give a tropical description of the refined Severi degrees, in terms of a refined tropical curve count for all toric surfaces. We also refine the equivalent count of floor diagrams for Hirzebruch and rational ruled surfaces. Our description implies that, for fixed 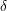${\it\delta}$, the refined Severi degrees are polynomials in 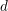$d$ and 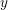$y$, for large 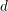$d$. As a consequence, we show that, for 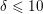${\it\delta}\leqslant 10$ and all 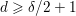$d\geqslant {\it\delta}/2+1$, both refinements of Göttsche and Shende agree and equal our refined counts of tropical curves and floor diagrams.

Keywords

Severi varietyrefined Severi degreeGöttsche conjectureWelschinger invarianttropical geometryfloor diagram

MSC classification

Primary: 14N10: Enumerative problems (combinatorial problems)
Secondary: 14N35: Gromov-Witten invariants, quantum cohomology, Gopakumar-Vafa invariants, Donaldson-Thomas invariants 14T05: Tropical geometry
Type
Research Article
Information
Compositio Mathematica , Volume 152 , Issue 1 , January 2016 , pp. 115 - 151
Copyright
© The Authors 2015 

References

Ardila, F. and Block, F., Universal polynomials for Severi degrees of toric surfaces, Adv. Math. 237 (2013), 165–193.CrossRefGoogle Scholar
Bernstein, D. N., The number of roots of a system of equations, Funktsional. Anal. i Prilozhen. 9 (1975), 1–4.Google Scholar
Block, F., Computing node polynomials for plane curves, Math. Res. Lett. 18 (2011), 621–643.CrossRefGoogle Scholar
Block, F., Relative node polynomials for plane curves, J. Algebraic Combin. 36 (2012), 279–308.CrossRefGoogle Scholar
Brugallé, E., Personal communication (2013).Google Scholar
Brugallé, E. and Mikhalkin, G., Enumeration of curves via floor diagrams, C. R. Math. Acad. Sci. Paris 345 (2007), 329–334.CrossRefGoogle Scholar
Brugallé, E. and Mikhalkin, G., Floor decompositions of tropical curves: the planar case, in Proc. Gökova Geometry–Topology Conf., Gökova, 2008 (Gökova Geometry–Topology Conferences, Gökova, 2009), 64–90.Google Scholar
Caporaso, L. and Harris, J., Counting plane curves of any genus, Invent. Math. 131 (1998), 345–392.CrossRefGoogle Scholar
Di Francesco, P. and Itzykson, C., Quantum intersection rings, in The moduli space of curves (Texel Island, 1994), Progress in Mathematics, vol. 129 (Birkhäuser, Boston, MA, 1995), 81–148.CrossRefGoogle Scholar
Fomin, S. and Mikhalkin, G., Labeled floor diagrams for plane curves, J. Eur. Math. Soc. (JEMS) 12 (2010), 1453–1496.Google Scholar
Gathmann, A. and Markwig, H., The Caporaso–Harris formula and plane relative Gromov-Witten invariants in tropical geometry, Math. Ann. 338 (2007), 845–868.CrossRefGoogle Scholar
Getzler, E., Intersection theory on M1, 4 and elliptic Gromov–Witten invariants, J. Amer. Math. Soc. 10 (1997), 973–998.CrossRefGoogle Scholar
Göttsche, L., A conjectural generating function for numbers of curves on surfaces, Comm. Math. Phys. 196 (1998), 523–533.Google Scholar
Göttsche, L. and Shende, V., The ${\it\chi}_{-y}$genera of relative Hilbert schemes for linear systems on Abelian and K3 surfaces, Algebraic Geometry, to appear, arXiv:1307.4316 [math.AG].Google Scholar
Göttsche, L. and Shende, V., Refined curve counting on complex surfaces, Geom. Topol. 18 (2014), 2245–2307.CrossRefGoogle Scholar
Itenberg, I., Kharlamov, V. and Shustin, E., A Caporaso-Harris type formula for Welschinger invariants of real toric del Pezzo surfaces, Comment. Math. Helv. 84 (2009), 87–126.CrossRefGoogle Scholar
Itenberg, I. and Mikhalkin, G., On Block-Göttsche multiplicities for planar tropical curves, Int. Math. Res. Not. IMRN 2013 (2013), 5289–5320.CrossRefGoogle Scholar
Kleiman, S. L. and Shende, V., On the Göttsche Threshold, in A celebration of algebraic geometry, Clay Mathematics Proceedings, vol. 18 (American Mathematical Society, Providence, RI, 2013), 429–449; with an appendix by Ilya Tyomkin.Google Scholar
Kool, M., Shende, V. and Thomas, R. P., A short proof of the Göttsche conjecture, Geom. Topol. 15 (2011), 397–406.CrossRefGoogle Scholar
Mikhalkin, G., Enumerative tropical geometry in ℝ2, J. Amer. Math. Soc. 18 (2005), 313–377.CrossRefGoogle Scholar
Pandharipande, R. and Thomas, R. P., Stable pairs and BPS invariants, J. Amer. Math. Soc. 23 (2010), 267–297.CrossRefGoogle Scholar
Ran, Z., Enumerative geometry of singular plane curves, Invent. Math. 97 (1989), 447–469.CrossRefGoogle Scholar
Sagan, B. E., The cyclic sieving phenomenon: a survey, in Surveys in combinatorics 2011, London Mathematical Society Lecture Note Series, vol. 392 (Cambridge University Press, Cambridge, 2011), 183–233; MR 2866734.CrossRefGoogle Scholar
Shustin, E., A tropical approach to enumerative geometry, Algebra i Analiz 17 (2005), 170–214.Google Scholar
Steiner, J., Elementare Lösung einer geometrischen Aufgabe, und über einige damit in Beziehung stehende Eigenschaften der Kegelschnitte, J. Reine Angew. Math. 37 (1848), 161–192.Google Scholar
Tzeng, Y.-J., A proof of Göttsche-Yau-Zaslow formula, J. Differential Geom. 90 (2012), 439–472.CrossRefGoogle Scholar
Vakil, R., Counting curves on rational surfaces, Manuscripta Math. 102 (2000), 53–84.CrossRefGoogle Scholar