Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-13T06:53:26.819Z Has data issue: false hasContentIssue false
  • English
  • Français

Relation between two twisted inverse image pseudofunctors in duality theory

Part of: Commutative algebra: Homological methods (Co)homology theory

Published online by Cambridge University Press:  19 November 2014

Srikanth B. Iyengar ,
Joseph Lipman  and
Amnon Neeman
Srikanth B. Iyengar
Affiliation:
Department of Mathematics, University of Nebraska, Lincoln, NE 68588, USA email s.b.iyengar@unl.edu
Joseph Lipman
Affiliation:
Department of Mathematics, Purdue University, West Lafayette, IN 47907, USA email jlipman@purdue.edu
Amnon Neeman
Affiliation:
Centre for Mathematics and its Applications, Mathematical Sciences Institute Australian National University, Canberra, ACT 0200, Australia email Amnon.Neeman@anu.edu.au
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Grothendieck duality theory assigns to essentially finite-type maps 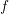$f$ of noetherian schemes a pseudofunctor 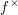$f^{\times }$ right-adjoint to 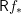$\mathsf{R}f_{\ast }$, and a pseudofunctor 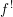$f^{!}$ agreeing with 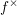$f^{\times }$ when 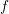$f$ is proper, but equal to the usual inverse image 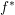$f^{\ast }$ when 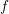$f$ is étale. We define and study a canonical map from the first pseudofunctor to the second. This map behaves well with respect to flat base change, and is taken to an isomorphism by ‘compactly supported’ versions of standard derived functors. Concrete realizations are described, for instance for maps of affine schemes. Applications include proofs of reduction theorems for Hochschild homology and cohomology, and of a remarkable formula for the fundamental class of a flat map of affine schemes.

Keywords

Grothendieck dualitytwisted inverse image pseudofunctorsHochschild derived functorsrelative perfectionrelative dualizing complexfundamental class

MSC classification

Primary: 14F05: Sheaves, derived categories of sheaves and related constructions 13D09: Derived categories
Secondary: 13D03: (Co)homology of commutative rings and algebras (e.g., Hochschild, André-Quillen, cyclic, dihedral, etc.)
Type
Research Article
Information
Compositio Mathematica , Volume 151 , Issue 4 , April 2015 , pp. 735 - 764
Copyright
© The Author(s) 2014 

References

Avramov, L. L., Iyengar, S. B. and Lipman, J., Reflexivity and rigidity for complexes, II: Schemes, Algebra Number Theory 5 (2011), 379–429.Google Scholar
Avramov, L. L., Iyengar, S. B., Lipman, J. and Nayak, S., Reduction of derived Hochschild functors over commutative algebras and schemes, Adv. Math. 223 (2010), 735–772.Google Scholar
Alonso Tarrío, L., Jeremías López, A. and Lipman, J., Local homology and cohomology on schemes, Ann. Sci. Éc. Norm. Supér. 30 (1997), 1–39.Google Scholar
Alonso Tarrío, L., Jeremías López, A. and Lipman, J., Duality and flat base change on formal schemes, Contemporary Mathematics, vol. 244 (American Mathematical Society, Providence, RI, 1999), 3–90.Google Scholar
Alonso Tarrío, L., Jeremías López, A. and Lipman, J., Bivariance, Grothendieck duality and Hochschild homology I: Construction of a bivariant theory, Asian J. Math. 15 (2011), 451–497.Google Scholar
Alonso Tarrío, L., Jeremías López, A. and Lipman, J., Bivariance, Grothendieck duality and Hochschild homology II: the fundamental class of a flat scheme-map, Adv. Math. 257 (2014), 365–461.Google Scholar
Alonso Tarrío, L., Jeremías López, A. and Souto Salorio, M. J., Bousfield localization on formal schemes, J. Algebra 278 (2004), 585–610.CrossRefGoogle Scholar
Bökstedt, M. and Neeman, A., Homotopy limits in triangulated categories, Compositio Math. 86 (1993), 209–234.Google Scholar
Dwyer, W. G. and Greenlees, J. P. C., Complete modules and torsion modules, Amer. J. Math. 124 (2002), 199–220.Google Scholar
Dwyer, W. G., Greenlees, J. P. C. and Iyengar, S. B., Finiteness in derived categories of local rings, Comment. Math. Helv. 81 (2006), 383–432.Google Scholar
Foxby, H. B., Bounded complexes of flat modules, J. Pure Appl. Algebra 15 (1979), 149–172.Google Scholar
Foxby, H. B. and Iyengar, S. B., Depth and amplitude for unbounded complexes, in Commutative algebra and its interaction with algebraic geometry (Grenoble–Lyon, 2001), Contemporary Mathematics, vol. 331 (American Mathematical Society, Providence, RI, 2003), 119–137.Google Scholar
Grothendieck, A., Formule de Lefschetz, in Cohomologie l-adique et Fonctions L (SGA 5), Lecture Notes in Mathematics, vol. 589 (Springer, New York, 1971), 73–137.Google Scholar
Grothendieck, A. and Dieudonné, J., Eléments de Géométrie Algébrique II, Étude gobale élémentaire de quelques classes de morphisme, Publications Mathématiques, vol. 8 (Institut des Hautes Études Scientifiques, Paris, 1961).Google Scholar
Grothendieck, A. and Dieudonné, J., Eléments de Géométrie Algébrique IV, Étude locale des schémas et des morphismes of schémas, Publications Mathématiques, vols. 28 and 32 (Institut des Hautes Études Scientifiques, Paris, 1966/67).Google Scholar
Hartshorne, R., Residues and duality, Lecture Notes in Mathematics, vol. 20 (Springer, New York, 1966).Google Scholar
Hübl, R. and Kunz, E., Integration of differential forms on schemes, J. Reine Angew. Math. 410 (1990), 53–83.Google Scholar
Hübl, R. and Kunz, E., Regular differential forms and duality for projective morphisms, J. Reine Angew. Math. 410 (1990), 84–108.Google Scholar
Illusie, L., Conditions de finitude relative, in Théorie des Intersections et Théorème de Riemann–Roch (SGA 6), Lecture Notes in Mathematics, vol. 225 (Springer, New York, 1971), 222–273.Google Scholar
Lipman, J., Notes on derived categories and Grothendieck Duality, in Foundations of Grothendieck duality for diagrams of schemes, Lecture Notes in Mathematics, vol. 1960 (Springer, New York, 2009), 1–259.Google Scholar
Nayak, S., Compactification for essentially finite type maps, Adv. Math. 222 (2009), 527–546.Google Scholar
Neeman, A., The chromatic tower for D(R), Topology 31 (1992), 519–532.Google Scholar
Neeman, A., The Grothendieck duality theorem via Bousfield’s techniques and Brown representability, J. Amer. Math. Soc. 9 (1996), 205–236.Google Scholar
Neeman, A., The decomposition of $\text{Hom}_{k}(S,k)$into indecomposable injectives, Acta Math. Vietnam., to appear.Google Scholar
Neeman, A., An improvement on the base-change theorem and the functor $f^{!}$, Preprint (2014), arXiv:1406.7599.Google Scholar
Sastry, P., Base change and Grothendieck duality for Cohen-Macaulay maps, Compositio Math. 140 (2004), 729–777.CrossRefGoogle Scholar
Thomason, R., The classification of triangulated subcategories, Compositio Math. 105 (1997), 1–27.CrossRefGoogle Scholar