Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-10T12:39:11.880Z Has data issue: false hasContentIssue false
  • English
  • Français

Restrictions on the prime-to-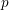$p$ fundamental group of a smooth projective variety

Part of: Curves

Published online by Cambridge University Press:  06 March 2015

Donu Arapura
Donu Arapura*
Affiliation:
Department of Mathematics, Purdue University, West Lafayette, IN 47907, USA email dvb@math.purdue.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The goal of this paper is to obtain restrictions on the prime-to-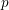$p$ quotient of the étale fundamental group of a smooth projective variety in characteristic 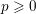$p\geqslant 0$. The results are analogues of some theorems from the study of Kähler groups. Our first main result is that such groups are indecomposable under coproduct. The second result gives a classification of the pro-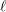$\ell$ parts of one-relator groups in this class.

Keywords

fundamental groupprojective variety

MSC classification

Primary: 14H30: Coverings, fundamental group
Type
Research Article
Information
Compositio Mathematica , Volume 151 , Issue 6 , June 2015 , pp. 1083 - 1095
Copyright
© The Author 2015 

References

Arapura, D., Bressler, P. and Ramachandran, M., On the fundamental group of a compact Kähler manifold, Duke Math. J. 68 (1992), 477–488.CrossRefGoogle Scholar
Arapura, D., Fundamental groups of smooth projective varieties, in Current topics in complex algebraic geometry, vol. 28 (Cambridge University Press, Cambridge, 1995), 1–16.Google Scholar
Biswas, I. and Mahan, M. J., One-relator Kähler groups, Geom. Topol. 16 (2012), 2171–2186.CrossRefGoogle Scholar
Deligne, P., Théorie de Hodge III, Publ. Math. Inst. Hautes Études Sci. 44 (1974), 5–7.CrossRefGoogle Scholar
Deligne, P., La conjecture de Weil II, Publ. Math. Inst. Hautes Études Sci. 52 (1980), 137–252.CrossRefGoogle Scholar
Demushkin, S., On the maximal p-extension of a local field, Izv. Akad. Nauk USSR Math. Ser. 25 (1961), 329–346.Google Scholar
Gromov, M., Sur le groupe fondamental d’une variete kählerienne, C. R. Acad. Sci. Paris 308 (1989), 67–70.Google Scholar
Grothendieck, A., Sur quelques points d’algebre homologique, Tohoku Math. J. 9 (1957), 119–221.Google Scholar
Jannsen, U., Continuous étale cohomology, Math. Ann. 280 (1988), 207–245.CrossRefGoogle Scholar
Johnson, F. and Rees, E., On the fundamental group of a complex algebraic manifold, Bull. Lond. Math. Soc. 19 (1987), 463–466.CrossRefGoogle Scholar
Kotschick, D., The deficiencies of Kähler groups, J. Topol. 5 (2012), 639–650.CrossRefGoogle Scholar
Labute, J., Classification of Demushkin groups, J. Canad. Math. Soc. 19 (1967), 106–132.CrossRefGoogle Scholar
Lazard, M., Sur les groupes des nilpotents and anneaux de Lie, Ann. Sci. Éc. Norm. Supér. 71 (1954), 101–190.CrossRefGoogle Scholar
Lieblich, M. and Olsson, M., Generators and relations for the étale fundamental group, Pure Appl. Math. Q. 6 (2010), 209–243.CrossRefGoogle Scholar
Milne, J., Étale cohomology (Princeton University Press, Princeton, NJ, 1980).Google Scholar
Milne, J., Abelian varieties, in Arithmetic geometry (Storrs, Conn., 1984) (Springer, New York, 1986), 103–150.CrossRefGoogle Scholar
Reznikov, A., The structure of Kähler groups. I. Second cohomology, in Motives, polylogarithms and Hodge theory, International Press Lecture Series, vol. 3, II (International Press, Boston, 2002), 717–730.Google Scholar
Ribes, L. and Zaleskii, P., Profinite groups, second edition (Springer, Berlin, 2010).CrossRefGoogle Scholar
Serre, J. P., Cohomologie galoisienne, Lecture Notes in Mathematics, vol. 5 (Springer, Berlin, 1965).CrossRefGoogle Scholar
Serre, J. P., Trees (Springer, Berlin, 2003).Google Scholar
Grothendieck, A. et al. , Séminaire de Géométrie Algébrique du Bois Marie – 1960–61 – Revêtements étale et groupe fondamental (SGA1), Lecture Notes in Mathematics, vol. 224 (Springer, Berlin, 1971).Google Scholar
Raynaud, M., Propriétés de finitude de groupe fondamental, in Séminaire de Géométrie Algébrique du Bois Marie – 1967–69 – Groupes de monodromie en géométrie algébrique (SGA7), Lecture Notes in Mathematics, vol. 288 (Springer, Berlin, 1972); Exposé II.Google Scholar
Stallings, J., Homology and central series of groups, J. Algebra 2 (1965), 170–181.CrossRefGoogle Scholar