Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-10T17:38:37.316Z Has data issue: false hasContentIssue false
  • English
  • Français

Smoothing Calabi–Yau toric hypersurfaces using the Gross–Siebert algorithm

Part of: Special varieties Surfaces and higher-dimensional varieties

Published online by Cambridge University Press:  17 June 2021

Thomas Prince
Thomas Prince*
Affiliation:
The Abbey School, Kendrick Road, ReadingRG1 5DZ, UKprinceth@theabbey.co.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

We explain how to form a novel dataset of Calabi–Yau threefolds via the Gross–Siebert algorithm. We expect these to degenerate to Calabi–Yau toric hypersurfaces with certain Gorenstein (not necessarily isolated) singularities. In particular, we explain how to ‘smooth the boundary’ of a class of four-dimensional reflexive polytopes to obtain polarised tropical manifolds. We compute topological invariants of a compactified torus fibration over each such tropical manifold, expected to be homeomorphic to the general fibre of the Gross–Siebert smoothing. We consider a family of examples related to products of reflexive polygons. Among these we find 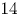$14$ topological types with $b_2=1$ that do not appear in existing lists of known rank-one Calabi–Yau threefolds.

Keywords

Calabi–Yau manifoldstoric degenerations

MSC classification

Primary: 14J32: Calabi-Yau manifolds
Secondary: 14J33: Mirror symmetry 14M25: Toric varieties, Newton polyhedra 14J81: Relationships with physics
Type
Research Article
Information
Compositio Mathematica , Volume 157 , Issue 7 , July 2021 , pp. 1441 - 1491
Check for updates
Copyright
© The Author(s) 2021

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Almkvist, G., van Enckevort, C., van Straten, D. and Zudilin, W., Tables of Calabi–Yau equations, Preprint (2005), arXiv:math/0507430 [math.AG].Google Scholar
Almkvist, G. and Zudilin, W., Differential equations, mirror maps and zeta values, in Mirror symmetry. V, AMS/IP Studies in Advanced Mathematics, vol. 38 (American Mathematical Society, Providence, RI, 2006), 481–515.Google Scholar
Altmann, K., The versal deformation of an isolated toric Gorenstein singularity, Invent. Math. 128 (1997), 443–479.CrossRefGoogle Scholar
Argüz, H., Real loci in (log-) Calabi–Yau manifolds via Kato–Nakayama spaces of toric degenerations, Preprint (2016), arXiv:1610.07195 [math.AG].Google Scholar
Artin, M., On the solutions of analytic equations, Invent. Math. 5 (1968), 277–291.CrossRefGoogle Scholar
Aspinwall, P. S., Bridgeland, T., Craw, A., Douglas, M. R., Kapustin, A., Moore, G. W., Gross, M., Segal, G., Szendröi, B. and Wilson, P. M. H., Dirichlet branes and mirror symmetry, Clay Mathematics Monographs, vol. 4 (American Mathematical Society, Providence, RI, 2009).Google Scholar
Batyrev, V. V., Dual polyhedra and mirror symmetry for Calabi-Yau hypersurfaces in toric varieties, J. Algebraic Geom. 3 (1994), 493–535.Google Scholar
Batyrev, V. V. and Borisov, L. A., On Calabi-Yau complete intersections in toric varieties, in Higher-dimensional complex varieties (Trento, 1994) (de Gruyter, Berlin, 1996), 39–65.Google Scholar
Batyrev, V. and Kreuzer, M., Integral cohomology and mirror symmetry for Calabi-Yau 3-folds, in Mirror symmetry. V, AMS/IP Studies in Advanced Mathematics, vol. 38 (American Mathematical Society, Providence, RI, 2006), 255–270.Google Scholar
Batyrev, V. and Kreuzer, M., Constructing new Calabi-Yau 3-folds and their mirrors via conifold transitions, Adv. Theor. Math. Phys. 14 (2010), 879–898.CrossRefGoogle Scholar
Bosma, W., Cannon, J. and Playoust, C., The Magma algebra system. I. The user language, J. Symbolic Comput. 24 (1997), 235–265.CrossRefGoogle Scholar
Brown, G., Kerber, M. and Reid, M., Fano 3-folds in codimension 4, Tom and Jerry. Part I, Compos. Math. 148 (2012), 1171–1194.CrossRefGoogle Scholar
Candelas, P., Constantin, A. and Mishra, C., Calabi-Yau threefolds with small Hodge numbers, Fortschr. Phys. 66 (2018), 1800029.CrossRefGoogle Scholar
Candelas, P., Lütken, C. A. and Schimmrigk, R., Complete intersection Calabi-Yau manifolds. II. Three generation manifolds, in Proceedings of the Fourth Seminar on Quantum Gravity (Moscow, 1987) (World Scientific Publishing, Teaneck, NJ, 1988), 435–468.Google Scholar
Candelas, P., Lynker, M. and Schimmrigk, R., Calabi-Yau manifolds in weighted $\textbf {P}_4$, Nuclear Phys. B 341 (1990), 383–402.CrossRefGoogle Scholar
Castano Bernard, R. and Matessi, D., Lagrangian 3-torus fibrations, J. Differential Geom. 81 (2009), 483–573.CrossRefGoogle Scholar
Coates, T., Corti, A., Galkin, S., Golyshev, V. and Kasprzyk, A. M., Mirror symmetry and Fano manifolds, in European Congress of Mathematics Kraków, 2–7 July, 2012 (European Mathematical Society, Zürich, 2014), 285–300.Google Scholar
Cox, D. A., Little, J. B. and Schenck, H. K., Toric varieties, Graduate Studies in Mathematics, vol. 124 (American Mathematical Society, Providence, RI, 2011).CrossRefGoogle Scholar
Doran, C. F. and Morgan, J. W., Algebraic topology of Calabi-Yau threefolds in toric varieties, Geom. Topol. 11 (2007), 597–642.CrossRefGoogle Scholar
Felten, S., Filip, M. and Ruddat, H., Smoothing toroidal crossing spaces, Preprint (2019), arXiv:1908.11235 [math.AG].Google Scholar
Friedman, R., On threefolds with trivial canonical bundle, in Complex geometry and Lie theory (Sundance, UT, 1989), Proceedings of Symposia in Pure Mathematics, vol. 53 (American Mathematical Society, Providence, RI, 1991), 103–134.CrossRefGoogle Scholar
Galkin, S., Joins and Hadamard products. Talk at Steklov Mathematical Institute, during the conference ‘Categorical and Analytic Invariants in Algebraic Geometry’ (2015), http://www.mathnet.ru/eng/present12324.Google Scholar
Gross, M., Examples of special Lagrangian fibrations, in Symplectic geometry and mirror symmetry (Seoul, 2000) (World Scientific Publishing, River Edge, NJ, 2001), 81–109.CrossRefGoogle Scholar
Gross, M., Special Lagrangian fibrations. I. Topology [MR1672120 (2000e:14066)], in Winter School on Mirror Symmetry, Vector Bundles and Lagrangian Submanifolds (Cambridge, MA, 1999), AMS/IP Studies in Advanced Mathematics, vol. 23 (American Mathematical Society, Providence, RI, 2001), 65–93.Google Scholar
Gross, M., Topological mirror symmetry, Invent. Math. 144 (2001), 75–137.CrossRefGoogle Scholar
Gross, M., Toric degenerations and Batyrev-Borisov duality, Math. Ann. 333 (2005), 645–688.CrossRefGoogle Scholar
Gross, M. and Siebert, B., Mirror symmetry via logarithmic degeneration data. I, J. Differential Geom. 72 (2006), 169–338.CrossRefGoogle Scholar
Gross, M. and Siebert, B., Mirror symmetry via logarithmic degeneration data, II, J. Algebraic Geom. 19 (2010), 679–780.CrossRefGoogle Scholar
Gross, M. and Siebert, B., From real affine geometry to complex geometry, Ann. of Math. (2) 174 (2011), 1301–1428.CrossRefGoogle Scholar
Haase, C. and Zharkov, I., Integral affine structures on spheres: complete intersections, Int. Math. Res. Not. 2005 (2005), 3153–3167.CrossRefGoogle Scholar
Inoue, D., Calabi–Yau 3-folds from projective joins of del Pezzo manifolds, Preprint (2019), arXiv:1902.10040 [math.AG].Google Scholar
Kapustka, G., Projections of del Pezzo surfaces and Calabi-Yau threefolds, Adv. Geom. 15 (2015), 143–158.CrossRefGoogle Scholar
Knapp, J. and Sharpe, E., GLSMs, joins, and nonperturbatively-realized geometries, J. High Energy Phys. 64 (2019), 096.CrossRefGoogle Scholar
Kontsevich, M. and Soibelman, Y., Affine structures and non-Archimedean analytic spaces, in The unity of mathematics, Progress in Mathematics, vol. 244 (Birkhäuser, Boston, 2006), 321–385.Google Scholar
Kreuzer, M. and Skarke, H., Complete classification of reflexive polyhedra in four dimensions, Adv. Theor. Math. Phys. 4 (2000), 1209–1230.CrossRefGoogle Scholar
Lee, N.-H., Calabi-Yau threefolds with small $h^{1,1}$'s from Fano threefolds, Nuclear Phys. B 922 (2017), 384–400.CrossRefGoogle Scholar
Lee, N.-H., d-Semistable Calabi–Yau threefolds of type III, Manuscripta Math. 12 (2018), 257–281.Google Scholar
Libgober, A. and Teitelbaum, J., Lines on Calabi-Yau complete intersections, mirror symmetry, and Picard-Fuchs equations, Int. Math. Res. Not. 1993 (1993), 29–39.CrossRefGoogle Scholar
Nakayama, C. and Ogus, A., Relative rounding in toric and logarithmic geometry, Geom. Topol. 14 (2010), 2189–2241.CrossRefGoogle Scholar
Nill, B. and Ziegler, G. M., Projecting lattice polytopes without interior lattice points, Math. Oper. Res. 36 (2011), 462–467.CrossRefGoogle Scholar
Prince, T., Lagrangian torus fibration models of Fano threefolds, Preprint (2018), arXiv:1801.02997 [math.GT].Google Scholar
Prince, T., Calabi–Yau threefolds via the Gross–Siebert algorithm, Preprint (2019), https://github.com/T-Prince/Calabi-Yau-threefolds-via-the-Gross-Siebert-algorithm.Google Scholar
Ruan, W.-D., Generalized special Lagrangian torus fibration for Calabi-Yau hypersurfaces in toric varieties. I, Commun. Contemp. Math. 9 (2007), 201–216.CrossRefGoogle Scholar
Ruddat, H., Log Hodge groups on a toric Calabi-Yau degeneration, in Mirror symmetry and tropical geometry, Contemporary Mathematics, vol. 527 (American Mathematical Society, Providence, RI, 2010), 113–164.CrossRefGoogle Scholar
Ruddat, H. and Siebert, B., Period integrals from wall structures via tropical cycles, canonical coordinates in mirror symmetry and analyticity of toric degenerations, Publ. Math. Inst. Hautes Études Sci. 132 (2020), 1–82.CrossRefGoogle Scholar
Ruddat, H. and Zharkov, I., Compactifying torus fibrations over integral affine manifolds with singularities, Preprint (2020), arXiv:2003.08521 [math.AG].CrossRefGoogle Scholar
Tian, G., Smoothing 3-folds with trivial canonical bundle and ordinary double points, in Essays on mirror manifolds (International Press, Hong Kong, 1992), 458–479.Google Scholar
van Enckevort, C. and van Straten, D., Monodromy calculations of fourth order equations of Calabi-Yau type, in Mirror symmetry.V, AMS/IP Studies in Advanced Mathematics, vol. 38 (American Mathematical Society, Providence, RI, 2006), 539–559.Google Scholar
van Straten, D., Calabi-Yau operators database, http://www.mathematik.uni-mainz.de/CYequations/db/.Google Scholar