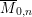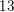Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Doran, Brent
Giansiracusa, Noah
and
David, Jensen
2017.
A simplicial approach to effective divisors in M¯0,n.
International Mathematics Research Notices,
Vol. 2017,
Issue. 2,
p.
529.
Mullane, Scott
2017.
On the effective cone of M‾g,n.
Advances in Mathematics,
Vol. 320,
Issue. ,
p.
500.
Hausen, Jürgen
Keicher, Simon
and
Laface, Antonio
2018.
On blowing up the weighted projective plane.
Mathematische Zeitschrift,
Vol. 290,
Issue. 3-4,
p.
1339.
Chen, Dawei
2018.
Geometry of Moduli.
Vol. 14,
Issue. ,
p.
65.
González Anaya, Javier
González, José Luis
and
Karu, Kalle
2019.
Constructing non-Mori Dream Spaces from negative curves.
Journal of Algebra,
Vol. 539,
Issue. ,
p.
118.
Sannai, Akiyoshi
and
Tanaka, Hiromu
2019.
Infinitely generated symbolic Rees algebras over finite fields .
Algebra & Number Theory,
Vol. 13,
Issue. 8,
p.
1879.
Moon, Han-Bom
and
Swinarski, David
2019.
On the S-invariant F-conjecture.
Journal of Algebra,
Vol. 517,
Issue. ,
p.
439.
He, Zhuang
2019.
Mori Dream Spaces and blow-ups of weighted projective spaces.
Journal of Pure and Applied Algebra,
Vol. 223,
Issue. 10,
p.
4426.
Dumitrescu, Olivia
and
Postinghel, Elisa
2019.
Positivity of divisors on blown-up projective spaces, II.
Journal of Algebra,
Vol. 529,
Issue. ,
p.
226.
HAUSEN, JÜRGEN
HISCHE, CHRISTOFF
and
WROBEL, MILENA
2019.
ON TORUS ACTIONS OF HIGHER COMPLEXITY.
Forum of Mathematics, Sigma,
Vol. 7,
Issue. ,
González, José Luis
and
Karu, Kalle
2019.
Examples of Non-finitely Generated Cox Rings.
Canadian Mathematical Bulletin,
Vol. 62,
Issue. 02,
p.
267.
González Anaya, Javier
González, José Luis
and
Karu, Kalle
2019.
On a family of negative curves.
Journal of Pure and Applied Algebra,
Vol. 223,
Issue. 11,
p.
4871.
Kurano, Kazuhiko
and
Nishida, Koji
2019.
Infinitely Generated Symbolic Rees Rings of Space Monomial Curves Having Negative Curves.
Michigan Mathematical Journal,
Vol. 68,
Issue. 2,
Laface, Antonio
and
Ugaglia, Luca
2020.
Cox ring of the generic fiber.
Journal of Algebra,
Vol. 551,
Issue. ,
p.
191.
González, José Luis
Gunther, Elijah
and
Zhang, Olivia
2020.
Balanced complexes and effective divisors on M¯0,n.
Communications in Algebra,
Vol. 48,
Issue. 6,
p.
2662.
Laface, Antonio
and
Ugaglia, Luca
2020.
On base loci of higher fundamental forms of toric varieties.
Journal of Pure and Applied Algebra,
Vol. 224,
Issue. 12,
p.
106447.
Eur, Christopher
2020.
Divisors on matroids and their volumes.
Journal of Combinatorial Theory, Series A,
Vol. 169,
Issue. ,
p.
105135.
Mullane, Scott
2021.
Non-polyhedral effective cones from the moduli space of curves.
Transactions of the American Mathematical Society,
Vol. 374,
Issue. 9,
p.
6397.
He, Zhuang
and
Yang, Lei
2021.
Birational Geometry of Blow-ups of Projective Spaces Along Points and Lines.
International Mathematics Research Notices,
Vol. 2021,
Issue. 9,
p.
6442.
Grifo, Eloísa
and
Seceleanu, Alexandra
2021.
Commutative Algebra.
p.
343.