Article contents
Spinor groups with good reduction
Published online by Cambridge University Press: 07 March 2019
Abstract
Let 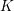 $K$ be a two-dimensional global field of characteristic
$K$ be a two-dimensional global field of characteristic 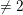 $\neq 2$ and let
$\neq 2$ and let 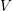 $V$ be a divisorial set of places of
$V$ be a divisorial set of places of 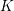 $K$. We show that for a given
$K$. We show that for a given 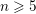 $n\geqslant 5$, the set of
$n\geqslant 5$, the set of 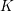 $K$-isomorphism classes of spinor groups
$K$-isomorphism classes of spinor groups 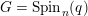 $G=\operatorname{Spin}_{n}(q)$ of nondegenerate
$G=\operatorname{Spin}_{n}(q)$ of nondegenerate  $n$-dimensional quadratic forms over
$n$-dimensional quadratic forms over 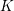 $K$ that have good reduction at all
$K$ that have good reduction at all 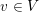 $v\in V$ is finite. This result yields some other finiteness properties, such as the finiteness of the genus
$v\in V$ is finite. This result yields some other finiteness properties, such as the finiteness of the genus 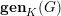 $\mathbf{gen}_{K}(G)$ and the properness of the global-to-local map in Galois cohomology. The proof relies on the finiteness of the unramified cohomology groups
$\mathbf{gen}_{K}(G)$ and the properness of the global-to-local map in Galois cohomology. The proof relies on the finiteness of the unramified cohomology groups 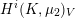 $H^{i}(K,\unicode[STIX]{x1D707}_{2})_{V}$ for
$H^{i}(K,\unicode[STIX]{x1D707}_{2})_{V}$ for 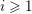 $i\geqslant 1$ established in the paper. The results for spinor groups are then extended to some unitary groups and to groups of type
$i\geqslant 1$ established in the paper. The results for spinor groups are then extended to some unitary groups and to groups of type 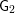 $\mathsf{G}_{2}$.
$\mathsf{G}_{2}$.
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- © The Authors 2019
Footnotes
The first author was supported by the Canada Research Chairs Program and by an NSERC research grant. The second author was partially supported by the Simons Foundation. During the preparation of the final version of the paper, he visited Princeton University and the Institute for Advanced Study, and would like to thankfully acknowledge the hospitality of both institutions. The third author was partially supported by an AMS-Simons Travel Grant. We are grateful to P. Gille and M. Rapoport for useful conversations. Last but not least, we would like to express our gratitude to all anonymous referees whose comments, insights and suggestions helped to improve the original paper significantly.
References
- 8
- Cited by

