Hostname: page-component-68c7f8b79f-kpv4p Total loading time: 0 Render date: 2025-12-18T18:38:19.373Z Has data issue: false hasContentIssue false
  • English
  • Français

Stability in the high-dimensional cohomology of congruence subgroups

Part of: Whitehead groups and $K_1$ Rings and algebras arising under various constructions Other groups of matrices Discontinuous groups and automorphic forms Homology and cohomology theories

Published online by Cambridge University Press:  24 March 2020

Jeremy Miller ,
Rohit Nagpal  and
Peter Patzt
Jeremy Miller
Affiliation:
Department of Mathematics, Purdue University, 150 North University Street, West Lafayette, IN 47904, USA email jeremykmiller@purdue.edu
Rohit Nagpal
Affiliation:
Department of Mathematics, University of Michigan, 530 Church Street, Ann Arbor, MI 48109, USA email rohitna@umich.edu
Peter Patzt
Affiliation:
Department of Mathematics, Purdue University, 150 North University Street, West Lafayette, IN 47904, USA email ppatzt@purdue.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove a representation stability result for the codimension-one cohomology of the level-three congruence subgroup of 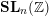$\mathbf{SL}_{n}(\mathbb{Z})$. This is a special case of a question of Church, Farb, and Putman which we make more precise. Our methods involve proving finiteness properties of the Steinberg module for the group 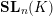$\mathbf{SL}_{n}(K)$ for 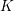$K$ a field. This also lets us give a new proof of Ash, Putman, and Sam’s homological vanishing theorem for the Steinberg module. We also prove an integral refinement of Church and Putman’s homological vanishing theorem for the Steinberg module for the group 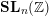$\mathbf{SL}_{n}(\mathbb{Z})$.

Keywords

congruence subgroupsKoszul algebrasrepresentation stabilityBorel–Serre duality

MSC classification

Primary: 11F75: Cohomology of arithmetic groups 55N25: Homology with local coefficients, equivariant cohomology 20H05: Unimodular groups, congruence subgroups 19B14: Stability for linear groups 16S37: Quadratic and Koszul algebras

Information

Type
Research Article
Information
Compositio Mathematica , Volume 156 , Issue 4 , April 2020 , pp. 822 - 861
Copyright
© The Authors 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

Jeremy Miller was supported in part by NSF grant DMS-1709726.

References

Ash, A., Unstable cohomology of SL (n, O), J. Algebra 167 (1994), 330–342; MR 1283290.CrossRefGoogle Scholar
Ash, A., Gunnells, P. E. and McConnell, M., Cohomology of congruence subgroups of SL4(ℤ), J. Number Theory 94 (2002), 181–212; MR 1904968.CrossRefGoogle Scholar
Ash, A., Gunnells, P. E. and McConnell, M., Cohomology of congruence subgroups of SL(4, ℤ). II, J. Number Theory 128 (2008), 2263–2274; MR 2394820.CrossRefGoogle Scholar
Ash, A., Gunnells, P. E. and McConnell, M., Cohomology of congruence subgroups of SL4(ℤ). III, Math. Comp. 79 (2010), 1811–1831; MR 2630015.CrossRefGoogle Scholar
Ash, A., Putman, A. and Sam, S. V., Homological vanishing for the Steinberg representation, Compos. Math. 154 (2018), 1111–1130; MR 3797603.CrossRefGoogle Scholar
Ash, A. and Rudolph, L., The modular symbol and continued fractions in higher dimensions, Invent. Math. 55 (1979), 241–250; MR 553998.CrossRefGoogle Scholar
Borel, A., Stable real cohomology of arithmetic groups, Ann. Sci. Éc. Norm. Supér. (4) 7 (1974), 235–272; MR 0387496.CrossRefGoogle Scholar
Borel, A. and Serre, J.-P., Corners and arithmetic groups, Comment. Math. Helv. 48 (1973), 436–491; MR 0387495.CrossRefGoogle Scholar
Brown, K. S., Buildings (Springer, New York, 1989); MR 969123.CrossRefGoogle Scholar
Brunetti, M. and Ciampella, A., A Priddy-type Koszulness criterion for non-locally finite algebras, Colloq. Math. 109 (2007), 179–192; MR 2318516.CrossRefGoogle Scholar
Bykovskiĭ, V. A., Generating elements of the annihilating ideal for modular symbols, Funktsional. Anal. i Prilozhen. 37 (2003), 27–38; MR 2083229.CrossRefGoogle Scholar
Calegari, F., The stable homology of congruence subgroups, Geom. Topol. 19 (2015), 3149–3191; MR 3447101.CrossRefGoogle Scholar
Chardin, M. and Symonds, P., Degree bounds on homology and a conjecture of Derksen, Compos. Math. 152 (2016), 2041–2049; MR 3569999.CrossRefGoogle Scholar
Church, T. and Ellenberg, J., Homology of FI-modules, Geom. Topol. 21 (2017), 2373–2418; MR 3654111.CrossRefGoogle Scholar
Church, T., Ellenberg, J. S. and Farb, B., FI-modules and stability for representations of symmetric groups, Duke Math. J. 164 (2015), 1833–1910; MR 3357185.CrossRefGoogle Scholar
Church, T., Ellenberg, J. S., Farb, B. and Nagpal, R., FI-modules over Noetherian rings, Geom. Topol. 18 (2014), 2951–2984; MR 3285226.CrossRefGoogle Scholar
Church, T., Farb, B. and Putman, A., A stability conjecture for the unstable cohomology of SLnℤ, mapping class groups, and Aut(F n), in Algebraic topology: applications and new directions, Contemporary Mathematics, vol. 620 (American Mathematical Society, Providence, RI, 2014), 55–70; MR 3290086.Google Scholar
Church, T., Farb, B. and Putman, A., Integrality in the Steinberg module and the top-dimensional cohomology of SLn𝓞K, Amer. J. Math. 141 (2019), 1375–1419; MR 4011804.CrossRefGoogle Scholar
Charney, R., On the problem of homology stability for congruence subgroups, Comm. Algebra 12 (1984), 2081–2123; MR 747219.CrossRefGoogle Scholar
Church, T., Miller, J., Nagpal, R. and Reinhold, J., Linear and quadratic ranges in representation stability, Adv. Math. 333 (2018), 1–40.CrossRefGoogle Scholar
Church, T. and Putman, A., The codimension-one cohomology of SLnℤ, Geom. Topol. 21 (2017), 999–1032; MR 3626596.CrossRefGoogle Scholar
Djament, A., De l’homologie stable des groupes de congruence, Preprint (2015), https://hal.archives-ouvertes.fr/hal-01565891v2.Google Scholar
Dutour Sikirić, M., Elbaz-Vincent, P., Kupers, A. and Martinet, J., Voronoi complexes in higher dimensions, cohomology of $GL_{N}(Z)$for $N\geqslant 8$and the triviality of $K_{8}(Z)$, Preprint (2019), arXiv:1910.11598.Google Scholar
Dutour Sikirić, M., Gangl, H., Gunnells, P. E., Hanke, J., Schürmann, A. and Yasaki, D., On the topological computation of K 4 of the Gaussian and Eisenstein integers, J. Homotopy Relat. Struct. 14 (2019), 281–291; MR 3913976.CrossRefGoogle Scholar
Galatius, S., Kupers, A. and Randal-Williams, O., Cellular $E_{k}$-algebras, Preprint (2018),arXiv:1805.07184.Google Scholar
Gan, W. L. and Li, L., Linear stable range for homology of congruence subgroups via FI-modules, Selecta Math. (N.S.) 25 (2019), Art. 55 11; MR 3997138.CrossRefGoogle Scholar
Hausmann, J.-C., Manifolds with a given homology and fundamental group, Comment. Math. Helv. 53 (1978), 113–134; MR 483534.CrossRefGoogle Scholar
Lee, R. and Szczarba, R. H., The group K 3(Z) is cyclic of order forty-eight, Ann. of Math. (2) 104 (1976a), 31–60; MR 0442934.CrossRefGoogle Scholar
Lee, R. and Szczarba, R. H., On the homology and cohomology of congruence subgroups, Invent. Math. 33 (1976b), 15–53; MR 0422498.CrossRefGoogle Scholar
Lee, R. and Szczarba, R. H., On the torsion in K 4(Z) and K 5(Z), Duke Math. J. 45 (1978), 101–129; MR 0491893.CrossRefGoogle Scholar
Miller, J., Patzt, P. and Putman, A., On the top dimensional cohomology groups of congruence subgroups of $\text{SL}_{n}(\mathbb{Z})$, Preprint (2019), arXiv:1909.02661.Google Scholar
Miller, J., Patzt, P. and Wilson, J. C. H., Central stability for the homology of congruence subgroups and the second homology of Torelli groups, Adv. Math. 354 (2019), 106740MR 3992366.Google Scholar
Miller, J., Patzt, P., Wilson, J. C. H. and Yasaki, D., Non-integrality of some Steinberg modules, J. Topol., to appear. Preprint (2018), arXiv:1810.07683.Google Scholar
Nagpal, R., VI-modules in nondescribing characteristic, part I, Algebra Number Theory 13 (2019), 2151–2189; MR 4039499.CrossRefGoogle Scholar
Paraschivescu, A., On a generalization of the double coset formula, Duke Math. J. 89 (1997), 1–8; MR 1458968.CrossRefGoogle Scholar
Patzt, P., Central stability homology, Math. Z., to appear. Preprint (2017),arXiv:1704.04128v2.Google Scholar
Priddy, S. B., Koszul resolutions, Trans. Amer. Math. Soc. 152 (1970), 39–60; MR 0265437.CrossRefGoogle Scholar
Putman, A. and Studenmund, D., The dualizing module and top-dimensional cohomology group of $\text{GL}_{n}({\mathcal{O}})$, Preprint (2019), arXiv:1909.01217.Google Scholar
Putman, A., Stability in the homology of congruence subgroups, Invent. Math. 202 (2015), 987–1027; MR 3425385.CrossRefGoogle Scholar
Putman, A. and Sam, S. V., Representation stability and finite linear groups, Duke Math. J. 166 (2017), 2521–2598; MR 3703435.CrossRefGoogle Scholar
Quillen, D., Finite generation of the groups K i of rings of algebraic integers, in Algebraic K-theory, I: Higher K-theories (Proc. Conf., Battelle Memorial Inst., Seattle, Wash. 1972), Lecture Notes in Mathematics, vol. 341 (Springer, Berlin, 1973), 179–198; MR 0349812.Google Scholar
Sam, S. V. and Snowden, A., Stability patterns in representation theory, Forum Math. Sigma 3 (2015), e11; MR 3376738.CrossRefGoogle Scholar