Article contents
Subgraph distributions in dense random regular graphs
Published online by Cambridge University Press: 25 August 2023
Abstract
Given a connected graph 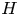 $H$ which is not a star, we show that the number of copies of
$H$ which is not a star, we show that the number of copies of 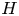 $H$ in a dense uniformly random regular graph is asymptotically Gaussian, which was not known even for
$H$ in a dense uniformly random regular graph is asymptotically Gaussian, which was not known even for 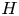 $H$ being a triangle. This addresses a question of McKay from the 2010 International Congress of Mathematicians. In fact, we prove that the behavior of the variance of the number of copies of
$H$ being a triangle. This addresses a question of McKay from the 2010 International Congress of Mathematicians. In fact, we prove that the behavior of the variance of the number of copies of 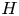 $H$ depends in a delicate manner on the occurrence and number of cycles of
$H$ depends in a delicate manner on the occurrence and number of cycles of 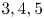 $3,4,5$ edges as well as paths of
$3,4,5$ edges as well as paths of 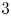 $3$ edges in
$3$ edges in 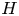 $H$. More generally, we provide control of the asymptotic distribution of certain statistics of bounded degree which are invariant under vertex permutations, including moments of the spectrum of a random regular graph. Our techniques are based on combining complex-analytic methods due to McKay and Wormald used to enumerate regular graphs with the notion of graph factors developed by Janson in the context of studying subgraph counts in
$H$. More generally, we provide control of the asymptotic distribution of certain statistics of bounded degree which are invariant under vertex permutations, including moments of the spectrum of a random regular graph. Our techniques are based on combining complex-analytic methods due to McKay and Wormald used to enumerate regular graphs with the notion of graph factors developed by Janson in the context of studying subgraph counts in 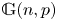 $\mathbb {G}(n,p)$.
$\mathbb {G}(n,p)$.
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- © 2023 The Author(s). The publishing rights in this article are licensed to Foundation Compositio Mathematica under an exclusive licence
Footnotes
Sah and Sawhney were supported by NSF Graduate Research Fellowship Program DGE-2141064. Sah was supported by the PD Soros Fellowship.
References
- 2
- Cited by


