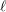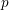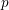Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Waldspurger, Jean-Loup
2021.
Représentations et quasi-caractères de niveau 0 ; endoscopie.
Journal de l’École polytechnique — Mathématiques,
Vol. 8,
Issue. ,
p.
193.
Lanard, Thomas
2021.
Equivalence of categories between coefficient systems and systems of idempotents.
Representation Theory of the American Mathematical Society,
Vol. 25,
Issue. 14,
p.
422.
Kurinczuk, Robert
Skodlerack, Daniel
and
Stevens, Shaun
2021.
Endo-parameters for p-adic classical groups.
Inventiones mathematicae,
Vol. 223,
Issue. 2,
p.
597.
Lanard, Thomas
2023.
Unipotent ℓ-blocks for simply connected p-adic
groups.
Algebra & Number Theory,
Vol. 17,
Issue. 9,
p.
1533.
Li, Tzu-Jan
2023.
On endomorphism algebras of Gelfand-Graev representations.
Representation Theory of the American Mathematical Society,
Vol. 27,
Issue. 5,
p.
80.