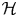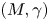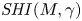1. Introduction
Let ![]() $(M,\gamma )$ be a balanced sutured manifold. Kronheimer and Mrowka conjectured [Reference Kronheimer and MrowkaKM10] that its sutured instanton homology is isomorphic to its sutured Heegaard Floer homology,
$(M,\gamma )$ be a balanced sutured manifold. Kronheimer and Mrowka conjectured [Reference Kronheimer and MrowkaKM10] that its sutured instanton homology is isomorphic to its sutured Heegaard Floer homology,
Proving this remains a major open problem. In particular, it would imply isomorphisms
 \begin{align*} I^\#(Y)&\cong \widehat{\mathit{HF}}(Y)\otimes \mathbb{C},\\ \mathit{KHI}(Y,K)&\cong \widehat{\mathit{HFK}}(Y,K)\otimes \mathbb{C}, \end{align*}
\begin{align*} I^\#(Y)&\cong \widehat{\mathit{HF}}(Y)\otimes \mathbb{C},\\ \mathit{KHI}(Y,K)&\cong \widehat{\mathit{HFK}}(Y,K)\otimes \mathbb{C}, \end{align*}
between the invariants of closed 3-manifolds and knots in the instanton and Heegaard Floer settings.
There has been a flood of recent work proving these isomorphisms for various families of closed 3-manifolds and knots; see [Reference Baldwin and SivekBS21, Reference Alfieri, Baldwin, Dai and SivekABDS22, Reference Lidman, Pinzón-Caicedo and ScadutoLPCS20, Reference Li and YeLY22, Reference Ghosh and LiGL19]. In this paper, we initiate a systematic approach to the general isomorphism (1.1). Before stating our main result, let us establish some notation.
Given a sutured Heegaard diagram
for a balanced sutured manifold ![]() $(M,\gamma )$, let
$(M,\gamma )$, let
denote the usual tori in the ![]() $k$-fold symmetric product of
$k$-fold symmetric product of ![]() $\Sigma$, and let
$\Sigma$, and let
If ![]() $\mathcal {H}$ is admissible, then
$\mathcal {H}$ is admissible, then ![]() $\mathfrak {S}(\mathcal {H})$ is the set of generators for the sutured Heegaard Floer complex
$\mathfrak {S}(\mathcal {H})$ is the set of generators for the sutured Heegaard Floer complex ![]() $\mathit {SFC}(\mathcal {H})$ as defined by Juhász in [Reference JuhászJuh06].Footnote 1 Our main theorem is the following.
$\mathit {SFC}(\mathcal {H})$ as defined by Juhász in [Reference JuhászJuh06].Footnote 1 Our main theorem is the following.
Theorem 1.1 If ![]() $\mathcal {H}$ is an admissible sutured Heegaard diagram for
$\mathcal {H}$ is an admissible sutured Heegaard diagram for ![]() $(M,\gamma )$, then
$(M,\gamma )$, then
Remark 1.2 Theorem 1.1 does not hold without the assumption that ![]() $\mathcal {H}$ is admissible; see Remark 3.6.
$\mathcal {H}$ is admissible; see Remark 3.6.
Remark 1.3 Our proof of Theorem 1.1 also works for sutured monopole homology (![]() $\mathit {SHM}$) in place of
$\mathit {SHM}$) in place of ![]() $\mathit {SHI}$. Of course, the
$\mathit {SHI}$. Of course, the ![]() $\mathit {SHM}$ version of our main result follows from the isomorphism
$\mathit {SHM}$ version of our main result follows from the isomorphism
which is a consequence of the equivalence between monopole and Heegaard Floer homology, see [Reference LekiliLek13]. Still, it may be of value to know that one can prove the inequality
without going through the proof of this equivalence.
Given a balanced sutured manifold ![]() $(M,\gamma )$, we define the simultaneous trajectory number
$(M,\gamma )$, we define the simultaneous trajectory number ![]() $\mathcal {T}(M,\gamma )$ to be the minimum of
$\mathcal {T}(M,\gamma )$ to be the minimum of ![]() $|\mathfrak {S}(\mathcal {H})|$ over all admissible sutured Heegaard diagrams
$|\mathfrak {S}(\mathcal {H})|$ over all admissible sutured Heegaard diagrams ![]() $\mathcal {H}$ for
$\mathcal {H}$ for ![]() $(M,\gamma )$. This is the generalization to balanced sutured manifolds of a notion originally defined for rational homology 3-spheres by Ozsváth and Szabó in [Reference Ozsváth and SzabóOS04a]. It admits a purely Morse-theoretic interpretation when
$(M,\gamma )$. This is the generalization to balanced sutured manifolds of a notion originally defined for rational homology 3-spheres by Ozsváth and Szabó in [Reference Ozsváth and SzabóOS04a]. It admits a purely Morse-theoretic interpretation when ![]() $H_1(M,\partial M;\mathbb {Q})=0$, and is a measure of the topological complexity of
$H_1(M,\partial M;\mathbb {Q})=0$, and is a measure of the topological complexity of ![]() $(M,\gamma )$; for example,
$(M,\gamma )$; for example, ![]() $\mathcal {T}(M,\gamma )=1$ if and only if
$\mathcal {T}(M,\gamma )=1$ if and only if ![]() $(M,\gamma )$ is a product sutured manifold.Footnote 2 Further, it is clear from the definition that
$(M,\gamma )$ is a product sutured manifold.Footnote 2 Further, it is clear from the definition that
We have the following immediate corollary of Theorem 1.1.
Corollary 1.4 If ![]() $(M,\gamma )$ is a balanced sutured manifold, then
$(M,\gamma )$ is a balanced sutured manifold, then
For the following corollaries, we recall the natural sutured manifolds associated to closed 3-manifolds and knots therein. Given a closed 3-manifold ![]() $Y$, let
$Y$, let ![]() $(Y(1),\delta )$ denote the sutured manifold obtained by removing a 3-ball from
$(Y(1),\delta )$ denote the sutured manifold obtained by removing a 3-ball from ![]() $Y$, where
$Y$, where ![]() $\delta$ is a simple closed curve on
$\delta$ is a simple closed curve on ![]() $\partial Y(1)\cong S^2$. Similarly, given a knot
$\partial Y(1)\cong S^2$. Similarly, given a knot ![]() $K\subset Y$, let
$K\subset Y$, let ![]() $(Y(K),m \cup -m)$ be the sutured manifold obtained by removing a tubular neighborhood of
$(Y(K),m \cup -m)$ be the sutured manifold obtained by removing a tubular neighborhood of ![]() $K$, where
$K$, where ![]() $m$ and
$m$ and ![]() $-m$ are oppositely oriented meridional curves on
$-m$ are oppositely oriented meridional curves on ![]() $\partial Y(K)\cong T^2$. The framed instanton and Heegaard Floer homologies of a closed 3-manifold
$\partial Y(K)\cong T^2$. The framed instanton and Heegaard Floer homologies of a closed 3-manifold ![]() $Y$ are given by
$Y$ are given by
 \begin{align*} I^\#(Y) &\cong \mathit{SHI}(Y(1),\delta), \\ \widehat{\mathit{HF}}(Y) &\cong \mathit{SFH}(Y(1),\delta). \end{align*}
\begin{align*} I^\#(Y) &\cong \mathit{SHI}(Y(1),\delta), \\ \widehat{\mathit{HF}}(Y) &\cong \mathit{SFH}(Y(1),\delta). \end{align*}
Likewise the instanton and Heegaard knot Floer homologies of a knot ![]() $K\subset Y$ are given by
$K\subset Y$ are given by
 \begin{align*} \mathit{KHI}(Y,K) &\cong \mathit{SHI}(Y(K),m\cup-m),\\ \widehat{\mathit{HFK}}(Y,K) &\cong\mathit{SFH}(Y(K),m\cup-m). \end{align*}
\begin{align*} \mathit{KHI}(Y,K) &\cong \mathit{SHI}(Y(K),m\cup-m),\\ \widehat{\mathit{HFK}}(Y,K) &\cong\mathit{SFH}(Y(K),m\cup-m). \end{align*}
Recall that the ranks of the Heegaard Floer homology and framed instanton homology of a rational homology 3-sphere ![]() $Y$ are each bounded below by
$Y$ are each bounded below by ![]() $|H_1(Y)|$. An L-space, respectively instanton L-space, is a rational homology 3-sphere which achieves these lower bounds
$|H_1(Y)|$. An L-space, respectively instanton L-space, is a rational homology 3-sphere which achieves these lower bounds
 \begin{align*} \textrm{rk}_\mathbb{Z} \widehat{\mathit{HF}}(Y) &= |H_1(Y)|, \\ \dim_\mathbb{C} I^\#(Y) &= |H_1(Y)|, \end{align*}
\begin{align*} \textrm{rk}_\mathbb{Z} \widehat{\mathit{HF}}(Y) &= |H_1(Y)|, \\ \dim_\mathbb{C} I^\#(Y) &= |H_1(Y)|, \end{align*}
respectively. A strong L-space, as defined by Levine and Lewallen in [Reference Levine and LewallenLL12], is a rational homology 3-sphere ![]() $Y$ which satisfies the stronger conditionFootnote 3
$Y$ which satisfies the stronger conditionFootnote 3
Indeed, this condition implies that ![]() $Y$ is an L-space, because
$Y$ is an L-space, because
The following is then an immediate corollary of Theorem 1.1.
Corollary 1.5 If ![]() $Y$ is a strong L-space, then it is an instanton L-space.
$Y$ is a strong L-space, then it is an instanton L-space.
More generally, we say that a sutured Heegaard diagram ![]() $\mathcal {H}$ for a sutured manifold
$\mathcal {H}$ for a sutured manifold ![]() $(M,\gamma )$ is strong if
$(M,\gamma )$ is strong if ![]() $\mathcal {H}$ is admissible and the sutured Floer complex
$\mathcal {H}$ is admissible and the sutured Floer complex ![]() $\mathit {SFC}(\mathcal {H})$ has trivial differential. We then have the following.
$\mathit {SFC}(\mathcal {H})$ has trivial differential. We then have the following.
Corollary 1.6 If ![]() $(M,\gamma )$ is a balanced sutured manifold which has a strong sutured Heegaard diagram, then
$(M,\gamma )$ is a balanced sutured manifold which has a strong sutured Heegaard diagram, then
For example, when ![]() $K$ is a
$K$ is a ![]() $(1,1)$-knot in a lens space
$(1,1)$-knot in a lens space ![]() $L(p,q)$, the sutured manifold
$L(p,q)$, the sutured manifold
has a strong Heegaard diagram. We thus reproduce the following result of Li and Ye [Reference Li and YeLY22].
Corollary 1.7 If ![]() $K\subset L(p,q)$ is a
$K\subset L(p,q)$ is a ![]() $(1,1)$-knot, then
$(1,1)$-knot, then
1.1 On the proof
Given a vertical tangle ![]() $T$ in a balanced sutured manifold
$T$ in a balanced sutured manifold ![]() $(M,\gamma )$, one forms an associated sutured manifold
$(M,\gamma )$, one forms an associated sutured manifold ![]() $(M_T,\gamma _T)$ by removing a neighborhood of
$(M_T,\gamma _T)$ by removing a neighborhood of ![]() $T$ from
$T$ from ![]() $M$, and adding meridians of the components of
$M$, and adding meridians of the components of ![]() $T$ to
$T$ to ![]() $\gamma$; see § 2 for more details. Li and Ye proved the following dimension inequality in [Reference Li and YeLY22, Proposition 3.14].
$\gamma$; see § 2 for more details. Li and Ye proved the following dimension inequality in [Reference Li and YeLY22, Proposition 3.14].
Theorem 1.8 If ![]() $T$ is a vertical tangle in
$T$ is a vertical tangle in ![]() $(M,\gamma )$ such that
$(M,\gamma )$ such that ![]() $[T_i]=0$ in
$[T_i]=0$ in ![]() $H_1(M,\partial M;\mathbb {Q})$ for each component
$H_1(M,\partial M;\mathbb {Q})$ for each component ![]() $T_i$ of
$T_i$ of ![]() $T$, then
$T$, then
To prove Theorem 1.1, we first establish the same inequality under the weaker assumption that ![]() $T$ (rather than each of its components) is rationally nullhomologous, in § 2.
$T$ (rather than each of its components) is rationally nullhomologous, in § 2.
Theorem 1.9 If ![]() $T$ is a vertical tangle in
$T$ is a vertical tangle in ![]() $(M,\gamma )$ such that
$(M,\gamma )$ such that ![]() $[T]=0$ in
$[T]=0$ in ![]() $H_1(M,\partial M;\mathbb {Q})$, then
$H_1(M,\partial M;\mathbb {Q})$, then
Next, given an admissible sutured Heegaard diagram ![]() $\mathcal {H}$ for
$\mathcal {H}$ for ![]() $(M,\gamma )$, we construct a vertical tangle
$(M,\gamma )$, we construct a vertical tangle ![]() $T\subset (M,\gamma )$ with
$T\subset (M,\gamma )$ with ![]() $[T]=0$ in
$[T]=0$ in ![]() $H_1(M,\partial M;\mathbb {Q})$, such that
$H_1(M,\partial M;\mathbb {Q})$, such that
This is the content of § 3. Theorem 1.1 then follows from Theorem 1.9.
1.2 Organization
In § 2, we prove the inequality in Theorem 1.9. We then use this in § 3 to prove our main result, Theorem 1.1. Finally, in § 4, we discuss further directions, some of which are in progress. In particular, we discuss the possibility of using the proof of Theorem 1.1 to construct a grading on ![]() $\mathit {SHI}$ by homotopy classes of 2-plane fields, and the prospects for upgrading Theorem 1.1 to a proof of the isomorphism (1.1).
$\mathit {SHI}$ by homotopy classes of 2-plane fields, and the prospects for upgrading Theorem 1.1 to a proof of the isomorphism (1.1).
2. A dimension inequality
A vertical tangle in a balanced sutured manifold ![]() $(M,\gamma )$ is a properly embedded 1-manifold
$(M,\gamma )$ is a properly embedded 1-manifold
in ![]() $M$, with boundary in
$M$, with boundary in ![]() $R(\gamma )$, whose components
$R(\gamma )$, whose components ![]() $T_i$ satisfy
$T_i$ satisfy
and are oriented from ![]() $R_+(\gamma )$ to
$R_+(\gamma )$ to ![]() $R_-(\gamma )$ (in particular,
$R_-(\gamma )$ (in particular, ![]() $T$ has no closed components). One forms an associated balanced sutured manifold
$T$ has no closed components). One forms an associated balanced sutured manifold ![]() $(M_T,\gamma _T)$ by removing tubular neighborhoods of the components
$(M_T,\gamma _T)$ by removing tubular neighborhoods of the components ![]() $T_i$, and adding positively-oriented meridians of these components to the suture
$T_i$, and adding positively-oriented meridians of these components to the suture ![]() $\gamma$, as in [Reference Li and YeLY22, § 3] and depicted in Figure 7. In this section, we prove Theorem 1.9, which states that
$\gamma$, as in [Reference Li and YeLY22, § 3] and depicted in Figure 7. In this section, we prove Theorem 1.9, which states that
when ![]() $[T]=0$ in
$[T]=0$ in ![]() $H_1(M,\partial M;\mathbb {Q})$. The rough idea is to turn
$H_1(M,\partial M;\mathbb {Q})$. The rough idea is to turn ![]() $T$ into a related tangle
$T$ into a related tangle ![]() $T'$ whose components are rationally nullhomologous, and apply Theorem 1.8.
$T'$ whose components are rationally nullhomologous, and apply Theorem 1.8.
Proof of Theorem 1.9 Let ![]() $T_1,\ldots,T_n$ be the components of
$T_1,\ldots,T_n$ be the components of ![]() $T$. For
$T$. For ![]() $i=1,\ldots,n$, let
$i=1,\ldots,n$, let
where ![]() $p_i\in R_+(\gamma )$ and
$p_i\in R_+(\gamma )$ and ![]() $q_i \in R_-(\gamma )$. We may assume that
$q_i \in R_-(\gamma )$. We may assume that ![]() $\gamma$ is connected, because we can achieve this by adding contact 1-handles to
$\gamma$ is connected, because we can achieve this by adding contact 1-handles to ![]() $(M,\gamma )$, an operation which does not change
$(M,\gamma )$, an operation which does not change ![]() $\mathit {SHI}(M,\gamma )$ (equivalently,
$\mathit {SHI}(M,\gamma )$ (equivalently, ![]() $\mathit {SHI}$ is invariant under product disk decomposition [Reference Kronheimer and MrowkaKM10, Reference Baldwin and SivekBS16]). Then we can find a sequence of pairwise disjoint arcs
$\mathit {SHI}$ is invariant under product disk decomposition [Reference Kronheimer and MrowkaKM10, Reference Baldwin and SivekBS16]). Then we can find a sequence of pairwise disjoint arcs
such that, for each ![]() $i=1,\ldots,n$, we have:
$i=1,\ldots,n$, we have:
•
 $\partial \xi _i = p_{i+1}-q_i$ (where
$\partial \xi _i = p_{i+1}-q_i$ (where  $p_{n+1}:=p_1$); and
$p_{n+1}:=p_1$); and•
 $\xi _i$ intersects
$\xi _i$ intersects  $\gamma$ in exactly one point.
$\gamma$ in exactly one point.
For every ![]() $i\in \{2,\ldots,n\}$, choose an arc
$i\in \{2,\ldots,n\}$, choose an arc ![]() $t_{i} \subset \partial M$ in a neighborhood of the unique intersection point
$t_{i} \subset \partial M$ in a neighborhood of the unique intersection point ![]() $\xi _{i-1}\cap \gamma$, as depicted in Figures 1 and 2. Push the interior of
$\xi _{i-1}\cap \gamma$, as depicted in Figures 1 and 2. Push the interior of ![]() $t_{i}$ into the interior of
$t_{i}$ into the interior of ![]() $M$ to turn this arc into a vertical tangle
$M$ to turn this arc into a vertical tangle ![]() $T_{i}'$, and let
$T_{i}'$, and let
Then
where ![]() $\mu _i'$ is a positively oriented meridian of
$\mu _i'$ is a positively oriented meridian of ![]() $T_i'$. Each component
$T_i'$. Each component ![]() $T_{i}'$ cobounds a disk in
$T_{i}'$ cobounds a disk in ![]() $M$ with the arc
$M$ with the arc ![]() $t_{i}$. These disks then restrict to properly embedded disks
$t_{i}$. These disks then restrict to properly embedded disks
with ![]() $|D_i\cap \gamma |=1$ and
$|D_i\cap \gamma |=1$ and ![]() $|D_i\cap \mu _j'|=\delta _{ij}$, so that
$|D_i\cap \mu _j'|=\delta _{ij}$, so that
Thus, each ![]() $D_i$ is a product disk.
$D_i$ is a product disk.

Figure 1. The point of view is from the interior of ![]() $M$, looking at
$M$, looking at ![]() $\partial M$.
$\partial M$.

Figure 2. The tangle ![]() $T = T_1\cup \cdots \cup T_n$ in
$T = T_1\cup \cdots \cup T_n$ in ![]() $M$ and the arcs
$M$ and the arcs ![]() $\xi _i$ and
$\xi _i$ and ![]() $t_i$ in
$t_i$ in ![]() $\partial M$, together with the suture
$\partial M$, together with the suture ![]() $\gamma$.
$\gamma$.
Next, consider the arc
Push its interior into the interior of ![]() $M_{T''}$ to form a vertical tangle
$M_{T''}$ to form a vertical tangle ![]() $T_1'$ with
$T_1'$ with ![]() $\partial T_1' = q_n-p_1,$ as in Figure 3. Let
$\partial T_1' = q_n-p_1,$ as in Figure 3. Let ![]() $T'$ be the tangle in
$T'$ be the tangle in ![]() $M$ given by
$M$ given by
We refer to a tangle ![]() $T'$ formed in this way as a mixed tangle for
$T'$ formed in this way as a mixed tangle for ![]() $T$. Note that
$T$. Note that
where ![]() $\mu _1'$ is a positively oriented meridian of
$\mu _1'$ is a positively oriented meridian of ![]() $T_1'$. Observe that the disks
$T_1'$. Observe that the disks ![]() $D_2,\ldots, D_n\subset M_{T''}$ restrict to properly embedded annuli
$D_2,\ldots, D_n\subset M_{T''}$ restrict to properly embedded annuli
because ![]() $T_1'$ intersects each disk in exactly one point, as shown in Figure 4.
$T_1'$ intersects each disk in exactly one point, as shown in Figure 4.

Figure 3. The tangle ![]() $T' = T_1' \cup \cdots \cup T_n'$ in
$T' = T_1' \cup \cdots \cup T_n'$ in ![]() $M$.
$M$.

Figure 4. The annulus ![]() $A_i$ in
$A_i$ in ![]() $M_{T'}$ near the boundaries of the tubular neighborhoods of the components
$M_{T'}$ near the boundaries of the tubular neighborhoods of the components ![]() $T_1'$ and
$T_1'$ and ![]() $T_i'$, as seen from inside
$T_i'$, as seen from inside ![]() $M_{T'}$.
$M_{T'}$.
The endpoints of the arc ![]() $\xi _n\subset \partial M_{T''}$ agree with
$\xi _n\subset \partial M_{T''}$ agree with ![]() $\partial T_1'$, and
$\partial T_1'$, and ![]() $|\xi _n\cap \gamma |=1$. We can, thus, use
$|\xi _n\cap \gamma |=1$. We can, thus, use ![]() $\xi _n$ together with
$\xi _n$ together with ![]() $\gamma$ and
$\gamma$ and ![]() $\mu _1'$ to define a sequence of sutures
$\mu _1'$ to define a sequence of sutures ![]() $\Gamma _m\subset \partial M_{T'}$ for
$\Gamma _m\subset \partial M_{T'}$ for ![]() $m\in \mathbb {N}$, as in [Reference Li and YeLY22, § 3.2], which one should regard as ‘longitudinal’ sutures for
$m\in \mathbb {N}$, as in [Reference Li and YeLY22, § 3.2], which one should regard as ‘longitudinal’ sutures for ![]() $T_1'$; see Figure 5. By the construction of
$T_1'$; see Figure 5. By the construction of ![]() $T_1'$ and the assumption that
$T_1'$ and the assumption that ![]() $T$ is rationally nullhomologous in
$T$ is rationally nullhomologous in ![]() $(M,\partial M)$, we have
$(M,\partial M)$, we have
Therefore, by [Reference Li and YeLY22, Lemmas 3.21 and 3.22], we have the following.
Lemma 2.1 There is an exact triangle

coming from the surgery exact triangle associated to surgeries on the meridian ![]() $\mu _1'$ of
$\mu _1'$ of ![]() $T_1'$. Furthermore,
$T_1'$. Furthermore, ![]() $G_m\equiv 0$ for
$G_m\equiv 0$ for ![]() $m$ sufficiently large.
$m$ sufficiently large.

Figure 5. (a) The suture ![]() $-\Gamma _{m+1}$ and the bypass arc
$-\Gamma _{m+1}$ and the bypass arc ![]() $\eta _-$ shown in bold. (b) The suture
$\eta _-$ shown in bold. (b) The suture ![]() $-\gamma _{T'}$ resulting from the bypass attachment along
$-\gamma _{T'}$ resulting from the bypass attachment along ![]() $\eta _-$, and the negatively stabilized annulus
$\eta _-$, and the negatively stabilized annulus ![]() $A_i^-\subset (-M_{T'},-\gamma _{T'})$.
$A_i^-\subset (-M_{T'},-\gamma _{T'})$.
For each ![]() $i=2,\ldots,n$ and every
$i=2,\ldots,n$ and every ![]() $m\in \mathbb {N}$, we have that
$m\in \mathbb {N}$, we have that
Let us orient each ![]() $A_i$ so that the induced orientation on
$A_i$ so that the induced orientation on ![]() $\partial A_i$ is opposite the orientation of
$\partial A_i$ is opposite the orientation of ![]() $\partial D_i$ coming from that of
$\partial D_i$ coming from that of ![]() $T_i'$, as in Figures 4 and 5. By [Reference Ghosh and LiGL19], the disks
$T_i'$, as in Figures 4 and 5. By [Reference Ghosh and LiGL19], the disks ![]() $D_2,\ldots,D_n$ induce a
$D_2,\ldots,D_n$ induce a ![]() $\mathbb {Z}^{n-1}$-grading on
$\mathbb {Z}^{n-1}$-grading on
Similarly, the annuli ![]() $A_2,\ldots,A_n$ induce a
$A_2,\ldots,A_n$ induce a ![]() $\mathbb {Z}^{n-1}$-grading on
$\mathbb {Z}^{n-1}$-grading on
for each ![]() $m\in \mathbb {N}$, and we have the following graded version of the triangle in Lemma 2.1.
$m\in \mathbb {N}$, and we have the following graded version of the triangle in Lemma 2.1.
Lemma 2.2 The exact triangle of Lemma 2.1 restricts to the exact triangle

Proof of Lemma 2.2 We prove that the map ![]() $F_{m+1}$ preserves the gradings. The arguments for the other two maps are similar.
$F_{m+1}$ preserves the gradings. The arguments for the other two maps are similar.
Let us first recall the definition of ![]() $F_{m+1}$ from [Reference Li and YeLY22, § 3]. Pick a closure
$F_{m+1}$ from [Reference Li and YeLY22, § 3]. Pick a closure
for ![]() $(-M_{T'},-\Gamma _{m+1})$ so that each annulus
$(-M_{T'},-\Gamma _{m+1})$ so that each annulus ![]() $A_i$ extends to a closed surface
$A_i$ extends to a closed surface ![]() $\bar A_i\subset Y_{m+1}$, as in [Reference LiLi21, § 3]. By the construction therein,
$\bar A_i\subset Y_{m+1}$, as in [Reference LiLi21, § 3]. By the construction therein,
for ![]() $i=2,\ldots,n$, because each component of
$i=2,\ldots,n$, because each component of ![]() $\partial A_i$ intersects
$\partial A_i$ intersects ![]() $\Gamma _{m+1}$ in two points. The sutured instanton homology of
$\Gamma _{m+1}$ in two points. The sutured instanton homology of ![]() $(-M_{T'},-\Gamma _{m+1})$ is defined as a certain direct summand
$(-M_{T'},-\Gamma _{m+1})$ is defined as a certain direct summand
of the instanton Floer homology ![]() $I_*(Y_{m+1})_{\omega _{m+1}}$ as in [Reference Kronheimer and MrowkaKM10, § 7]. The summand
$I_*(Y_{m+1})_{\omega _{m+1}}$ as in [Reference Kronheimer and MrowkaKM10, § 7]. The summand
is defined as the simultaneous (generalized) ![]() $(2i_2,\ldots,2i_n)$-eigenspace of commuting operators
$(2i_2,\ldots,2i_n)$-eigenspace of commuting operators
associated to these surfaces.
The meridian ![]() $\mu _1'$ of
$\mu _1'$ of ![]() $T_1'$ can be thought of as an embedded circle in
$T_1'$ can be thought of as an embedded circle in ![]() $Y_{m+1}$. Let
$Y_{m+1}$. Let ![]() $Y$ be the manifold obtained from
$Y$ be the manifold obtained from ![]() $Y_{m+1}$ via
$Y_{m+1}$ via ![]() $0$-surgery on
$0$-surgery on ![]() $\mu _1'$, with respect to the framing of
$\mu _1'$, with respect to the framing of ![]() $\mu _1'$ induced by
$\mu _1'$ induced by ![]() $\partial M_{T'}$. Since
$\partial M_{T'}$. Since ![]() $\mu _1'$ is disjoint from
$\mu _1'$ is disjoint from ![]() $R_{m+1}$ and the
$R_{m+1}$ and the ![]() $\bar A_i$, these surfaces survive in
$\bar A_i$, these surfaces survive in ![]() $Y$. By [Reference Baldwin and SivekBS16, § 3.3],
$Y$. By [Reference Baldwin and SivekBS16, § 3.3], ![]() $(Y,R_{m+1},\omega _{m+1})$ is a closure of
$(Y,R_{m+1},\omega _{m+1})$ is a closure of ![]() $(-M_{T''}, -\gamma _{T''})$. The map
$(-M_{T''}, -\gamma _{T''})$. The map ![]() $F_{m+1}$ is then induced by the cobordism given by the trace of
$F_{m+1}$ is then induced by the cobordism given by the trace of ![]() $0$-surgery on
$0$-surgery on ![]() $\mu _1'$. Since
$\mu _1'$. Since ![]() $\bar A_i\subset Y_{m+1}$ is homologous to
$\bar A_i\subset Y_{m+1}$ is homologous to ![]() $\bar A_i\subset Y$ in this cobordism,
$\bar A_i\subset Y$ in this cobordism, ![]() $F_{m+1}$ respects the eigenspaces of
$F_{m+1}$ respects the eigenspaces of ![]() $\mu (\bar A_i)$. Thus,
$\mu (\bar A_i)$. Thus, ![]() $F_{m+1}$ maps
$F_{m+1}$ maps
into
Now, the ![]() $0$-surgery on
$0$-surgery on ![]() $\mu _1'$ makes each
$\mu _1'$ makes each ![]() $\bar A_i$ compressible in
$\bar A_i$ compressible in ![]() $Y$; in particular, each
$Y$; in particular, each ![]() $\bar A_i\subset Y$ is homologous to the disjoint union of two tori
$\bar A_i\subset Y$ is homologous to the disjoint union of two tori
One of these tori, say ![]() $T_i^1$, is the extension
$T_i^1$, is the extension ![]() $\bar D_i\subset Y$ of
$\bar D_i\subset Y$ of ![]() $D_i\subset -M_{T''}$ that is used to define the grading on
$D_i\subset -M_{T''}$ that is used to define the grading on ![]() $\mathit {SHI}(-M_{T''},-\gamma _{T''})$ associated to
$\mathit {SHI}(-M_{T''},-\gamma _{T''})$ associated to ![]() $D_i$. Since
$D_i$. Since
in ![]() $H_2(Y)$, the
$H_2(Y)$, the ![]() $k$-eigenspace of
$k$-eigenspace of ![]() $\mu (\bar A_i)$ agrees with the
$\mu (\bar A_i)$ agrees with the ![]() $k$-eigenspace of
$k$-eigenspace of ![]() $\mu (\bar D_i)$ for every
$\mu (\bar D_i)$ for every ![]() $k$, by [Reference Baldwin and SivekBS22, Corollary 2.9]. Thus, we have that
$k$, by [Reference Baldwin and SivekBS22, Corollary 2.9]. Thus, we have that
Putting these arguments together, we see that ![]() $F_{m+1}$ preserves the
$F_{m+1}$ preserves the ![]() $\mathbb {Z}^{n-1}$-gradings as claimed in the lemma.
$\mathbb {Z}^{n-1}$-gradings as claimed in the lemma.
Note that decomposing ![]() $(-M_{T''},-\gamma _{T''})$ along
$(-M_{T''},-\gamma _{T''})$ along ![]() $D_2\cup \cdots \cup D_n$ yields
$D_2\cup \cdots \cup D_n$ yields ![]() $(-M,-\gamma )$. By [Reference LiLi21, Lemma 4.2], we therefore have
$(-M,-\gamma )$. By [Reference LiLi21, Lemma 4.2], we therefore have
Hence, for ![]() $m$ sufficiently large, Lemmas 2.1 and 2.2 imply that
$m$ sufficiently large, Lemmas 2.1 and 2.2 imply that
since ![]() $G_m\equiv 0$.
$G_m\equiv 0$.
Next, we consider attaching a bypass to ![]() $(-M_{T'},-\Gamma _{m+1})$ along the arc
$(-M_{T'},-\Gamma _{m+1})$ along the arc ![]() $\eta _-$ in Figure 5. By [Reference Baldwin and SivekBS22, § 4], this attachment gives rise to a bypass exact triangle. As discussed in [Reference Li and YeLY22, § 3], the other two sutures involved in the triangle are
$\eta _-$ in Figure 5. By [Reference Baldwin and SivekBS22, § 4], this attachment gives rise to a bypass exact triangle. As discussed in [Reference Li and YeLY22, § 3], the other two sutures involved in the triangle are ![]() $-\Gamma _m$ and
$-\Gamma _m$ and ![]() $-\gamma _{T'}$. It is straightforward to check that the bypass attachment along
$-\gamma _{T'}$. It is straightforward to check that the bypass attachment along ![]() $\eta _-$ creates a negative stabilization
$\eta _-$ creates a negative stabilization
of ![]() $A_i$, for each
$A_i$, for each ![]() $i=2,\ldots,n$, in the sense of [Reference LiLi21, Definition 3.1]. Hence, as in the proof of [Reference LiLi21, Proposition 5.5], we have the following graded version of the bypass exact triangle of [Reference Baldwin and SivekBS22, Theorem 1.20]:
$i=2,\ldots,n$, in the sense of [Reference LiLi21, Definition 3.1]. Hence, as in the proof of [Reference LiLi21, Proposition 5.5], we have the following graded version of the bypass exact triangle of [Reference Baldwin and SivekBS22, Theorem 1.20]:

which implies that
 \begin{align} &\dim_\mathbb{C}\mathit{SHI}(-M_{T'},-\gamma_{T'},(A_2^-,\ldots,A_n^-), (0,\ldots,0))\nonumber\\ &\quad \geq\dim_\mathbb{C}\mathit{SHI}(-M_{T'},-\Gamma_{m+1},(A_2,\ldots,A_n), (0,\ldots,0))\nonumber\\ &\qquad -\dim_\mathbb{C}\mathit{SHI}(-M_{T'},-\Gamma_{m},(A_2,\ldots,A_n), (0,\ldots,0)). \end{align}
\begin{align} &\dim_\mathbb{C}\mathit{SHI}(-M_{T'},-\gamma_{T'},(A_2^-,\ldots,A_n^-), (0,\ldots,0))\nonumber\\ &\quad \geq\dim_\mathbb{C}\mathit{SHI}(-M_{T'},-\Gamma_{m+1},(A_2,\ldots,A_n), (0,\ldots,0))\nonumber\\ &\qquad -\dim_\mathbb{C}\mathit{SHI}(-M_{T'},-\Gamma_{m},(A_2,\ldots,A_n), (0,\ldots,0)). \end{align}From the grading shifting property [Reference LiLi21, Theorem 1.12] and [Reference WangWan20, Proposition 4.1], we have
 \begin{align} &\mathit{SHI}(-M_{T'},-\gamma_{T'},(A_2^-,\ldots,A_n^-), (0,\ldots,0)) \nonumber\\ &\quad = \mathit{SHI}(-M_{T'},-\gamma_{T'},(A_2^+,\ldots,A_n^+), (-1,\ldots,-1)), \end{align}
\begin{align} &\mathit{SHI}(-M_{T'},-\gamma_{T'},(A_2^-,\ldots,A_n^-), (0,\ldots,0)) \nonumber\\ &\quad = \mathit{SHI}(-M_{T'},-\gamma_{T'},(A_2^+,\ldots,A_n^+), (-1,\ldots,-1)), \end{align}
where ![]() $A_i^+$ is a positive stabilization of
$A_i^+$ is a positive stabilization of ![]() $A_i$. Moreover, from the construction of the gradings and stabilizations in [Reference LiLi21, § 3], we have
$A_i$. Moreover, from the construction of the gradings and stabilizations in [Reference LiLi21, § 3], we have
 \begin{align} &\mathit{SHI}(-M_{T'},-\gamma_{T'},(A_2^+,\ldots,A_n^+), (-1,\ldots,-1)) \nonumber\\ &\quad = \mathit{SHI}(-M_{T'},-\gamma_{T'},(-(A_2^+),\ldots,-(A_n^+)), (1,\ldots,1))\nonumber\\ &\quad =\mathit{SHI}(-M_{T'},-\gamma_{T'},((-A_2)^-,\ldots,(-A_n)^-), (1,\ldots,1)). \end{align}
\begin{align} &\mathit{SHI}(-M_{T'},-\gamma_{T'},(A_2^+,\ldots,A_n^+), (-1,\ldots,-1)) \nonumber\\ &\quad = \mathit{SHI}(-M_{T'},-\gamma_{T'},(-(A_2^+),\ldots,-(A_n^+)), (1,\ldots,1))\nonumber\\ &\quad =\mathit{SHI}(-M_{T'},-\gamma_{T'},((-A_2)^-,\ldots,(-A_n)^-), (1,\ldots,1)). \end{align}
By [Reference LiLi21, Lemma 4.2], this last group is isomorphic to the sutured instanton homology of the manifold obtained from ![]() $(-M_{T'},-\gamma _{T'})$ by decomposing along
$(-M_{T'},-\gamma _{T'})$ by decomposing along ![]() $(-A_2)^-\cup \cdots \cup (-A_n)^-$. By [Reference LiLi21, Lemma 3.2], this is the same as the manifold obtained by decomposing along
$(-A_2)^-\cup \cdots \cup (-A_n)^-$. By [Reference LiLi21, Lemma 3.2], this is the same as the manifold obtained by decomposing along ![]() $-A_2\cup \cdots \cup -A_n$, which is, after reversing orientation, the manifold obtained from
$-A_2\cup \cdots \cup -A_n$, which is, after reversing orientation, the manifold obtained from ![]() $(M_{T'},\gamma _{T'})$ by decomposing along
$(M_{T'},\gamma _{T'})$ by decomposing along ![]() $A_2\cup \cdots \cup A_n$. It is straightforward to check that the latter manifold is simply
$A_2\cup \cdots \cup A_n$. It is straightforward to check that the latter manifold is simply ![]() $(M_T,\gamma _T)$, as indicated in Figure 6 in the case
$(M_T,\gamma _T)$, as indicated in Figure 6 in the case ![]() $n=2$. Thus,
$n=2$. Thus,

Figure 6. The result of decomposing ![]() $(M_{T'},\gamma _{T'})$ along
$(M_{T'},\gamma _{T'})$ along ![]() $A_2\cup \cdots \cup A_n$ is simply
$A_2\cup \cdots \cup A_n$ is simply ![]() $(M_T,\gamma _T)$. This is illustrated above in the case
$(M_T,\gamma _T)$. This is illustrated above in the case ![]() $n=2$.
$n=2$.
Finally, combining (2.1)–(2.5), we have that
 \begin{align*} \dim_\mathbb{C}\mathit{SHI}(-M_T,-\gamma_T)&=\dim_\mathbb{C}\mathit{SHI}(-M_{T'},-\gamma_{T'},((-A_2)^-,\ldots,(-A_n)^-), (1,\ldots,1))\\ &=\dim_\mathbb{C}\mathit{SHI}(-M_{T'},-\gamma_{T'},(A_2^-,\ldots,A_n^-), (0,\ldots,0)) \\ &\geq\dim_\mathbb{C}\mathit{SHI}(-M_{T'},-\Gamma_{m+1},(A_2,\ldots,A_n), (0,\ldots,0))\\ &\quad-\dim_\mathbb{C}\mathit{SHI}(-M_{T'},-\Gamma_{m},(A_2,\ldots,A_n), (0,\ldots,0))\\ &=\dim_\mathbb{C}\mathit{SHI}(-M,-\gamma). \end{align*}
\begin{align*} \dim_\mathbb{C}\mathit{SHI}(-M_T,-\gamma_T)&=\dim_\mathbb{C}\mathit{SHI}(-M_{T'},-\gamma_{T'},((-A_2)^-,\ldots,(-A_n)^-), (1,\ldots,1))\\ &=\dim_\mathbb{C}\mathit{SHI}(-M_{T'},-\gamma_{T'},(A_2^-,\ldots,A_n^-), (0,\ldots,0)) \\ &\geq\dim_\mathbb{C}\mathit{SHI}(-M_{T'},-\Gamma_{m+1},(A_2,\ldots,A_n), (0,\ldots,0))\\ &\quad-\dim_\mathbb{C}\mathit{SHI}(-M_{T'},-\Gamma_{m},(A_2,\ldots,A_n), (0,\ldots,0))\\ &=\dim_\mathbb{C}\mathit{SHI}(-M,-\gamma). \end{align*}
Given the symmetry of ![]() $\mathit {SHI}$ under orientation reversal, this proves Theorem 1.9.
$\mathit {SHI}$ under orientation reversal, this proves Theorem 1.9.
3. Proof of Theorem 1.1
3.1 Full tangles
Let ![]() $(M,\gamma )$ be a balanced sutured manifold. Let
$(M,\gamma )$ be a balanced sutured manifold. Let
be any (not necessarily admissible) sutured Heegaard diagram for ![]() $(M,\gamma )$. This means that
$(M,\gamma )$. This means that ![]() $M$ is obtained from
$M$ is obtained from ![]() $\Sigma \times [-1,1]$ by attaching 3-dimensional 2-handles
$\Sigma \times [-1,1]$ by attaching 3-dimensional 2-handles
 \begin{align*} \mathbb{D}_{\alpha_i} &=D_{\alpha_i}^2\times I,\\ \mathbb{D}_{\beta_i} &=D_{\beta_i}^2\times I, \end{align*}
\begin{align*} \mathbb{D}_{\alpha_i} &=D_{\alpha_i}^2\times I,\\ \mathbb{D}_{\beta_i} &=D_{\beta_i}^2\times I, \end{align*}
along ![]() $A_i\times \{-1\}$ and
$A_i\times \{-1\}$ and ![]() $B_i\times \{+1\}$, where
$B_i\times \{+1\}$, where ![]() $A_i$ and
$A_i$ and ![]() $B_i$ are annular neighborhoods of
$B_i$ are annular neighborhoods of ![]() $\alpha _i$ and
$\alpha _i$ and ![]() $\beta _i$, respectively, for
$\beta _i$, respectively, for ![]() $i=1,\ldots,k$. The suture
$i=1,\ldots,k$. The suture ![]() $\gamma$ is given by
$\gamma$ is given by
We next define a special class of vertical tangles in ![]() $(M,\gamma )$ associated to
$(M,\gamma )$ associated to ![]() $\mathcal {H}$.
$\mathcal {H}$.
Let ![]() $R_1,\ldots,R_n$ be the regions of
$R_1,\ldots,R_n$ be the regions of ![]() $\Sigma$–
$\Sigma$–![]() $\alpha$–
$\alpha$–![]() $\beta$ disjoint from
$\beta$ disjoint from ![]() $\partial \Sigma$. For each
$\partial \Sigma$. For each ![]() $i=1,\ldots,n$, let
$i=1,\ldots,n$, let ![]() $p_{i1},\ldots,p_{ia_i}$ be
$p_{i1},\ldots,p_{ia_i}$ be ![]() $a_i$ distinct points in
$a_i$ distinct points in ![]() $R_i$, for some integer
$R_i$, for some integer ![]() $a_i\geq 1$. Let
$a_i\geq 1$. Let
and let
 \[ T = \bigcup_{i=1}^n \bigcup_{j=1}^{a_i} T_{ij}. \]
\[ T = \bigcup_{i=1}^n \bigcup_{j=1}^{a_i} T_{ij}. \]
Then ![]() $T$ is a vertical tangle in
$T$ is a vertical tangle in ![]() $(M,\gamma )$, oriented from
$(M,\gamma )$, oriented from ![]() $R_+(\gamma )$ to
$R_+(\gamma )$ to ![]() $R_-(\gamma )$. Let
$R_-(\gamma )$. Let ![]() $D_{ij}^2$ be a tubular neighborhood of the point
$D_{ij}^2$ be a tubular neighborhood of the point ![]() $p_{ij}\in R_i$, let
$p_{ij}\in R_i$, let
be a tubular neighborhood of the component ![]() $T_{ij}$ in
$T_{ij}$ in ![]() $M$, and let
$M$, and let
be a positively oriented meridian of this component; see Figure 7. Let ![]() $(M_T, \gamma _T)$ be the balanced sutured manifold obtained from
$(M_T, \gamma _T)$ be the balanced sutured manifold obtained from ![]() $M$ by removing these tubular neighborhoods,
$M$ by removing these tubular neighborhoods,
 \[ M_T = M-\bigcup_{i=1}^n\bigcup_{j=1}^{a_i}N_{ij}, \]
\[ M_T = M-\bigcup_{i=1}^n\bigcup_{j=1}^{a_i}N_{ij}, \]
where ![]() $\gamma _T$ is the union of
$\gamma _T$ is the union of ![]() $\gamma$ with meridians of the
$\gamma$ with meridians of the ![]() $T_{ij}$,
$T_{ij}$,
 \[ \gamma_T = \gamma\cup \bigcup_{i=1}^n\bigcup_{j=1}^{a_i}\gamma_{ij}, \]
\[ \gamma_T = \gamma\cup \bigcup_{i=1}^n\bigcup_{j=1}^{a_i}\gamma_{ij}, \]
as in § 2. We refer to any tangle obtained in this way as a full tangle for ![]() $\mathcal {H}$.
$\mathcal {H}$.

Figure 7. (a) The component ![]() $T_{ij}=p_{ij}\times [-1,1]\subset M$. (b) The complement of
$T_{ij}=p_{ij}\times [-1,1]\subset M$. (b) The complement of ![]() $N_{ij}$ with the meridian
$N_{ij}$ with the meridian ![]() $\gamma _{ij}$.
$\gamma _{ij}$.
The main result of this section is the following.
Proposition 3.1 If ![]() $T$ is a full tangle for
$T$ is a full tangle for ![]() $\mathcal {H}$, then
$\mathcal {H}$, then ![]() $\dim _\mathbb {C}\mathit {SHI}(M_T,\gamma _T) = |\mathfrak {S}(\mathcal {H})|.$
$\dim _\mathbb {C}\mathit {SHI}(M_T,\gamma _T) = |\mathfrak {S}(\mathcal {H})|.$
Remark 3.2 The analogue of this proposition for ![]() $\mathit {SFH}$ is immediate. One forms a sutured Heegaard diagram
$\mathit {SFH}$ is immediate. One forms a sutured Heegaard diagram ![]() $\mathcal {H}_T$ for
$\mathcal {H}_T$ for ![]() $(M_T,\gamma _T)$ from
$(M_T,\gamma _T)$ from ![]() $\mathcal {H}$ by removing neighborhoods of the
$\mathcal {H}$ by removing neighborhoods of the ![]() $p_{ij}\in \Sigma$. Since there is at least one such point in every region of
$p_{ij}\in \Sigma$. Since there is at least one such point in every region of ![]() $\Sigma$–
$\Sigma$–![]() $\alpha$–
$\alpha$–![]() $\beta$ not intersecting
$\beta$ not intersecting ![]() $\partial \Sigma$, this ensures that
$\partial \Sigma$, this ensures that ![]() $\mathcal {H}_T$ is admissible and that the differential on
$\mathcal {H}_T$ is admissible and that the differential on ![]() $\mathit {SFC}(\mathcal {H}_T)$ is zero, so that
$\mathit {SFC}(\mathcal {H}_T)$ is zero, so that
This was the inspiration for our result above.
We need the following for the proof of Proposition 3.1; see [Reference Ghosh and LiGL19, Corollary 4.3].
Proposition 3.3 Suppose ![]() $(M,\gamma )$ is an irreducible balanced sutured manifold and
$(M,\gamma )$ is an irreducible balanced sutured manifold and ![]() $D\subset M$ is a properly embedded disk which intersects
$D\subset M$ is a properly embedded disk which intersects ![]() $\gamma$ in four points. Then
$\gamma$ in four points. Then
where ![]() $(M',\gamma ')$ and
$(M',\gamma ')$ and ![]() $(M'',\gamma '')$ are the decompositions of
$(M'',\gamma '')$ are the decompositions of ![]() $(M,\gamma )$ along
$(M,\gamma )$ along ![]() $D$ and
$D$ and ![]() $-D$, respectively.
$-D$, respectively.
Before proving this proposition, we record the following lemma. This lemma is well-known (Kronheimer and Mrowka prove the much harder converse in [Reference Kronheimer and MrowkaKM10, Theorem 7.12]), but since we could not find a concrete reference in the literature we provide a short proof here.
Lemma 3.4 Suppose ![]() $(M,\gamma )$ is an irreducible balanced sutured manifold. If
$(M,\gamma )$ is an irreducible balanced sutured manifold. If ![]() $(M,\gamma )$ is not taut, then
$(M,\gamma )$ is not taut, then ![]() $\mathit {SHI}(M,\gamma )= 0$.
$\mathit {SHI}(M,\gamma )= 0$.
Proof. As mentioned in the proof of Lemma 2.2, ![]() $\mathit {SHI}(M,\gamma )$ is defined in [Reference Kronheimer and MrowkaKM10, § 7] in terms of a closure
$\mathit {SHI}(M,\gamma )$ is defined in [Reference Kronheimer and MrowkaKM10, § 7] in terms of a closure ![]() $(Y,R,\omega )$ of
$(Y,R,\omega )$ of ![]() $(M,\gamma )$, where
$(M,\gamma )$, where ![]() $Y$ is a closed oriented
$Y$ is a closed oriented ![]() $3$-manifold,
$3$-manifold, ![]() $R\subset Y$ is a connected closed oriented surface which we can take to have genus
$R\subset Y$ is a connected closed oriented surface which we can take to have genus ![]() $g(R)>1$, and
$g(R)>1$, and ![]() $\omega \subset Y$ is a simple closed curve with
$\omega \subset Y$ is a simple closed curve with ![]() $|\omega \cap R|=1$. Specifically,
$|\omega \cap R|=1$. Specifically, ![]() $\mathit {SHI}(M,\gamma )$ is the generalized
$\mathit {SHI}(M,\gamma )$ is the generalized ![]() $(2g(R){-}2)$-eigenspace of the operator
$(2g(R){-}2)$-eigenspace of the operator ![]() $\mu (R)$ on
$\mu (R)$ on ![]() $I_*(Y)_\omega$.
$I_*(Y)_\omega$.
Now suppose that ![]() $(M,\gamma )$ is irreducible but not taut. Then, by the definition of tautness (e.g. [Reference JuhászJuh06, Definition 9.18]), either one of
$(M,\gamma )$ is irreducible but not taut. Then, by the definition of tautness (e.g. [Reference JuhászJuh06, Definition 9.18]), either one of ![]() $R_{\pm }(\gamma )$ is compressible or
$R_{\pm }(\gamma )$ is compressible or ![]() $R_{\pm }(\gamma )$ do not minimize the Thurston-norm in their homology classes. In either case, there exists a surface
$R_{\pm }(\gamma )$ do not minimize the Thurston-norm in their homology classes. In either case, there exists a surface ![]() $R'\subset Y$ such that
$R'\subset Y$ such that ![]() $[R']=[R]\in H_2(Y)$ but
$[R']=[R]\in H_2(Y)$ but ![]() $1\leq g(R')< g(R)$. This implies that
$1\leq g(R')< g(R)$. This implies that ![]() $\mathit {SHI}(M,\gamma )=0$ by [Reference Kronheimer and MrowkaKM10, Proposition 7.5].
$\mathit {SHI}(M,\gamma )=0$ by [Reference Kronheimer and MrowkaKM10, Proposition 7.5].
Proof of Proposition 3.3 Ghosh and Li prove this in [Reference Ghosh and LiGL19, Corollary 4.3] under the additional assumption that ![]() $(M,\gamma )$ is taut and at least one of
$(M,\gamma )$ is taut and at least one of ![]() $(M',\gamma ')$ and
$(M',\gamma ')$ and ![]() $(M'',\gamma '')$ is taut. We show that this additional assumption is unnecessary, by showing that the proposition still holds when the assumption is not true.
$(M'',\gamma '')$ is taut. We show that this additional assumption is unnecessary, by showing that the proposition still holds when the assumption is not true.
First, suppose ![]() $(M,\gamma )$ is not taut. Then neither
$(M,\gamma )$ is not taut. Then neither ![]() $(M',\gamma ')$ nor
$(M',\gamma ')$ nor ![]() $(M'',\gamma '')$ is taut, by [Reference GabaiGab87, Lemma 0.4]. Note that the irreducibility of
$(M'',\gamma '')$ is taut, by [Reference GabaiGab87, Lemma 0.4]. Note that the irreducibility of ![]() $M$ implies the irreducibility of any manifold obtained by cutting
$M$ implies the irreducibility of any manifold obtained by cutting ![]() $M$ open along a properly embedded disk; in particular,
$M$ open along a properly embedded disk; in particular, ![]() $M'$ and
$M'$ and ![]() $M''$ are irreducible. Therefore,
$M''$ are irreducible. Therefore,
by Lemma 3.4, and the proposition holds.
Next, suppose neither ![]() $(M',\gamma ')$ nor
$(M',\gamma ')$ nor ![]() $(M'',\gamma '')$ is taut. Consider the bypass exact triangle of [Reference Baldwin and SivekBS22]:
$(M'',\gamma '')$ is taut. Consider the bypass exact triangle of [Reference Baldwin and SivekBS22]:

determined by an initial bypass attachment to ![]() $(M,\gamma )$ along an arc in
$(M,\gamma )$ along an arc in ![]() $\partial D$ as shown in Figure 8. The other manifolds
$\partial D$ as shown in Figure 8. The other manifolds ![]() $(M,\gamma '_1)$ and
$(M,\gamma '_1)$ and ![]() $(M,\gamma ''_1)$ in the triangle product disk decompose (along a copy of
$(M,\gamma ''_1)$ in the triangle product disk decompose (along a copy of ![]() $D$ which intersects the new sutures in two points) to
$D$ which intersects the new sutures in two points) to ![]() $(M',\gamma ')$ and
$(M',\gamma ')$ and ![]() $(M'',\gamma '')$, respectively. Since
$(M'',\gamma '')$, respectively. Since ![]() $\mathit {SHI}$ is invariant under product disk decomposition, we therefore have
$\mathit {SHI}$ is invariant under product disk decomposition, we therefore have
by Lemma 3.4. It then follows from the bypass triangle, and the symmetry of ![]() $\mathit {SHI}$ under orientation reversal, that
$\mathit {SHI}$ under orientation reversal, that ![]() $\mathit {SHI}(M,\gamma )=0$ as well, so the proposition holds.
$\mathit {SHI}(M,\gamma )=0$ as well, so the proposition holds.
Proof of Proposition 3.1 Recall that ![]() $D_{ij}^2$ denotes a tubular neighborhood of
$D_{ij}^2$ denotes a tubular neighborhood of ![]() $p_{ij}\in R_i$. There exists a (possibly empty) set of disjoint, properly embedded arcs
$p_{ij}\in R_i$. There exists a (possibly empty) set of disjoint, properly embedded arcs
 \begin{align*} d_1,\ldots,d_m\subset \Sigma-\bigcup_{i=1}^{n}\bigcup_{j=1}^{a_i} D_{ij} \end{align*}
\begin{align*} d_1,\ldots,d_m\subset \Sigma-\bigcup_{i=1}^{n}\bigcup_{j=1}^{a_i} D_{ij} \end{align*}
which satisfy the following three conditions:
(1) for every
 $e=1,\ldots,m$, the arc
$e=1,\ldots,m$, the arc  $d_e$ is contained in some region of
$d_e$ is contained in some region of  $\Sigma$–
$\Sigma$– $\alpha$–
$\alpha$– $\beta$;
$\beta$;(2) for every
 $e$, either both endpoints of
$e$, either both endpoints of  $d_e$ are on
$d_e$ are on  $\partial \Sigma$, or each is on some
$\partial \Sigma$, or each is on some  $\partial D_{ij}^2$; and
$\partial D_{ij}^2$; and(3)
 $\Sigma -\bigcup _{i=1}^{n}\bigcup _{j=1}^{a_i} D_{ij} - d_1-\ldots - d_m$ deformation retracts onto
$\Sigma -\bigcup _{i=1}^{n}\bigcup _{j=1}^{a_i} D_{ij} - d_1-\ldots - d_m$ deformation retracts onto  $\alpha \cup \beta$.
$\alpha \cup \beta$.
Now consider the disk
 \[ \delta_e = d_e\times[-1,1]\subset \biggl(\Sigma-\bigcup_{i=1}^{n}\bigcup_{j=1}^{a_i} D_{ij} \biggr)\times [-1,1] \subset \partial M_T, \]
\[ \delta_e = d_e\times[-1,1]\subset \biggl(\Sigma-\bigcup_{i=1}^{n}\bigcup_{j=1}^{a_i} D_{ij} \biggr)\times [-1,1] \subset \partial M_T, \]
for ![]() $e=1,\ldots,m$. The boundary of each
$e=1,\ldots,m$. The boundary of each ![]() $\delta _e$ intersects
$\delta _e$ intersects ![]() $\gamma _T$ in two points; hence,
$\gamma _T$ in two points; hence, ![]() $\delta _e$ is a product disk. Since
$\delta _e$ is a product disk. Since ![]() $\mathit {SHI}$ is invariant under product disk decomposition, let
$\mathit {SHI}$ is invariant under product disk decomposition, let ![]() $(M_T,\gamma _T)$ henceforth refer to the balanced sutured manifold obtained after decomposing along
$(M_T,\gamma _T)$ henceforth refer to the balanced sutured manifold obtained after decomposing along ![]() $\delta _1,\ldots,\delta _m$.
$\delta _1,\ldots,\delta _m$.

Figure 8. (a) A neighborhood of the disk ![]() $D\subset M$ whose boundary intersects the suture
$D\subset M$ whose boundary intersects the suture ![]() $\gamma$ in four points. (b–d) The arc of attachment for the initial bypass in the triangle.
$\gamma$ in four points. (b–d) The arc of attachment for the initial bypass in the triangle.
Then ![]() $M_T$ admits the following description. Let
$M_T$ admits the following description. Let ![]() $q_1,\ldots,q_t$ denote the intersection points between the
$q_1,\ldots,q_t$ denote the intersection points between the ![]() $\alpha$ and
$\alpha$ and ![]() $\beta$ curves. If
$\beta$ curves. If ![]() $q_\ell$ is an intersection point between
$q_\ell$ is an intersection point between ![]() $\alpha _i$ and
$\alpha _i$ and ![]() $\beta _j$, let
$\beta _j$, let ![]() $r_\ell \subset \Sigma$ denote the rectangular component of
$r_\ell \subset \Sigma$ denote the rectangular component of ![]() $A_i\cap B_j$ which contains
$A_i\cap B_j$ which contains ![]() $q_\ell$. Then
$q_\ell$. Then ![]() $M_T$ is the given by the union
$M_T$ is the given by the union
of the usual 2-handles with the tubes
as shown in Figure 9. Let ![]() $c_\ell$ denote the union of the four corners of the rectangle
$c_\ell$ denote the union of the four corners of the rectangle ![]() $r_\ell$. Then the suture
$r_\ell$. Then the suture ![]() $\gamma _T$ is given by
$\gamma _T$ is given by
 \[ \gamma_T = \bigcup_{i=1}^k (\partial D_{\alpha_i}^2 \times \partial I)\cup \bigcup_{i=1}^k (\partial D_{\beta_i}^2 \times \partial I) \cup \bigcup_{\ell=1}^t (c_\ell \times[-1,1]) - \bigcup_{\ell=1}^t (\partial r_\ell\times\{-1,1\}) \]
\[ \gamma_T = \bigcup_{i=1}^k (\partial D_{\alpha_i}^2 \times \partial I)\cup \bigcup_{i=1}^k (\partial D_{\beta_i}^2 \times \partial I) \cup \bigcup_{\ell=1}^t (c_\ell \times[-1,1]) - \bigcup_{\ell=1}^t (\partial r_\ell\times\{-1,1\}) \]
as shown and oriented in the figure near a tube ![]() $\tau _\ell$. Let
$\tau _\ell$. Let
denote the meridional disk of ![]() $\tau _\ell$, oriented as in Figure 9, for
$\tau _\ell$, oriented as in Figure 9, for ![]() $\ell =1,\ldots,t$. Note that the boundary of each
$\ell =1,\ldots,t$. Note that the boundary of each ![]() $m_\ell$ intersects the suture
$m_\ell$ intersects the suture ![]() $\gamma _T$ in four points.
$\gamma _T$ in four points.

Figure 9. (a) An intersection point ![]() $q_\ell \in \alpha _i\cap \beta _j$. The rectangular component
$q_\ell \in \alpha _i\cap \beta _j$. The rectangular component ![]() $r_\ell$ of
$r_\ell$ of ![]() $A_i\cap B_j$ containing
$A_i\cap B_j$ containing ![]() $q_\ell$ is shown in darker gray. (b) The 2-handles
$q_\ell$ is shown in darker gray. (b) The 2-handles ![]() $\mathbb {D}_{\alpha _i}$ and
$\mathbb {D}_{\alpha _i}$ and ![]() $\mathbb {D}_{\beta _j}$ glued together by the tube
$\mathbb {D}_{\beta _j}$ glued together by the tube ![]() $\tau _\ell$. The meridional disk
$\tau _\ell$. The meridional disk ![]() $m_\ell$ is shown in gray; it intersects the suture
$m_\ell$ is shown in gray; it intersects the suture ![]() $\gamma _T$ in four points, and its oriented normal points upwards. (c) The result of decomposing along
$\gamma _T$ in four points, and its oriented normal points upwards. (c) The result of decomposing along ![]() $-m_\ell$. (d) The result of decomposing along
$-m_\ell$. (d) The result of decomposing along ![]() $m_\ell$.
$m_\ell$.
Note that ![]() $M_T$ is a handlebody and therefore irreducible. We may thus apply Proposition 3.3 to it, as well as to the manifolds obtained by decomposing
$M_T$ is a handlebody and therefore irreducible. We may thus apply Proposition 3.3 to it, as well as to the manifolds obtained by decomposing ![]() $M_T$ along any collection of the meridional disks
$M_T$ along any collection of the meridional disks ![]() $m_\ell$, as these manifolds are simply disjoint unions of handlebodies and, hence, also irreducible. For each
$m_\ell$, as these manifolds are simply disjoint unions of handlebodies and, hence, also irreducible. For each ![]() $t$-tuple of signs
$t$-tuple of signs
let ![]() $(M_T^I,\gamma _T^I)$ be the sutured manifold obtained by decomposing
$(M_T^I,\gamma _T^I)$ be the sutured manifold obtained by decomposing ![]() $(M_T,\gamma _T)$ along the disks
$(M_T,\gamma _T)$ along the disks
Then
by Proposition 3.3. Each ![]() $(M_T^I,\gamma _T^I)$ is simply a union of 3-balls
$(M_T^I,\gamma _T^I)$ is simply a union of 3-balls
which means that ![]() $\mathit {SHI}(M_T^I,\gamma _T^I)$ is either
$\mathit {SHI}(M_T^I,\gamma _T^I)$ is either ![]() $\mathbb {C}$ or trivial, according as whether
$\mathbb {C}$ or trivial, according as whether ![]() $\gamma _T^I$ has exactly one component on the boundary of each of these 3-balls or not. We claim that the nonzero summands
$\gamma _T^I$ has exactly one component on the boundary of each of these 3-balls or not. We claim that the nonzero summands ![]() $\mathit {SHI}(M_T^I,\gamma _T^I)$ are in one-to-one correspondence with the elements of
$\mathit {SHI}(M_T^I,\gamma _T^I)$ are in one-to-one correspondence with the elements of ![]() $\mathfrak {S}(\mathcal {H})$, which will then complete the proof.
$\mathfrak {S}(\mathcal {H})$, which will then complete the proof.
For this claim, we consider the restriction of ![]() $\gamma _T^I$ to the ball
$\gamma _T^I$ to the ball ![]() $\mathbb {D}_{\alpha _i}$. Let
$\mathbb {D}_{\alpha _i}$. Let
denote the intersection points between ![]() $\alpha _i$ and
$\alpha _i$ and ![]() $\beta$. Then
$\beta$. Then ![]() $\gamma _T^I$ restricts to exactly one component on the boundary of
$\gamma _T^I$ restricts to exactly one component on the boundary of ![]() $\mathbb {D}_{\alpha _i}$ if and only if exactly one of
$\mathbb {D}_{\alpha _i}$ if and only if exactly one of ![]() $\epsilon _{\ell _1},\ldots \epsilon _{\ell _p}$ is
$\epsilon _{\ell _1},\ldots \epsilon _{\ell _p}$ is ![]() $-$ and the rest are
$-$ and the rest are ![]() $+$. The analogous statement holds for the restriction of
$+$. The analogous statement holds for the restriction of ![]() $\gamma _T^I$ to
$\gamma _T^I$ to ![]() $\mathbb {D}_{\beta _j}$. Thus, if we let
$\mathbb {D}_{\beta _j}$. Thus, if we let
then ![]() $\gamma _T^I$ restricts to exactly one component on each 3-ball in
$\gamma _T^I$ restricts to exactly one component on each 3-ball in ![]() $M_T^I$ if and only if
$M_T^I$ if and only if ![]() $q(I)\in \mathfrak {S}(\mathcal {H})$.
$q(I)\in \mathfrak {S}(\mathcal {H})$.
Remark 3.5 Proposition 3.1 also follows from the fact that ![]() $\mathit {SHI}$ and
$\mathit {SHI}$ and ![]() $\mathit {SFH}$ obey the same decomposition laws (Proposition 3.3, and the invariance under product disk decomposition), agree in rank for sutured 3-balls, and
$\mathit {SFH}$ obey the same decomposition laws (Proposition 3.3, and the invariance under product disk decomposition), agree in rank for sutured 3-balls, and
per Remark 3.2. Our original proof has the advantages that it does not rely on the definition of the differential in ![]() $\mathit {SFC}$, and it establishes a very concrete bijection between the nonzero summands
$\mathit {SFC}$, and it establishes a very concrete bijection between the nonzero summands ![]() $\mathit {SHI}(M_T^I,\gamma _T^I)$ and elements of
$\mathit {SHI}(M_T^I,\gamma _T^I)$ and elements of ![]() $\mathfrak {S}(\mathcal {H})$.
$\mathfrak {S}(\mathcal {H})$.
3.2 The proof
Recall that a sutured Heegaard diagram ![]() $\mathcal {H}$ for a balanced sutured manifold
$\mathcal {H}$ for a balanced sutured manifold ![]() $(M,\gamma )$ is admissible if and only if every nontrivial periodic domain has both positive and negative multiplicities [Reference JuhászJuh06]. This is automatically true of any
$(M,\gamma )$ is admissible if and only if every nontrivial periodic domain has both positive and negative multiplicities [Reference JuhászJuh06]. This is automatically true of any ![]() $\mathcal {H}$ when
$\mathcal {H}$ when ![]() $H_1(M,\partial M;\mathbb {Q})=0$ (there are no nontrivial periodic domains in this case), though every balanced sutured manifold admits an admissible diagram.
$H_1(M,\partial M;\mathbb {Q})=0$ (there are no nontrivial periodic domains in this case), though every balanced sutured manifold admits an admissible diagram.
Proof of Theorem 1.1 Let ![]() $\mathcal {H} = (\Sigma,\alpha,\beta )$ be an admissible sutured Heegaard diagram for
$\mathcal {H} = (\Sigma,\alpha,\beta )$ be an admissible sutured Heegaard diagram for ![]() $(M,\gamma )$. Then we can assign a positive integer area
$(M,\gamma )$. Then we can assign a positive integer area ![]() $a_i$ to each region
$a_i$ to each region ![]() $R_i$ of
$R_i$ of ![]() $\Sigma$–
$\Sigma$–![]() $\alpha$–
$\alpha$–![]() $\beta$ disjoint from
$\beta$ disjoint from ![]() $\partial \Sigma$, so that the signed area of every periodic domain is zero; see [Reference Ozsváth and SzabóOS04b, Lemma 4.12].Footnote 4 Fix
$\partial \Sigma$, so that the signed area of every periodic domain is zero; see [Reference Ozsváth and SzabóOS04b, Lemma 4.12].Footnote 4 Fix ![]() $a_i$ distinct points
$a_i$ distinct points ![]() $p_{i1},\ldots,p_{ia_i}\in R_i$ for each
$p_{i1},\ldots,p_{ia_i}\in R_i$ for each ![]() $i$, and let
$i$, and let
 \[ T = \bigcup_{i=1}^n\bigcup_{j=1}^{a_i} T_{ij} \subset M \]
\[ T = \bigcup_{i=1}^n\bigcup_{j=1}^{a_i} T_{ij} \subset M \]
be the corresponding full tangle for ![]() $\mathcal {H}$, as in § 3.1.
$\mathcal {H}$, as in § 3.1.
We claim that ![]() $[T]=0$ in
$[T]=0$ in ![]() $H_1(M,\partial M;\mathbb {Q})$. To see this, note that for every periodic domain
$H_1(M,\partial M;\mathbb {Q})$. To see this, note that for every periodic domain ![]() $P$ of
$P$ of ![]() $\mathcal {H}$, the intersection number of
$\mathcal {H}$, the intersection number of ![]() $T$ with the 2-cycle in
$T$ with the 2-cycle in ![]() $M$ represented by
$M$ represented by ![]() $P$ is negative the signed area of
$P$ is negative the signed area of ![]() $P$, which is zero. Since the homology classes represented by periodic domains span
$P$, which is zero. Since the homology classes represented by periodic domains span ![]() $H_2(M)$, the claim follows. Theorem 1.9 therefore implies that
$H_2(M)$, the claim follows. Theorem 1.9 therefore implies that
Theorem 1.1 then follows from the fact that
by Proposition 3.1.
Remark 3.6 It is not true that the inequality
holds for any sutured Heegaard diagram ![]() $\mathcal {H}$ for an arbitrary balanced sutured
$\mathcal {H}$ for an arbitrary balanced sutured ![]() $(M,\gamma )$. For example, consider the diagram
$(M,\gamma )$. For example, consider the diagram ![]() $\mathcal {H} = (T^2-D^2,\alpha _1,\beta _1)$ for
$\mathcal {H} = (T^2-D^2,\alpha _1,\beta _1)$ for
in which ![]() $\alpha _1$ and
$\alpha _1$ and ![]() $\beta _1$ are disjoint curves on the punctured torus. In this case, we know that
$\beta _1$ are disjoint curves on the punctured torus. In this case, we know that
while ![]() $|\mathfrak {S}(\mathcal {H})|=0$. The issue here is that
$|\mathfrak {S}(\mathcal {H})|=0$. The issue here is that ![]() $\mathcal {H}$ is not admissible.
$\mathcal {H}$ is not admissible.
4. Further directions
Let ![]() $\mathcal {H}$ be an admissible sutured Heegaard diagram for a balanced sutured manifold
$\mathcal {H}$ be an admissible sutured Heegaard diagram for a balanced sutured manifold ![]() $(M,\gamma )$. Let
$(M,\gamma )$. Let ![]() $T$ be a full tangle for
$T$ be a full tangle for ![]() $\mathcal {H}$, as defined in § 3. In ongoing work, we prove that
$\mathcal {H}$, as defined in § 3. In ongoing work, we prove that
has a basis given by the contact invariants of the tight contact structures on ![]() $(M_T,\gamma _T)$. In particular, this sutured instanton homology group is naturally graded by homotopy classes of 2-plane fields. We discuss potential applications of this fact in the following.
$(M_T,\gamma _T)$. In particular, this sutured instanton homology group is naturally graded by homotopy classes of 2-plane fields. We discuss potential applications of this fact in the following.
Let ![]() $T'$ be a mixed tangle for
$T'$ be a mixed tangle for ![]() $T$, as defined in § 2. Let
$T$, as defined in § 2. Let ![]() $V_{T}$ and
$V_{T}$ and ![]() $V_m$ be the groups
$V_m$ be the groups
from § 2, for ![]() $m\in \mathbb {N}$. To prove Theorem 1.1, we proved that
$m\in \mathbb {N}$. To prove Theorem 1.1, we proved that ![]() $V_T\cong \mathit {SHI}(-M_T,-\gamma _T)$ and
$V_T\cong \mathit {SHI}(-M_T,-\gamma _T)$ and
for sufficiently large ![]() $m$. However, in fact, this inequality can be viewed as coming from a spectral sequence similar to that in [Reference Li and YeLY22, § 4]. This spectral sequence can also be described as follows. From the bypass exact triangle used in § 2, we have that
$m$. However, in fact, this inequality can be viewed as coming from a spectral sequence similar to that in [Reference Li and YeLY22, § 4]. This spectral sequence can also be described as follows. From the bypass exact triangle used in § 2, we have that
where ![]() $\psi _-$ is the map associated to the bypass attachment along the arc
$\psi _-$ is the map associated to the bypass attachment along the arc ![]() $\eta _-$. One can prove, on the other hand, that
$\eta _-$. One can prove, on the other hand, that
for ![]() $m$ large, where
$m$ large, where ![]() $\psi _+$ is a related bypass attachment map. The groups
$\psi _+$ is a related bypass attachment map. The groups ![]() $V_m$ and
$V_m$ and ![]() $V_{m+1}$ can be graded using the rational Seifert surface for
$V_{m+1}$ can be graded using the rational Seifert surface for ![]() $T'$, as in [Reference LiLi21]. After adjusting this grading by an overall shift, the map
$T'$, as in [Reference LiLi21]. After adjusting this grading by an overall shift, the map ![]() $\psi _-$ is grading-preserving while
$\psi _-$ is grading-preserving while ![]() $\psi _+$ decreases the grading by
$\psi _+$ decreases the grading by ![]() $1$, for
$1$, for ![]() $m$ large. The complex
$m$ large. The complex ![]() $\textrm {Cone}(\psi _--\psi _+)$ is then filtered, and the
$\textrm {Cone}(\psi _--\psi _+)$ is then filtered, and the ![]() $E_1$ page of the associated spectral sequence is
$E_1$ page of the associated spectral sequence is ![]() $H_*(\textrm {Cone}(\psi _-))$. In sum, we have a spectral sequence
$H_*(\textrm {Cone}(\psi _-))$. In sum, we have a spectral sequence
The first potential application of these ideas involves defining a grading on ![]() $\mathit {SHI}(-M,-\gamma )$ by homotopy classes of plane fields. Indeed,
$\mathit {SHI}(-M,-\gamma )$ by homotopy classes of plane fields. Indeed, ![]() $\mathit {SHI}(-M_T,-\gamma _T)$ has such a grading, as mentioned previously, as it is generated by contact invariants of contact structures. The manifold
$\mathit {SHI}(-M_T,-\gamma _T)$ has such a grading, as mentioned previously, as it is generated by contact invariants of contact structures. The manifold ![]() $(M_{T'},\gamma _{T'})$ is obtained by gluing
$(M_{T'},\gamma _{T'})$ is obtained by gluing ![]() $(M_T,\gamma _T)$ along annuli, as in § 2, and we believe that the tight contact structures on the latter glue to give tight contact structures on the former whose invariants form a basis for
$(M_T,\gamma _T)$ along annuli, as in § 2, and we believe that the tight contact structures on the latter glue to give tight contact structures on the former whose invariants form a basis for ![]() $V_T$. Thus, there should be a natural grading by homotopy classes of 2-plane fields on
$V_T$. Thus, there should be a natural grading by homotopy classes of 2-plane fields on ![]() $V_T$ as well. The bypass maps
$V_T$ as well. The bypass maps ![]() $\psi _-,\psi _+$ are natural from a contact-geometric standpoint, and should therefore shift plane field gradings in a sensible way. We expect that one can then use the relation between
$\psi _-,\psi _+$ are natural from a contact-geometric standpoint, and should therefore shift plane field gradings in a sensible way. We expect that one can then use the relation between ![]() $V_T$ and
$V_T$ and ![]() $\textrm {Cone}(\psi _-)$ and the structure of the latter to define a plane field grading on
$\textrm {Cone}(\psi _-)$ and the structure of the latter to define a plane field grading on ![]() $\textrm {Cone}(\psi _-)$, and then on
$\textrm {Cone}(\psi _-)$, and then on ![]() $\textrm {Cone}(\psi _--\psi _+)$.
$\textrm {Cone}(\psi _--\psi _+)$.
A grading by homotopy classes of 2-plane fields on ![]() $\mathit {SHI}$ would enable one to define
$\mathit {SHI}$ would enable one to define ![]() $\textrm {Spin}^c$ decompositions of these groups, as well as an analogue of the Maslov grading in Heegaard Floer homology (see [Reference Li and YeLY22, § 4] for another approach to such a decomposition). The current lack of such structure makes it difficult to translate arguments from the Heegaard Floer setting to the instanton Floer setting.
$\textrm {Spin}^c$ decompositions of these groups, as well as an analogue of the Maslov grading in Heegaard Floer homology (see [Reference Li and YeLY22, § 4] for another approach to such a decomposition). The current lack of such structure makes it difficult to translate arguments from the Heegaard Floer setting to the instanton Floer setting.
A related second application is towards proving the isomorphism (1.1). Indeed, there is some hope that one could understand the spectral sequence (4.1) purely in terms of contact geometry, and thereby obtain a more axiomatic proof that
since the analogous spectral sequences can be defined in the Heegaard Floer and monopole Floer settings by the same contact-geometric means.
A more pedestrian approach to (4.2) is the following: first, prove that one can understand the spectral sequence
as coming from a differential
where ![]() $\partial _k$ shifts a grading (coming from homotopy classes of 2-plane fields) on
$\partial _k$ shifts a grading (coming from homotopy classes of 2-plane fields) on ![]() $\mathbb {C}^{|\mathfrak {S}(\mathcal {H})|}\cong V_T$ by
$\mathbb {C}^{|\mathfrak {S}(\mathcal {H})|}\cong V_T$ by ![]() $k$, such that
$k$, such that
Then, for generators ![]() $x,y\in \mathfrak {S}(\mathcal {H})$ and the corresponding basis elements
$x,y\in \mathfrak {S}(\mathcal {H})$ and the corresponding basis elements ![]() $e_x,e_y\in \mathbb {C}^{|\mathfrak {S}(\mathcal {H})|}$, perhaps one could use the 2-plane field gradings to show that the coefficient
$e_x,e_y\in \mathbb {C}^{|\mathfrak {S}(\mathcal {H})|}$, perhaps one could use the 2-plane field gradings to show that the coefficient
is nonzero only if there is a homotopy class of Whitney disks
with positive domain in ![]() $\mathcal {H}$ and Maslov index one. If even this were true, then one could prove, for example, that the inequality in Corollary 1.7 is an equality,
$\mathcal {H}$ and Maslov index one. If even this were true, then one could prove, for example, that the inequality in Corollary 1.7 is an equality,
for ![]() $(1,1)$-knots
$(1,1)$-knots ![]() $K\subset L(p,q)$.
$K\subset L(p,q)$.
More generally, the hope would be that for a nice diagram ![]() $\mathcal {H}$ (one in which the regions of
$\mathcal {H}$ (one in which the regions of ![]() $\Sigma$–
$\Sigma$–![]() $\alpha$–
$\alpha$–![]() $\beta$ disjoint from
$\beta$ disjoint from ![]() $\partial \Sigma$ are bigons or rectangles), one could show that the coefficient (4.3) is nonzero if and only if there is a class as in (4.4) with positive domain and Maslov index one (the domain of such a class is necessarily an empty embedded bigon or rectangle in this case). These are precisely the domains counted in the differential on
$\partial \Sigma$ are bigons or rectangles), one could show that the coefficient (4.3) is nonzero if and only if there is a class as in (4.4) with positive domain and Maslov index one (the domain of such a class is necessarily an empty embedded bigon or rectangle in this case). These are precisely the domains counted in the differential on ![]() $\mathit {SFC}(\mathcal {H})$ in this case, by [Reference Sarkar and WangSW10]. If one could further show that these domains are counted with the same nonzero complex coefficients in both the sutured instanton and Heegaard Floer settings, then this would prove (1.1) and then (4.2) by the same methods. If one could work with coefficients in
$\mathit {SFC}(\mathcal {H})$ in this case, by [Reference Sarkar and WangSW10]. If one could further show that these domains are counted with the same nonzero complex coefficients in both the sutured instanton and Heegaard Floer settings, then this would prove (1.1) and then (4.2) by the same methods. If one could work with coefficients in ![]() $\mathbb {F}=\mathbb {Z}/2\mathbb {Z}$, then the last step would be unnecessary, as all nonzero elements of this field are equal. Unfortunately,
$\mathbb {F}=\mathbb {Z}/2\mathbb {Z}$, then the last step would be unnecessary, as all nonzero elements of this field are equal. Unfortunately, ![]() $\mathit {SHI}$ is not defined over
$\mathit {SHI}$ is not defined over ![]() $\mathbb {F}$. On the other hand,
$\mathbb {F}$. On the other hand, ![]() $\mathit {SHM}$ is, and therefore the strategy outlined above minus the last step would be sufficient to give an alternative, more axiomatic proof that
$\mathit {SHM}$ is, and therefore the strategy outlined above minus the last step would be sufficient to give an alternative, more axiomatic proof that
Acknowledgements
We thank A. Levine, T. Lidman, S. Sivek, and J. Wang for interesting conversations, and the referee for helpful comments.
Conflicts of Interest
None.