Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-26T08:14:57.929Z Has data issue: false hasContentIssue false
  • English
  • Français

Symplectic quotients have symplectic singularities

Part of: General commutative ring theory Local rings and semilocal rings Linear algebraic groups and related topics Symplectic geometry, contact geometry

Published online by Cambridge University Press:  31 January 2020

Hans-Christian Herbig ,
Gerald W. Schwarz  and
Christopher Seaton
Hans-Christian Herbig
Affiliation:
Departamento de Matemática Aplicada, Universidade Federal do Rio de Janeiro, Av. Athos da Silveira Ramos 149, Centro de Tecnologia – Bloco C, CEP: 21941-909 Rio de Janeiro, Brazil email herbighc@gmail.com
Gerald W. Schwarz
Affiliation:
Department of Mathematics, Brandeis University, Waltham, MA02454-9110, USA email schwarz@brandeis.edu
Christopher Seaton
Affiliation:
Department of Mathematics and Computer Science, Rhodes College, 2000 N. Parkway, Memphis, TN38112, USA email seatonc@rhodes.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 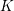$K$ be a compact Lie group with complexification 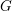$G$, and let 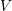$V$ be a unitary $K$-module. We consider the real symplectic quotient 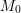$M_{0}$ at level zero of the homogeneous quadratic moment map as well as the complex symplectic quotient, defined here as the complexification of 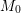$M_{0}$. We show that if 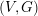$(V,G)$ is 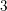$3$-large, a condition that holds generically, then the complex symplectic quotient has symplectic singularities and is graded Gorenstein. This implies in particular that the real symplectic quotient is graded Gorenstein. In case 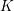$K$ is a torus or 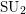$\operatorname{SU}_{2}$, we show that these results hold without the hypothesis that 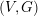$(V,G)$ is 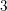$3$-large.

Keywords

singular symplectic reductionsymplectic singularitymoment mapHamiltonian actiongraded Gorenstein

MSC classification

Primary: 53D20: Momentum maps; symplectic reduction 13A50: Actions of groups on commutative rings; invariant theory
Secondary: 20G20: Linear algebraic groups over the reals, the complexes, the quaternions 57S15: Compact Lie groups of differentiable transformations 13H10: Special types (Cohen-Macaulay, Gorenstein, Buchsbaum, etc.)
Type
Research Article
Information
Compositio Mathematica , Volume 156 , Issue 3 , March 2020 , pp. 613 - 646
Copyright
© The Authors 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

C.S. was supported by the E.C. Ellett Professorship in Mathematics.

References

Arms, J. M., Gotay, M. J. and Jennings, G., Geometric and algebraic reduction for singular momentum maps, Adv. Math. 79 (1990), 43–103.CrossRefGoogle Scholar
Avramov, L. L., Complete intersections and symmetric algebras, J. Algebra 73 (1981), 248–263.CrossRefGoogle Scholar
Beauville, A., Symplectic singularities, Invent. Math. 139 (2000), 541–549.CrossRefGoogle Scholar
Becker, T., On the existence of symplectic resolutions of symplectic reductions, Math. Z. 265 (2010), 343–363.CrossRefGoogle Scholar
Benson, D. J., Polynomial invariants of finite groups, London Mathematical Society Lecture Note Series, vol. 190 (Cambridge University Press, Cambridge, 1993).CrossRefGoogle Scholar
Berndt, R., Representations of linear groups (Vieweg, Wiesbaden, 2007).Google Scholar
Bruns, W. and Herzog, J., Cohen-Macaulay rings, Cambridge Studies in Advanced Mathematics, vol. 39 (Cambridge University Press, Cambridge, 1993).Google Scholar
Bellamy, G. and Kuwabara, T., On deformation quantizations of hypertoric varieties, Pacific J. Math. 260 (2012), 89–127.CrossRefGoogle Scholar
Bulois, M., Lehn, C., Lehn, M. and Terpereau, R., Towards a symplectic version of the Chevalley restriction theorem, Compos. Math. 153 (2017), 647–666.CrossRefGoogle Scholar
Boutot, J.-F., Singularités rationnelles et quotients par les groupes réductifs, Invent. Math. 88 (1987), 65–68.CrossRefGoogle Scholar
Brylinski, R., Dixmier algebras for classical complex nilpotent orbits via Kraft–Procesi models. I, in The orbit method in geometry and physics (Marseille, 2000), Progress in Mathematics, vol. 213 (Birkhäuser, Boston, MA, 2003), 49–67.CrossRefGoogle Scholar
Bellamy, G. and Schedler, T., Symplectic resolutions of quiver varieties and character varieties, Preprint (2016), arXiv:1602.00164 [math.AG].Google Scholar
Bellamy, G. and Schedler, T., On symplectic resolutions and factoriality of Hamiltonian reductions, Math. Ann. 375 (2019), 165–176.CrossRefGoogle Scholar
Bulois, M., On the normality of the null-fiber of the moment map for 𝜃- and tori representations, J. Algebra 507 (2018), 502–524.CrossRefGoogle Scholar
Chevalley, C., Invariants of finite groups generated by reflections, Amer. J. Math. 77 (1955), 778–782.CrossRefGoogle Scholar
Cape, J., Herbig, H.-C. and Seaton, C., Symplectic reduction at zero angular momentum, J. Geom. Mech. 8 (2016), 13–34.Google Scholar
Cox, D. A., Little, J. B. and Schenck, H. K., Toric varieties, Graduate Studies in Mathematics, vol. 124 (American Mathematical Society, Providence, RI, 2011).CrossRefGoogle Scholar
Doran, B. and Hoskins, V., Algebraic symplectic analogues of additive quotients, J. Symplectic Geom. 16 (2018), 1591–1638.CrossRefGoogle Scholar
Derksen, H. and Kemper, G., Computational invariant theory, in Invariant theory and algebraic transformation groups, I, Encyclopaedia of Mathematical Sciences, vol. 130 (Springer, Berlin, 2002).Google Scholar
Drézet, J.-M., Luna’s slice theorem and applications, in Algebraic group actions and quotients (Hindawi, Cairo, 2004), 39–89.Google Scholar
Eisenbud, D., Commutative algebra, Graduate Texts in Mathematics, vol. 150 (Springer, New York, 1995).CrossRefGoogle Scholar
Farsi, C., Herbig, H.-C. and Seaton, C., On orbifold criteria for symplectic toric quotients, SIGMA Symmetry Integrability Geom. Methods Appl. 9 (2013), Paper 032, 18.Google Scholar
Fulton, W. and Lazarsfeld, R., Connectivity and its applications in algebraic geometry, in Algebraic geometry (Chicago, IL, 1980), Lecture Notes in Mathematics, vol. 862 (Springer, Berlin, 1981), 26–92.CrossRefGoogle Scholar
Flenner, H., Rationale quasihomogene Singularitäten, Arch. Math. (Basel) 36 (1981), 35–44.CrossRefGoogle Scholar
Flenner, H., Extendability of differential forms on nonisolated singularities, Invent. Math. 94 (1988), 317–326.CrossRefGoogle Scholar
Fu, B., Symplectic resolutions for nilpotent orbits, Invent. Math. 151 (2003), 167–186.CrossRefGoogle Scholar
Fu, B., A survey on symplectic singularities and symplectic resolutions, Ann. Math. Blaise Pascal 13 (2006), 209–236.CrossRefGoogle Scholar
Gordeev, N. L., Coranks of elements of linear groups and the complexity of algebras of invariants, Algebra i Analiz 2 (1990), 39–64; translation in Leningrad Math. J. 2(1991), 245–267.Google Scholar
Goresky, M. and MacPherson, R., Stratified Morse theory, Ergebnisse der Mathematik und ihrer Grenzgebiete (3) [Results in Mathematics and Related Areas (3)], vol. 14 (Springer, Berlin, 1988).CrossRefGoogle Scholar
Goto, S. and Watanabe, K., On graded rings. I, J. Math. Soc. Japan 30 (1978), 179–213.CrossRefGoogle Scholar
Hartshorne, R., Algebraic geometry, Graduate Texts in Mathematics, vol. 52 (Springer, Berlin, 1977).CrossRefGoogle Scholar
Herbig, H.-C., Herden, D. and Seaton, C., On compositions with x 2/(1 - x), Proc. Amer. Math. Soc. 143 (2015), 4583–4596.CrossRefGoogle Scholar
Herbig, H.-C., Iyengar, S. B. and Pflaum, M. J., On the existence of star products on quotient spaces of linear Hamiltonian torus actions, Lett. Math. Phys. 89 (2009), 101–113.CrossRefGoogle Scholar
Herbig, H.-C. and Schwarz, G. W., The Koszul complex of a moment map, J. Symplectic Geom. 11 (2013), 497–508.CrossRefGoogle Scholar
Herbig, H.-C. and Seaton, C., The Hilbert series of a linear symplectic circle quotient, Exp. Math. 23 (2014), 46–65.CrossRefGoogle Scholar
Herbig, H.-C. and Seaton, C., An impossibility theorem for linear symplectic circle quotients, Rep. Math. Phys. 75 (2015), 303–331.CrossRefGoogle Scholar
Herbig, H.-C., Schwarz, G. W. and Seaton, C., When is a symplectic quotient an orbifold?, Adv. Math. 280 (2015), 208–224.CrossRefGoogle Scholar
Huneke, C., Tight closure, parameter ideals, and geometry, in Six lectures on commutative algebra (Bellaterra, 1996), Progress in Mathematics, vol. 166 (Birkhäuser, Basel, 1998), 187–239.CrossRefGoogle Scholar
Huneke, C., Lectures on local cohomology, Interactions between homotopy theory and algebra, Contemporary Mathematics, vol. 436, 51–99 (American Mathematical Society, Providence, RI, 2007), Appendix 1 by Amelia Taylor.CrossRefGoogle Scholar
Ishii, S., Introduction to singularities (Springer, Tokyo, 2014).Google Scholar
Kaledin, D., Lehn, M. and Sorger, C., Singular symplectic moduli spaces, Invent. Math. 164 (2006), 591–614.CrossRefGoogle Scholar
Knop, F., Kraft, H. and Vust, T., The Picard group of a G-variety, in Algebraische Transformationsgruppen und Invariantentheorie, DMV Seminar, vol. 13 (Birkhäuser, Basel, 1989), 77–87.CrossRefGoogle Scholar
Kollár, J. and Mori, S., Birational geometry of algebraic varieties, Cambridge Tracts in Mathematics, vol. 134 (Cambridge University Press, Cambridge, 1998).CrossRefGoogle Scholar
Kraft, H. and Procesi, C., Closures of conjugacy classes of matrices are normal, Invent. Math. 53 (1979), 227–247.CrossRefGoogle Scholar
Kraft, H. and Procesi, C., On the geometry of conjugacy classes in classical groups, Comment. Math. Helv. 57 (1982), 539–602.CrossRefGoogle Scholar
Kraft, H. and Schwarz, G. W., Rational covariants or reductive groups and homaloidal polynomials, Math. Res. Lett. 8 (2001), 641–649.CrossRefGoogle Scholar
Luna, D., Sur les orbites fermées des groupes algébriques réductifs, Invent. Math. 16 (1972), 1–5.CrossRefGoogle Scholar
Luna, D., Slices étales, in Sur les groupes algébriques, Mémoires de la Société Mathématique de France, 33 (Société Mathématique de France, Paris, 1973), 81–105.Google Scholar
Luna, D., Adhérences d’orbite et invariants, Invent. Math. 29 (1975), 231–238.CrossRefGoogle Scholar
Luna, D. and Richardson, R. W., A generalization of the Chevalley restriction theorem, Duke Math. J. 46 (1979), 487–496.CrossRefGoogle Scholar
Luna, D. and Vust, Th., Un théorème sur les orbites affines des groupes algébriques semi-simples, Ann. Scuola Norm. Supér. Pisa (3) 27 (1973), 527–535; (1974).Google Scholar
Matsushima, Y., Espaces homogènes de Stein des groupes de Lie complexes, Nagoya Math. J 16 (1960), 205–218.CrossRefGoogle Scholar
Matsumura, H., Commutative ring theory, Cambridge Studies in Advanced Mathematics, vol. 8, second edition (Cambridge University Press, Cambridge, 1989), translated from the Japanese by M. Reid.Google Scholar
Namikawa, Y., Extension of 2-forms and symplectic varieties, J. Reine Angew. Math. 539 (2001), 123–147.Google Scholar
Panyushev, D. I., Rationality of singularities and the Gorenstein property of nilpotent orbits, Funktsional. Anal. i Prilozhen. 25 (1991), 76–78.CrossRefGoogle Scholar
Procesi, C. and Schwarz, G., Inequalities defining orbit spaces, Invent. Math. 81 (1985), 539–554.CrossRefGoogle Scholar
Popov, V. L. and Vinberg, È. B., Invariant theory, Algebraic geometry. IV Encyclopaedia of Mathematical Sciences, vol. 55 (Springer, Berlin, 1994).Google Scholar
Reid, M., Canonical 3-folds, in Journées de Géometrie Algébrique d’Angers, Juillet 1979/Algebraic Geometry, Angers, 1979 (Sijthoff & Noordhoff, Alphen aan den Rijn, 1980), 273–310.Google Scholar
Schwarz, G. W., Lifting smooth homotopies of orbit spaces, Publ. Math. Inst. Hautes Études Sci. 51 (1980), 37–135.CrossRefGoogle Scholar
Schwarz, G. W., The topology of algebraic quotients, in Topological methods in algebraic transformation groups (New Brunswick, NJ, 1988), Progress in Mathematics, vol. 80 (Birkhäuser, Boston, MA, 1989), 135–151.CrossRefGoogle Scholar
Schwarz, G. W., Lifting differential operators from orbit spaces, Ann. Sci. Éc. Norm. Supér (4) 28 (1995), 253–305.CrossRefGoogle Scholar
Grothendieck, A., Revêtements étales et groupe fondamental (SGA 1), Documents Mathématiques (Paris) (Société Mathématique de France, Paris, 2003); updated and annotated reprint of the 1971 original with two papers by M. Raynaud (Lecture Notes in Mathematics, vol. 224, Springer, Berlin).Google Scholar
Shephard, G. C. and Todd, J. A., Finite unitary reflection groups, Canad. J. Math. 6 (1954), 274–304.CrossRefGoogle Scholar
Sjamaar, R. and Lerman, E., Stratified symplectic spaces and reduction, Ann. of Math. (2) 134 (1991), 375–422.CrossRefGoogle Scholar
Stanley, R. P., Hilbert functions of graded algebras, Adv. Math. 28 (1978), 57–83.CrossRefGoogle Scholar
Stanley, R. P., Invariants of finite groups and their applications to combinatorics, Bull. Amer. Math. Soc. (N.S.) 1 (1979), 475–511.CrossRefGoogle Scholar
The Stacks Project Authors, Stacks Project, https://stacks.math.columbia.edu, 2018.Google Scholar
Starr, J., The homology groups of the smooth locus of a singular variety, https://mathoverflow.net/questions/309931/.Google Scholar
Terpereau, R., Schémas de Hilbert invariants et théorie classique des invariants, 2012, PhD thesis, Université de Grenoble.Google Scholar
Terpereau, R., Invariant Hilbert schemes and desingularizations of symplectic reductions for classical groups, Math. Z. 277 (2014), 339–359.CrossRefGoogle Scholar
van Leeuwen, M. A. A., Cohen, A. M. and Lisser, B., Lie, a package for Lie group computations, Computer Algebra Nederland, Amsterdam. Available at http://wwwmathlabo.univ-poitiers.fr/∼maavl/LiE/, 1992.Google Scholar
Verbitsky, M., Holomorphic symplectic geometry and orbifold singularities, Asian J. Math. 4 (2000), 553–563.CrossRefGoogle Scholar
Vinberg, È. B., Complexity of actions of reductive groups, Funktsional. Anal. i Prilozhen. 20 (1986), 1–13; 96.CrossRefGoogle Scholar
Watanabe, K., Certain invariant subrings are Gorenstein. I, II, Osaka J. Math. 11 (1974), 1–8; ibid. 11 (1974), 379–388.Google Scholar
Watanabe, K., Rational singularities with k ∗ -action, in Commutative algebra (Trento, 1981), Lecture Notes in Pure and Applied Mathematics, vol. 84 (Dekker, New York, 1983), 339–351.Google Scholar
Wehlau, D. L., A proof of the Popov conjecture for tori, Proc. Amer. Math. Soc. 114 (1992), 839–845.CrossRefGoogle Scholar
Weyl, H., The classical groups: their invariants and representations (Princeton University Press, Princeton, NJ, 1939.).Google Scholar
Wigner, E. P., Group theory and its application to the quantum mechanics of atomic spectra, Pure and Applied Physics, vol. 5, expanded and improved edition (Academic Press, New York, 1959), translated from the German by J. J. Griffin.Google Scholar