Tachikawa's second conjecture, derived recollements, and gendo-symmetric algebras

Abstract

Tachikawa's second conjecture for symmetric algebras is shown to be equivalent to indecomposable symmetric algebras not having any nontrivial stratifying ideals. The conjecture is also shown to be equivalent to the supremum of stratified ratios being less than 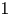$1$, when taken over all indecomposable symmetric algebras. An explicit construction provides a series of counterexamples to Tachikawa's second conjecture from each (potentially existing) gendo-symmetric algebra that is a counterexample to Nakayama's conjecture. The results are based on establishing recollements of derived categories and on constructing new series of algebras.

1. Introduction

In this section we first recall the Nakayama conjecture and Tachikawa's second conjecture, and then give an introductory description of our main results on Tachikawa's second conjecture for symmetric algebras, on constructions of mirror-reflective algebras, and on derived recollements and homological properties of these constructed algebras.

1.1 Homological conjectures and stratifying ideals

In the representation theory of algebras, the long-standing and not yet solved Nakayama conjecture says that a finite-dimensional algebra over a field with infinite dominant dimension is self-injective [Nak58]. This is one of the main homological conjectures in representation theory. It is equivalent to the combination of the following two conjectures by Tachikawa [Tac73, pp. 115–116].

1. (TC1) Let $\Lambda$ be a finite-dimensional algebra over a field $k$ and $D:={\rm Hom}_k(-,k)$. If ${\rm Ext}_\Lambda ^n(D(\Lambda ),\Lambda )=0$ for all $n\geq 1$, then $\Lambda$ is a self-injective algebra.

2. (TC2) Let $\Lambda$ be a finite-dimensional self-injective algebra over a field $k$ and $M$ a finitely generated $\Lambda$-module. Then $M$ is projective if it is self-orthogonal, that is, ${\rm Ext}_\Lambda ^n(M, M)=0$ for all $n\geq 1$.

In this paper we deal with (TC2) for symmetric algebras and show that (TC2) is closely related to stratifications of derived categories of algebras. Recall from [CPS96] that an ideal $AeA$ of an Artin algebra $A$ generated by an idempotent element $e\in A$ is called a stratifying ideal in $A$ if $Ae\otimes _{eAe}eA\simeq AeA$ and ${\rm Tor}_i^{eAe}(Ae,eA)=0$ for all $i>0$. In this case, the canonical surjection $\lambda : A\rightarrow A/AeA$ is a homological ring epimorphism, that is, the induced derived restriction functor from the derived category $\mathscr {D}(A/AeA)$ of $A/AeA$ to the derived category ${\mathscr D}(A)$ of $A$ is fully faithful, and therefore one has a recollement $(\mathscr {D}(A/AeA),\mathscr {D}(A),\mathscr {D}(eAe))$ of unbounded derived categories of algebras. Such a recollement of derived categories of algebras is called a standard recollement. Stratifying ideals are also termed strong idempotent ideals in [APT92] and homological ideals in [dlPX06]. Special examples of stratifying ideals are heredity ideals which play an important role in the study of quasi-hereditary algebras introduced in [CPS88]. A heredity ideal of an algebra $A$ is an ideal $I$ such that $I$ is idempotent (that is, $I^2=I$), $_AI$ is projective as an $A$-module and ${\rm End}_A(_AI)$ is semisimple.

An algebra $\Lambda$ is said to be derived simple if its derived module category ${\mathscr D}(\Lambda )$ admits no nontrivial recollements of derived module categories of algebras. Examples of derived simple algebras include local algebras, blocks of group algebras and some indecomposable algebras with two simple modules. One should not confuse the notion of derived simple algebras with that of $\mathscr {D}^{\rm b}({\rm mod})$-derived simple algebras in the sense that the bounded derived categories (of finitely generated modules) do not admit any nontrivial recollements of bounded derived categories of any algebras (see [LY12]). Derived simple algebras are $\mathscr {D}^{\rm b}({\rm mod})$-derived simple, but the converse is not true in general. By [LY12, Theorem 3.2], each indecomposable symmetric algebra is $\mathscr {D}^{\rm b}({\rm mod})$-derived simple.

Our first main result reads as follows.

Theorem 1.1 Let $k$ be a field.

1. (I) The following statements are equivalent.

   1. (1) Tachikawa's second conjecture holds for all symmetric $k$-algebras.

   2. (2) No indecomposable symmetric $k$-algebra has a stratifying ideal apart from itself and $0$.

2. (II) If each indecomposable symmetric $k$-algebra is derived simple, then Tachikawa's second conjecture holds for all symmetric $k$-algebras.

If an algebra $A$ has a nontrivial stratifying ideal generated by an idempotent element $e$, then there is a nontrivial recollement $({\mathscr D}(A/AeA),{\mathscr D}(A), {\mathscr D}(eAe))$. Thus, (II) follows from (I) immediately.

That (1) implies (2) follows from the following elementary observation. Assume that (TC2) holds for all symmetric algebras over $k$. Let $S$ be an indecomposable symmetric $k$-algebra and $I$ a stratifying ideal of $S$. Then $0={\rm Ext}_{S/I}^i(S/I, S/I)\simeq {\rm Ext}_S^i(S/I, S/I)$ for all $i\geq 1$. This means that ${_S}S/I$ is self-orthogonal. Then the $S$-module $S/I$ is projective by (1), and therefore ${_S}S\simeq I\oplus S/I$. It follows from $I^2=I$ that ${\rm Hom}_S(I, S/I)=0$. Since $S$ is symmetric and ${_S}I$ is projective, ${\rm Hom}_S(S/I, I)\simeq D\,{\rm Hom}_S(I, S/I)=0$. Consequently, $S\simeq {\rm End}_S(I)\oplus {\rm End}_S(S/I)$ as algebras. Since $S$ is indecomposable, either ${\rm End}_S(I)=0$ or ${\rm End}_S(S/I)=0$. In other words, $I=0$ or $I=S$. This implies that $S$ has no stratifying ideal apart from itself and $0$. So $(1)$ implies $(2)$.

Thus, the crucial part of Theorem 1.1(I) is to prove that (2) implies (1). Our proof is based on the new ideas and techniques to be discussed in the next subsection.

1.2 Derived recollements of gendo-symmetric algebras

In 1968, Müller investigated dominant dimensions of algebras and proved the following result in [Mul68]:

Let $\Lambda$ be a finite-dimensional $k$-algebra over a field $k$ and $M$ a finitely generated $\Lambda$-module. Then, for a nonnegative integer $n$, the dominant dimension of ${\rm End}_{\Lambda }(\Lambda \oplus D(\Lambda )\oplus M)$ is at least $n+2$ if and only if ${\rm Ext}^j_{\Lambda }(D(\Lambda )\oplus M,\Lambda \oplus M)=0$ for all $1\le j\le n$.

Thus, (TC2) holds for a self-injective algebra $\Lambda$ if and only if the Nakayama conjecture holds for the endomorphism algebras ${\rm End}_{\Lambda }(\Lambda \oplus M)$ for all finitely generated $\Lambda$-modules $M$. This suggests considering the algebras $A$ of the form ${\rm End}_{\Lambda }(\Lambda \oplus M)$ with $\Lambda$ a self-injective algebra and $M$ an arbitrary finitely generated $\Lambda$-module. Such algebras are called Morita algebras [KY13]. In the case that $\Lambda$ is symmetric, they are called gendo-symmetric algebras and studied in [FK11, CX16a, FK16]. In [CX22], self-orthogonal generators over a self-injective Artin algebra have been discussed systematically from the viewpoint of recollements of (relative) stable module categories. In particular, it is shown that the Nakayama conjecture holds true for Gorenstein–Morita algebras [CX22, Corollary 1.4].

To prove that (2) implies (1) in Theorem 1.1, we assume that there is a gendo-symmetric algebra which is a counterexample to Nakayama's conjecture. Then we have to find a nontrivial stratifying recollement, or a nontrivial stratifying ideal in some algebra related to the counterexample. This is based on an inductive construction of a series of new algebras. Roughly speaking, starting with a gendo-symmetric algebra $A$ and an idempotent element $e$ of $A$ such that the $A$-module $Ae$ is faithful and projective-injective, we construct four families of algebras inductively: $R_n$, $S_n$, $A_n$ and $B_n$ for $n\geq 1$ (see Section 5.3 for details). They are called the $n$th mirror-reflective, reduced mirror-reflective, gendo-symmetric and reduced gendo-symmetric algebras of $(A,e)$, respectively. These algebras are connected by derived recollements, as is shown in the next result. Here, ${\mathscr D}^-(A)$ and ${\mathscr D}(A)$ denote the bounded-above and unbounded derived categories of $A$, respectively, and domdim(A) stands for the dominant dimension of A.

Theorem 1.2 Let $(A,e)$ be a gendo-symmetric algebra and $n$ a positive integer. Then the following statements hold.

1. (1) There exist recollements of bounded-above derived categories of algebras induced by stratifying ideals:

   
   with $B_0:=(1-e)A(1-e)$.

2. (2) Let $R_0=S_0:=eAe$. If ${\rm domdim}(A)=\infty$, then there exist recollements of unbounded derived categories of algebras induced by stratifying ideals:

   

Thus, the dominant dimension of a gendo-symmetric algebra $A$ being infinite means that $A$ is a potential counterexample to Nakayama's conjecture. It is a counterexample if and only if the second recollement in Theorem 1.2(2) becomes nontrivial for some $n$ (or equivalently, for all $n$). In this case, the algebra $B_0\ne 0$. Hence, if (TC2) for symmetric algebras fails, that is, Nakayama's conjecture for gendo-symmetric algebras fails, then there are arbitrarily long nontrivial stratifying chains or recollements. This explicit construction produces a series of counterexamples provided there is at least one counterexample.

Motivated by Theorem 1.2(2), we introduce the stratified dimension of an algebra. This measures how many steps an algebra can be stratified by its nontrivial stratifying ideals (see Definition 4.7), or equivalently, the derived category of the algebra can be stratified by nontrivial standard recollements of derived module categories. We also define the stratified ratio of an algebra to be the ratio of its stratified dimension to the number of isomorphism classes of simple modules (see Definition 4.10). Note that the iteration procedure of constructing $A_n$, $B_n$, $R_n$ and $S_n$ gives standard recollements of derived module categories. The connection between ${\rm (TC2)}$ and stratified dimensions (ratios) of algebras reads as follows.

Theorem 1.3 Tachikawa's second conjecture holds for all symmetric algebras over a field $k$ if and only if the supremum of stratified ratios of all indecomposable symmetric algebras over $k$ is less than $1$.

1.3 Mirror-reflective algebras and their homological properties

We now briefly outline the construction of mirror-reflective algebras and their homological properties. The first step of the construction is given in a general context.

Let $A$ be an associative algebra over a commutative ring $k$, $e$ an idempotent element of $A$, and $\Lambda :=eAe$. For $\lambda \in Z(\Lambda )$, the center of the algebra $\Lambda$, we introduce an associative algebra $R(A,e,\lambda )$, called the mirror-reflective algebra of $A$ at level $(e,\lambda )$, which has the underlying $k$-module $A \oplus Ae\otimes _\Lambda eA$, such that $Ae\otimes _\Lambda eA$ is an ideal in $R(A,e,\lambda )$ (see Section 3.1 for details). The terminology ‘mirror-reflective’ can be justified by Example 3.10 in Section 3.2. Moreover, the $k$-submodule of $R(A,e,\lambda )$,

\begin{align*} S(A,e,\lambda):=(1-e)A(1-e)\oplus Ae\otimes_\Lambda eA, \end{align*}

is closed under the multiplication of $R(A,e,\lambda )$. This is a possibly nonunitary algebra. It is called the reduced mirror-reflective algebra of $A$ at level $(e, \lambda )$. It has fewer simple modules than $R(A,e,\lambda )$ does, that is, the number of simple modules is reduced. The specializations of $R(A,e,\lambda )$ and $S(A,e,\lambda )$ at $\lambda =e$ are called the mirror-reflective algebra and reduced mirror-reflective algebra of $A$ at $e$, denoted by $R(A,e)$ and $S(A,e)$, respectively. Moreover, $S(A,e)=e_0R(A,e)e_0$ for an idempotent element $e_0$ in $R(A,e)$.

Clearly, each $A$-module is an $R(A,e)$-module via the canonical surjective homomorphism $R(A,e)\to A$ of algebras. Conversely, each $R(A,e)$-module restricts to an $A$-module via the canonical inclusion from $A$ into $R(A,e)$. Remark that each module over $(1-e)A(1-e)$ can also be regarded as a module over $S(A,e)$. So we have two basic constructions associated with $(A,e)$:

\begin{align*} \mathcal{A}(A,e):={\rm End}_{R(A,e)}(R(A,e)\oplus A(1-e)),\quad \mathcal{B}(A,e):={\rm End}_{S(A,e)}(S(A,e)\oplus (1-e)A(1-e)). \end{align*}

Now assume that $A$ is a gendo-symmetric algebra over a field and $e$ is an idempotent element of $A$ such that $Ae$ is a faithful, projective-injective $A$-module. In this case, we write $(A, e)$ for the gendo-symmetric algebra $A$. If $e'$ is another idempotent element of $A$ such that $Ae'$ is a faithful, projective-injective $A$-module, then $R(A,e)\simeq R(A,e')$ as algebras (see Lemma 3.6(1)). Hence, up to isomorphism of algebras, we can write $R(A)$ for $R(A,e)$ without referring to $e$, and call it the mirror-reflective algebra of the gendo-symmetric algebra $A$.

An Artin algebra $B$ is called an $n$-Auslander algebra ($n\ge 0$) if ${\rm gldim}(B)\leq n+1\leq {\rm domdim}(B)$; or an $n$-minimal Auslander–Gorenstein algebra if ${\rm idim}({_B}B)\leq n+1\leq {\rm domdim}(B)$ (see [Aus71, Iya07, CK16, IS18]), where ${\rm gldim}(B)$, ${\rm domdim}(B)$ and ${\rm idim}(_BB)$ denote the global, dominant and left injective dimensions of the algebra $B$, respectively. Clearly, $n$-Auslander algebras are exactly $n$-minimal Auslander–Gorenstein algebras of finite global dimension (see § 2).

Theorem 1.4 Let $(A,e)$ be a gendo-symmetric algebra. Then:

1. (1) $R(A,e,\lambda )$ is a symmetric algebra for $\lambda$ in the center of $eAe$.

2. (2) $\min \{{\rm domdim}(\mathcal {A}(A,e)), {\rm domdim}(\mathcal {B}(A,e))\} \geq {\rm domdim}(A)+2$.

3. (3) Let $n$ be a positive integer. If $A$ is an $n$-Auslander (respectively, $n$-minimal Auslander–Gorenstein) algebra, then $\mathcal {A}(A,e)$ is a $(2n+3)$-Auslander (respectively, $(2n+3)$-minimal Auslander–Gorenstein) algebra.

Theorem 1.4(1) not only implies that $R_n$ and $S_n$ are symmetric algebras and that $A_n$ and $B_n$ are gendo-symmetric algebras, but also lays a basis for the inductive construction of the series of algebras $A_n$, $B_n$, $R_n$ and $S_n$ in Theorem 1.2, while Theorem 1.4(2) says that $A_n$ and $B_n$ have higher homological dimensions: ${\rm domdim}(A_{n+1})\geq {\rm domdim}(A_n)+2$ and ${\rm domdim}(B_{n+1})\geq {\rm domdim}(B_n)+2$. Thus, $2n\le {\rm domdim}(A)+2(n-1)\le \min \{{\rm domdim}(A_n),{\rm domdim}(B_n)\}$. For the finitistic dimensions and algebraic $K$-groups of these algebras, we refer to Corollary 5.10.

1.4 Outline of the paper

The paper is structured as follows. In § 2 we recall the definitions of dominant dimensions, gendo-symmetric algebras, higher Auslander and Auslander–Gorenstein algebras. In § 3 we introduce (reduced) mirror-reflective algebras by reflecting a left (or right) ideal generated by an idempotent element. Further, we describe explicitly the mirror-reflective algebras by quivers with relations for algebras themselves presented by quivers with relations. This description explains visually the terminology of mirror-reflective algebras. In § 4 we recall the definitions of recollements and stratifying ideals (or strong idempotent ideals in other terminology). Also, we present the definitions of stratified dimensions and ratios of algebras (see Definitions 4.7 and 4.10, respectively). We then construct derived recollements from mirror-reflective algebras. In § 5 we first show Theorems 1.4 and 1.2. This relies on the fact that mirror-reflective algebras of gendo-symmetric algebras at any levels are symmetric (see Proposition 5.2). By iteration of forming (reduced) mirror-reflective algebras from a gendo-symmetric algebra, a series of recollements of derived module categories is established. This not only gives proofs of Theorems 1.1 and 1.3, but also establishes a precise relation between the numbers of simple modules over different mirror-reflective algebras (see Corollary 5.10(2)–(3)). Moreover, this construction of mirror-reflective algebras provides a new method to produce a series of $n$-minimal Auslander–Gorenstein algebras.

2. Dominant dimensions and gendo-symmetric algebras

Let $k$ be a commutative ring. All algebras considered are associative $k$-algebras with identity.

Let $A$ be a $k$-algebra. We denote by $A\text {-Mod}$ the category of all left $A$-modules, and by $A\text {-mod}$ the full subcategory of $A\text {-Mod}$ consisting of finitely generated $A$-modules. The global dimension of $A$, denoted by ${\rm gldim}(A)$, is defined to be the supremum of projective dimensions of all $A$-modules. The finitistic dimension of $A$, denoted by ${\rm findim}(A)$, is defined to be the supremum of projective dimensions of those $A$-modules which have finite projective resolutions by finitely generated projective modules. The projective and injective dimensions of an $A$-module $M$ are denoted by ${\rm pdim}(_AM)$ and ${\rm idim}({_A}M)$, respectively. If $f:X\to Y$ and $g:Y\to Z$ are homomorphisms of $A$-modules, we write $fg$ for the composition of $f$ with $g$, and $(x)f$ for the image of $x\in X$ under $f$.

For an additive category $\mathcal {C}$, let ${\mathscr C}(\mathcal {C})$ denote the category of all complexes over $\mathcal {C}$ with chain maps, and ${\mathscr K}(\mathcal {C})$ the homotopy category of ${\mathscr C}(\mathcal {C})$. We denote by ${\mathscr C}^{\mathrm {b}}(\mathcal {C})$ and ${\mathscr K}^{\mathrm {b}}(\mathcal {C})$ the full subcategories of ${\mathscr C}(\mathcal {C})$ and ${\mathscr K}(\mathcal {C})$, respectively, consisting of bounded complexes over $\mathcal {C}$. When $\mathcal {C}$ is abelian, the (unbounded) derived category of $\mathcal {C}$ is denoted by ${\mathscr D}(\mathcal {C})$, which is the localization of ${\mathscr K}(\mathcal {C})$ at all quasi-isomorphisms. The full subcategory of ${\mathscr D}(\mathcal {C})$ consisting of bounded-above complexes over $\mathcal {C}$ is denoted by ${\mathscr D}^-(\mathcal {C})$. As usual, we simply write ${\mathscr K}(A)$ for ${\mathscr K}(A\text {-Mod})$, ${\mathscr D}(A)$ for ${\mathscr D}(A\text {-Mod})$, and ${\mathscr D}^-(A)$ for ${\mathscr D}^-(A\text {-Mod})$. Also, we identify $A\text {-Mod}$ with the full subcategory of ${\mathscr D}(A)$ consisting of all stalk complexes in degree $0$.

For an Artin algebra, we denote by $\#(A)$ the number of isomorphism classes of simple $A$-modules, and by $D$ the usual duality of an Artin algebra.

Now let $A$ be a finite-dimensional algebra over a field $k$.

Definition 2.1 The dominant dimension of an algebra $A$, denoted by ${\rm domdim}(A)$, is the maximal natural number $n$ or $\infty$ such that the first $n$ terms $I_0, I_1, \ldots, I_{n-1}$ in a minimal injective resolution $0\rightarrow {}_AA\rightarrow I_0\rightarrow I_1\rightarrow \cdots \rightarrow I_i\rightarrow \cdots$ of $A$ are projective.

A module $M\in A\text {-mod}$ is called a generator if $_AA\in {\rm add}(M)$; a cogenerator if $D(A_A)\in {\rm add}(M)$; or a generator-cogenerator if it is both a generator and a cogenerator. By [Mul68, Lemma 3], if $_AM$ is a generator-cogenerator, then ${\rm domdim}({\rm End}_A(M))=\sup \{n\in \mathbb {N}\mid {\rm Ext}_A^i(M,M)=0, 1\leq i\leq n\}+2$.

Algebras of the form ${\rm End}_A(A\oplus M)$ with $A$ an algebra and $M$ an $A$-module have the double centralizer property and have been studied for a long time. Following [FK16], such an algebra is called a gendo-symmetric algebra if $A$ is a symmetric algebra. If $A$ is symmetric, then so is $eAe$ for $e=e^2\in A$.

Lemma 2.2 [FK11, Theorem 3.2]

The following statements are equivalent for an algebra $A$ over a field.

1. (1) $A$ is a gendo-symmetric algebra.

2. (2) ${\rm domdim}(A)\geq 2$ and $D(Ae)\simeq eA$ as $eAe$-$A$-bimodules, where $e\in A$ is an idempotent element such that $Ae$ is a faithful projective-injective $A$-module.

3. (3) ${\rm Hom}_A(D(A),A)\simeq A$ as $A$-$A$-bimodules.

4. (4) $D(A)\otimes _AD(A)\simeq D(A)$ as $A$-$A$-bimodules.

In the rest of the paper, we write $(A, e)$ for a gendo-symmetric algebra with $e$ an idempotent element in $A$ such that $Ae$ is a faithful projective-injective $A$-module. The category ${\rm add}(Ae)$ coincides with the full subcategory of $A\text {-mod}$ consisting of projective-injective $A$-modules.

An algebra $A$ is called an Auslander algebra if ${\rm gldim}(A)\leq 2\leq {\rm domdim}(A)$. This is equivalent to saying that $A$ is the endomorphism algebra of an additive generator of a representation-finite algebra over a field (see [Aus71]). A generalization of Auslander algebras is the so-called $n$-Auslander algebras. Let $n$ be a positive integer. Following [Aus71, Iya07, IS18], $A$ is called an $n$-Auslander algebra if ${\rm gldim}(A)\leq n+1\leq {\rm domdim}(A)$; or an $n$-minimal Auslander–Gorenstein algebra if ${\rm idim}({_A}A)\leq n+1\leq {\rm domdim}(A)$. Clearly, $n$-Auslander algebras are $n$-minimal Auslander–Gorenstein, while $n$-minimal Auslander–Gorenstein algebras of finite global dimension are $n$-Auslander. Moreover, these algebras can be characterized in terms of left or right perpendicular categories. For $M\in A\text {-mod}$ and $m\in \mathbb {N}$, we define

\begin{gather*} {}^{\perp_{m}}M:=\{X\in A\text{-mod}\mid{\rm Ext}_A^i(X,M) = 0,\ 1\leq i\leq m\},\\ M^{\perp_m}:=\{X\in A\text{-mod}\mid{\rm Ext}_A^i(M,X) = 0,\ 1\leq i\leq m~\}. \end{gather*}

An $A$-module $N$ is said to be maximal $(n-1)$-orthogonal or $n$-cluster tilting if ${\rm add}(_AN)= {}^{\perp _{n-1}}N=N^{\perp _{n-1}}$. A generator-cogenerator $M\in A\text {-mod}$ is said to be $(n-1)$-ortho-symmetric or $n$-precluster tilting if ${\rm add}(_AM)\subseteq {}^{\perp _{n-1}}M=M^{\perp _{n-1}}$. The algebra $A$ is $n$-Auslander if and only if there are an algebra $\Lambda$ and a maximal $(n-1)$-orthogonal $\Lambda$-module ${_\Lambda }X$ such that $A={\rm End}_\Lambda (X)$ by [Iya07, Proposition 2.4.1], and is $n$-minimal Auslander–Gorenstein if and only if there are an algebra $\Lambda$ and an $(n-1)$-ortho-symmetric generator-cogenerator ${_\Lambda }X$ such that $A={\rm End}_\Lambda (X)$ by [IS18, Theorem 4.5] or [CK16, Corollary 3.18]. Moreover, by [IS18, Proposition 4.1], if $A$ is $n$-minimal Auslander–Gorenstein, then either $A$ is self-injective or ${\rm idim}({_A}A)=n+1={\rm domdim}(A)$. In the latter case, ${\rm idim}(A{_A})=n+1={\rm domdim}(A)$, and therefore $A$ is $(n+1)$-Gorenstein.

An $A$-module $M$ is said to be $m$-rigid if ${\rm Ext}_A^i(M,M)=0$ for all $1\leq i\leq m$. Over symmetric algebras, ortho-symmetric modules have been characterized as follows.

Lemma 2.3 [CK16, Corollary 5.4]

Let $A$ be a symmetric algebra and $N$ a basic $A$-module without any nonzero projective direct summands. For a natural number $m$, the $A$-module $A\oplus N$ is $m$-ortho-symmetric if and only if $N$ is $m$-rigid and $\Omega _A^{m+2}(N)\cong N$.

3. Mirror-reflective algebras

In this section we introduce (reduced) mirror-reflective algebras and describe them explicitly by quivers with relations.

3.1 Definition of mirror-reflective algebras

Throughout this subsection, assume that $A$ is an algebra over a commutative ring $k$. Let $M$ be an $A$-$A$-bimodule and $\alpha : {}_AM\otimes _AM\rightarrow M$ be a homomorphism of $A$-$A$-bimodules, such that the associative law holds:

(♡) \begin{equation*} ((x\otimes y)\alpha \otimes z)\alpha= (x\otimes (y \otimes z)\alpha)\alpha \quad \text{for } x,y,z\in M. \end{equation*}

We define a multiplication on the underlying abelian group $A\oplus M$ by setting

\begin{align*} (a, m)\cdot (b,n):= (ab, an+mb+(m\otimes n)\alpha)\quad \text{for } a,b\in A, \ m,n\in M. \end{align*}

Then $A\oplus M$ becomes an associative algebra with the identity $(1,0)$, denoted by $R(A,M,\alpha )$. In the following, we identify $A$ with $(A,0)$, and $M$ with $(0,M)$ in $R(A,M,\alpha )$. Thus, $A$ is a subalgebra of $R(A,M,\alpha )$ with the same identity, and $M$ is an ideal of $R(A,M,\alpha )$ such that $R(A,M,\alpha )/M\simeq A$.

We now consider a special case of the above construction. Let $e=e^2\in A$, $\Lambda :=eAe$ and $Z(\Lambda )$ be the center of $\Lambda$. For $\lambda \in Z(\Lambda )$, let $\omega _\lambda$ be the composition of the natural maps:

\begin{align*} (Ae\otimes_\Lambda eA)\otimes_A(Ae\otimes_\Lambda eA)&\stackrel{\simeq}{\longrightarrow}Ae\otimes_\Lambda (eA\otimes_AAe)\otimes_{\Lambda} eA \stackrel{\simeq}{\longrightarrow} Ae\otimes_\Lambda \Lambda\otimes_\Lambda eA\\ &\stackrel{{\rm Id}\otimes(\cdot\lambda)\otimes {\rm Id}}{\longrightarrow} Ae\otimes_\Lambda \Lambda\otimes_\Lambda eA\rightarrow Ae\otimes_\Lambda eA, \end{align*}

where $(\cdot \lambda ):\Lambda \to \Lambda$ is the multiplication map by $\lambda$. Then $\omega _{\lambda }$ satisfies the associative law (♡).

Let $R(A,e,\lambda ):=R(A, Ae\otimes _{\Lambda }eA,\omega _{\lambda })$. Then the elements of $R(A,e, \lambda )$ are of the form

\begin{align*} a+\sum_{i=1}^n a_ie\otimes eb_i \quad \text{for}\ a, a_i, b_i\in A,\ 1\leq i\leq n\in\mathbb{N}. \end{align*}

Multiplication, denoted by $\ast$, is explicitly given by

\begin{align*} (a + be\otimes ec)\ast (a' + b'e\otimes ec'):= aa' + (ab'e\otimes ec'+ be\otimes eca'+ becb'e\otimes\lambda ec') \end{align*}

for $a,b,c,a',b',c'\in A$, and can be extended linearly to elements of general form. In particular,

(♢) \begin{equation*} (ae\otimes eb)\ast(a'e\otimes eb')=aeba'e\lambda\otimes eb'=ae\otimes \lambda eba'e b'. \end{equation*}

Now consider the $k$-submodule $S(A,e,\lambda ):=(1-e)A(1-e)\oplus Ae\otimes _{\Lambda }eA$ of $R(A,e,\lambda )$. It can be checked that $S(A,e,\lambda )$ is closed under the multiplication of $R(A, e,\lambda )$. In general, $S(A,e,\lambda )$ may not have an identity. However, $S(A,e,e)$ has the identity $e_0: = (1-e) + e\otimes e$.

Definition 3.1 The algebra $R(A,e,\lambda )$ defined above is called the mirror-reflective algebra of $A$ at level $(e,\lambda )$. The algebra $S(A,e,\lambda )$ is called the reduced mirror-reflective algebra of $A$ at level $(e,\lambda )$.

The algebra $R(A,e,e)$ is then called the mirror-reflective algebra of $A$ at $e$, denoted by $R(A,e)$. The algebra $S(A,e,e)$ is called the reduced mirror-reflective algebra of $A$ at $e$, denoted by $S(A,e)$.

Compared with $R(A,e)$, $S(A,e)$ has fewer simple modules. So it is termed the reduced mirror-reflective algebra.

Example 3.2 Let $A$ be an algebra over a field $k$ presented by the quiver with a relation:

The composition $\alpha \beta$ of arrows $\alpha$ and $\beta$ means that $\alpha$ comes first and then $\beta$ follows. If $k$ is of characteristic $2$, then $A$ is just the Schur algebra $S(2,2)$. Let $e$ be the idempotent of $A$ corresponding to the vertex $2$. Then $R(A, e)$ is isomorphic to the algebra presented by the following quiver with relations:

The algebra $S(A, e)$ is isomorphic to the algebra presented by the quiver with relations:

A general description of mirror-reflective algebras presented by quivers with relations will be given in Section 3.2.

The following lemma is obvious.

Lemma 3.3

1. (1) $R(A,e,\lambda )/(Ae\otimes _\Lambda eA)\simeq A$ as algebras.

2. (2) If $\mu \in Z(\Lambda )$ is an invertible element, then $R(A,e,\lambda )\simeq R(A,e,\lambda \mu )$ as algebras.

For simplicity, let $R:=R(A,e)$, $S:=S(A,e)$ and $\bar {e}:=e\otimes e\in R$. Then $\bar {e}=\bar {e}^2$, $e\bar {e}=\bar {e}=\bar {e}e$, and $\{\bar {e}, e-\bar {e}, 1-e\}$ is a set of pairwise orthogonal idempotent elements in $R$. We define

\begin{align*} \pi_1: R\longrightarrow A,\quad a+\sum_{i=1}^n a_i\bar{e}b_i\mapsto a, \quad \text{and}\quad \pi_2: R\longrightarrow A,\quad a+\sum_{i=1}^n a_i\bar{e}b_i\mapsto a+\sum_{i=1}^n a_ieb_i \end{align*}

for $a, a_i, b_i\in A$ and $1\leq i\leq n$. Then $\pi _1$ and $\pi _2$ are surjective homomorphisms of algebras. Let

\begin{align*} I:={\rm Ker}(\pi_1),\quad J:={\rm Ker}(\pi_2)\quad \text{and}\quad e_0:=(1-e)+\overline{e}\in R. \end{align*}

Lemma 3.4

1. (1) $I=R\bar {e}R$, $J=R(e-\bar {e})R$, $IJ=0=JI$, $I+J=ReR$ and $S=e_0Re_0$.

2. (2) As an $A$-$A$-bimodule, ${}_AR_A$ has two decompositions: $R=A\oplus I=A\oplus J$.

3. (3) The map $\phi : R\rightarrow R,$ defined by $a+\sum _{i=1}^n a_i\bar {e}b_i\mapsto a+\sum _{i=1}^n a_i(e-\bar {e})b_i$, is an automorphism of algebras with $\phi ^2={\rm Id}_R$, such that $\pi _2=\phi \pi _1$, and the restriction of $\phi$ to $I$ induces an isomorphism $I\to J$ of $A$-$A$-bimodules.

4. (4) Both $\pi _1$ and $\pi _2$ induce surjective homomorphisms of algebras

   \begin{align*} \pi_1': S\longrightarrow (1-e)A(1-e)\quad\text{and}\quad\pi_2':S\longrightarrow A, \end{align*}
   respectively. Moreover, ${\rm Ker}(\pi _1')=I$ and ${\rm Ker}(\pi _2')=(1-e)J(1-e)=J\cap S$.

Proof. (1) Clearly, $I=Ae\otimes _\Lambda eA=A\bar {e}A= R\bar {e}R$. Since $(e-\bar {e})\pi _2=0$, we have $e-\bar {e}\in {\rm Ker}(\pi _2)=J$ and $R(e-\bar {e})R\subseteq J$. Conversely, if $r:=a+\sum _{i=1}^n a_i\bar {e}b_i\in J$, then $a+\sum _{i=1}^n a_ieb_i=(r)\pi _2=0$, that is, $a=-\sum _{i=1}^n a_ieb_i$. Consequently, $r=-\sum _{i=1}^n a_ieb_i+\sum _{i=1}^n a_i\bar {e}b_i=-\sum _{i=1}^n a_i(e-\bar {e})b_i\in R(e-\bar {e})R$. Thus, $J=R(e-\bar {e})R=A(e-\bar {e})A$. Note that $I+J=R\bar {e}R+R(e-\bar {e})R=ReR$. For any $x,y, x', y'\in A$, since $(x\bar {e}y)(x'(e-\bar {e})y')=x\bar {e}yx'ey'-x\bar {e}yx'ey'=0$, we have $IJ=0$. Similarly, $(x'(e-\bar {e})y')(x\bar {e}y)=0$, and therefore $JI=0$. Since $I$ is an ideal of $R$ and $IJ=JI=0$, it follows that $S=e_0Re_0$.

(2) $R$ contains $A$ as a subalgebra with the same identity, and the composition of the inclusion $A\subseteq R$ with $\pi _i$, for $i=1,2$, is the identity map of $A$. Thus, $(2)$ follows.

(3) By $(2)$, $I\simeq R/A\simeq J$ as $A$-$A$-bimodules. More precisely, the isomorphism from $I$ to $J$ is given by

\begin{align*} \varphi': \; I\longrightarrow J,\quad \sum_{i=1}^n a_i\bar{e}b_i\mapsto \sum_{i=1}^n a_i (e-\bar{e})b_i. \end{align*}

Further, the map $\phi : R=A\oplus I\to R=A\oplus J$ is induced from $\varphi '$, and therefore is a well-defined isomorphism of $A$-$A$-bimodules. Moreover, $\phi$ preserves the multiplication of $R$ and $\phi ^2={\rm Id}_R$. Thus, $\phi$ is an automorphism of algebras. The equality $\pi _2=\phi \pi _1$ follows from the definitions of $\pi _1, \pi _2$ and $\phi$.

(4) By the left and right multiplications by $e_0$ of $\pi _1$ and $\pi _2$, we then get $(4)$ by $(1)$.

The annihilator of an $R$-module $M$ is defined as ${\rm Ann}_{R}(M):=\{r\in R\mid rM=0\}$. It is an ideal of $R$.

Lemma 3.5

1. (1) If the right $A$-module $eA_{A}$ is faithful, then $J={\rm Ann}_{R^{\rm op}}(I)$. Dually, if $_{A}Ae$ is faithful, then $J={\rm Ann}_R(I)$.

2. (2) $\pi _2$ induces isomorphisms of abelian groups,

   \begin{align*} R\bar{e}\stackrel{\simeq}{\longrightarrow} Ae,\quad \bar{e}R\stackrel{\simeq}{\longrightarrow}eA \quad \text{and} \quad \bar{e}R\bar{e}\stackrel{\simeq}{\longrightarrow}eAe, \end{align*}
   while the map $\pi _2':S\to A$ in Lemma 3.4(4) induces isomorphisms of abelian groups,
   \begin{align*} S\bar{e}\stackrel{\simeq}{\longrightarrow} Ae,\quad \bar{e}S\stackrel{\simeq}{\longrightarrow}eA \quad \text{and} \quad \bar{e}S\bar{e}\stackrel{\simeq}{\longrightarrow}eAe. \end{align*}

3. (3) $\pi _1$ induces isomorphisms of abelian groups:

   \begin{align*} R(e-\bar{e})\stackrel{\simeq}{\longrightarrow} Ae,\quad (e-\bar{e})R\stackrel{\simeq}{\longrightarrow}eA \quad \text{and}\quad (e-\bar{e})R(e-\bar{e})\stackrel{\simeq}{\longrightarrow}eAe. \end{align*}

Proof. (1) Clearly, $J\subseteq {\rm Ann}_{R^{\rm op}}(I)$. This is due to $IJ=0$ by Lemma 3.4(1). We show $J\supseteq {\rm Ann}_{R^{\rm op}}(I)$. In fact, since $J={\rm Ker}(\pi _2)$, it suffices to prove that $(x)\pi _2=0$ for $x\in {\rm Ann}_{R^{\rm op}}(I)$. Let $y:=(x)\pi _2$. It follows from $Ix=0$ that $0=(Ix)\pi _2=(I)\pi _2 y=AeAy$. This implies $eAy=0$. Since $eA_{A}$ is faithful, we must have $y=0$, and therefore $x\in {\rm Ker}(\pi _2)=J$. Thus, $J={\rm Ann}_{R^{\rm op}}(I)$. We show the second identity similarly.

(2) Due to $(\bar {e})\pi _2=e$, the restriction $f_2: R\bar {e}\to Ae$ of $\pi _2$ to $R\bar {e}$ is surjective. As ${\rm Ker}(f_2)=R\bar {e}\cap J\subseteq JI=0$ by Lemma 3.4(1), $f_2$ is an isomorphism. Dually, the restriction $\bar {e}R\to eA$ of $\pi _2$ to $\bar {e}R$ is also an isomorphism. Consequently, $\pi _2$ induces an isomorphism of algebras from $\bar {e}R\bar {e}$ to $eAe$.

Since $IJ=JI=0$ by Lemma 3.4(1), we have $S\overline {e}=R\overline {e}$ and $\overline {e}S=\overline {e}R$. Clearly, $\overline {e}S\overline {e}=\overline {e}R\overline {e}$. Thus, the second statement in (2) holds.

(3) This follows from (2) and Lemma 3.4(3)–(4).

Consequently, Lemmas 3.4(1) and 3.5(2) imply that $\#(R)=\#(A)+\#(eAe)$.

To discuss the decomposition of $R$ as an algebra and to lift algebra homomorphisms, we show the following result. For a homomorphism $\alpha : A\to \Gamma$ of algebras, denote by ${\rm Hom}_{\alpha \text {-}{\rm Alg}}(R,\Gamma )$ the set of all algebra homomorphisms $\beta : R\to \Gamma$ such that the restriction of $\beta$ to $A$ coincides with $\alpha$.

Lemma 3.6

1. (1) If $u=u^2\in A$ such that ${\rm add}({_A}Au)={\rm add}({_A}Ae)$, then $R\simeq R(A,u,u)$ as algebras.

2. (2) If ${_A}Ae$ is a generator, then $R\simeq A\times A$ as algebras.

3. (3) Let $\alpha :A\to \Gamma$ be a homomorphism of algebras and define $f:=(e)\alpha$. Then there is a bijection

   \begin{align*} {\rm Hom}_{\alpha\text{-}{\rm Alg}}(R,\Gamma)\stackrel{\simeq}{\longrightarrow}\{x\in f\Gamma f \mid x^2=x, (c)\alpha\, x=x (c)\alpha\ \text{for}\ c\in\Lambda\},\quad \overline{\alpha}\mapsto (\overline{e})\overline{\alpha}. \end{align*}

Proof. (1) Let $U:=uAu$ and $\mathbf {P}_1(Ae)$ be the full subcategory of $A\text {-Mod}$ consisting of all modules $X$ such that there is an exact sequence $P_1\to P_0\to X\to 0$ of $A$-modules with $P_0, P_1 \in {\rm Add}(Ae)$, where ${\rm Add}(Ae)$ is the full subcategory of $A\text {-Mod}$ consisting of direct summands of direct sums of copies of $Ae$. We identify the functor ${\rm Hom}_A(Au,-): A\text {-Mod}\to U\text {-Mod}$ with the functor $u\cdot : A\text {-Mod}\to U\text {-Mod}$, given by the left multiplication of $u$. Let $\mu : Au\otimes _U u(-)\to {\rm Id}$ be the counit of the adjunction of the adjoint pair $(Au\otimes _U-, u\cdot )$. Then, for an $A$-module $X$, the map $\mu _X$ is an isomorphism if and only if $X\in \mathbf {P}_1(Au)$. Applying $Ae\otimes _{\Lambda }-$ to a projective presentation of ${_\Lambda }eA$, we obtain an exact sequence $P_1\to P_0\to Ae\otimes _{\Lambda }eA\to 0$ of $A$-modules with $P_1, P_0\in {\rm Add}(Ae)$. This shows $Ae\otimes _\Lambda eA\in \mathbf {P}_1(Ae)$. Due to ${\rm add}({_A}Au)={\rm add}({_A}Ae)$, we have $Ae\otimes _\Lambda eA\in \mathbf {P}_1(Au)$, and therefore $\mu _{Ae\otimes _\Lambda eA}: Au\otimes _U u(Ae\otimes _\Lambda eA)\to Ae\otimes _\Lambda eA$ is an isomorphism of $A$-$A$-modules. Since the multiplication map $\rho : Ae\otimes _\Lambda eA\to A, ae\otimes eb\mapsto aeb$ for $a, b\in A$, satisfies $e\,{\rm Ker}(\rho )=0=e\,{\rm Coker}(\rho )$, it follows from ${\rm add}({_A}Au)={\rm add}({_A}Ae)$ that $u\,{\rm Ker}(\rho )=0=u\,{\rm Coker}(\rho )$. Then $u\rho : u(Ae\otimes _\Lambda eA)\to uA$ is an isomorphism of $U$-$A$-bimodules, and $u\rho u: u(Ae\otimes _\Lambda eA)u\to uAu$ is an isomorphism of $U$-$U$-bimodules. Consequently, there is an isomorphism of $A$-$A$-bimodules

\begin{align*} \text{Id}_{Au}\otimes_U u\rho: \;Au\otimes_U u(Ae\otimes_\Lambda eA)\stackrel{\simeq}{\longrightarrow} Au\otimes_U uA. \end{align*}

Thus, $\psi :=(\text {Id}_{Au}\otimes _U u\rho )^{-1}\mu _{Ae\otimes _\Lambda eA}: Au\otimes _U uA\to Ae\otimes _\Lambda eA$ is an isomorphism of $A$-$A$-bimodules. In fact, if $x_i\in uAe$ and $y_i\in eAu$ with $1\leq i\leq n$ such that $\sum _{i=1}^nx_iy_i=u$, then $(a(u\otimes u)b)\psi =a(\sum _{i=1}^nx_i\otimes y_i)b$. This induces an isomorphism of $A$-$A$-bimodules:

\begin{gather*} {\rm Id}_A\oplus \psi: R(A,u,u)=A\oplus Au\otimes_U uA\longrightarrow R=A\oplus Ae\otimes_\Lambda eA,\\ (a, x\otimes y)\mapsto (a, (x\otimes y)\psi) \quad \text{for } a\in A,\ x\in Au,\ y\in uA. \end{gather*}

It can be verified that this is an isomorphism of algebras

(2) Suppose that ${_A}Ae$ is a generator. Then ${\rm add}(_AAe)={\rm add}(_AA)$. Let $B:=R(A,1,1)$. By $(1)$, $R\simeq B$ as algebras. Now, identifying $A\otimes _AA$ with $A$, we get $B=A\oplus A$ with multiplication given by

\begin{align*} (a_1,a_2)(b_1,b_2):=(a_1b_1, a_1b_2+a_2b_1+a_2b_2) \quad \text{for } a_1,a_2, b_1, b_2\in A. \end{align*}

Clearly, $(1,0)$ is the identity of $B$ and $(1,-1)$ is a central idempotent element of $B$. Thus, the map $B\to A\times A$, $(a_1,a_2)\mapsto (a_1, a_1+ a_2)$, is an algebra isomorphism. Thus, $R\simeq B\simeq A\times A$ as algebras.

(3) The algebra $\Gamma$ can be regarded as an $A$-$A$-bimodule via $\alpha$, and any $A$-$A$-bimodule can be considered as a module over the enveloping algebra $A^e:=A\otimes _kA^{^{\rm op}}$. Define $F=Ae\otimes _\Lambda -\otimes _\Lambda eA: \Lambda ^{e}\text {-Mod}\to A^{e}\text {-Mod}$ and $G=e(-)e: A^{e}\text {-Mod}\to \Lambda ^{e}\text {-Mod}$. Then there are isomorphisms of $k$-modules

\begin{align*} {\rm Hom}_{A^{\rm e}}(Ae\otimes_\Lambda eA, \Gamma)&\simeq{\rm Hom}_{A^e}(F(\Lambda), \Gamma)\simeq{\rm Hom}_{\Lambda^e}(\Lambda, G(\Gamma))={\rm Hom}_{\Lambda^e}(\Lambda, (e)\alpha\, \Gamma (e)\alpha)\\ &={\rm Hom}_{\Lambda^e}(\Lambda, f\Gamma f) =\{y\in f\Gamma f \mid (c)\alpha\,y =y (c)\alpha\ \text{for any}\ c\in\Lambda\}=:\Gamma'. \end{align*}

Let $\overline {\alpha }\in {\rm Hom}_{\alpha \text {-}{\rm Alg}}(R,\Gamma )$ and $x:=(\overline {e})\overline {\alpha }\in \Gamma$. Since the restriction of $\overline {\alpha }$ to $A$ equals $\alpha$, the restriction of $\overline {\alpha }$ to $Ae\otimes _\Lambda eA$ is an homomorphism of $A$-$A$-bimodules. By $\overline {e}^2=\overline {e}$, we have $x^2=x$ and $(ae\otimes eb)\overline {\alpha }=(a)\alpha \, x\, (b)\alpha$ for any $a,b\in A$. This means that $x\in \Gamma '$ and $\overline {\alpha }$ is determined by $\alpha$ and $x$. Thus, the map in (3) is well defined and injective.

Conversely, let $y\in \Gamma '$ and let $h: Ae\otimes _\Lambda eA\to \Gamma$ be the homomorphism of $A$-$A$-bimodules sending $ae\otimes eb$ to $(a)\alpha \, y (b)\alpha$. Define $\overline {h}:=(\alpha, h): R\to \Gamma$. Then $\overline {h}$ is an algebra homomorphism if and only if $((ae\otimes eb)\ast (a'e\otimes eb'))h=(ae\otimes eb)h(a'e\otimes eb')h$ for any $a, a', b, b'\in A$ if and only if $y(ba')\alpha \, y=(eba')\alpha \, y$ for any $b,a'\in A$. Now suppose $y^2=y$. Since $\alpha$ is an algebra homomorphism and $f y=y=y f$, we see that $(eba')\alpha \, y=(eba'e)\alpha \, y=(eba'e)\alpha \, y^2=y (eba'e)\alpha y=y (ba')\alpha \, y$. Thus, $\overline {h}$ is an algebra homomorphism with $y=(\overline {e})h=(\overline {e})\bar {h}$. This shows that the map in (3) is surjective. Hence, $(3)$ holds.

Proposition 3.7 Let $A$ be an indecomposable algebra. Then:

1. (1) $R$ is a decomposable algebra if and only if ${_A}Ae$ is a generator. In this case, $R\simeq A\times A$ as algebras.

2. (2) If ${\rm add}(Ae)\cap {\rm add}(A(1-e))=0$ and $(1-e)A(1-e)$ is an indecomposable algebra, then $S$ is an indecomposable algebra.

Proof. (1) If ${_A}Ae$ is a generator, then $R\simeq R(A,1,1)\simeq A\times A$ as algebras by Lemma 3.6(2), and therefore $R$ is decomposable. Conversely, assume that $R$ is a decomposable algebra. Then there is an element $z=z^2\in Z(R)$ of $R$ such that $z\neq 0,1$. Since $\pi _1:R\to A$ is a surjective homomorphism of algebras, it restricts to an algebra homomorphism $Z(R)\to Z(A)$. This implies $(z)\pi _1\in Z(A)$. Since $A$ is indecomposable, we have $(z)\pi _1=0$ or $1$. If $(z)\pi _1=0$, then $z\in {\rm Ker}(\pi _1)=I$. If $(z)\pi _1=1$, then $1-z\in I$. Similarly, by the surjective homomorphism $\pi _2$, we know $z\in J$ or $1-z\in J$. Assume $z\in I$. If $z\in J$, then $z=z^2\in IJ=0$ by Lemma 3.4(1). This is a contradiction. Thus, $1-z\in J$ and $1=z+(1-z)\in I+J=ReR$ by Lemma 3.4(1). This shows $ReR=R$. It then follows from $\pi _1$ that $AeA=A$. Hence, ${_A}Ae$ is a generator. For the case $1-z\in I$, we can show similarly that $_AAe$ is a generator.

(2) Let $J_1:=S\cap J$. In the proof of $(1)$, we replace $\pi _1$ and $\pi _2$ with $\pi _1': S\to (1-e)A(1-e)$ and $\pi _2': S\to A$ (see Lemma 3.4(4)), respectively, and show similarly that if $(1-e)A(1-e)$ is indecomposable and $S$ is decomposable, then $S=I+J_1$. In this case, the equality $A=AeA$ still holds because $\pi _2'$ is surjective with ${\rm Ker}(\pi _2')=J_1$ and $(\overline {e})\pi _2'=e$. Consequently, ${_A}Ae$ is a generator, and therefore the assumption ${\rm add}(Ae)\cap {\rm add}(A(1-e))=0$ forces $e=1$. Thus, $S=I\simeq A$ as algebras. This contradicts $A$ being indecomposable.

3.2 Examples of mirror-reflective algebras: quivers with relations

In this subsection we describe explicitly the mirror-reflective algebras for algebras presented by quivers with relations. This explains the terminology ‘mirror-reflective algebras’ (see Example 3.10 below).

Throughout this subsection we assume that $k$ is a field.

Let $Q:=(Q_0,Q_1)$ be a quiver with the vertex set $Q_0$ and arrow set $Q_1$. For an arrow $\alpha :i\to j$, we denote by $s(\alpha )$ and $t(\alpha )$ the starting vertex $i$ and the terminal vertex $j$, respectively. Composition of an arrow $\alpha : i\to j$ with an arrow $\beta : j\to m$ is written as $\alpha \beta$. A path of length $n\ge 0$ in $Q$ is a sequence $p:=\alpha _1\cdots \alpha _n$ of $n$ arrows $\alpha _i$ in $Q_1$ such that $t(\alpha _i)=s(\alpha _{i+1})$ for $1\leq i< n\in \mathbb {N}$. Set $s(p)=s(\alpha _1)$ and $t(p)=t(\alpha _n)$. In the case where $n=0$, we understand the trivial path as an vertex $i\in Q_0$, denoted by $e_i$, and set $s(e_i)=i=t(e_i)$. We write $\mathscr {P}(Q)$ for the set of all paths of finite length in $Q$. For a field $k$, we write $kQ$ for the path algebra of $Q$ over $k$. Clearly, it has $\mathscr {P}(Q)$ as a $k$-basis.

A relation $\sigma$ on $Q$ over $k$ is a $k$-linear combination of paths $p_i$ of length at least $2$. We may assume that all paths in a relation have the same starting vertex and terminal vertex, and define $s(\sigma )=s(p_i)$ and $t(\sigma )=t(p_i)$. If $\rho =\{\sigma _i\}_{i\in T}$ is a set of relations on $Q$ over $k$ with $T$ an index set, the pair $(Q,\rho )$ is called a quiver with relations over $k$. In this case, we have a $k$-algebra $k(Q,\rho ):=kQ/\langle \rho \rangle$, the quotient algebra of the path algebra $kQ$ modulo the ideal $\langle \rho \rangle$ generated by the relations $\sigma _i, i\in T$.

Lemma 3.8 Let $B$ be a $k$-algebra, $\{f_i\mid i\in Q_0\}$ a set of orthogonal idempotent elements in $B$ with $1_B=\sum _{i\in Q_0}f_i$, and $\{f_\alpha \mid \alpha \in Q_1\}$ a set of elements in $B$. If $f_{s(\alpha )}f_\alpha =f_\alpha =f_\alpha f_{t(\alpha )}$ for $\alpha \in Q_1$, then there is a unique algebra homomorphism $f: kQ\to B$ which sends $e_i\mapsto f_i$ and $\alpha \mapsto f_\alpha$ for $i\in Q_0$ and $\alpha \in Q_1$.

Let $Q':=(Q'_{0}, Q'_{1})$ be a full subquiver of $Q$, that is, $Q'_{0}\subseteq Q_0$ and $Q'_{1}=\{\alpha \in Q_1\mid s(\alpha ), t(\alpha )\in Q'_{0}\}$. Define

\begin{align*} A:=k(Q,\rho), \quad V_0:=Q_0\setminus Q'_{0} \quad \text{and}\quad e:=\sum_{i\in V_0}e_i\in A. \end{align*}

We shall explicitly describe the quiver and relations for the mirror-reflective algebra $R(A,e)$.

Let $\overline {Q}$ be a copy of the quiver $Q$, say $\overline {Q}_0=\{\bar {i}\mid i\in Q_0\}$ and $\overline {Q}_1=\{\bar {\alpha }\mid \alpha \in Q_1\}$, with $s(\bar {\alpha })=\bar {i}$ and $t(\bar {\alpha })=\bar {j}$ if $s(\alpha )=i$ and $t(\alpha )=j$. Consider $Q'$ as a full subquiver of $\overline {Q}$ by identifying $\bar {i}$ with $i$ for $i\in Q'_0$, and $\bar {\alpha }$ with $\alpha$ for $\alpha \in Q'_1$. So $Q_0\cap \overline {Q}_0=Q'_0$ and $Q_1\cap \overline {Q}_1 = Q'_1$. Let $\Delta :=(\Delta _0,\Delta _1)$ be the pullback of the quivers $Q$ and $\overline {Q}$ over $Q'$, that is,

\begin{align*} \Delta_0:= Q_0 \dot{\cup} (\overline{Q_{0}}\setminus Q'_0)\quad\text{and}\quad \Delta_1:=Q_1 \dot{\cup} (\overline{Q_1}\setminus Q'_{1}). \end{align*}

We define a map $(-)^+:\{e_i\mid i\in Q_0\}\cup Q_1\to k\Delta$ by

\begin{align*} e_i^+:=\left\{\begin{array}{@{}ll} e_i, & i\in Q'_{0},\\ e_i+e_{\overline{i}}, & i\in V_{0}, \end{array}\right. \quad \alpha^+:=\left\{\begin{array}{@{}ll} \alpha, & \alpha\in Q'_{1}, \\ \alpha+\overline{\alpha}, & \alpha\in Q_1\setminus Q'_{1}. \end{array}\right. \end{align*}

Since $e_{s(\alpha )}^+\alpha ^+=\alpha ^+=\alpha ^+e_{t(\alpha )}^+$ for any $\alpha \in Q_1$, it follows from Lemma 3.8 that $(-)^+$ can be extended to an algebra homomorphism

\begin{align*} (-)^+:\ kQ\longrightarrow k\Delta,\quad p\mapsto p^+:=\alpha_1^+\cdots\alpha_n^+ \quad \text{for } p=\alpha_1\cdots\alpha_n\in \mathscr{P}(Q). \end{align*}

Given a relation $\sigma :=\sum _{i=1}^na_ip_i$ on $Q$ with $a_i\in k$, $p_i\in \mathscr {P}(Q)$ for $1\leq i\leq n\in \mathbb {N}$, and $s(\sigma ), t(\sigma )\in Q'_{0}$, we define

\begin{align*} \sigma_+:=\sum_{1\le j\le n,\; p_j\in \mathscr{P}(Q')}a_jp_j +\sum_{1\le i\le n,\; p_i\notin\mathscr{P}(Q')}a_i(p_i+\overline{p_i})=\sigma + \sum_{1\le i\le n,\; p_i\notin\mathscr{P}(Q')}a_i\overline{p_i}. \end{align*}

Now let $\psi :=\psi _1\cup \psi _2\cup \psi _3\cup \psi _4$ with

\begin{align*} \psi_1 &:= \{\overline{a}p b, a p\overline{b} \mid a, b\in Q_1, s(a), t(b)\in V_{0}, p\in\mathscr{P}(Q'), apb\in\mathscr{P}(Q)\},\\ \psi_2 &:= \{\sigma\in\rho\mid s(\sigma)\in V_{0}\ \text{or}\ t(\sigma)\in V_{0}\},\\ \psi_3 &:= \{\overline{\sigma}\mid\sigma\in\psi_2\},\\ \psi_4 &:= \{\sigma_+\mid \sigma\in\rho, s(\sigma), t(\sigma)\in Q'_{0}\}. \end{align*}

Then $\psi$ is a set of relations on $\Delta$ over $k$, and we consider the $k$-algebra $k(\Delta, \psi )$.

Proposition 3.9

1. (1) The homomorphism $(-)^+:kQ\to k\Delta$ of algebras is injective and induces an injective homomorphism $\mu : A\to k(\Delta, \psi )$ of algebras.

2. (2) There exists an isomorphism $\theta : R(A,e)\stackrel {\simeq }{\longrightarrow } k(\Delta, \psi )$ of algebras such that $(e_i\otimes e_i)\theta =e_{\overline {i}}$ for $i\in V_0$, and the restriction of $\theta$ to $A$ coincides with $\mu$ in (1).

Proof. (1) For a subset $\mathcal {U}\subseteq k\Delta$, let $\langle \mathcal {U}\rangle$ be the ideal of $k\Delta$ generated by $\mathcal {U}$. Set $E:=\{e_{\overline {i}}\mid i\in V_{0}\}$ and denote by $\delta : k\Delta \to k\Delta /\langle E\rangle$ the canonical surjection. Then $k\Delta /\langle E\rangle \stackrel {\sim }{\longrightarrow } kQ$ as algebras and there are homomorphisms of algebras

\begin{align*} kQ\stackrel{(-)^+}{\longrightarrow}k\Delta\stackrel{\delta}{\longrightarrow}k\Delta/\langle E\rangle\stackrel{\sim}{\longrightarrow} kQ \end{align*}

such that their composition is the identity map of $kQ$. This shows that $(-)^+$ is injective. We define

\begin{align*} \rho^+:=\{\sigma^+\mid \sigma\in\rho\}\quad\text{and}\quad \psi':=\rho^+\cup\bigg(\bigcup_{i,j\in V_0 }(e_ik\Delta e_{\overline{j}}\cup e_{\overline{j}}k\Delta e_i)\bigg). \end{align*}

We shall show $\langle \psi '\rangle =\langle \psi \rangle$ in $k\Delta$.

In fact, let $\varphi = \bigcup _{i,j\in V_0 }(e_ik\Delta e_{\overline {j}}\cup e_{\overline {j}}k\Delta e_i)\subseteq \psi '$. Clearly, $\langle \varphi \rangle =\langle \psi _1\rangle$. Now consider the image of a path under $(-)^+$.

1. (i) For $p\in \mathscr {P}(Q)$ of length at least $1$, we have the following statements.

   1. (1) If $p\in \mathscr {P}(Q'),$ then $p^+=p$.

   2. (2) If $p\not \in \mathscr {P}(Q'),$ then $p^+=p+\overline {p}+ p'$ with $p'$ in the $k$-space $k\varphi$ generated by elements of $\varphi$.

2. (ii) For $\sigma \in \rho$, we write $\sigma = \sum _{i=1}^sa_ip_i + \sum _{j= s+1}^na_jp_j$ with $p_i$ a path in $kQ$ for $1\le i\le n$ such that $p_i\in \mathscr {P}(Q')$ for $1\le i\le s$ and $p_{j}\not \in \mathscr {P}(Q')$ for $s+1\le j\le n$. It follows from (i) that

   (*) \begin{align*} \sigma^+&=\sum_{i=1}^sa_ip^+_i + \sum_{j= s+1}^na_jp^+_j=\sum_{i=1}^sa_ip_i + \sum_{j= s+1}^na_j(p_j+\overline{p_j}+p'_j)\\ &=\sigma + \sum_{j=s+1}^na_j\overline{p_j}+ \sum_{j= s+1}^na_jp'_j. \end{align*}
   If $\sigma \in \psi _2$, then $s=0$ and $\sigma ^+=\sigma +\overline {\sigma }+ \sum _{j= 1}^na_jp'_j$ with $\overline {\sigma }\in \psi _3$, and therefore $\sigma ^+\in \langle \psi \rangle$. If $\sigma \not \in \psi _2$, that is, $s(\sigma ), t(\sigma )\in Q_0'$, then $\sigma _+\in \psi _4$ and $\sigma ^+=\sigma _+ + \sum _{j= s+1}^na_jp'_j\in \langle \psi \rangle$. Thus, $\langle \psi '\rangle \subseteq \langle \psi \rangle$ in $k\Delta$.

Conversely, pick up $\tau \in \psi$, we show $\tau \in \langle \psi '\rangle$. If $\tau =\sigma _+\in \psi _4$, then $\tau =\sigma ^+ - \sum _{j= s+1}^na_jp'_j\in \langle \psi '\rangle$. If $\tau = \sigma \in \psi _2$ and $s(\sigma )\in V_0$, then $e_{s(\sigma )}\overline {\sigma }=0$ and therefore $\sigma =e_{s(\sigma )}\sigma =e_{s(\sigma )}\sigma ^+-e_{s(\sigma )}\sum _{j=1}^na_jp'_j\in \langle \psi '\rangle$. If $\tau = \sigma \in \psi _2$ and $t(\sigma )\in V_0$, then $\overline {\sigma }e_{t(\sigma )}=0$ and $\sigma =\sigma e_{t(\sigma )}=\sigma ^+e_{t(\sigma )}-\sum _{j=1}^na_jp'_j e_{t(\sigma )} \in \langle \psi '\rangle$. If $\tau =\overline {\sigma }\in \psi _3$ with $\sigma \in \psi _2$, then $\overline {\sigma }=\sigma ^+-\sigma -\sum _{j= 1}^na_jp'_j$. By what we have just proved, $\sigma \in \langle \psi '\rangle$, and therefore $\overline {\sigma }\in \langle \psi '\rangle$. Thus, $\langle \psi \rangle \subseteq \langle \psi '\rangle,$ and therefore $\langle \psi '\rangle =\langle \psi \rangle$ and $k(\Delta,\psi ') = k(\Delta,\psi )$.

Since $\varphi \subseteq \langle E \rangle$, it is clear that $\langle \psi '\rangle \subseteq \langle \rho ^+\cup E\rangle$. By the third equality in (*) and the fact that $\sum _{j=s+1}^na_j\overline {p_j}$ and $\sum _{j= s+1}^na_jp'_j$ belong to $\langle E\rangle$, we obtain $\langle \rho ^+\cup E\rangle =\langle \rho \cup E\rangle$ in $k\Delta$. Thus, $k\Delta /\langle \rho ^+\cup E\rangle =k\Delta /\langle \rho \cup E\rangle \simeq kQ/\langle \rho \rangle = A$ as algebras. Moreover, since $\langle \rho ^+\rangle \subseteq \langle \psi '\rangle \subseteq \langle \rho ^+\cup E\rangle \subseteq k\Delta,$ the homomorphisms $(-)^+$ and $\delta$ induce algebra homomorphisms $\mu : A\to k\Delta /\langle \psi '\rangle$ and $\overline {\delta }: k\Delta /\langle \psi '\rangle \to k\Delta /\langle \rho ^+\cup E\rangle$, respectively. Now we identify $k\Delta /\langle \rho ^+\cup E\rangle$ with $A$. Then $\mu \overline {\delta }={\rm Id}_A$ and $\mu$ is injective.

(2) We first construct a map $\theta$ by applying Lemma 3.6(3). For simplicity, let

\begin{align*} R:=R(A,e),\quad S:=k(\Delta, \psi),\quad x:=\sum_{i\in V_0}e_{\overline{i}}\in S. \end{align*}

Then $x^2=x$. By $(1)$, $(e)\mu =e^+=\sum _{j\in V_0}(e_j+e_{\overline {j}})$. Since $e^+ e_{\overline {i}}=e_{\overline {i}}=e_{\overline {i}}e^+$, we have $e^+x=x=xe^+$ and $x\in e^+Se^+$. Recall that $e_jSe_{\overline {i}}=e_{\overline {i}}Se_j=0$ for $i,j\in V_0$, due to the relation set $\psi _1$. Thus, for $s\in S$, we have

\begin{gather*} e^+se^+x=e^+sx=\sum_{j\in V_0}\sum_{i\in V_0}(e_j+e_{\overline{j}})se_{\overline{i}}=\bigg(\sum_{j\in V_0}e_{\overline{j}}\bigg)s\bigg(\sum_{i\in V_0}e_{\overline{i}}\bigg),\\ x e^+se^+=xse^+=\sum_{i\in V_0}\sum_{j\in V_0}e_{\overline{i}}s(e_j+e_{\overline{j}})=\bigg(\sum_{i\in V_0}e_{\overline{i}}\bigg)s\bigg(\sum_{j\in V_0}e_{\overline{j}}\bigg). \end{gather*}

This shows $e^+se^+x=xe^+se^+$. Since $\Lambda =eAe$ and $(\Lambda )\mu \subseteq e^+Se^+$, we have $(c)\mu x=xe^+(c)\mu$ for any $c\in \Lambda$. By Lemma 3.6(3), there is a unique algebra homomorphism $\theta : R\to S$ such that the restriction of $\theta$ to $A$ equals $\mu$ and $(\overline {e})\theta =x$. Let $\overline {e_i}:=e_i\otimes e_i\in R$. Then $\overline {e_i}=e_i\overline {e}e_i$ and $(\overline {e_i})\theta =e_i^+x e_i^+= e_i^+(\sum _{i\in V_0}e_{\overline {i}})e_i^+ =e_{\overline {i}}$.

Next, we prove that $\theta$ is surjective. It suffices to show that $\Delta _1\subseteq {\rm Im}(\theta )$ and $e_t\in {\rm Im}(\theta )$ for $t\in \Delta _0$.

In fact, if $t\in Q'_{0}$, then $(e_t)\theta =(e_t)\mu =e_t$; if $t\in V_0$, then $(\overline {e_t})\theta =e_{\overline {t}}$ and $(e_t-{\overline {e_t}})\theta =e_t+e_{\overline {t}}-e_{\overline {t}}=e_t$. This implies that $e_t$ belongs to ${\rm Im}(\theta )$ for any $t\in \Delta _0$. Now let $\alpha : u\to v$ be an arrow in $Q_1$. If $u,v\in Q'_{0}$, then $(\alpha )\theta =\alpha$. If $u\in V_0$ or $v\in V_0$, then $(\alpha )\theta =(\alpha )\mu =\alpha +\overline {\alpha }$. In the case where $u\in V_0$, we get

\begin{align*} (\overline{e_u}\alpha)\theta=(\overline{e_u})\theta(\alpha)\theta =e_{\overline{u}}(\alpha)\mu=e_{\overline{u}}(\alpha+\overline{\alpha}) =\overline{\alpha}\quad\text{and}\quad (\alpha-\overline{e_u}\alpha)\theta=\alpha. \end{align*}

In the case where $v\in V_0$, we have $(\alpha \overline {e_v})\theta =\overline {\alpha }$ and $(\alpha -\alpha \overline {e_v})\theta =\alpha$. Thus, $Q_1\subseteq {\rm Im}(\theta )$ and $\overline {Q_1}\setminus Q'_{1}\subseteq {\rm Im}(\theta )$.

Finally, we construct an algebra homomorphism $\pi : S\to R$ such that $\theta \pi ={\rm Id}_R$, the identity map of $R$. This means that $\theta$ is injective. Hence, it is bijective.

We define a map $\{e_t\mid t\in \Delta _0\}\cup \Delta _1\to R$ by $e_i \mapsto e_i-\overline {e_i}$, $e_{\overline {i}}\mapsto \overline {e_i}$ for $i\in V_0$; $e_j\mapsto e_j$ for $j\in Q'_{0};$ and for $\alpha \in Q_1$,

\begin{align*} i\stackrel{\alpha}{\longrightarrow} j\mapsto \left\{\begin{array}{@{}ll} \alpha & i, j\in Q'_{0},\\ \alpha-\alpha \overline{e_j}, & i\in Q_0, j\in V_0,\\ \alpha-\overline{e_i}\alpha, & i\in V_0, j\in Q_0; \end{array}\right. \quad \overline{i}\stackrel{\overline{\alpha}}{\longrightarrow} \overline{j} \mapsto \left\{\begin{array}{@{}ll} \alpha \overline{e_j}, & i\in Q_0,\ j\in V_0,\\ \overline{e_i}\alpha, & i\in V_0,\ j\in Q_0. \end{array}\right. \end{align*}

Note that $\overline {e_i}\alpha =e_i\otimes \alpha =\alpha \otimes e_j=\alpha \overline {e_j}$ in $R$ for $i,j\in V_0$. By Lemma 3.8, the map can be extended to a unique homomorphism $\gamma : k\Delta \to R$ of algebras. Clearly, $\gamma$ preserves the idempotent elements corresponding to the vertices in $Q'_{0}$ and also the arrows in $Q'_{1}$. Further, if $i\in V_0$, then $(e_i^+)\gamma =(e_i+e_{\overline i})\gamma =e_i$; if $\alpha \in Q_1\setminus Q'_{1}$, then $(\alpha ^+)\gamma =(\alpha +\overline {\alpha })\gamma =\alpha$. This implies $(\sigma ^+)\gamma =\sigma$ for any $\sigma \in \rho$. Moreover, by Lemma 3.4(1),

\begin{align*} (e_ik\Delta e_{\overline{j}})\gamma\subseteq (e_i-\overline{e_i}) R\overline{e_j}\subseteq (e-\overline{e})R\overline{e}=0\quad \text{and}\quad (e_{\overline j}k\Delta e_i)\varphi\subseteq \overline{e_j} R(e_i-\overline{e_i})\subseteq \overline{e}R(e-\overline{e})=0 \end{align*}

for any $i,j\in V_0$. Consequently, we have $\langle \psi '\rangle \subseteq {\rm Ker}(\gamma )$, and therefore $\gamma$ induces an algebra homomorphism $\pi : S\to R$. Now let $g:=\theta \pi : R\to R$ and $h:=(-)^+\;\gamma : kQ\to R$. Since the restriction of $\theta$ to $A$ equals $\mu$, the restriction $g|_A: A\to R$ of $g$ to $A$ is induced from $h$. As $\gamma$ preserves the idempotent elements corresponding to the vertices in $Q_0$ and also the arrows in $Q_1$, we see that $g|_A$ has its image in $A$ and factorizes through ${\rm Id}_A$. Since $(\overline {e_i})g=(e_{\overline {i}})\pi =\overline {e_i}$ for $i\in V_0$ and $\overline {e}=\sum _{i\in V_0}\overline {e_i}$, we have $(\overline {e})g=\overline {e}$. Thus, $g={\rm Id}_R$ by Lemma 3.6(3).

Let us now illustrate the construction of $R(A,e)$ by an example.

Example 3.10 Suppose that $A$ is an algebra over a field $k$ presented by the quiver with relations:

Let $Q'$ be the full subquiver of $Q$ consisting of the vertex set $\{1,2,3\}$ and let $e=e_4+e_5$. By Proposition 3.9(2), the algebra $R(A, e)$ is isomorphic to the algebra presented by the following quiver with relations:

This quiver is the mirror reflection of that of $A$ along the full subquiver $Q'$ of $Q$.

4. Derived recollements

In this section we start by recalling recollements of triangulated categories, introduced by Beilinson, Bernstein and Deligne in [BBD82], and introduce the notion of stratified dimensions of algebras. We also construct recollements of mirror-reflective algebras.

4.1 Stratifying ideals and recollements

Definition 4.1 Let $\mathcal {T}$, $\mathcal {T'}$ and $\mathcal {T''}$ be triangulated categories. $\mathcal {T}$ admits a recollement of $\mathcal {T'}$ and $\mathcal {T''}$ (or there is a recollement among $\mathcal {T''}$, $\mathcal {T}$ and $\mathcal {T}'$) if there are six triangle functors

among the three categories such that the following four conditions are satisfied.

1. (1) $(i^*,i_*),(i_!,i^!),(j_!,j^!)$ and $(j^*,j_*)$ are adjoint pairs.

2. (2) $i_*,j_*$ and $j_!$ are fully faithful functors.

3. (3) $j^! i_!=0$ (and thus also $i^!j_*=0$ and $i^*j_!=0$).

4. (4) For an object $X\in \mathcal {T}$, there are triangles $i_!i^!(X)\to X\to j_*j^*(X)\to i_!i^!(X)[1]$ and $j_!j^!(X)\to X\to i_*i^*(X)\to j_!j^!(X)[1]$ induced by the counits and units of the adjunctions, where [$1$] is the shift functor of $\mathcal {T}$.

Recollements of derived module categories of rings are called derived recollements. Quasi-hereditary algebras, introduced by Cline, Parshall and Scott (see [CPS88, CPS96]), provide such a special class of derived recollements. For a heredity ideal $I$ of an algebra $A$ over a commutative ring, we have ${\rm Ext}_{A/I}^i(X,Y) \simeq {\rm Ext}_A^i(X,Y)$ for $(A/I)$-modules $X,Y$ and $i\ge 0$. A slight generalization of heredity ideals is the $n$-idempotent ideals defined in [APT92].

Definition 4.2 [APT92]

Let $A$ be an algebra, $I$ an ideal of $A$, and $n$ a positive integer. The ideal $I$ of $A$ is said to be $n$-idempotent if, for $X,Y\in (A/I)\text {-Mod}$, the canonical homomorphism ${\rm Ext}_{A/I}^i(X,Y) \to {\rm Ext}_A^i(X,Y)$ of $k$-modules is an isomorphism for all $1\leq i\leq n$.

The ideal $I$ is said to be a strong idempotent ideal if $I$ is $n$-idempotent for all $n\geq 1$. In this case, if $I=AeA$ for an idempotent element $e\in A$, then $e$ is called a strong idempotent element of $A$.

A strong idempotent ideal generated by an idempotent element is precisely a stratifying ideal as introduced in [CPS96, Definition 2.1.1]. We use the term ‘stratifying ideals’ throughout the paper. To emphasize the idempotent elements considered, we also retain the terminology of strong idempotent elements of algebras.

By a trivial strong idempotent element of $A$ we mean the idempotent element $0$ or an idempotent element $e$ with $AeA=A$. Clearly, an ideal $I$ is $1$-idempotent if and only if $I$ is idempotent. Moreover, stratifying ideals are closely related to homological ring epimorphisms. A ring homomorphism $\lambda :A\to B$ is called a homological ring epimorphism if the multiplication map $B\otimes _AB\to B$ is an isomorphism and ${\rm Tor}_i^A(B,B)=0$ for all $i\geq 1$. This is equivalent to saying that the derived restriction functor $D(\lambda _*):{\mathscr D}(B)\to {\mathscr D}(A)$, induced by the restriction functor $\lambda _*: B\text {-Mod}\to A\text {-Mod}$, is fully faithful. Note that an ideal $I$ of $A$ is a stratifying ideal if and only if the canonical surjection $A\to A/I$ is a homological ring epimorphism.

Lemma 4.3 [APT92]

Let $I=AeA$ for an idempotent element $e$ in $A$.

1. (1) Let $n$ be a positive integer. Then $I$ is $(n+1)$-idempotent if and only if the multiplication map

   \begin{align*} Ae\otimes_{eAe}eA\longrightarrow I, \quad ae\otimes eb\mapsto aeb,\quad a,b\in A \end{align*}
   is an isomorphism of $A$-$A$-bimodules and ${\rm Tor}_i^{eAe}(Ae,eA)=0$ for all $1\leq i\leq n-1$.

2. (2) If $I$ is $2$-idempotent, then

   \begin{align*} &\sup\{n\in\mathbb{N}\mid {\rm Ext}_A^i(A/I, A/I)=0, 1\leq i\leq n\}\\ &\quad\geq \sup\{n\in\mathbb{N}\mid{\rm Tor}_i^{eAe}(Ae,eA)=0, 1\leq i\leq n\}+2. \end{align*}

Proof. (1) Although all the results in [APT92] are stated for finitely generated modules over Artin algebras, many of them, such as Theorem 2.1, Lemma 3.1 and Propositions 2.4 and 3.7(b), hold for arbitrary modules over rings if we modify $\mathbf {P}_n$ in [APT92, Definition 2.3] as follows.

Let $\mathbf {P}_n(Ae)$ be the full subcategory of $A\text {-Mod}$ consisting of all modules $X$ such that there is an exact sequence $P_n\to \cdots \to P_1\to P_0\to X\to 0$ of $A$-modules with $P_i\in {\rm Add}(Ae)$ for $0\leq i\leq n$, where ${\rm Add}(Ae)$ is the full subcategory of $A\text {-Mod}$ consisting of direct summands of direct sums of copies of $Ae$.

By [APT92, Theorem 2.1], $I:=AeA$ is $(n+1)$-idempotent if and only if $I\in \mathbf {P}_n(Ae)$. In particular, $I$ is $2$-idempotent if and only if $I\in \mathbf {P}_1(Ae)$. By [APT92, Lemma 3.1], the adjoint pair $(Ae\otimes _{eAe}-, {\rm Hom}_A(Ae,-))$ between $(eAe)\text {-Mod}$ and $A\text {-Mod}$ induces additive equivalences between $(eAe)\text {-Mod}$ and $\mathbf {P}_1(Ae)$. Note that ${\rm Hom}_A(Ae, I)\simeq eI=eA$. Thus, $I\in \mathbf {P}_1(Ae)$ if and only if the multiplication map $Ae\otimes _{eAe}eA\to AeA$ is an isomorphism of $A$-$A$-bimodules. Assume now that $I$ is $2$-idempotent. By [APT92, Proposition 3.7(b)], $I\in \mathbf {P}_n(Ae)$ if and only if ${\rm Tor}_i^{eAe}(Ae, eA)=0$ for all $1\leq i< n$. This shows $(1)$.

(2) If $I$ is $(n+1)$-idempotent, then ${\rm Ext}_A^i(A/I, A/I)\simeq {\rm Ext}_{A/I}^i(A/I, A/I)=0$ for all $1\leq i\leq n+1$. Now $(2)$ follows from $(1)$.

Corollary 4.4

1. (1) Let $e$ and $f$ be idempotent elements of $A$ such that $ef=e=fe$. If $AeA$ is an $(n+1)$-idempotent ideal of $A$ for a positive integer $n$, then $fAeAf$ is an $(n+1)$-idempotent ideal of $fAf$. In particular, if $e$ is a strong idempotent element of $A$, then it is also a strong idempotent element of $fAf$.

2. (2) Let $\{e,e_1,e_2\}$ be a set of pairwise orthogonal idempotent elements of $A$ such that $e$ is a strong idempotent element of $A$. Define $f:=e+e_1$, $g:=e+e_1+e_2$ and $\overline {A}:=A/AeA$. Let $\overline {f}:=f+AeA$ denote the image of $f$ in $\overline {A}$. If $\overline {f}$ is a strong idempotent element of $\overline {g}\overline {A}\overline {g}$, then $f$ is a strong idempotent element of $gAg$.

Proof. (1) Transparently, $e\in fAf$, $efAfe=eAe$, $fAeAfe=fAe$ and $efAeAf=eAf$. If $Ae\otimes _{eAe}eA\simeq AeA$, then $fAe\otimes _{eAe}eAf\simeq fAeAf$. Since $Ae=fAe\oplus (1-f)Ae$ and $eA=eAf\oplus eA(1-f)$, we see that the abelian group ${\rm Tor}_i^{eAe}(fAe, eAf)$ is a direct summand of ${\rm Tor}_i^{eAe}(Ae, eA)$ for $i\in \mathbb {N}$. Then (1) follows from Lemma 4.3(1).

(2) Clearly, $AeA\subseteq AfA\subseteq AgA$, and $\overline {g}\overline {A}\overline {g}\simeq gAg/gAeAg$ and $\overline {g}\overline {A}\overline {g}/\overline {g}\overline {A}\overline {f}\overline {A}\overline {g}\simeq gAg/gAfAg$ as algebras. Suppose that $\overline {f}$ is a strong idempotent element of $\overline {g}\overline {A}\overline {g}$. Then the canonical surjection $\pi _2: gAg/gAeAg\to gAg/gAfAg$ is homological. Since $e$ is a strong idempotent element of $A$ and $ge=e=eg$, the canonical surjection $\pi _1: gAg\to gAg/gAeAg$ is also homological by (1). Observe that compositions of homological ring epimorphisms are again homological ring epimorphisms. Thus, $\pi _1\pi _2: gAg\to gAg/gAfAg$ is homological. This implies that $f$ is a strong idempotent element in $gAg$.

Let $e=e^2\in A$. If $AeA$ is a stratifying ideal in $A$, then the recollement of derived module categories of algebras,

is called a standard recollement induced by $AeA$. If ${_A}AeA$ or $AeA_A$ is projective (for example, $AeA$ is a heredity ideal in $A$), then $AeA$ is a stratifying ideal in $A$. In the case where ${_A}AeA$ is projective, the recollement restricts to a recollement $({\mathscr D}^-(A/AeA), {\mathscr D}^-(A), {\mathscr D}^-(eAe))$ of bounded-above derived categories.

For constructing finitely generated (one-sided) projective idempotent ideals of the endomorphism algebras of objects in additive categories (see [CX16b, Lemmas 3.2 and 3.4]), we have the following lemma.

Lemma 4.5 Suppose that $R$ is an algebra and $I$ is an ideal of $R$.

1. (1) Let $A:={\rm End}_R(R\oplus \; R/I)$ and $e^2=e\in A$ correspond to the direct summand $R/I$ of the $R$-module $R\oplus \; R/I$. Then $AeA{_A}$ is finitely generated and projective, and there is a recollement $({\mathscr D}(R/{\rm Ann}_{R^{\rm op}}(I)), {\mathscr D}(A), {\mathscr D}(R/I))$, with ${\rm Ann}_{R^{\rm op}}(I):=\{r\in R\mid Ir=0\}$.

2. (2) Let $B:={\rm End}_R(R\oplus I)$ and $f=f^2\in B$ correspond to the direct summand $I$ of the $R$-module $R\oplus I$. If $I$ is idempotent, then ${_B}BfB$ is finitely generated and projective, and there is a recollement $({\mathscr D}(R/I), {\mathscr D}(B), {\mathscr D}({\rm End}_R(I)))$.

Another way to produce finitely generated projective ideals comes from Morita context algebras, as explained below.

Let $R$ be an algebra and let $I$ and $J$ be ideals of $R$ with $IJ=0$. Define

\begin{align*} M_l(R,I,J):=\bigg(\begin{array}{@{}cc@{}} R & I\\ R/J & R/J \end{array}\bigg)\quad \bigg(\text{respectively,} \ M_r(R,I,J):=\bigg(\begin{array}{@{}cc@{}} R & R/I\\ J & R/I \end{array}\bigg)\bigg), \end{align*}

which is the Morita context algebra with the bimodule homomorphisms given by the canonical ones:

\begin{align*} I\otimes_{R/J}(R/J)\simeq I\hookrightarrow R,\quad (R/J)\otimes_R I\simeq I/JI\twoheadrightarrow (I+J)/J\hookrightarrow R/J \end{align*}

(respectively, $(R/I)\otimes _{R/I}J\simeq J\hookrightarrow R$, $J\otimes _R(R/I)\simeq J/JI\twoheadrightarrow (I+J)/I\hookrightarrow R/I$). Note that $M_r(R,I, {\rm Ann}_{R^{\rm op}}(I))\simeq {\rm End}_R(R\oplus R/I)$ as algebras. Moreover, if ${_R}R$ is injective and $I^2=I$, then $M_l(R,I,{\rm Ann}_{R^{\rm op}}(I))\simeq {\rm End}_R(R\oplus I)$ as algebras. This is due to ${\rm Hom}_R(I,R/I)=0$.

Let

\begin{align*} e:=\bigg(\begin{array}{@{}cc@{}} 0 & 0\\ 0 & 1+J \end{array}\bigg)\in M_l(R,I,J),\quad f:=\bigg(\begin{array}{@{}cc@{}} 0 & 0\\ 0 & 1+I \end{array}\bigg)\in M_r(R,I,J). \end{align*}

Then the next lemma is easy to verify.

Lemma 4.6 Let $A:=M_l(R,I,J)$ and $B:= M_r(R,I,J)$. Then ${_A}AeA$ and $BfB_B$ are finitely generated and projective. Moreover, there are recollements $({\mathscr D}(R/I), {\mathscr D}(A), {\mathscr D}(R/J))$ and $({\mathscr D}(R/J), {\mathscr D}(B), {\mathscr D}(R/I))$.

4.2 Stratified dimensions of algebras

Now, we introduce stratified dimensions of algebras over a commutative ring, which measure how many steps the given algebras can be stratified by their nontrivial strong idempotent elements.

Definition 4.7 By an idempotent stratification of length $n$ of an algebra $A$, we mean a set $\{e_i\mid 0\leq i\leq n\}$ of $n+1$ nonzero (not necessarily primitive) pairwise orthogonal idempotent elements of $A$ satisfying the following conditions:

1. (a) $1=\sum _{j=0}^{n}e_j$ and $e_{i+1}\notin Ae_{\leq i}A$ (or equivalently, $Ae_{\leq i}A \subsetneq Ae_{\leq (i+1)}A$) for all $0\leq i\leq n-1$, where $e_{\leq m}:=\sum _{j=0}^{m}e_j$ for $0\leq m\leq n$; and

2. (b) $e_{\leq i}$ is a strong idempotent element of the algebra $e_{\leq (i+1)}Ae_{\leq (i+1)}$ for $0\leq i\leq n-1$.

The stratified dimension of $A$, denoted by ${\rm stdim}(A)$, is defined to be the supremum of the lengths of all idempotent stratifications of $A$.

Clearly, ${\rm stdim}(A)=0$ if and only if $A$ has no stratifying ideal apart from itself and $0$. If ${\rm stdim}(A)=n>0$, then there are nontrivial standard recollements $({\mathscr D}(A_{i}/I_i),{\mathscr D}(A_i), {\mathscr D}(A_{i-1}))$, $1\leq i< n+1$, where $A_0:=e_0Ae_0$, $A_i:=e_{\leq i}Ae_{\leq i}$ and $I_i:=e_{\leq i}Ae_{\leq (i-1)}Ae_{\leq i}$ are as defined in Definition 4.7. Moreover, for any two algebras $\Gamma _1$ and $\Gamma _2$, ${\rm stdim}(\Gamma _1\times \Gamma _2)={\rm stdim}(\Gamma _1)+{\rm stdim}(\Gamma _2)+1$. This implies that the stratified dimension of the direct product of countably many copies of a field $k$ is infinite.

Stratifications of algebras in the sense of Cline, Parshall and Scott are idempotent stratifications. But the converse is not true. Following [CPS96, Chapter 2], a stratification of length $n+1$ of an algebra $A$ is a chain of ideals, $0=U_{-1}\subsetneq U_0\subsetneq U_1\subsetneq \cdots \subsetneq U_{n-1}\subsetneq U_n=A$, generated by idempotent elements such that $U_i/U_{i-1}$ is a stratifying ideal in $A/U_{i-1}$ for $0\leq i\leq n$. In this case, $A$ is said to be CPS stratified. If $\{e_i\mid 0\leq i\leq n\}$ is a complete set of nonzero primitive pairwise orthogonal idempotent elements of $A$ and $U_i=Ae_{\leq i}A$ for $0\leq i\leq n$, then $A$ is called a fully CPS-stratified algebra. Standardly stratified algebras with respect to an order of simple modules are fully CPS stratified.

Lemma 4.8 Let $\{e_i\mid 0\leq i\leq n\}$ be a set of nonzero pairwise orthogonal idempotent elements of $A$ satisfying condition (a) in Definition 4.7. Define $U_i:=Ae_{\leq i}A$ for $0\leq i\leq n$ and $U_{-1}:=0$. If $U_i/U_{i-1}$ is a stratifying ideal in $A/U_{i-1}$ for $0\leq i\leq n$, then condition (b) in Definition 4.7 holds.

Proof. Since $U_i/U_{i-1}$ is a stratifying ideal in $A/U_{i-1}$ by assumption, the canonical surjection $A/U_{i-1}\to A/U_i$ is homological. As the composition of homological ring epimorphisms is still a homological ring epimorphism, the canonical surjection $A\to A/U_i$ is homological. This implies that $e_{\leq i}$ is a strong idempotent element of $A$. By Corollary 4.4, $e_{\leq i}$ is a strong idempotent element of $e_{\leq (i+1)}Ae_{\leq (i+1)}$. Thus, Definition 4.7(b) holds.

Proposition 4.9 Let $A$ be an Artin algebra over a commutative Artin ring $k$. Then:

1. (1) ${\rm stdim}(A)\leq \#(A)-1$.

2. (2) If $A$ has a stratification of length $n+1$ with $n\in \mathbb {N}$, then ${\rm stdim}(A)\geq n$. In particular, if $A$ is a fully CPS-stratified algebra, then ${\rm stdim}(A)=\#(A)-1$.

3. (3) If ${\rm stdim}(A)\geq 1$, then ${\rm stdim}(A)=\sup _{e\in A}\{{\rm stdim}(eAe)+{\rm stdim}(A/AeA)+1\}$, where $e$ runs over all nonzero strong idempotent elements of $A$ with $AeA\neq A$.

4. (4) If $k$ is a field and $B$ is a finite-dimensional $k$-algebra, then

   \begin{align*} {\rm stdim}(A\otimes_kB)\geq ({\rm stdim}(A)+1)({\rm stdim}(B)+1)-1. \end{align*}

Proof. (1) This is clear by Definition 4.7(a).

(2) The first part of $(2)$ follows from Lemma 4.8. If $A$ is a fully CPS-stratified algebra, then it has a stratification of length $\#(A)-1$. By $(1)$, we obtain ${\rm stdim}(A)=\#(A)-1$.

(3) An Artin algebra has only finitely many nonisomorphic, indecomposable, projective modules. This implies:

(*) If $f$ is an idempotent element of $A$ and $I$ is an idempotent ideal of $A$ such that $AfA\subseteq I$, then there is an idempotent element $f'$ of $A$ which is orthogonal to $f$ such that $I=A(f+f')A$.

Now let $n:={\rm stdim}(A)\geq 1$. On the one hand, since $e_{\leq n-1}$ in Definition 4.7(b) is a strong idempotent element of $A$, we have ${\rm stdim}(A)={\rm stdim}(e_{\leq n-1}Ae_{\leq n-1})+1$ and ${\rm stdim}(A/Ae_{\leq n-1}A)=0$ by (*) and Corollary 4.4(2). On the other hand, for each nontrivial strong idempotent element $e$ of $A$, it follows again from (*) and Corollary 4.4(2) that ${\rm stdim}(eAe)+{\rm stdim}(A/AeA)+1\leq n$. Thus, $(3)$ holds.

(4) Let $m:={\rm stdim}(B)$ and $\ell :=n+m$. If $\ell =0$ (that is, $n=0=m$), then the inequality obviously holds. Let $\ell \geq 1$. Without loss of generality, suppose $n\geq 1$. By the proof of $(3)$, there is a nonzero strong idempotent element $e$ of $A$ with $AeA\neq A$ such that ${\rm stdim}(eAe)=n-1$ and ${\rm stdim}(A/AeA)=0$. Then the canonical surjection $\pi : A\to A/AeA$ is homological. For two homological ring epimorphisms $\lambda _i: R_i\to S_i$ of algebras over the field $k$ with $i=1,2$, the tensor product $\lambda _1\otimes _k\lambda _2: R_1\otimes _k R_2\to S_1\otimes _k S_2$ is again a homological ring epimorphism. This is due to the isomorphism

\begin{align*} {\rm Tor}_j^{R_1\otimes_k R_2}(S_1\otimes_k S_2, S_1\otimes_k S_2)\simeq\bigoplus_{p+q=j}{\rm Tor}_p^{R_1}(S_1,S_1)\otimes_k{\rm Tor}^{R_2}_q(S_2, S_2) \quad \text{for all } j\in\mathbb{N}. \end{align*}

Now let $C:=A\otimes _kB$ and $e':=e\otimes 1\in C$. Then the surjection $\pi \otimes 1: C\to (A/AeA)\otimes _k B$ is homological. Clearly, there are algebra isomorphisms $(A/AeA)\otimes _k B \simeq C/(AeA\otimes _kB)\simeq C/Ce'C$. It follows that the canonical surjection $C\to C/Ce'C$ is homological, and therefore $e'$ is a nontrivial strong idempotent element of $C$. By $(3)$, ${\rm stdim}(C)\geq {\rm stdim}(eAe\otimes _k B)+{\rm stdim}((A/AeA)\otimes _k B)+1$. Moreover, by induction, ${\rm stdim}(eAe\otimes _k B)\geq ({\rm stdim}(eAe)+1)({\rm stdim}(B)+1)-1$ and ${\rm stdim}((A/AeA)\otimes _k B)\geq {\rm stdim}(B)$. Thus, ${\rm stdim}(C)\geq (n+1) (m+1)-1$.

Definition 4.10 Let $A$ be an Artin algebra over a commutative Artin ring $k$. The rational number ${{\rm stdim}(A)}{\#(A)}$ is called the stratified ratio of $A$ and denoted by ${\rm sr}(A)$.

By Proposition 4.9(1), ${\rm sr}(A)\in \mathbb {Q}\cap [0,1)$. Let $A^n$ denote the product of $n$ copies of $A$. Then

\begin{align*} \lim_{n\to\infty}{\rm sr}(A^n)=\lim_{n\to\infty}\frac{n({\rm stdim}(A))+n-1}{n\;\#(A)}=\frac{{\rm stdim}(A)+1}{\#(A)}\leq 1. \end{align*}

In particular, if ${\rm stdim}(A)=\#(A)-1$ (for example, $A$ is quasi-hereditary or local), then $\lim _{n\to \infty }{\rm sr}(A^n)=1$. In § 5, for a gendo-symmetric algebra with infinite dominant dimension, we construct a series of indecomposable symmetric algebras $S_n$ such that $\lim _{n\to \infty }{\rm sr}(S_n)=1$ (see Corollary 5.12 for details).

4.3 Construction of recollements from mirror-reflective algebras

In this subsection we construct explicitly derived recollements from mirror-reflective algebras.

Throughout this subsection we retain all notation in Section 3.1. Recall that $R:=R(A,e)$, $S:=S(A,e)$ and $\bar {e}:=e\otimes e\in R$.

Proposition 4.11 Let $A_2:={\rm End}_R(R\oplus R/I)$ and $B_2:={\rm End}_{S}(S\oplus S/I)$. Suppose that the right $A$-module $eA_A$ is faithful. Then the following statements hold true.

1. (1) There are standard recollements of derived module categories

   
   induced by idempotent ideals that are finitely generated and projective as right modules over $A_2$ and $B_2$, respectively.

2. (2) ${\rm stdim}(A_2)\geq 2{\rm stdim}(A)+1$ and ${\rm stdim}(B_2)\geq {\rm stdim}(A)+{\rm stdim}((1-e)A(1-e))+1$.

3. (3) ${\rm gldim}(A^{\rm op})\leq {\rm gldim}(A_2^{\rm op})\leq 2{\rm gldim}(A^{\rm op})+2$, ${\rm findim}(A^{\rm op})\leq {\rm findim}(A_2^{\rm op})\leq 2{\rm findim}(A^{\rm op})+2$.

Proof. (1) Let $e_2$ be the idempotent of $A_2$ corresponding to the direct summand $R/I$ of the $R$-module $R\oplus R/I$. Then $e_2A_2e_2\simeq R/I$ and $A_2/A_2e_2A_2\simeq R/{\rm Ann}_{R^{\rm op}}(I)$ as algebras. By Lemma 4.5(1), the $A_2^{\rm op}$-module $A_2e_2A_2$ is finitely generated and projective. This implies that $e_2$ is a strong idempotent of $A_2$.

Let $f_2$ be the idempotent of $B_2$ corresponding to the direct summand $S/I$ of the $S$-module $S\oplus S/I$. Similarly, by Lemma 4.5(1), $f_2B_2f_2\simeq S/I$ and $B_2/B_2f_2B_2\simeq S/{\rm Ann}_{S^{\rm op}}(I)$ as algebras, the $B_2^{\rm op}$-module $B_2f_2B_2$ is finitely generated and projective, and thus $f_2$ is a strong idempotent of $B_2$.

Since $eA_A$ is faithful, $J={\rm Ann}_{R^{\rm op}}(I)$ by Lemma 3.5(1). Note that $I$ is an ideal of $S$ and ${\rm Ann}_{S^{\rm op}}(I)=S\cap {\rm Ann}_{R^{\rm op}}(I)=S\cap J$. By Lemma 3.4(4), there are algebra isomorphisms $A\simeq R/I\simeq R/J\simeq S/(S\cap J)$ and $S/I\simeq (1-e)A(1-e)$, and therefore

\begin{align*} e_2A_2e_2\simeq A\simeq A_2/A_2e_2A_2,\quad f_2B_2f_2\simeq (1-e)A(1-e)\quad \text{and}\quad B_2/B_2f_2B_2\simeq A. \end{align*}

Since $e_2$ is a strong idempotent of $A_2$ and $f_2$ is a strong idempotent of $B_2$, $(1)$ holds.

(2) By the proof of (1), $e_2$ and $f_2$ are strong idempotents in $A_2$ and $B_2$, respectively. Thus, ${\rm stdim}(A_2)\ge 1$ and ${\rm stdim}(B_2)\ge 1$. Then (2) follows from Proposition 4.9(3).

(3) This will be shown by some general formulas on the global and finitistic dimensions of rings.

Let $\Gamma$ be a ring and $f$ a strong idempotent element of $\Gamma$. By Definition 4.2, we have

\begin{align*} \mathrm{(a)} \quad{\rm gldim}(\Gamma/\Gamma f \Gamma)\leq {\rm gldim}(\Gamma). \end{align*}

Applying [CX17, Theorem 3.17(2)] to the standard recollement

where $i_*$ is the derived restriction functor induced from the canonical surjection $\Gamma \to \Gamma /\Gamma f \Gamma$ and $j_!$ is the left-derived functor $\Gamma f\otimes ^{\mathbb {L}}_{f\Gamma f}-$, we obtain

\begin{align*} \mathrm{(b)} \quad {\rm gldim}(\Gamma)\leq {\rm gldim}(f\Gamma f)+{\rm gldim}(\Gamma/\Gamma f \Gamma)+{\rm pdim}({_\Gamma}\Gamma/\Gamma f \Gamma)+1. \end{align*}

Moreover, by [CX17, Corollary 3.12], if ${_\Gamma }\Gamma /\Gamma f \Gamma$ has a finite projective resolution by finitely generated projective $\Gamma$-modules, then

\begin{align*} \mathrm{(c)} \quad {\rm findim}(\Gamma/\Gamma f \Gamma)\leq {\rm findim}(\Gamma)\leq {\rm findim}(f\Gamma f)+{\rm findim}(\Gamma/\Gamma f \Gamma)+{\rm pdim}({_\Gamma}\Gamma/\Gamma f \Gamma)+1. \end{align*}

Let $\Gamma :=A_2^{\rm op}$ and $f:=e_2^{\rm op}$. Then $f\Gamma f\simeq A^{\rm op}\simeq \Gamma /\Gamma f\Gamma$ as rings. By the proof of $(1)$ (see the first paragraph), the $\Gamma$-module $\Gamma f\Gamma$ is finitely generated and projective, and the element $f$ is a strong idempotent of $\Gamma$. Thus, (a) and (b) imply $(3)$ on global dimensions, while $({\rm c})$ gives $(3)$ on finitistic dimensions.

We now consider $n$-idempotent and stratifying ideals of mirror-reflective algebras.

Proposition 4.12

1. (1) The ideals $I$ and $J$ of $R$ are $2$-idempotent.

2. (2) Let $n\ge 1$ be an integer. Then $I$ is $(n+2)$-idempotent if and only if so is $J$ if and only if ${\rm Tor}_i^{eAe}(Ae, eA)=0$ for all $1\leq i\leq n$.

3. (3) If ${\rm Tor}_i^{eAe}(Ae, eA)=0$ for all $i\geq 1$, then there are standard recollements of derived module categories induced by $I:=R\bar {e}R$:

   

Proof. (1) There is a commutative diagram

where $\mu$ and $\mu '$ are the multiplication maps. By Lemma 3.5(2), $\pi _2\otimes \pi _2$ is an isomorphism. Note that the composition of the inverse of $\pi _2\otimes \pi _2$ with $\mu$ is the identity of $Ae\otimes _{eAe}eA$. Thus, $\mu$ is an isomorphism. This shows that $I$ is $2$-idempotent by Lemma 4.3(1). Similarly, we can show that $J$ is $2$-idempotent by using the idempotent element $e-\overline {e}$ and the algebra homomorphism $\pi _1$.

(2) By Lemma 3.4(3), $I$ is $(n+2)$-idempotent if and only if so is $J$. Since $I$ is $2$-idempotent by $(1)$, it follows from Lemma 4.3(1) that $I$ is $(n+2)$-idempotent if and only if ${\rm Tor}_i^{\overline {e}R\overline {e}}(R\overline {e}, \overline {e}R)=0$ for $1\leq i\leq n$. By Lemma 3.5(2), $\pi _2$ induces isomorphisms of abelian groups ${\rm Tor}_i^{\overline {e}R\overline {e}}(R\overline {e}, \overline {e}R)\simeq {\rm Tor}_i^{eAe}(Ae, eA)$ for all $i\in \mathbb {N}$. Thus, $I$ is $(n+2)$-idempotent if and only if ${\rm Tor}_i^{eAe}(Ae, eA)=0$ for $1\leq i\leq n$.

(3) By $(2)$, $I$ is a stratifying ideal in $R$ if and only if ${\rm Tor}_i^{eAe}(Ae, eA)=0$ for all $i\geq 1$. According to Corollary 4.4(1), if $I$ is a stratifying ideal in $R$, then $e_0Ie_0$ is a stratifying ideal in $S$. By Lemmas 3.4 and 3.5(2), $e_0Ie_0=I$, $S/I\simeq (1-e)A(1-e)$, $R/I\simeq A$ and $\overline {e}R\overline {e}\simeq eAe\simeq \overline {e}S\overline {e}$. Thus, the recollements in $(3)$ exist.

5. Iterated mirror-reflective algebras and Tachikawa's second conjecture

This section is devoted to proofs of all results stated in the introduction. We first show that mirror-reflective algebras of gendo-symmetric algebras at any levels are symmetric (see Proposition 5.2). Based on this result, we construct not only gendo-symmetric algebras of strictly increasing dominant dimensions and higher minimal Auslander–Gorenstein algebras (see Theorem 1.4), but also recollements of derived module categories of these algebras (see Theorem 1.2). The recollements constructed are then applied to give a new formulation of Tachikawa's second conjecture for symmetric algebras in terms of stratified dimensions and ratios (see Theorem 5.13). Consequently, a sufficient condition is given for the conjecture to hold for symmetric algebras (see Theorem 1.1(II)).

Throughout this section all algebras considered are finite-dimensional algebras over a field $k$.

5.1 Relations among mirror-reflective, symmetric and gendo-symmetric algebras

Let $A$ be an algebra, $e^2=e\in A$ and $\Lambda :=eAe$. Suppose that there is an isomorphism $\iota : eA\to D(Ae)$ of $\Lambda$-$A$-bimodules. Let $\iota _e:=(e)\iota \in D(Ae)={\rm Hom}_k(Ae,k)$. Then $\iota _e=e\iota _e=\iota _ee$. Moreover, $\iota$ is nothing other than the left multiplication map by $\iota _e$. Define $\zeta :Ae\otimes _\Lambda eA\to k$ to be the composition of the maps

\begin{align*} Ae\otimes_\Lambda eA\stackrel{\;{\rm id}\otimes\iota\;}{\longrightarrow} Ae\otimes_\Lambda D(Ae)\stackrel{{\rm ev}}{\longrightarrow}k \end{align*}

where ${\rm ev}$ stands for the evaluation map: $ae\otimes f\mapsto (ae)f$ for $a\in A$ and $f\in D(Ae)$. Then $\zeta$ is given by $(ae\otimes eb)\zeta =(bae)\iota _e=(ebae)\iota _e$ for $a, b\in A$. To any element $\lambda \in Z(\Lambda )$, two maps of $k$-spaces are associated:

\begin{gather*} \chi:\;\; R(A,e,\lambda)=A\oplus Ae\otimes_\Lambda eA \longrightarrow k,\\ a+\sum_{i=1}^n a_ie\otimes eb_i \mapsto \sum_{i=1}^n(a_ie\otimes eb_i)\zeta=\sum_{i=1}^n(eb_ia_ie)\iota_e \quad \text{for } a_i, b_i\in A,\\ \gamma:\;\; Ae\otimes_\Lambda eA\longrightarrow D(A),\\ ae\otimes eb\mapsto [a'\mapsto (eba'ae)\iota_e \ \text{for}\ a,a', b\in A]. \end{gather*}

Lemma 5.1

1. (1) For any $r_1, r_2\in R(A,e,\lambda )$, $(r_1\ast r_2)\chi =(r_2\ast r_1)\chi$, where $\ast$ denotes the multiplication of $R(A,e,\lambda )$.

2. (2) The map $\gamma$ is a homomorphism of $A$-$A$-bimodules. It is an isomorphism if and only if the map $(\cdot e): {\rm End}_{A^{\rm op}}(A)\to {\rm End}_{\Lambda ^{\rm op}}(Ae)$ induced from right multiplication by $e$ is an isomorphism of algebras.

3. (3) If $\epsilon :D(A)\to k$ denotes the map sending $f\in D(A)$ to $(1)f$, then $\zeta =\gamma \,\epsilon$.

Proof. (1) It suffices to show $((a_1+ae\otimes eb)\ast (a_2+a'e\otimes eb'))\chi =((a_2+a'e\otimes eb')\ast (a_1+ae\otimes eb))\chi$ for any $a, a', b,b', a_1,a_2\in A$. Indeed, this follows from $(a'(ae\otimes eb))\zeta =((ae\otimes eb)a')\zeta$ and $((ae\otimes eb)\otimes (a'e\otimes eb'))\omega _\lambda \zeta =((a'e\otimes eb')\otimes (ae\otimes eb))\omega _\lambda \zeta$, by the definitions of $\zeta$ and $\omega _\lambda$ in Section 3.1.

(2) There is a canonical isomorphism $\varphi :\;\; Ae\otimes _\Lambda D(Ae)\rightarrow D({\rm End}_{\Lambda ^{\rm op}}(Ae))$, $ae\otimes f\mapsto [g\mapsto (ae)gf]$ for $a\in A$, $f\in D(Ae)$ and $g\in {\rm End}_{\Lambda ^{\rm op}}(Ae)$. Let $\vartheta : A\to {\rm End}_{A^{\rm op}}(A)$ be the isomorphism which sends $a$ to $(a\cdot )$. Then the composition of the maps

\begin{align*} Ae\otimes_\Lambda eA\stackrel{\;Ae\otimes\iota\;}{\longrightarrow} Ae\otimes_\Lambda D(Ae)\stackrel{\varphi}{\longrightarrow}D({\rm End}_{\Lambda^{\rm op}}(Ae))\stackrel{D(\cdot e)}{\longrightarrow} D({\rm End}_{A^{\rm op}}(A))\stackrel{D(\vartheta)}{\longrightarrow}D(A) \end{align*}

coincides with $\gamma$. Clearly, all the maps above are homomorphisms of $A$-$A$-bimodules. Thus, $\gamma$ is a homomorphism of $A$-$A$-bimodules. Since $D:k\text {-mod}\to k\text {-mod}$ is a duality, $\gamma$ is an isomorphism if and only if the map $(\cdot e)$ in $(2)$ is an isomorphism of algebras.

(3) This follows from $(ae\otimes eb)\zeta =(ebae)\iota _e$ for $a,b\in A$.

From now on, let $(A, e)$ be a gendo-symmetric algebra. Then ${\rm add}(Ae)$ coincides with the full subcategory of $A\text {-mod}$ consisting of projective-injective $A$-modules. If $e'$ is another idempotent element of $A$ such that ${\rm add}(Ae)={\rm add}(Ae')$, then the mirror-reflective algebras $R(A,e)$ and $R(A,e')$ are isomorphic as algebras by Lemma 3.6(1). So, for simplicity, we write $R(A)$ for $R(A,e)$.

In the following, we describe $R(A)$ as a deformation of the trivial extension of $A$. Let $\Lambda :=eAe$ and $\iota : eA\to D(Ae)$ be an isomorphism of $\Lambda$-$A$-bimodules (see Lemma 2.2(2)). Then $\Lambda$ is symmetric and $eA$ is a generator over $\Lambda$. Moreover, there are algebra isomorphisms $A\simeq {\rm End}_\Lambda (eA)$ and $A^{\rm op}\simeq {\rm End}_{\Lambda ^{\rm op}}(Ae)$. By Lemma 5.1(2), there is an isomorphism of $A$-$A$-bimodules: $\gamma :\;\;Ae\otimes _\Lambda eA\stackrel {\simeq }{\longrightarrow } D(A)$. Since $A\simeq {\rm End}_\Lambda (eA)$ and $eA$ is a generator over $\Lambda$, the functor $e(-)e: A^{e}\text {-Mod}\to \Lambda ^e\text {-Mod}$ between the categories of bimodules induces an algebra isomorphism $Z(A)\to Z(\Lambda )$. So, for $\lambda \in Z(\Lambda )$, there exists a unique element $\lambda '\in Z(A)$ such that $e\lambda 'e=\lambda$. Define $\overline {\omega _e}:=(\gamma \otimes \gamma )^{-1}\omega _e\gamma :\;\; D(A)\otimes _AD(A)\stackrel {\simeq }{\longrightarrow } D(A)$ and $F =Ae\otimes _\Lambda -\otimes _\Lambda eA: \Lambda ^{e}\text {-Mod}\to A^{e}\text {-Mod}$. We obtain the following commutative diagram.

Define $\overline {\omega _\lambda }:=\overline {\omega _e}(\cdot \lambda '): \;\; D(A)\otimes _AD(A)\longrightarrow D(A)$. We now extend $\overline {\omega _\lambda }$ to a multiplication on the direct sum $A\oplus D(A)$ by setting

\begin{align*} (A\oplus D(A))\times (A\oplus D(A))\longrightarrow A\oplus D(A),\quad ((a, f), (b,g))\mapsto (ab, ag+fb+(f\otimes g)\overline{\omega_\lambda}) \end{align*}

for $a,b\in A$ and $f,g\in D(A)$. Denote by $A\ltimes _\lambda D(A)$ the abelian group $A\oplus D(A)$ with the above-defined multiplication. By Lemma 3.3(1), $A\ltimes _\lambda D(A)$ is an algebra with an algebra isomorphism

\begin{align*} \overline{\gamma}:=\bigg(\begin{array}{@{}cc@{}} \text{Id}_A & 0 \\ 0 & \gamma \end{array}\bigg):\;\; R(A,e,\lambda)\stackrel{\simeq}{\longrightarrow} A\ltimes_\lambda D(A). \end{align*}

Compared with the trivial extension $A\ltimes D(A)$, the following result, suggested by Kunio Yamagata, shows that $A\ltimes _\lambda D(A)$ is also a symmetric algebra for any $\lambda$.

Proposition 5.2 If $(A, e)$ is a gendo-symmetric algebra, then $R(A,e,\lambda )$ is symmetric for $\lambda \in Z(\Lambda )$.

Proof. Let $R:=R(A,e,\lambda )$. Applying $\chi :R\to k$, we define a bilinear form $\widetilde {\chi }: R\times R\to k$, $(r_1,r_2)\mapsto (r_1\ast r_2)\chi$ for $r_1, r_2\in R$. By Lemma 5.1(1), $\widetilde {\chi }$ is symmetric. To show that $R$ is a symmetric algebra, it suffices to show that $\widetilde {\chi }$ is nondegenerate.

Let $T:=A\ltimes _\lambda D(A)$ and $\psi :=\overline {\gamma }^{-1}\chi :T\to k$. Since $\overline {\gamma }:R\to T$ is an algebra isomorphism, $\psi$ induces a symmetric bilinear form $\widetilde {\psi }:T\times T\to k$, $(t_1, t_1)\in T\times T\mapsto (t_1t_2)\psi$. Clearly, $\widetilde {\chi }$ is nondegenerate if and only if so is $\widetilde {\psi }$. Further, by Lemma 5.1(3), $\psi$ is given by $(a, f)\mapsto (1)f$ for $a\in A$ and $f\in D(A)$. This implies that $((a, f), (b,g))\widetilde {\psi }=(a)g+(b)f+(1)(f\otimes g)\overline {\omega _\lambda }$ for $b\in A$ and $g\in D(A)$. We now show that $\widetilde {\psi }$ is nondegenerate.

Let $(a,f)\neq 0$. Then $a\neq 0$ or $f\neq 0$. If $f\neq 0$, then there is an element $b\in A$ such that $(b)f\neq 0$, and therefore $((a, f), (b,0))\widetilde {\psi }=(b)f\neq 0$. If $f=0$ and $a\neq 0$, then the canonical isomorphism $A\simeq DD(A)$ implies that there is an element $g\in D(A)$ such that $(a)g\neq 0$. In this case, $((a, 0), (0,g))\widetilde {\psi }=(a)g\neq 0$. Thus, $\widetilde {\psi }$ is nondegenerate.

Compared with $R(A)$, the algebra $S(A,e)$ depends on the choice of $e$, that is, if $f=f^2\in A$ such that $(A,f)$ is gendo-symmetric, then $S(A,e)$ and $S(A,f)$ do not have to be isomorphic in general. The following result collects basic homological properties of $S(A,e)$.

Proposition 5.3 Let $S:=S(A,e)$ and $B_0:=(1-e)A(1-e)$. Then:

1. (1) $S$ is a symmetric algebra.

2. (2) $B_0$ can be regarded as an $S$-module via the surjective homomorphism $S\to S/S\overline {e}S\simeq B_0$ and contains no nonzero projective $S$-modules as direct summands.

3. (3) If ${\rm add}({_A}Ae)\cap {\rm add}({_A}A(1-e))=0$, then $\#(S)=\#(A)$. Moreover, if $B_0$ is indecomposable as an algebra, then so is $S$.

Proof. (1) Let $R:=R(A)$, $\bar {e}:=e\otimes e\in R$ and $e_0:=(1-e)+\overline {e}\in R$. Since $R$ is symmetric by Proposition 5.2(1) and $S=e_0Re_0$ by Lemma 3.4(1), $S$ is symmetric.

(2) Since $\pi _1$ induces a surjective algebra homomorphism $\pi _1': S\to B_0$ such that $S/S\overline {e}S\simeq B_0$ (see Lemma 3.4 for notation), $B_0$ can be regarded as an $S$-module. Assume that the $S$-module $B_0$ contains an indecomposable projective direct summand $X$. Then there is a primitive idempotent element $f\in A$ such that $1-e=f+f'$ with $f$ and $f'$ orthogonal idempotent elements in $A$, and $X\simeq Sf$ as $S$-modules. Clearly, $S\overline {e}Sf=0$, $(f)\pi _2'=f$, $(1-e)\pi _2'=1-e$ and $(S\overline {e}Sf)\pi _2'=AeAf$. Consequently, ${\rm Hom}_A(Ae,Af)\simeq eAf=0$, and therefore ${\rm Hom}_A(Af, Ae)\simeq D\,{\rm Hom}_A(Ae,Af)=0$. By Lemma 2.2(2), $Af$ can be embedded into $(Ae)^n$ for some $n\geq 1$. This implies $Af=0$, a contradiction.

(3) Since $\bar {e}S\bar {e}\simeq eAe$ by Lemma 3.5(2), it follows from $(2)$ that $\#S(A)=\#(eAe)+\#(B_0)$. Due to ${\rm add}(Ae)\cap {\rm add}(A(1-e))=0$, we have $\#(A)=\#(eAe)+\#(B_0)$ and $\#S(A)=\#(A)$. The second assertion in $(3)$ follows from Proposition 3.7(2).

5.2 Mirror-reflective algebras and Auslander–Gorenstein algebras

In this subsection we construct new gendo-symmetric algebras from minimal Auslander–Gorenstein algebras. Consequently, there is a series of algebras such that in each step the dominant dimensions increase at least by $2$. This is based on study of mirror-reflective algebras. Finally, we will give a proof of Theorem 1.4, which will be partially used to prove Theorem 1.2(2).

By Lemma 3.4, we have an algebra automorphism $\phi :R(A)\to R(A)$ and two surjective algebra homomorphisms $\pi _1, \pi _2: R(A)\to A$ such that $\pi _2=\phi \pi _1$. Through $\pi _1$ we regard $A$-modules as $R(A)$-modules in the following discussion. Thus, $A\text {-mod}$ is a Serre subcategory of $R(A)\text {-mod}$, that is, it is closed under direct summands, submodules, quotients and extensions in $R(A)\text {-mod}$. Let

\begin{align*} \phi_*: R(A)\text{-mod}\longrightarrow R(A)\text{-mod} \quad \text{and} \quad (\pi_2)_*:A\text{-mod}\longrightarrow R(A)\text{-mod} \end{align*}

be the restriction functors induced by $\phi$ and $\pi _2$, respectively. Then $\phi _*$ is an auto-equivalence and $\phi _*(X)=(\pi _2)_*(X)$ for $X\in A\text {-mod}$.

Lemma 5.4 Suppose that $\Lambda$ is a symmetric algebra and $N$ is a basic $\Lambda$-module without nonzero projective direct summands. Let $A:={\rm End}_\Lambda (\Lambda \oplus N)$, $e$ be an idempotent element of $A$ corresponding to the direct summand $\Lambda$ of $\Lambda \oplus N$, and $R:=R(A, e)$. If ${_\Lambda }N$ is $m$-rigid for a natural number $m$, then the following statements hold.

1. (1) The $R$-module $A(1-e)$ is $(m+2)$-rigid and there are isomorphisms of $R$-modules:

   \begin{align*} \Omega_R^{m+3}(A(1-e))\simeq\Omega_R^{m+2}(\phi_*(Ae\otimes_\Lambda N))\simeq \phi_*({\rm Hom}_\Lambda(eA, \Omega_\Lambda^{m+2}(N))). \end{align*}

2. (2) If $\Omega _\Lambda ^{m+2}(N)\simeq N$, then $\Omega _R^{m+3}(A(1-e))\simeq \phi _*(A(1-e))$ and the $R$-module $A(1-e)$ is $(2m+4)$-rigid. In this case, $\Omega _R^{2m+6}(A(1-e))\simeq A(1-e)$.

Proof. (1) By the proof of Proposition 4.12(2), $\pi _2$ induces an isomorphism ${\rm Tor}_i^{\overline {e}R\overline {e}}(R\overline {e}, \overline {e}R)\simeq {\rm Tor}_i^\Lambda (Ae, eA)$ for all $i\geq 1$. Since $\Lambda$ is symmetric and $D(Ae)\simeq eA$ by Lemma 2.2(2), we have

\begin{align*} D{\rm Tor}_i^\Lambda(Ae, eA)\simeq{\rm Ext}_\Lambda^i(eA, D(Ae))\simeq{\rm Ext}_\Lambda^i(eA, eA)={\rm Ext}_\Lambda^i(\Lambda\oplus N, \Lambda\oplus N)\simeq{\rm Ext}_\Lambda^i(N,N). \end{align*}

As ${_\Lambda }N$ is $m$-rigid, we have ${\rm Tor}_i^{\overline {e}R\overline {e}}(R\overline {e}, \overline {e}R)=0$ for $1\leq i\leq m$. By Proposition 4.12(1), $I:=R\overline {e}R$ is $2$-idempotent. Therefore, $I$ is $(m+2)$-idempotent by Lemma 4.3(1). Further, it follows from Lemma 4.3(2) that ${_R}R/I$ is $(m+2)$-rigid. Since $R/I\simeq A$ as $R$-modules, $_RA$ is $(m+2)$-rigid. Note that ${_R}A\simeq R(e-\overline {e})\oplus A(1-e)$ by Lemma 3.5(2). As $R$ is symmetric by Proposition 5.2, we see that $R(e-\overline {e})$ is projective-injective. Consequently, ${_R}A(1-e)$ is $(m+2)$-rigid.

The proof of Proposition 4.12(1) implies $I\simeq R\overline {e}\otimes _{\overline {e}R\overline {e}}\overline {e}R$ as $R$-$R$-bimodules. By Lemma 3.5(2), $\pi _2$ restricts to an algebra isomorphism $\overline {e}R\overline {e}\to \Lambda$ and also an isomorphism $R\overline {e}\to Ae$ of abelian groups. Via the algebra isomorphism, we can regard $R\overline {e}$ as an $R$-$\Lambda$-bimodule. Then $R\overline {e}\simeq (\pi _2)_*(Ae)=\phi _*(Ae)$ as $R$-$\Lambda$-bimodules. This gives a natural isomorphism $R\overline {e}\otimes _\Lambda -\stackrel {\simeq }{\longrightarrow } \phi _*(Ae)\otimes _\Lambda -$ of functors from $\Lambda \text {-proj}$ to $R\text {-proj}$. Since $N$ has no nonzero projective direct summands, ${\rm add}({_A}Ae)\cap {\rm add}({_A}A(1-e))=0$. From $A\otimes _RR\overline {e}\simeq Ae\simeq R\overline {e}$ and $A\otimes _RR(1-e)\simeq A(1-e)$, we obtain ${\rm add}(R\overline {e})\cap {\rm add}(R(1-e))=0$. Since $I(1-e)$ is isomorphic to $R\overline {e}\otimes _{\overline {e}R\overline {e}}\overline {e}R(1-e)$, which is a quotient module of $(R\overline {e})^n$ for some $n$, we deduce that $I(1-e)$ does not contain nonzero direct summands in ${\rm add}(R(1-e))$. Thus, the surjection ${_R}R(1-e)\to A(1-e)$ induced by $\pi _1$ is a projective cover of the $R$-module $A(1-e)$, and therefore $\Omega _R(A(1-e))=I(1-e)$. Since $\pi _2$ induces an isomorphism $\overline {e}R\to eA$ and sends $1-e$ to $1-e$ by Lemma 3.5(2), we have $\overline {e}R(1-e)\simeq eA(1-e)$ and

\begin{align*} \Omega_R(A(1-e))\simeq R\overline{e}\otimes_{\overline{e}R\overline{e}}eA(1-e)\simeq R\overline{e}\otimes_\Lambda eA(1-e)\simeq \phi_*(Ae)\otimes_\Lambda N=\phi_*(Ae\otimes_\Lambda N). \end{align*}

Let $\cdots \to Q_{m+1}\stackrel {\partial }{\longrightarrow } Q_m\to \cdots \to Q_1\to Q_0\to N\to 0$ be a minimal projective resolution of $_\Lambda N$. Then it follows from $eA(1-e)=N$ and ${\rm Tor}_i^\Lambda (Ae, N)\simeq D\,{\rm Ext}_\Lambda ^i(N,N)=0$ for $1\leq i\leq m$ that the sequence

\begin{align*} Ae\otimes_\Lambda Q_{m+1}\stackrel{Ae\otimes\partial}{\longrightarrow} Ae\otimes_\Lambda Q_m\longrightarrow\cdots\longrightarrow Ae\otimes_\Lambda Q_1\longrightarrow Ae\otimes_\Lambda Q_0\longrightarrow Ae\otimes_\Lambda N\longrightarrow 0 \end{align*}

is exact. As the composition of ${_A}Ae\otimes _\Lambda -$ with $(e\cdot )$ is isomorphic to the identity functor of $\Lambda \text {-mod}$, we have $\Omega _A^{m+2}(Ae\otimes _\Lambda N)\simeq {\rm Ker}(Ae\otimes \partial )$. Note that $Ae\otimes _\Lambda -\simeq {\rm Hom}_\Lambda (eA,-): \Lambda \text {-proj}\stackrel {\simeq }{\longrightarrow }{\rm add}({_A}Ae)$ since $Ae={\rm Hom}_\Lambda (\Lambda \oplus N, \Lambda )$. This shows ${\rm Ker}(Ae\otimes \partial )\simeq {\rm Hom}_\Lambda (eA,{\rm Ker}(\partial ))={\rm Hom}_\Lambda (eA,\Omega _\Lambda ^{m+2}(N))$, and therefore

\begin{align*} \Omega_R^{m+3}(A(1-e))\simeq\Omega_R^{m+2}(\phi_*(Ae\otimes_\Lambda N))\simeq \phi_*(\Omega_R^{m+2}(Ae\otimes_\Lambda N))\simeq\phi_*({\rm Hom}_\Lambda(eA,\Omega_\Lambda^{m+2}(N))). \end{align*}

(2) Let $X:=A(1-e)$. Suppose $\Omega _\Lambda ^{m+2}(N)\simeq N$. Then $\Omega _R^{m+3}(X)\simeq \phi _*({\rm Hom}_\Lambda (eA,eX))$. Since the functor $(e\cdot ): A\text {-mod}\to \Lambda \text {-mod}$ induces an algebra isomorphism ${\rm End}_A(A)\simeq {\rm End}_\Lambda (eA)$, we have $X\simeq {\rm Hom}_A(A,X)\simeq {\rm Hom}_\Lambda (eA,eX)$. It follows that $\Omega _R^{m+3}(X)\simeq \phi _*(X)$. Since $\phi$ is an algebra isomorphism with $\phi ^2={\rm Id}_R$ by Lemma 3.4(3) and since $\Omega _R$ commutes with $\phi _*$, we obtain $\Omega _R^{2m+6}(X)\simeq X$. It remains to show that ${_R}X$ is $(2m+4)$-rigid.

Since $R$ is symmetric, the stable module category $R-{\underline {\textrm mod}}$ of $R$ is a triangulated category with the shift functor $[1]=\Omega ^{-}_R: R-{\underline {\textrm mod}}\to R-{\underline {\textrm mod}}$, where $\Omega ^{-}_R$ is the cosyzygy functor on $R-{\underline {\textrm mod}}$. Clearly, ${\rm Ext}_R^n(X_1, X_2)\simeq \underline {{\rm Hom}}_R(X_1, X_2[n])$ for all $n\geq 1$ and $X_1,X_2\in R\text {-mod}$, where $\underline {{\rm Hom}}_R(X,Y)$ denotes the morphism set from $X$ to $Y$ in ${R-{\underline {\textrm mod}}}$. Since the Auslander–Reiten translation on $R\text {-mod}$ coincides with $\Omega ^2_R$, it follows from the Auslander–Reiten formula that there is a natural isomorphism $D\,\underline {{\rm Hom}}_R(X_1, X_2)\simeq \underline {{\rm Hom}}_R(X_2, X_1[-1])$. Consequently, for $i\in \mathbb {N}$, there are isomorphisms

\begin{align*} {\rm Ext}_R^{m+3+i}(X,X)&\simeq\underline{{\rm Hom}}_R(\Omega_R^{m+3}(X), X[i])\simeq\underline{{\rm Hom}}_R(\phi_*(X), X[i])\\ &\simeq D\,\underline{{\rm Hom}}_R(X[i],\phi_*(X)[-1]). \end{align*}

By Lemma 3.4(3), $\phi$ is an algebra isomorphism with $\phi ^2={\rm Id}_R$. Thus,

\begin{align*} \underline{{\rm Hom}}_R(X[i],\phi_*(X)[-1])&\simeq \underline{{\rm Hom}}_R(\phi_*(X)[i], X[-1])\simeq \underline{{\rm Hom}}_R(\Omega_R^{m+3}(X), X[-1-i])\\ &\simeq {\rm Ext}_R^{m+2-i}(X,X) \end{align*}

for $0\le i\leq m+1$. This implies ${\rm Ext}_R^{m+3+i}(X,X)\simeq D\,{\rm Ext}_R^{m+2-i}(X,X)$ for $0\leq i\leq m+1$. Since $X$ is $(m+2)$-rigid by $(1)$, it is actually $(2m+4)$-rigid.

Proposition 5.5 Suppose that $\Lambda$ is a symmetric algebra and $N$ is a basic $\Lambda$-module without nonzero projective direct summands. Let $A :={\rm End}_\Lambda (\Lambda \oplus N)$, $e$ be an idempotent element of $A$ corresponding to the direct summand $\Lambda$ of $\Lambda \oplus N$, and $R:=R(A, e)$.

1. (1) If ${_\Lambda }\Lambda \oplus N$ is $m$-rigid, then ${_R}R\oplus A(1-e)$ is $(m+2)$-rigid.

2. (2) If ${_\Lambda }\Lambda \oplus N$ is $m$-ortho-symmetric, then ${_R}R\oplus A(1-e)$ is $(2m+4)$-ortho-symmetric.

3. (3) If ${_\Lambda }\Lambda \oplus N$ is maximal $m$-orthogonal, then ${_R}R\oplus A(1-e)$ is maximal $(2m+4)$-orthogonal.

Proof. (1) Since $R$ is a symmetric algebra by Proposition 5.2, (1) follows from Lemma 5.4(1).

(2) By assumption, ${_\Lambda }N$ is basic and contains no nonzero projective direct summands. This implies that ${_A}A(1-e)$ is basic and contains no nonzero projective-injective direct summands. We claim that ${_R}A(1-e)$ contains no nonzero projective direct summands. In fact, by the proof of Lemma 5.4(1), ${_R}R(1-e)$ is a projective cover of ${_R}A(1-e)$. If ${_R}A(1-e)$ contains an indecomposable projective direct summand $Y$, then $Y$ is a direct summand of $R(1-e)$. Since $R$ is symmetric, ${_R}Y$ must be projective-injective. However, since $A\text {-mod}\subseteq R\text {-mod}$ is a Serre subcategory, ${_A}Y$ is also a nonzero projective-injective direct summand of ${_A}A(1-e)$. This is a contradiction and shows that the above claim holds. Then $(2)$ follows from Lemmas 5.4 and 2.3.

(3) Maximal orthogonal modules over an algebra $B$ are exactly ortho-symmetric $B$-modules such that their endomorphism algebras have finite global dimension. Let $A_1:={\rm End}_R(R\oplus A(1-e))$. By $(2)$, to show $(3)$, it suffices to show that ${\rm gldim}(A_1)<\infty$ if ${\rm gldim}(A)<\infty$

Let $B_1:={\rm End}_R(R\oplus A)$. Since ${_R}A\simeq R(e-\overline {e})\oplus A(1-e)$ by the proof of Lemma 5.4(1), we know that $A_1$ and $B_1$ are Morita equivalent, and therefore ${\rm gldim}(A_1)={\rm gldim}(B_1)$. Since the right $A$-module $eA_A$ is faithful, it follows from Proposition 4.11(3) that if ${\rm gldim}(A)<\infty$ then ${\rm gldim}(B_1)={\rm gldim}(B_1^{\rm op})<\infty$. Hence, ${\rm gldim}(A_1)<\infty$.

Proof Proof of Theorem 1.4

The statement (1) follows from Proposition 5.2. Let $R:=R(A)$ and $S:=S(A,e)$. Then $R$ and $S$ are symmetric by $(1)$ and Proposition 5.3(1). Let $A_2:=\mathcal {A}(A,e)$ and $B_2:=\mathcal {B}(A,e)$. Then $A_2$ and $B_2$ are gendo-symmetric.

Next, we show that $(2)$ and $(3)$ hold for $A_2$. In fact, since $A$ is gendo-symmetric, we can identify $A$ with ${\rm End}_\Lambda (\Lambda \oplus X)$, where $\Lambda :=eAe$ is symmetric and $X=eA(1-e)$. As global, dominant and injective dimensions are invariant under Morita equivalences, the classes of minimal Auslander–Gorenstein algebras and of higher Auslander algebras are closed under Morita equivalences. Moreover, for a self-injective algebra $\Gamma$ and $M\in \Gamma \text {-mod}$, it follows from [Mul68, Lemma 3] that ${\rm domdim}({\rm End}_\Gamma (\Gamma \oplus M))$ equals the maximal natural number $n\geq 2$ or $\infty$ such that $M$ is $(n-2)$-rigid. So, for a basic module $X$ that has no nonzero projective direct summands, the inequality ${\rm domdim}(A_2)\geq {\rm domdim}(A)+2$ and the statement $(3)$ follow immediately from Proposition 5.5. Further, for an arbitrary module $X$, the consideration can be reduced by a series of Morita equivalences, as shown below.

We take a direct summand $N$ of $X$ such that $N$ is basic, has no nonzero projective direct summands and satisfies ${\rm add}(\Lambda \oplus N)={\rm add}(\Lambda \oplus X)$. Let $B:={\rm End}_\Lambda (\Lambda \oplus N)$ and $f^2=f\in A$ correspond to the direct summand $\Lambda \oplus N$ of $\Lambda \oplus X$. Then ${_A}Af$ is a progenerator (that is, a projective generator), and therefore $B=fAf$ is Morita equivalent to $A$. Since $ef=e=fe$, we have $R(B)=fAf\oplus fAe\otimes _\Lambda eAf=fRf$. Due to $R\otimes _AAf\simeq Rf$, the module ${_R}Rf$ is a progenerator. Thus, $R$ and $R(B)$ are Morita equivalent. Now let $H:={\rm End}_{R(B)}(R(B)\oplus B(f-e))$. If $A$ is $n$-minimal Auslander–Gorenstein (respectively, $n$-Auslander), then so is $B$, and therefore, so is $H$ by the case proved above. Next, we shall show that $A_2$ and $H$ are Morita equivalent. Actually, the restriction of $\pi _1$ to $A$ is the identity map of $A$. This implies $A\otimes _RRf=Af$ as $R$-modules, and therefore ${\rm add}(_RA)={\rm add}(_RAf)$. Let $A_2':={\rm End}_R(Rf\oplus A(1-e)f)={\rm End}_R(Rf\oplus A(f-e))$. Then $A_2$ and $A_2'$ are Morita equivalent. Since the functor $(f\cdot ): R\text {-mod}\to R(B)\text {-mod}$ is an equivalence and $f(Rf\oplus A(f-e))=R(B)\oplus B(f-e)$, there is an algebra isomorphism $A_2'\simeq H$. Hence, $A_2$ and $H$ are Morita equivalent. Thus, $(2)$ and $(3)$ hold true for $A_2$.

It remains to show ${\rm domdim}(B_2)\geq {\rm domdim}(A)+2$. Up to Morita equivalence, we assume $A={\rm End}_\Lambda (\Lambda \oplus N)$. If ${_\Lambda }\Lambda \oplus N$ is $m$-rigid for some $m\in \mathbb {N}$, then it follows from the first part of the proof of Lemma 5.4(1) that $I$ is an $(m+2)$-idempotent ideal of $R$. Let $e_0:=(1-e)+\overline {e}\in R$. By Lemma 3.4, we have $\overline {e}e_0=\overline {e}=e_0\overline {e}$, $I:=R\overline {e}R=S\overline {e}S$ and $S/I\simeq (1-e)A(1-e)$ as algebras. Thanks to Corollary 4.4(1), $I$ is an $(m+2)$-idempotent ideal of $S$. Further, by Lemma 4.3(2), ${_S}S/I$ is $(m+2)$-rigid, and therefore ${_S}S\oplus S/I$ is $(m+2)$-rigid since $S$ is symmetric by Proposition 5.3(1). Thus, ${\rm domdim}(B_2)\geq {\rm domdim}(A)+2$, due to [Mul68, Lemma 3].

5.3 Recollements of mirror-reflective algebras and Tachikawa's second conjecture

In this subsection we study the iterated process of constructing (reduced) mirror-reflective algebras from gendo-symmetric algebras and prove Theorems 1.1 and 1.2.

Throughout this subsection, let $(A,e)$ be a gendo-symmetric algebra over a field. For $n\ge 1$, we inductively define

\begin{gather*} A_1=B_1:=A,\quad R_1:=R(A_1,e_1), \quad S_1:=S(A_1, f_1),\\ A_{n+1}:={\rm End}_{R_n}(R_n\oplus A_n(1_{A_n}-e_n)),\quad R_{n+1}:=R(A_{n+1}, e_{n+1}),\\ B_{n+1}:={\rm End}_{S_n}(S_n\oplus (1_{B_n}-f_n)B_n(1_{B_n}-f_n)),\quad S_{n+1}:=S(B_{n+1}, f_{n+1}), \end{gather*}

where $e_1=f_1:=e$, and for $n\geq 1$, $e_{n+1}\in A_{n+1}$ is the idempotent element corresponding to the direct summand $R_n$ of the $R_n$-module $R_n\oplus A_n(1_{A_n}-e_n)$, and $f_{n+1}\in B_{n+1}$ is the idempotent element corresponding to the direct summand $S_n$ of the $S_n$-module $S_n\oplus (1_{B_n}-f_n)B_n (1_{B_n}-f_n)$. In other words,

\begin{align*} A_{n+1}=\mathcal{A}(A_n, e_n),\quad B_{n+1}=\mathcal{B}(B_n, f_n)\quad \text{for } n\ge 1 \end{align*}

(see Section 1.3 for notation). For convenience, we set

\begin{align*} R_0=S_0:=eAe \quad\text{and}\quad B_0:=(1-e)A(1-e). \end{align*}

Definition 5.6 For $n\geq 1$, the algebras $R_n$, $S_n$, $A_n$ and $B_n$ are called the $n$th mirror-reflective, reduced mirror-reflective, gendo-symmetric and reduced gendo-symmetric algebras of $(A,e)$, respectively.

By Propositions 5.2 and 5.3(1), the algebras $R_n$ and $S_n$ are symmetric. Thus, $A_n$ and $B_n$ are gendo-symmetric. They are characterized in terms of Morita context algebras in § 4, just before Lemma 4.6. Moreover, it follows from Theorem 1.4(2) that ${\rm domdim}(A_{n+1})\geq {\rm domdim}(A_n)+2$ and ${\rm domdim}(B_{n+1})\geq {\rm domdim}(B_n)+2$. Thus, $\min \{{\rm domdim}(A_n),{\rm domdim}(B_n)\}\geq {\rm domdim}(A)+2(n-1)\geq 2n$.

In the next result we describe the relation between the families $A_n$ and $B_n$ on the one hand and the families $R_n$ and $S_n$ on the other hand by derived and stable equivalences of Morita type. For the definitions and constructions of derived and stable equivalences of Morita type, we refer to the survey article [Xi18].

Lemma 5.7

1. (1) Let $I_n:=R_n\overline {e}_n R_n$ and $J_n:=R_n(e_n-\overline {e}_n)R_n$ with $\overline {e}_n=e_n\otimes e_n\in R_n$ for $n\geq 1$. Then $A_{n+1}$ is derived equivalent and stably equivalent of Morita type to the Morita context algebra $M_l(R_n,I_n,J_n)$.

2. (2) Let $K_n:=S_n\overline {f}_n S_n$ and $L_n:=S_n\cap (R(B_n)(f_n-\overline {f}_n)R(B_n))$ for $n\geq 1$. Then $B_{n+1}$ is derived equivalent and stably equivalent of Morita type to the Morita context algebra $M_l(S_n,K_n, L_n)$.

Proof. (1) There is a surjective algebra homomorphism $\pi _{1,n}: R_n\to A_n$ with ${\rm Ker}(\pi _{1,n})=I_n$ which induces an isomorphism $R_n(e_n-\overline {e}_n)\simeq A_ne_n$ of $R_n$-modules. Thus, $I_n\simeq \Omega _{R_n}(A_n)\oplus Q_n$ with $Q_n$ a projective $R_n$-module, and $A_ne_n$ is a projective $R_n$-module. Hence, $A_{n+1}$ is Morita equivalent to $A_{n+1}':={\rm End}_{R_n}(R_n\oplus A_n)$. Let $C_{n+1}:={\rm End}_{R_n}(R_n\oplus I_n)$. By [HX13, Corollary 1.2], for any self-injective algebra $\Lambda$ and $M\in \Lambda \text {-mod}$, the algebras ${\rm End}_{\Lambda }(\Lambda \oplus M)$ and ${\rm End}_{\Lambda }(\Lambda \oplus \Omega _{\Lambda }(M))$ are almost $\nu$-stable derived equivalent. Since $R_n$ is symmetric, it follows that $A_{n+1}'$ and $C_{n+1}$ are almost $\nu$-stable derived equivalent. By [HX10, Theorem 1.1], each almost $\nu$-stable derived equivalence between finite-dimensional algebras over a field gives rise to a stable equivalence of Morita type. Consequently, $A_{n+1}$ and $C_{n+1}$ are both derived equivalent and stably equivalent of Morita type. It remains to show $C_{n+1}\simeq M_l(R_n,I_n,J_n)$ as algebras.

In fact, since $I_n^2=I_n$, the inclusion $\lambda _n:I_n\hookrightarrow R_n$ induces ${\rm End}_{R_n}(I_n)\simeq {\rm Hom}_{R_n}(I_n, R_n)$. As $R_n$ is symmetric and $J_n={\rm Ann}_{R_n^{\rm op}}(I_n)$ by Lemma 3.5(1), we get $R_n/J_n\simeq {\rm End}_{R_n}(I_n)$ as algebras via the restriction of $\lambda _n$. This yields a series of isomorphisms

\begin{align*} C_{n+1}&\simeq\bigg(\begin{array}{@{}cc@{}} R_n & I_n\\ {\rm Hom}_{R_n}(I_n, R_n) & {\rm End}_{R_n}(I_n) \end{array}\bigg)\simeq \bigg(\begin{array}{@{}cc@{}} R_n & I_n\\ {\rm End}_{R_n}(I_n) & {\rm End}_{R_n}(I_n) \end{array}\bigg)\\ &\simeq \bigg(\begin{array}{@{}cc@{}} R_n & I_n\\ R_n/J_n & R_n/J_n \end{array}\bigg), \end{align*}

of which the composition is an isomorphism from $C_{n+1}$ to $M_l(R_n,I_n,J_n)$ of algebras. This shows $(1)$.

(2) By Lemma 3.4(4), $K_n=R(B_n)\overline {f_n}R(B_n)$ and $S_n/K_n\simeq (1_{B_n}-f_n)B_n(1_{B_n}-f_n)$. By the proof of Proposition 4.11(1), ${\rm Ann}_{S_n^{\rm op}}(K_n)=L_n$. Similarly, since $S_n$ is symmetric, we can show that $B_{n+1}$ and ${\rm End}_{S_n}(S_n\oplus K_n)$ are both derived equivalent and stably equivalent of Morita type, and that ${\rm End}_{S_n}(S_n\oplus K_n)$ is isomorphic to $M_l(S_n,K_n, L_n)$ as algebras.

Remark 5.8 By the proof of Lemma 5.7, $B_{n+1}$ and ${\rm End}_{S_n}(S_n\oplus S_n/K_n)$ are isomorphic, while $A_{n+1}$ and ${\rm End}_{R_n}(R_n\oplus A_n)$ are Morita equivalent. It follows from Proposition 4.11(1) that there are recollements of derived module categories $({\mathscr D}(A_n),{\mathscr D}(A_{n+1}), {\mathscr D}(A_n))$ and $({\mathscr D}(B_n), {\mathscr D}(B_{n+1}), {\mathscr D}(B_0))$, which are induced by finitely generated and right-projective idempotent ideals of $A_{n+1}$ and $B_{n+1}$, respectively.

Proof Proof of Theorem 1.2

We retain all the notation introduced in Lemma 5.7 and its proof.

(1) By Lemma 4.6, there is a recollement $({\mathscr D}(R_n/I_n), {\mathscr D}(M_l(R_n,I_n,J_n)), {\mathscr D}(R_n/J_n))$ induced by a finitely generated, left-projective idempotent ideal of $M_l(R_n,I_n,J_n)$. Thus, the recollement restricts to a recollement of bounded-above derived categories. Since $R_n/I_n\simeq A_n\simeq R_n/J_n$ as algebras and since $A_{n+1}$ and $M_l(R_n,I_n,J_n)$ are derived equivalent by Lemma 5.7(1), there is a recollement $({\mathscr D}^-(A_n), {\mathscr D}^-(A_{n+1}), {\mathscr D}^-(A_n))$.

Similarly, we can apply Lemmas 5.7(2) and 4.6 to show the existence of the recollement $({\mathscr D}^-(S_n/K_n), {\mathscr D}^-(B_{n+1}), {\mathscr D}^-(S_n/L_n))$. Note that there are isomorphisms of algebras $S_n/L_n\simeq B_n$ and

\begin{align*} S_n/K_n & =\simeq (1_{B_n}-f_n)B_n(1_{B_n}-f_n)\simeq (1_{B_{n-1}}-f_{n-1})B_{n-1}(1_{B_{n-1}}-f_{n-1})\simeq\cdots\\ &\simeq(1-f_1)B_1(1-f_1)=B_0. \end{align*}

This implies the existence of the second recollement in $(1)$.

(2) Note that $R_0$ is symmetric, $A\simeq {\rm End}_{R_0}(eA)$ and $D(eA)\simeq Ae$. Suppose ${\rm domdim}(A)=\infty$. By [Mul68, Lemma 3], ${\rm Ext}_{R_0}^i(eA,eA)=0$ for all $i\geq 1$. It follows from ${\rm Ext}_{R_0}^i(eA, eA)\simeq {\rm Ext}_{R_0}^i(eA, D(Ae))\simeq D\,{\rm Tor}_i^{R_0}(Ae, eA)$ that ${\rm Tor}_i^{R_0}(Ae, eA)=0$ for all $i\geq 1$. By Proposition 4.12(3), the recollements in $(2)$ exist for $n=1$. If $n\geq 1$, then $R_n$ and $S_n$ are symmetric algebras, while $A_n$ and $B_n$ are gendo-symmetric algebras. Moreover, ${\rm domdim}(A_n)=\infty ={\rm domdim}(B_n)$ by Theorem 1.4(2) and $(1_{B_n}-f_n)B_n(1_{B_n}-f_n)\simeq B_0$ as algebras. Thus, by induction we can show the existence of recollements for $n\ge 1$.

Theorem 1.2 can be applied to investigate homological dimensions and higher algebraic $K$-groups. As usual, for a ring $R$ and $m\in \mathbb {N}$, we denote by $K_m(R)$ the $m$th algebraic $K$-group of $R$ in the sense of Quillen, and by $nK_m(R)$ the direct sum of $n$ copies of $K_m(R)$ for $n\ge 0$. If $R$ is an Artin algebra, then $K_0(R)$ is a finitely generated free abelian group of rank $\#(R)$.

Lemma 5.9 Let $R$ be a ring with $f^2=f\in R$ such that $I:=RfR$ is a stratifying ideal in $R$. Suppose that one of the following conditions holds.

1. (a) Either ${_R}I$ or $I_R$ is finitely generated and projective.

2. (b) There is a ring homomorphism $\lambda :R/I\to R$ such that the composition of $\lambda$ with the canonical surjection $R\to R/I$ is an isomorphism. Then $K_n(R)\simeq K_n(fRf)\oplus K_n(R/I)$ for $n\in \mathbb {N}$.

Proof. When $(a)$ holds, the isomorphisms of algebraic $K$-groups in Lemma 5.9 follow from [CX16b, Corollary 1.3] or [CX12, Corollary 1.2].

Let $\pi :R\to R/I$ be the canonical surjection. Clearly, $\pi$ is the universal localization of $R$ at the map $0\to Rf$. Since $I$ is a stratifying ideal in $R$, $\pi$ is a homological ring epimorphism (also called stably flat in [NR04]). By [NR04, Theorem 0.5] and [CX16b, Lemma 2.6], the tensor functors $Rf\otimes _{fRf}-: (fRf)\text {-proj}\to R\text {-proj}$ and $(R/I)\otimes _R-:R\text {-proj}\to (R/I)\text {-proj}$ induce a long exact sequence of algebraic $K$-groups of rings

\begin{align*} \cdots\to K_{n+1}(R/I)\to K_n(fRf)\to K_n(R)\to K_n(R/I)\to \cdots\to K_0(fRf)\to K_0(R)\to K_0(R/I). \end{align*}

Suppose (b) holds. Then the composition of the functors $R\otimes _{R/I}-: (R/I)\text {-proj}\to R\text {-proj}$ with $(R/I)\otimes _R-:R\text {-proj}\to (R/I)\text {-proj}$ is an equivalence. This implies that the composition of the maps $K_n(R\otimes _{R/I}-):K_n(R/I)\to K_n(R)$ with $K_n((R/I)\otimes _R-):K_n(R)\to K_n(R/I)$ induced from tensor functors is an isomorphism. Consequently, $0\to K_n(fRf)\to K_n(R)\to K_n(R/I)\to 0$ is split-exact. Thus, $K_n(R)\simeq K_n(fRf)\oplus K_n(R/I)$.

Corollary 5.10 Let $n$ be a positive integer. Then:

1. (1) ${\rm findim}(A_n)\leq {\rm findim}(A_{n+1})\leq 2{\rm findim}(A_n)+2$ and

   \begin{align*} {\rm findim}(B_0)\leq {\rm findim}(B_{n+1})\leq {\rm findim}(B_0)+{\rm findim}(B_n)+2. \end{align*}
   Thus,
   \begin{align*} {\rm findim}(A_{n+1})&\leq 2^n\,{\rm findim}(A) + 2^{n+1} - 2\text{ and } \\{\rm findim}(B_{n+1})&\leq {\rm findim}(A) + n({\rm findim}(B_0)+2). \end{align*}
   Analogous inequalities hold true when finitistic dimension is replaced by global dimension.

2. (2) $K_*(A_{n+1})\simeq 2^n\,K_*(A)$ and $K_*(B_{n+1})\simeq nK_*(B_0)\oplus K_*(A)$ for $*\in \mathbb {N}$.

3. (3) If ${\rm domdim}(A)=\infty$, then $K_*(R_n)\simeq K_*(\Lambda )\oplus (2^n-1)K_*(A)$ and $K_*(S_n)\simeq K_*(\Lambda )\oplus nK_*(B_0)$ for any $*\in \mathbb {N}$.

Proof. (1) By Lemma 5.7(1), $A_{n+1}$ and $M_l(R_n,I_n,J_n)$ are stably equivalent of Morita type. Since global and finitistic dimensions are invariant under stably equivalences of Morita type, $A_{n+1}$ and $M_l(R_n,I_n,J_n)$ have the same global and finitistic dimensions. Then the statements on $A_{n+1}$ in $(1)$ hold by (c) in the proof of Proposition 4.11(3) (or by applying [CX17, Corollary 3.12 and Theorem 3.17] to the recollement $({\mathscr D}(R_n/I_n), {\mathscr D}(M_l(R_n,I_n,J_n)), {\mathscr D}(R_n/J_n))$ in Theorem 1.2(1)). In a similar way, we show the statements on $B_n$ by the recollement $({\mathscr D}(B_0), {\mathscr D}(B_{n+1}), {\mathscr D}(B_n))$ in Theorem 1.2(1).

(2) Derived equivalent algebras have isomorphic algebraic $K$-groups (see [DS04]). By Lemma 5.9(a) and the proof of Theorem 1.2(1), we have

\begin{align*} K_*(A_{n+1})\simeq K_*(M_l(R_n,I_n,J_n))\simeq K_*(R_n/I_n)\oplus K_*(R_n/J_n)\simeq 2K_*(A_n) \end{align*}

and

\begin{align*} K_*(B_{n+1})\simeq K_*(M_l(S_n,K_n,L_n))\simeq K_*(S_n/K_n)\oplus K_*(S_n/L_n)\simeq K_*(B_0)\oplus K_*(B_n). \end{align*}

Starting with $A_1=A=B_1$, we can show the isomorphisms in $(2)$ by induction.

(3) By Lemma 5.9(b) and Theorem 1.2(2), $K_*(R_n)\simeq K_*(R_{n-1})\oplus K_*(A_n)$ and $K_*(S_n)\simeq K_*(S_{n-1})\oplus K_*(B_0)$ for $n\geq 1$. Together with $(2)$, we can show the isomorphisms in $(3)$ by induction.

Remark 5.11 Without assuming ${\rm domdim}(A)=\infty$, the isomorphisms in Corollary 5.10(3) still hold for $*=0$. This follows from Corollary 5.10(2) and the fact that if $R$ is a finite-dimensional algebra over a field and $f^2=f\in R$, then $K_0(R)\simeq K_0(fRf)\oplus K_0(R/RfR)$. Thus, $\#(R_n)= \#(\Lambda )+(2^n-1)\,\#(A)$ and $\#(S_n)=\#(\Lambda ) + n\; \#(B_0)$.

As a consequence of Theorem 1.2, we obtain bounds for the stratified dimensions and ratios of iterated mirror-reflective algebras of gendo-symmetric algebras which are not symmetric. This provides a new approach to attacking Tachikawa's second conjecture.

Corollary 5.12 Let $n$ be a positive integer, and let $(A,e)$ be a gendo-symmetric algebra with ${\rm domdim}(A)=\infty$. If $A$ is not symmetric, then the following statements hold.

1. (1) $2^n-1\leq {\rm stdim}(eAe)+(2^n-1)({\rm stdim}(A)+1)\leq {\rm stdim}(R_n)\leq \#(eAe)+(2^n-1)\,\#(A)-1$ and

   \begin{align*} n\leq {\rm stdim}(eAe)+n({\rm stdim}(B_0)+1) \leq {\rm stdim}(S_n)\leq \#(eAe)+ n\,\#(B_0)-1. \end{align*}

2. (2) ${{\rm stdim}(A)+1}{\#(A)}\leq \varliminf _{n\to \infty } {\rm sr}(R_n)\leq 1$ and

   \begin{align*} {{\rm stdim}(B_0)+1}{\#(B_0)}\leq \mathop{\varliminf}_{n\to\infty}{\rm sr}(S_n)\leq 1. \end{align*}
   In particular, if $B_0$ is local, then $\lim _{n\to \infty }{\rm sr}(S_n)=1$, where $\varliminf$ means the limit inferior.

Proof. (1) By Theorem 1.2(2) and Proposition 4.9(3), ${\rm stdim}(R_n)\geq {\rm stdim}(R_{n-1})+{\rm stdim}(A_n)+1$ and ${\rm stdim}(S_n)\geq {\rm stdim}(S_{n-1})+{\rm stdim}(B_0)+1$. Similarly, by Remark 5.8 and Proposition 4.9(3), we have ${\rm stdim}(A_{n+1})\geq 2\, {\rm stdim}(A_n)+1$, that is, ${\rm stdim}(A_{n+1})+1\geq 2({\rm stdim}(A_n)+1)$. Moreover, by Proposition 4.9(1), ${\rm stdim}(R_n)\leq \#(R_n)-1$ and ${\rm stdim}(S_n)\leq \#(S_n)-1$. Combining these inequalities with Remark 5.11, we get $(1)$ by induction.

(2) This follows from $(1)$ and Remark 5.11.

Finally, we state the promised connections between ${\rm (TC2)}$ and stratified dimensions of algebras in the following theorem, which is the combination of Theorems 1.1(1) and 1.3.

Theorem 5.13 Let $k$ be a field. The following statements are equivalent.

1. (1) $({TC2})$ holds for all symmetric $k$-algebras.

2. (2) No indecomposable symmetric $k$-algebra has a stratifying ideal apart from itself and $0$.

3. (3) The supremum of stratified ratios of all indecomposable symmetric $k$-algebras is less than $1$.

Proof. $(1)\Rightarrow (2)$ This is shown in Introduction.

$(2)\Rightarrow (3)$ An algebra $S$ has no stratifying ideal apart from itself and $0$ if and only if ${\rm stdim}(S)=0$ if and only if ${\rm sr}(S)=0$. Thus, $(3)$ follows.

$(3)\Rightarrow (1)$ Suppose that (TC2) does not hold for an indecomposable symmetric algebra $S$ over $k$. Then there exists an indecomposable, nonprojective self-orthogonal $S$-module $M$. Then $A:={\rm End}_S(S\oplus M)$ is a gendo-symmetric, but not a symmetric algebra. Let $S_n$ be the $n$th reduced mirror symmetric algebra of $A$ for $n\geq 1$. Then $S_n$ is symmetric by Proposition 5.3(1). As $M$ is indecomposable, ${\rm End}_S(M)$ is local. Since $M$ contains no nonzero projective direct summands, $S_1$ is indecomposable by Proposition 5.3(3). Further, by the proof of Theorem 1.2(1), ${\rm End}_S(M)\simeq (1_{B_n}-f_n)B_n(1_{B_n}-f_n)$ as algebras for any $n\geq 1$. Combining this fact with Proposition 5.3(2), we show that $S_n$ is indecomposable by induction. Since $M$ is self-orthogonal, we see ${\rm domdim}(A)=\infty$ by [Mul68, Lemma 3]. It follows from Corollary 5.12(2) that $\lim _{n\to \infty }{\rm sr}(S_n)=1$. Thus, the supremum in $(3)$ must be $1$, a contradiction to the assumption (3). This shows that $(3)$ implies $(1)$.