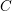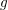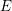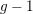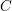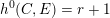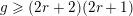Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Verra, Alessandro
2018.
Edge and Fano on nets of quadrics.
European Journal of Mathematics,
Vol. 4,
Issue. 3,
p.
1264.
Hitching, George H.
2020.
A Riemann–Kempf singularity theorem for higher rank Brill–Noether loci.
Bulletin of the London Mathematical Society,
Vol. 52,
Issue. 4,
p.
620.
Hitching, George H.
Hoff, Michael
and
Newstead, Peter E.
2021.
Nonemptiness and smoothness of twisted Brill–Noether loci.
Annali di Matematica Pura ed Applicata (1923 -),
Vol. 200,
Issue. 2,
p.
685.
BOLOGNESI, MICHELE
and
VARGAS, N. F.
2022.
THE HYPERELLIPTIC THETA MAP AND OSCULATING PROJECTIONS.
Nagoya Mathematical Journal,
Vol. 245,
Issue. ,
p.
206.